Lattice Boltzmann method for Casimir invariant of two-dimensional turbulence*

Yu-xian XIA （夏玉显），Yue-hong QIAN （钱跃竑）

Shanghai Institute of Applied Mathematics and Mechanics，Shanghai University，Shanghai 200072，China，E-mail:xiayuxian2008.com@163.com

Lattice Boltzmann method for Casimir invariant of two-dimensional turbulence*

Yu-xian XIA （夏玉显），Yue-hong QIAN （钱跃竑）

Shanghai Institute of Applied Mathematics and Mechanics，Shanghai University，Shanghai 200072，China，E-mail:xiayuxian2008.com@163.com

The Casimir invariants of the 2-D turbulence are investigated by the lattice Boltzmann method.A coarse-graining approach is used，that allows to resolve the flux of the Casimir invariant in scale and in space.It is found that the flux of the enstrophy cascades to small scales and the direction cascade of the energy flux is upscaled.Moveover，the probability distribution function （PDF） of the enstrophy flux gives a clear evidence that the enstrophy cascades to smaller scales.Finally，the behavior of the cascade of the high-order Casimir invariants Znis discussed.The flux of the fourth-order Casimir invariant Z4cascades to small scales.The flux of Znhas a logarithmic relationship with the scale，that is，

2-D turbulence，Casimir invariants，lattice Boltzmann method

Introduction

It is commonly believed that the simultaneous conservation of the energy and the enstrophy by the advection term of the forced 2-D Navier-Stokes equations gives rise to a dual turbulence cascade when the Reynolds number tends to infinity［1-3］.Under statistically stationary conditions，when the turbulent flow is sustained by an external forcing acting in a typical force scale lf，a double cascade develops.According to the Kraichnan theory，at a large scale，i.e.，when the wave numbersk≪kf～l-f1，the energy spectrum assumes the formE（ k）≈ε2/3k-5/3while in small scales，k≫kf，the prediction is E（ k）≈η2/3k-3，witha possible logarithmic correction［1］.Here η=k2ε.ε and η are，respectively，the energy and the enstrophy injection rates.

In addition to conserving the energy and the enstrophy，the nonlinear terms of the 2-D incompressible Navier-Stokes equation are well known to conserve the global integral of any continuously differentiable function of the scalar vorticity field，which are known as the Casimir invariants.A fundamental question is whether these Casimir invariants also play an underlying role in the turbulence cascade，in addition to the rugged quadratic invariants （the enstrophy）.Whether they cascade to large or small scales is an open question.Polyakov' minimal conformal field theory model suggests that the higher-order Casimir invariants cascade to large scales［4］，while Eyink［5］predicted that they might instead cascade to small scales.Bowman［6］pointed out that the fourth power of the vorticity cascades to small scales by using the wellresolved implicitly dealiased pseudospectral simulations.Meanwhile，this study raises the question of whether the Kraichnan theory of the unbounded 2-D turbulence，based solely on the uniform flux of the energy in large scales and that of the enstrophy in small scales，needs to be re-examined to account for a direct cascade of the Casimir invariants to smaller scales.

A better understanding of the physical mechanism on the basis of the cascades can be obtained by looking at the distribution of the fluxes of the Casimir invariant in scales.Here the key analysis method we use is a “coarse-graining” or “filtering” approach for analyzing the scale interactions in complex flows.Eyink［7］developed the formalism mathematically to analyze the fundamental physics of the scale coupling in turbulence，which was laterly applied to numerical and experimental studies of flows of 2-D turbulence［8-12］.For any field a（ x），a “coarse-graining” or“filtering” field，which contains modes at a lengthscale＞l，is defined as

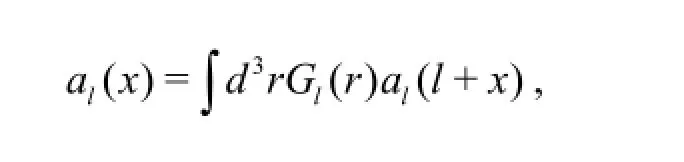
where Gl（ r）is a normalized convolution kernel.It is well known that the lattice Boltzmann method （LBM）is valid in the investigations of 2-D turbulence［3，13，14］.In this paper，this “filtering” approach is used to investigate the flux of the Casimir invariant in the frame of the LBM.

1.Preliminaries

1.1 The flux of Casimir invariants

The balance equations governing the local conservation of the vorticity invariants are expressed in space and in scale.Due to the viscous effect，the high order Casimir invariants are generally not in conservation.However，it is verified that the viscosity has no influence on the definition of the flux of high order Casimir invariants.To introduce the concepts in the simple context，we discuss first the free evolution，i.e.，the equations without any external forcing.Thus，our starting point is the 2-D Euler equations in the “vorticity formulation”.

That is，we consider the large-scale vorticity defined by convolutionand the large-scale velocity defined by，where Glis taken to be the Gaussian filter.If the filter is convoluted with the equation of motion，Eq.（1），an equation for the largescale vorticity field is obtained

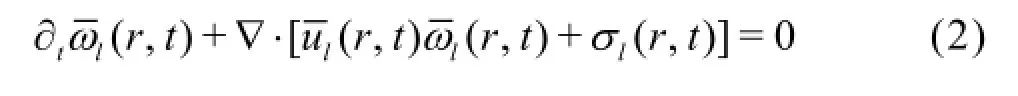
where σlis the space transport of the vorticity due to the eliminated small-scale turbulence.From Eq.（2），a balance equation is derived for the local densityhl（ r，t）=

where Kl（ r，t）represents the space transport of the large-scale enstrophy，

In Eq.（3），we see that in order forto have a net positive value，the turbulence vorticity transport σl（r，t）should tend to be antiparallel to the large-scale vorticity gradientThe required statistical anticorrelation between σl（r，t）and（r，t）is an alignment property characteristic of the enstrophy cascade.It is analogous to the much-studied alignment of the stress tensorτidue to small scales and the large-scale strain，which underlies the energy cascade to small scales in 3-D.

An identical analysis can be made of the balance for the local densitiesof the contribution to the Casimir invariants Znin the largescale modesBy a similar calculation as before，it follows that

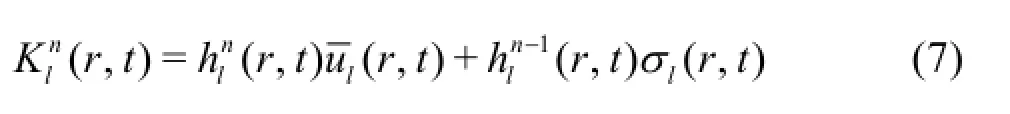
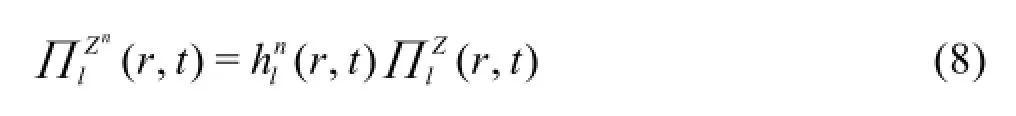
It is of some interest that it is simply proportional to the enstrophy flux itself，when n＞2.

1.2 lattice Boltzmann method （LBM）

The Navier-Stokes equation for the fluid flows can be simulated by the LBM in a simple and efficient way［13，15-19］.The LBM has its roots in the kinetic theory，and the general idea behind this scheme is to compute a probability distribution function fi（ r，t），where

Table 1 Parameters of the simulations

fi（ r，t）is the population of the particles，withi representing the fluid element with a corresponding velocity along the directioniat the positioniand the timex，as they stream and collide.The statistical behavior of the distribution of the particle population delineates that of the dynamics of the fluid flow.For 2-D incompressible fluid flows，the popular D2Q9 model［13］is used to simulate various fluid flow problems，whose evolution equation for fi（ r，t）can be described by

where ciis the discrete particle velocity，τdenotes the relaxation time，and the local equilibrium distribution is as follows

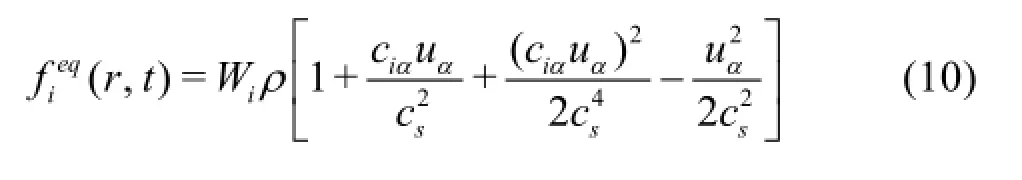
where Wiis the lattice weight，αis a Cartesian coordinate （with implied summation convention for repeated indices） andis the speed of sound.Fiis the external force term andis the friction term.The local macroscopic density and the velocity field are then obtained by

By using the Chapman-Enskog expansion，the Navier-Stokes equations can be derived to the second order of the Knudsen number at a long wavelength and long time limits，

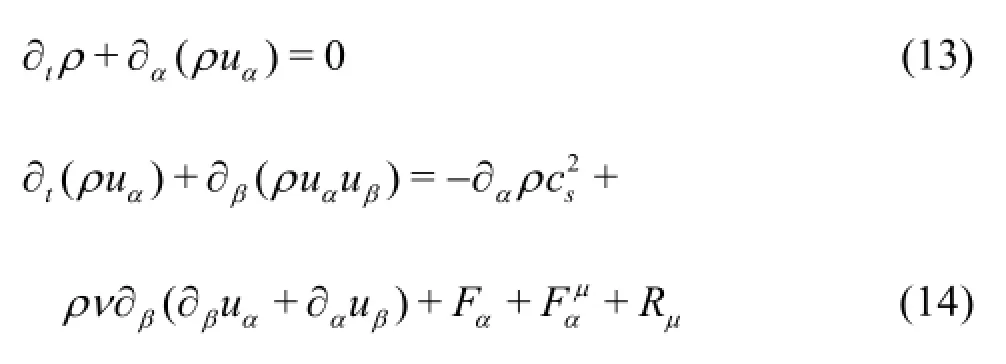
where Fαis the external force of the system，is the friction force，andνis the viscosity coefficient.The relationship between the external force term Fiin Eq.（9）.and the external force Fαof the system in Eq.（14）.is described by

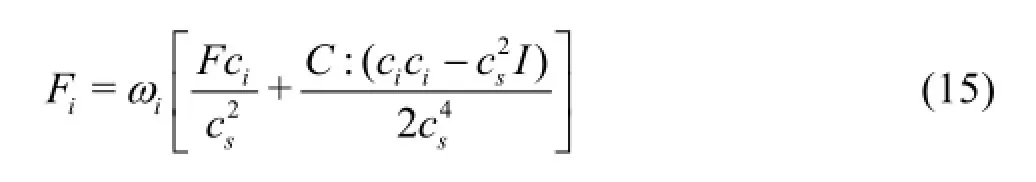
where C=［1- 1/2τ（uF-Fu）］.The relationship between the friction force termand the friction forceis the sam e as Eq.（15）.In order to obtain the steady state，the linear friction µuis necessary to avoid a energy condensation in a large scale.The additional term Rµin the momentum equation of Eq.（14）.is due to the presence of an external force.

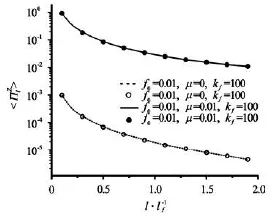
Fig.1 The scale behaviors of the enstrophy flux in two cases of LBM external force model.Here the external force is band-limited 0.9lf＜l＜1.1lf.Solid curve and dot line represent the Ladd and Verberg force model，dot curve and circle are LGA force model

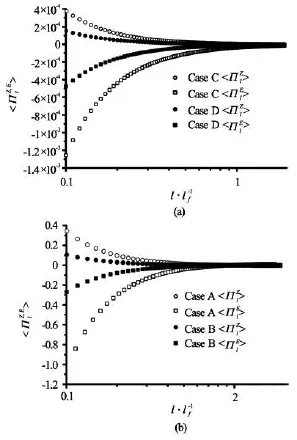
Fig.2 The average enstrophy flux and energy flux as a function of length scale l/ lf.Hollow circle represents enstrophy flux in Case A，hollow square represents energy flux in Case A，solid circle represents enstrophy flux in Case B，solid square represents energy flux in Case B.Hollow circle represents enstrophy flux in Case C，hollow square represents energy flux in Case C，solid circle represents enstrophy flux in Case D，solid square represents energy flux in Case B

In the case of the Ladd and Verberg external forced model，In fact，if the external forceFαis a constant with time，Eq.（14） will be the correct hydrodynamic equation［3］.It is found in Fig.1 that the artificial termRµdoes not affect the cascade and statistical behaviors of the 2-D turbulence，so the more detail about Rµwill not be discussed here.The detailed information of the external forcing is given in Table 1.The external force scale Reynolds number of the 2-D turbulence Ref～（kmax/kf）2（kmax=N /2）.The initial energy spectrum E（ k）=（k/4.68）4exp［2.0（k/4.68）2］will not lead to the significant inverse energy cascade of a short duration simulation.The 2D turbulence is investigated by means of a standard LBM parallel code on a double periodic square domain with the sidesLx=Ly=2π.

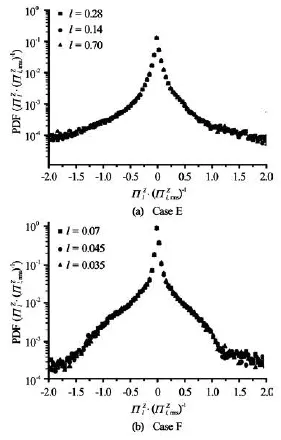
Fig.3 Normalized probability distribution functions for the scale-to-scale enstrophy flux

2.Numerical results

The space average of the coarse-grained enstrophy budget as a function of the scale l is calculated.Obviously，the average enstrophy fluxes in different external scaleskf，shown in Fig.2，cascade to small scales.The enstrophy flux falls off in all length scales.The fall in the enstrophy transfer in all scales is due to the effect of the linear frictional force on the full field of the 2-D turbulence.

It is interesting to measure the energy transfer in the 2-D turbulence，which may reflect the behavior observed more generally in systems with a quasi-2-D character［20，21］.In Fig.2，the mean energy transfers for Cases A，B，C，D are negative revealing that the energy cascades to the upscale despite the expected lack of a constant energy flux.It also increases and goes to zero in the length scales smaller than the injection scale lf.The behavior of the energy flux issomewhat dependent on the form of the full-band external force.It is verified that the more energy is injected in a smaller scale.So the more energy is transferred to a larger scale from a smaller scale.Figure 2 shows the double cascade of the 2-D turbulence.

The PDFs，shown in Fig.3，are normalized by their respective rms fluctuations.These PDFsin Case E and Case F where the linear friction coefficientµis equal to zero are asymmetric and positively skewed.The PDF has a positive mean，indicating that there is a net transfer of the enstrophy to a smaller scale.These PDFs recorded for different separations lare strongly non-Gaussian，with long tails for large values of the enstrophy flux.The shapes of the PDFs do vary with the scale in the large fluctuation event，thus showing the nature of the intermittency in the enstrophy cascade range corresponding to our result［3］that the intermittency exists in the direct inertial range due to the statistical feature in the velocity field.

Fig.4 The average enstrophy flux and energy flux as a function of length scale l/ lfwhen l＞0.9lfin Case D.Hollow circle represents enstrophy flux，solid circle represents energy flux

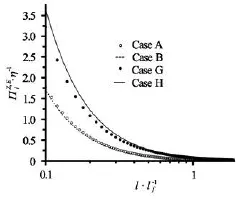
Fig.5 The effect of finite resolution on the enstrophy flux as a function of length scale l/ lf.Hollow circle represents Case A，dot curve represents Case B，solid circle represents Case G，and solid curve represents Case H

It is important to explore whether the external force scale kmax/kfaffects the cascade of the Casimir invariants.The enstrophy flux in Case D withkmax/ kfequal to 3.41，described in Fig.4，becomes negative in the injection scalelf.The value of kmax/kfin Case D is small so as to see the finite resolution effect on the enstrophy flux.This is not a surprise because the extent of the direct cascade is simply proportional to kmax/kfWhen the values of kmax/kfin Case A and Case C are larger than that in Case D where kmax/kfis equal to 10.24，the sign of the enstrophy flux does not change in all length scales.The enstrophy is really positive in all length scales in the 2-D turbulence forced by the full-band force.From Fig.5，the direction of the enstrophy flux in Cases A and B is consistent with that in Cases G and H where kmax/kfis equal to 20.48.Obviously，the external force scale does have an influence on the Casimir cascade.In order to have a wider range of the inertial range and avoid the finite resolution effect，the condition that kmax/kf≥10.24should be satisfied to investigate the higher order Casimir invariant of the 2-D turbulence.

Fig.6 The average fourth-order Casimir invariant flux as a function o f length scale l/ lfin Case G and Case H，in Case G，ζ4=2.15±0.1 in Case H.Solid circle represents Case G，hollow circle represents Case H

Next，the cascade direction of the higher order Casimir invariant Zn（n＞2）is estimated.The globally integrated invariantZ3appears to slosh back and forth between the large and small scales.In retrospect，this should be expected sinceω3is not a sign-definite quantity.So，we mainly focus on the determination of a sign-definite quantity like the fourth-order Casimir invariant Z4.Fig.6 displays the space behaviors of Z4.The flux of the fourth-order Casimir invariantcascades to small scales.It is seen in Fig.6 that the flux ofZ4has the logarithmic relationship withthe scale，that is，.In Case G，ζ4=2.15± 0.1 in all length scales.ζ4=2.15±0.1in Case H.Obviously，the friction force does not break up the logarithmic behaviors of the fourth-order Casimir invariant.Figure 7 shows the nonlinear relationship betweenζnand the order n（ n=2，4，6）in the enstrophy inertial range.It shows that the intermittency exists in the enstrophy cascade according to the statistical behaviors of higher-order Casimir invariants.

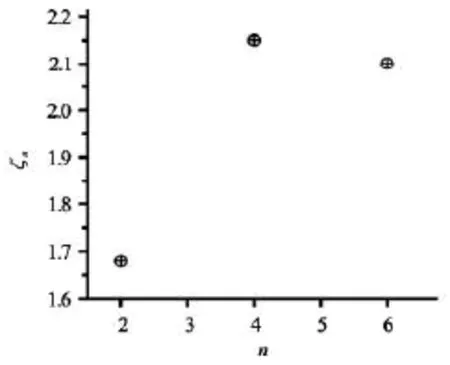
Fig.7 The relationship between Znand the order n（ n=2，4，6）in the enstrophy inertial range.ζ2=1.68±0.2，ζ4=2.15±0.1，ζ6=2.10

3.Conclusion

We have presented a statistical analysis of the 2-D turbulence and how to obtain a band-pass decomposition of the flux of Casimir invariants with a Gaussian filter.The mathematical form of the flux of Casimir invariants given in this paper is easy to be used to reveal the cascade behaviors of Casimir invariants.It is verified that the flux of the fourth-order Casimir invariant Z4cascades to small scales.And also，this flux has a uniform logarithmic relationship with the scale.This logarithmic relationship raises the question of whether the Kraichnan theory of the unbounded 2-D turbulence，based solely on the uniform flux of the energy to large scales and that of the enstrophy to small scales，needs to be revisited to account for a direct cascade of Casimir invariants to small scales.In future，we will focus on this issue.

［1］BOFFETTA G.，ECKE R.E.Two dimensional turbulence［J］.Annual Review of Fluid Mechanics，2012，44（3）:427-451.

［2］THUBURN J.，KENT J.and WOO D.N.Cascades，backscatter and conservation in numerical models of twodimensional turbulence［J］.Quarterly Journal of the Royal Meteorological Society，2013，140（679）:626-638.

［3］XIA Y.X.，QIAN Y.H.Lattice Boltzmann simulation for forced two-dimensional turbulence［J］.Physical Review E，2014，90（2）:023004.

［4］POLYAKOV A.M.The theory of turbulence in two dimensions［J］.Nuclear Physics B，1993，396（2-3）:367-385.

［5］EYINK G.L.Exact results on stationary turbulence in 2D:Consequences of vorticity conservation［J］.Physica D，1996，91（1-2）:97-195.

［6］BOWMAN J.C.Casimir cascades in two-dimensional turbulence［J］.Journal of Fluid Mechanics，2013，729:364-376.

［7］EYINK G.Local energy flux and the refined similarity hypothesis［J］.Journal of Statistical Physics，1995，78（1）:335-351.

［8］EYINK G.Multi-scale gradient expansion of turbulence stress tensor［J］.Journal of Fluid Mechanics，2006，549:159-190.

［9］CHEN S.Y.，ECKE R.E.and EYINK G.L.et al.Physical mechanism of the two-dimensional enstrophy cascade［J］.Physical Review Letters，2003，91（21）:214501.

［10］CHEN S.Y.，ECKE R.E.and EYINK G.L.et al.Physical mechanism of the two-dimensional inverse energy cascade［J］.Physical Review Letters，2006，96（8）:084502.

［11］RIVERA M.K.，DANIEL W.B.and CHEN S.Y.et al.Energy and enstrophy transfer in decaying two-dimensional turbulence［J］.Physical Review Letters，2003，90（10）:104502.

［12］RIVERA M.K.，ALUIE H.and ECKE R.E.The direct enstrophy cascade of two-dimensional soap film flows［J］.Physics of Fluids，2013，26（5）:499-502.

［13］XU H.，QIAN Y.H.and TAO W.Q.Revisiting twodimensional turbulence by lattice Boltzmann method［J］.Progress in Computational Fluid Dynamics，2009，9（3）:133-140.

［14］BENZI R.，SUCCI S.Two-dimensional turbulence with the lattice Boltzmann equation［J］.Journal of Physics A Mathematical and General，1990，23（1）:L1-L5.

［15］QIAN Y.H.，DʹHUMIÈRES D.and LALLEMAND P.Lattice BGK models for Navier-Stokes equation［J］.Europhysics Letters，1992，17（6）:479-484.

［16］QIAN Y.H.Simulating thermohydrodynamics with lattice BGK models［J］.Journal of Computational Physics，1993，8（3）:231-242.

［17］BENZI R.，SUCCI S.and VERGASSOLA M.The lattice boltzmann equation:Theory and applications［J］.Physics Reports，1992，222（3）:145-197.

［18］AIDUN C.K.，CLAUSEN J.R.Lattice-Boltzmann method for complex flows［J］.Annual Review of Fluid Mechanics，2010，42（1）:439-472.

［19］DIAO Wei，Cheng Yong-guang and ZHANG Chun-ze et al.Three-dimensional prediction of reservoir water temperature by the lattice Boltzmann method:Validation［J］.Journal of Hydrodynamics，2015，27（2）:248-256.

［20］BOFFETTA G.Energy and enstrophy fluxes in the double cascade of two- dimensional turbulence［J］.Journal of Fluid Mechanics，2007，589:253-260.

［21］BOFFETTA G.，MUSACCHIO S.Evidence for the double cascade scenario in two-dimensional turbulence［J］.Physical Review E，Statistical，Nonlinear，and Soft Matter Physics，2010，82（2）:016307.

10.1016/S1001-6058（16）60634-0

（Received July 10，2014，Revised August 11，2015）

* Project supported by the National Natural Science Foundation of China （Grant No.91441104），the Ministry of Education in China via project （Grant No.IRT0844） and the Shanghai Science and Technology Commission Project of leading Scientists and Excellent Academic Leaders （Grant No.11XD1402300）.

Biography:Yu-xian XIA （1982-），Male，Ph.D.Candidate

Yue-hong QIAN，E-mail:qian@shu.edu.cn

2016，28（2）:319-324