Numerical simulation of self-similar thermal convection from a spinning cone in anisotropic porous medium*
O.Anwar BÉG,M.J.UDDIN,T.BÉG,R.Reddy GORLA
1.Spray Research Group,Petroleum and Gas Engineering Division,Room G77,Newton Building,School of Computing,Science and Engineering (CSE),University of Salford,M54WT,UK,E-mail:gortoab@gmail.com
2.Department of Mathematics,American International University-Bangladesh,Dhaka,Bangladesh
3.Engineering Mechanics Associates,Dickenson Road,Manchester,M16,England,UK
4.Department Mechanical Engineering,Cleveland State University,Cleveland,Ohio,USA
Numerical simulation of self-similar thermal convection from a spinning cone in anisotropic porous medium*
O.Anwar BÉG1,M.J.UDDIN2,T.BÉG3,R.Reddy GORLA4
1.Spray Research Group,Petroleum and Gas Engineering Division,Room G77,Newton Building,School of Computing,Science and Engineering (CSE),University of Salford,M54WT,UK,E-mail:gortoab@gmail.com
2.Department of Mathematics,American International University-Bangladesh,Dhaka,Bangladesh
3.Engineering Mechanics Associates,Dickenson Road,Manchester,M16,England,UK
4.Department Mechanical Engineering,Cleveland State University,Cleveland,Ohio,USA
Self-similar steady natural convection thermal boundary layer flow from a rotating vertical cone to anisotropic Darcian porous medium is investigated theoretically and numerically.The transformed non-dimensional two-point boundary value problem is reduced to a system of coupled,highly nonlinear ordinary differential equations,which are solved subject to robust surface and free stream boundary conditions with the MAPLE 17 numerical quadrature software.Validation with earlier non-rotating studies is included,and also further verification of rotating solutions is achieved with a variational finite element method (FEM).The rotational(spin) parameter emerges as an inverse function of the Grashof number.The influence of this parameter,primary Darcy number,secondary Darcy number and Prandtl number on tangential velocity and swirl velocity,temperature and heat transfer rate are studied in detail.It is found that the dimensionless tangential velocity increases whilst the dimensionless swirl velocity and temperature decrease with the swirl Darcy number,tangential Darcy number and the rotational parameters.The model finds applications in chemical engineering filtration processing,liquid coating and spinning cone distillation columns.
self-similarity,spinning cone,finite element method (FEM),anisotropic porous medium,heat transfer,MAPLE,FEM
Introduction
Rotational thermal convection flows on bodies of axisymmetric geometry have been studied for a number of decades by engineers and mathematicians,initially due to interest in the aerospace sciences.The Coriolis forces experienced with rotation generated by the centrifugal field cause fluid to be impelled along the curved surface and substantially enhance heat transfer rates.Since the seminal review by Grief[1]interest in external rotating heat transfer has continued to flourish.These flows abound in chemical engineering processing where they arise in spinning cone distillation columns and centrifugal film evaporators[2],aeration devices and atomizers[3].Many excellent experimental,theoretical and computational studies have been communicated to elucidate the interaction of viscous,rotational and other body force effects in such flows.Chamkha and Rashad[4]investigated unsteady heat and mass transfer due to MHD mixed convection flow past rotating vertical cone with chemical reaction and soret and dufour effects.Osalusi et al.[5]examined the effect of viscous dissipation and Joule heating on unsteady MHD flow on a rotating cone in rotating fluid.Narayana et al.[6]studied free magnetohydrodynamic flow and convection from a vertical spinning cone with cross-diffusion effects.Anilkumar and Roy[7]employed Bellman-Kalaba quasi-linearization and an implicit finite difference scheme to study transient heat and mass transfer from a rotating cone,computing Sherwood numbers for a range of rotation parameters,and observing that self-similar solutions are only admitted when both the free stream angular velocity and cone rotational velocity vary as linear inverse functions of time.Raju et al.[8]studied thermophoret-ic effect on double diffusive convective flow of a chemicallyreacting fluid over a rotating cone in porous.Further studies of rotational thermal convection from a spinning body have been presented by Ece[9]for steady magnetic convection.
The above studies have considered only pure fluid regimes external to the rotating body.In numerous energy resources areas,however the external medium is often porous i.e.,comprises a permeable material.As such extra body forces must be incorporated into the analysis to account for linear porous resistance at lower Reynolds numbers.Porous media offer excellent properties for flow control and filtration.Most porous heat transfer flow studies have used the isotropic Darcy law[10,11],which assumes that permeability in all directions is the same.A more general case is that of anisotropic porous media[12]which incorporates a variation in the permeability depending on the direction.This better characterizes many synthetic and geological materials.Anisotropy is normally results of preferential orientation or asymmetric geometry of porous matrix or fibers.It occurs in many industrial system and nature.Besides,anisotropy can also be a characteristic of artificial porous materials such as pelleting used in chemical engineering process,fiber material used in insulating purpose and packed beds used in the storage of heat energy.
In the present study we shall therefore examine the thermal convection from a rotating cone to anisotropic Darcian porous media.This regime is relevant to filtration chemical engineering coating applications.A MAPLE numerical solution[13]to the transformed ordinary differential equations is obtained.The computations are validated with purely fluid (infinite permeability) solutions in the literature and also with a variational finite element code[14]based on linear elements.The present study presents a comprehensive examination of anisotropic permeability effects on rotating cone convection in porous media and to the authors' knowledge has not appeared in the literature thus far.
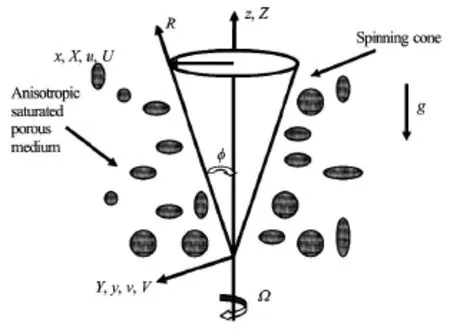
Fig.1 Physical model for convection from a rotating cone in an anisotropic porous regime
1.Mathematical rotating flow model
The physical model is depicted in Fig.1.We consider steady-state,laminar,incompressible,axisymmetric,free convection boundary layer flow along a rotating cone embedded in an anisotropic saturated porous regime.
Tortuosity and thermal dispersion effects in the porous medium are neglected.The Darcy model is employed[15].The cone surface is isothermal.Rotation is sufficiently slow to ignored compressibility effects.The X direction is parallel to the cone slant surface,the Y direction normal to this and θ designates the angle in a plane perpendicular to the vertical symmetry axis.The cone may represent for example a chemical engineering mixing device.The governing equations for the flow regime can be posed as follows with reference to an (X ,Y,θ) coordinate system:
Mass

Momentum

Momentum

Energy
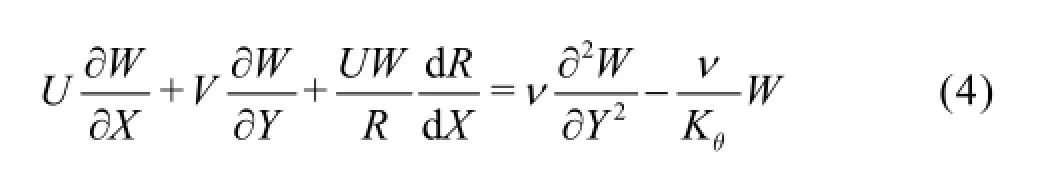
The Boussinesq approximation has been used so that buoyancy effects only appear in the X-direction momentum Eq.(2),which is coupled to the energy equation,constituting a free convection regime.Using separate permeabilities in the X and θ directions(due to anisotropy),two porous media drag force terms are present,one in each of Eqs.(2) and (3) i.e.,the primary and secondary Darcian impedance.Viscous dissipation and cross-diffusion (Soret/Dufour) effects are ignored.The corresponding boundary conditions at the surface and far from the cone are:

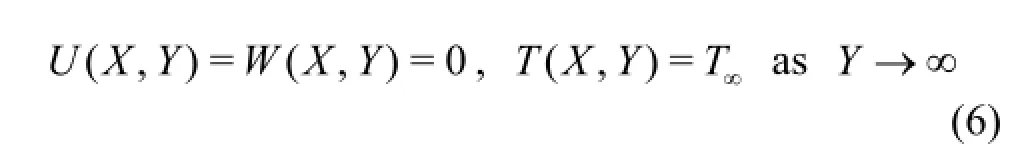
where the following notation applies:X is the coordinate parallel to cone surface,Y is the coordinate normal to cone surface,θis the angular coordinate,R is the radial coordinate,ris the local radius of the cone,Uis the velocity component inX direction,V is the velocity component inY direction,Wis the velocity component in θ direction,Tis the fluid temperature,Twis the cone surface temperature,T∞is the free stream temperature,U*is the reference velocity,gis the gravitational acceleration,νis the kinematic viscosity of fluid,ρis the density of fluid,KXis the permeability inX direction,Kθis the permeability in θ direction,α is the thermal diffusivity of the fluid,β is the coefficient of thermal expansion of the fluid,Ω is the rotational velocity of the cone (spin velocity about symmetry axis),φ is the semi-vertex angle of cone.The boundary layer Eqs.(1)to (4) are highly coupled,parabolic and nonlinear.An analytical solution is clearly intractable and in order to obtain a robust solution,we next non-dimensionalize the model.Proceeding with the analysis,we introduce the following transformations:

The transport equations are thereby reduced to the following dimensionless equations:
Mass

Tangential momentum
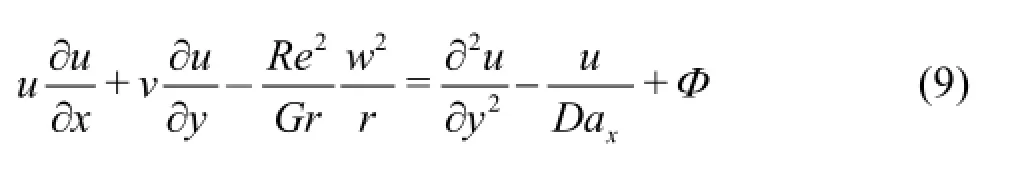
Swirl momentum

Thermal energy (heat)

The boundary conditions are also transformed into:

In Eqs.(8)-(13),the following notation applies:F is the similarity boundary layer stream function,G is the similarity boundary layer rotational (swirl) velocity,His the similarity boundary layer temperature function,xis the trans formed X coordinate,yis the trans formed Y coordinate,r is the transformed local cone radius,u is the trans formed X velocity,vis the trans formed Y velocity,w is the trans formed θ velocity,D a is the tangential Darcy number,Daθ(swirl Darcy number),Pr is the Prandtl number,Φ is the non-dimensional temperature function,Gr is the modified Grash of number,Re is the rotational Reynolds number,L-reference scale length.The nondimensional Eqs.(9) to (12) can be further simplified by employing appropriate similarity transformations.We first define a dimensional stream function,ψ,following Ece[9]:

The boundary layer variables are now re-scaled as follows,with r=xsinθ:

Introducing these relations into Eqs.(8)-(13),generates the following system of “self-similar “ordinary differential equations:
Tangential momentum
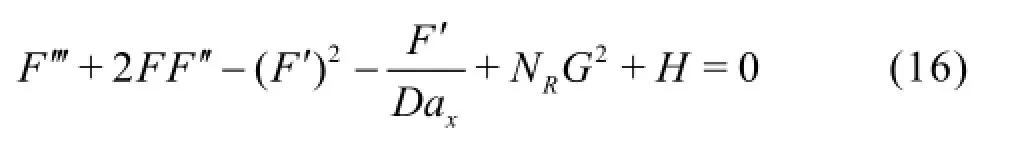
Swirl momentum
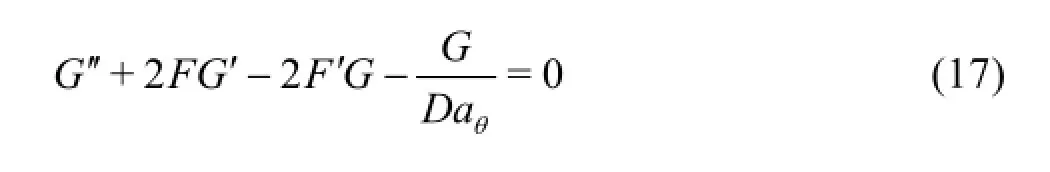
Energy

whereF is the boundary-layer stream function,G is the boundary-layer rotational (swirl) velocity,H is the boundary-layer temperature,DaxandDaθdenote the x -direction and θ-direction Darcy numbers,and NR=(R esinj)2/Gris the rotational (spin) parameter.We note that for the purely fluid case,Dax(tangential Darcy number)→∞and Daθ(swirl Darcy number)→∞since the permeability of the anisotropic regime becomes infinite.For the case of an isotropic porous medium,Dax=Daθ.The self-similar momentum Eqs.(16) and (17) then reduce to exactly the non-magnetic case of the generalized hydromagnetic equations solved by Ece[9]:

Equation (18) is identical also to the similarity heat transfer equation solved by Ece[10].The transformed boundary conditions are also identical to those solved by Ece[10]and for the current problem take the form:
F (0)=0,F′(0)=0,G (0)=1at the cone surface

F′(y)→0,G( y)→ (0),H( y)→0
2.Numerical solution by Maple 17
The self-similar nonlinear two-point boundary value problem is solved using MAPLE17[16]quadrature.This approach has been extensively implemented in a diverse array of nonlinear multi-physical flow problems in chemical and materials engineering sciences including annular magnetohydrodynamics[17],nano-structural mechanics[18],and nanofluid convection flows[19].A Runge-Kutta-Fehlberg fourth-fifth order numerical algorithm (RKF45) is employed,available in the symbolic computer software Maple 17.This utilizes a collocation method in which a finite-dimensional space of candidate solutions is selected(usually,polynomials up to a certain degree) and a number of points in the domain (called collocation points),and a solution selected which satisfies the given equation at the collocation points.The RFK45 algorithm is adaptive since it adjusts the quantity and location of grid points during iteration and thereby constrains the local error within acceptable specified bounds.In the current problem,the asymptotic boundary conditions given in Eq.(21) are replaced by a finite value in the range 15-20 depending on the parameters values.The choice of infinity must be selected judiciously to ensure that all numerical solutions approached to the asymptotic values correctly.The selection of sufficiently large value for infinity is imperative for maintaining desired accuracy in boundary layer flows,and is a common pitfall encountered in numerous studies.The stepping formulae used to solve Eqs.(16)-(18) under conditions (21) via fifth-fourth order Runge-Kutta-Fehlberg algorithms are given below[18]:
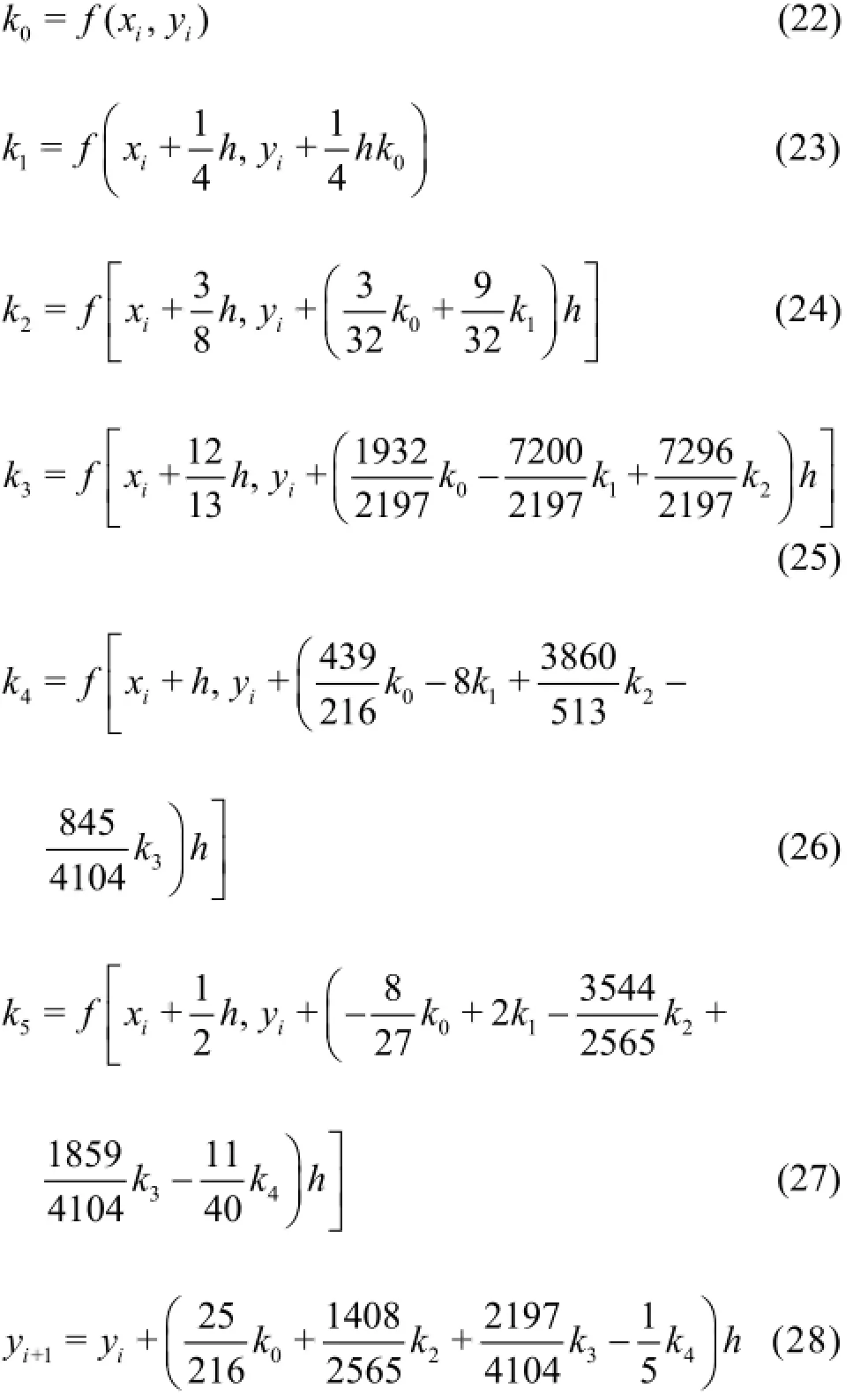

Table 1 Values of F′(0)for free-convection boundary-layer flow over a spinning cone with Dax→∞and Daθ→∞(purely fluid case)

Table 2 Values of -H′(0)for free-convection boundary-layer flow over a spinning cone with Dax→∞and Daθ→∞(purely fluid case)
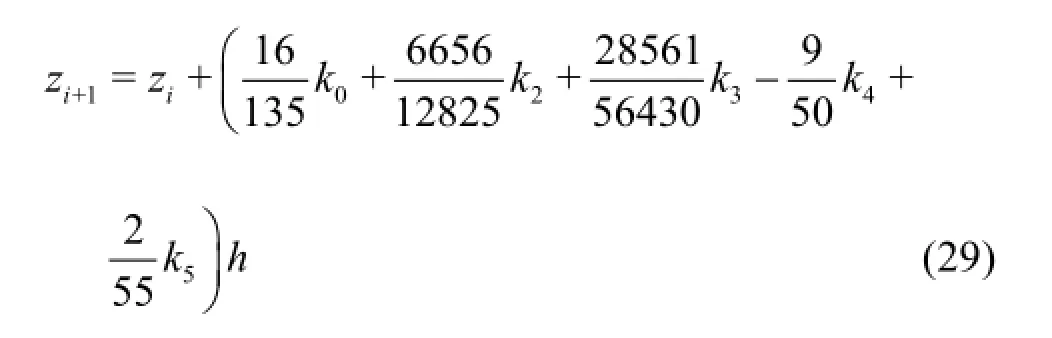
Here y denotes fourth-order Runge-Kutta phase and zis the fifth-order Runge-Kutta phase.An estimate of the error is achieved by subtracting the two values obtained.If the error exceeds a specified threshold,the results can be recalculated using a smaller step size.The approach to estimating the new step size is shown below

3.Galerkin finite element computations
The MAPLE numerical solutions have been validated using a Galerkin finite element method (FEM)[20].FEM also uses integration approximations,as with numerical quadrature.Applying the Galerkin finite element method to Eqs.(16) to (18) over the element(e)(yi≤y≤yk),we have[21]:
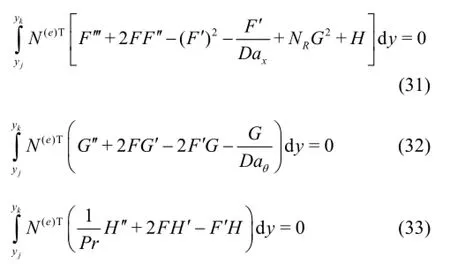
We postulate linear piecewise approximate solutions forF′,G,H with appropriate shape functions (interpolation functions).In order to prove the convergence and stability of the Galerkin finite element method,the Matlab program SPIN-FEM is executed with slightly modified values of the mesh distance in the y -direction i.e.,j,and no significant change is observed in the values of the velocity components.Mesh independence of solutions is therefore achieved with excellent stability and convergence[20].The boundary conditions (10) are easily specified in SPIN-FEM.The porous medium is discretized into a domain which is divided into smaller elements (sub-domains) of finite dimensions called “finite elements”.The collection of elements is called the finite-element mesh or grid.The element matrix,which is called a stiffness matrix,is constructed by using element interpolation functions.The algebraic equations so obtained are assembled by imposing the inter-element continuity conditions.This yields a large number of algebraic equations defining the global finite element model,which governs the whole domain.The essential and natural boundary conditions are imposed on the assembled equations.The assembled equations so obtained can be solved by any “matrix” numerical technique e.g.Householder's approach,LU Decomposition method etc..Further details are readily available in Ref.[21].Criteria for the selection of elements are also documented in the extensive review by Bég[22].The non-linear algebraic system of equations is solved iteratively.An accuracy of 10-7is used.A convergence criterion based on the relative difference between the current and previous iterations is employed.When these differences reach the desired accuracy,the solution is assumed to have converged and the iterative process is terminated.Two-point Gaussian quadrature is implemented for solving the integrations.The FEM algorithm has been executed in MATLAB running on an Octane SGI desktop workstation and takes 6 s-10 s on average.Excellent correlation is achieved with[9]as shown in Tables 1,2.
Both MAPLE and SPIN-FEM correlate very closely with the infinite permeability solutions of Ece[9].Confidence in the MAPLE code is therefore high.

Fig.2 Tangential velocity(F′)for various NRfor isotropic case(Pr=0.7,Dax=Daθ=1.0)
4.Maple computations,results and discussion
Extensive computations are conducted to simulate the variation of the tangential velocity(F′),swirl velocity (G)and temperature (H)with distance,y,into the boundary layer (transverse to the cone surface),5 thermophysical parameters are analyzed-Prandtl number(P r),magnetohydrodynamic number(N m),x -direction Darcy number (Dax),θ-direction Darcy number(Daθ)and rotational parameter (NR).The regime has high permeability in both the x -and θ-direction so that high values are prescribed for Daxand Daθ.i.e.,1.0,unless otherwise stated.Pris prescribed as 0.7 (accurate for air),NR=2.0(inertial rotation effects dominant buoyancy effects) unless otherwise indicated.All computations were conducted with MAPLE17 and are illustrated in Figs.2-17.Infinity is prescribed at 12 to ensure asymptotically smooth solutions are attained in the free stream.
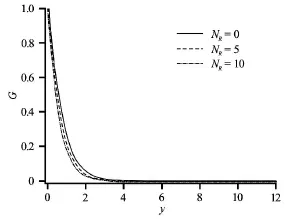
Fig.3 Swirl velocity(G)for various NR(Pr=0.7,Daθ= Dax=1.0)
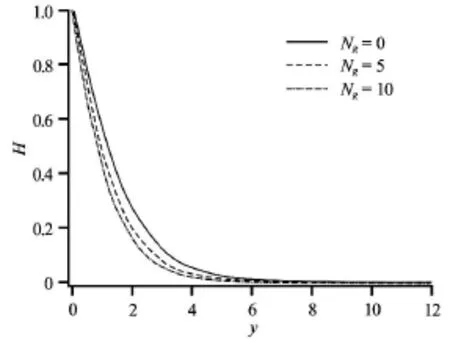
Fig.4 Temperature(H)for various NR(Pr=0.7,Daθ= Dax=1.0)
In Figs.2-5 the effects of rotational parameter,NR=(Resinφ)2/Gron tangential and swirl velocities,temperature and Nusselt number function (cone surface temperature gradient) are presented.
In these figures,Dax=Daθ=1.0i.e.,the regime is isotropic.Figure 2 shows that an increase in the spin parameter,NR,strongly elevates tangential velocity,due to the induced axial flow,in particular close to the cone surface(y=0),this pattern has been observed also by Ece[9].The principal influence of NRwill be on the tangential momentum since this parameter arises in the tangential momentum Eq.(16),although itis coupled to the swirl momentum.This parameter effectively entails the swirl momentum effect on the tangential momentum.Tangential momentum boundary layer thickness decreased close to the cone surface.Swirl velocity (Fig.3) weakly decreased near the cone surface implying that swirl momentum boundary layer thickness slightly increased in this vicinity.Temperature,H ,(Fig.4) is quite significantly reduced with increasing NRmanifesting with a decrease in thermal boundary layer thickness.In consistency with Fig.4 the heat transfer rate magnitudes (Fig.5) are elevated near the cone surface.The decrease in temperatures in the thermal boundary layer is caused by an enhancement in heat flux to the cone surface which cools the boundary layer.

Fig.5 Temperature gradient(H ′)for various NR(Pr=0.7,Daθ=Dax=1.0)

Fig.6 Tangential velocity (F′)for various Daθ(P r=0.7,NR=5.0,Dax=1.0)
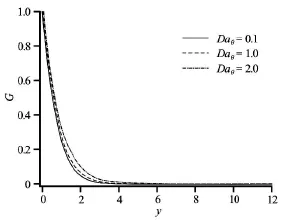
Fig.7 Swirl velocity (G)for various Daθ(P r=0.7,NR= 5.0,Dax=1.0)
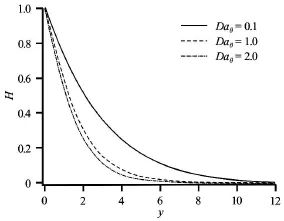
Fig.8 Temperature (H)for various Daθ(P r=0.7,NR= 5.0,Dax=1.0)

Fig.9 Temperature gradient (H ′)for various Daθ(P r=0.7,NR=5.0,Dax=1.0)
Figures 6-9 illustrate the influence of tangential Darcy number,Daθi.e.,θ-direction permeability function on the flow characteristics.IncreasingDaθmarkedly elevates the tangential velocity,F′,close to the wall (Fig.6),further from the cone surface however the effect is reversed and there is a slight decrease in tangential velocities as we progress further into the boundary layer.In close proximity to the wall,the decreased porous media drag caused by a reduction in the presence of porous media fibers in the θ-direction (i.e.,an increase inDaθ) will act to accelerate the flow.Skin friction i.e.,surface shear stress will therefore also be augmented considerably with increasingDaθvalues.Swirl velocity (Fig.7) exhibits a very different response pattern,peakGvalues alwaysarise at the wall and decay smoothly to a minimum in the free stream.However the increase in Daθi.e.,slightly enhances the swirl velocity throughout the boundary layer (the flow is accelerated).Irrespective of the value ofDaθthere never arises any flow reversal in the boundary layer regime.The influence of tangential Darcy number however extends more deeply into the boundary layer transverse to the cone surface for tangential flow compared with swirl flow.With increasingDaθ,temperatures (Fig.8) are substantially reduced in the boundary layer regime.Increasing permeability decreases the concentration of solid particles in the regime i.e.,increases the presence of voids.This serves to suppress thermal conduction heat transfer in the regime and acts to reduce temperatures.There will be a corresponding increase with heat transfer rate magnitudes (Fig.9) to the cone surface however with increasing values ofDaθThe influence Daθ,on the temperature field is less prominent than on the tangential and swirl velocity fields,since Darcy impedance body forces do not feature in the energy conservation Eq.(18).It is therefore expected that a change inDaθ,will affect tangential and swirl velocities to a much greater extent as demonstrated by Figs.6,7.We further note that the swirl velocities are influenced more strongly by thekθthan the tangential velocities,since Daθarises only in the swirl momentum Eq.(17) and will,via coupling,indirectly influence the tangential momentum Eq.(16).
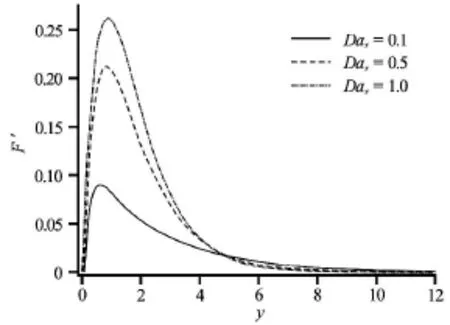
Fig.10 Tangential velocity (F′)for various Dax(P r=0.7,NR=Daθ=1.0)

Fig.11 Swirl velocity (G)for various Dax(P r=0.7,NR= Daθ=1.0)
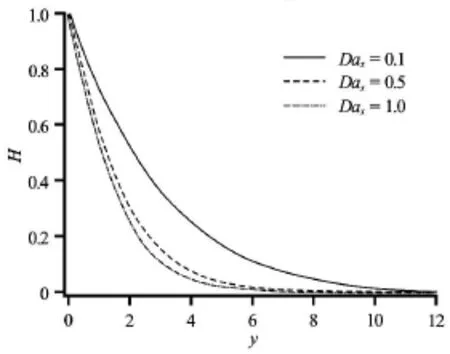
Fig.12 Temperature (H)for various Dax(P r=0.7,NR= Daθ=1.0)

Fig.13 Temperature gradient(H ′)for various Dax(P r= 0.7,NR=Daθ=1.0)
Figures 10-13 illustrate the influence of swirl Darcy number,Daxi.e.,x -direction permeability function on the flow characteristics.A significant acceleration in the tangential velocity is observed in Fig.10,this effect is sustained to a considerable extent into the boundary layer.In the tangential momentum Eq.(16) the Daxparameter arises in the Darcian retarding force term,-F′ Dax.Increasing Daxwill act to decrease the Darcian drag force which will effectively accelerate tangential flow.In Fig.11 we note that a small decrease in the swirl velocity is computed with increasing theDaxparameter.The dominant influence is on the tangential flow (Fig.5).Temperature,His however found to be strongly decreased with increasing Dax.As indicated earlier with progressive increase in permeability,the regime comprises a lower quantity of solid material fibers,this suppresses thermal conduction and acts to cool the boundary layer.This is important in spin coating operations since it achieves excellent thermal control.Surface temperature gradient (H ′)is enhanced in magnitude with increasing swirl Darcy number (Fig.13) in particular close to the cone surface.The flux of heat away from the body of fluid (boundary layer) to the wall therefore decreases thermal boundary layer thickness.

Fig.14 Tangential velocity(F′)for variousPr (Daθ=NR=Dax=1.0)

Fig.15 Swirl velocity(G)for variousPr (Daθ=NR= Dax=1.0)
Finally Figs.14-17,present the influence of Prandtl number(P r)on the velocity functions and temperature field.Larger Pr values (e.g.,Pr =7,corresponds to certain water-based polymeric solutions) and are associated with a thinner thermal boundary layer thickness and more uniform temperature distributions across the boundary layer.Smaller Pr fluids(e.g.,Pr =0.1corresponds to gaseous suspensions)which possess higher thermal conductivities allow heat to diffuse away from the cone surface faster than for higher Pr fluids (low Pr fluids correspond to thicker thermal boundary layers).Pr defines the ratio of momentum diffusivity to thermal diffusivity for a given fluid implying that for lower Pr fluids,heat diffuses faster than momentum and vice versa for higher Pr fluids.For Pr =1the momentum and thermal boundary layers are of the same thickness.For Pr≫1,(e.g.,10) the thermal boundary layer is embedded in the momentum boundary layer since the Prandtl number is much larger than unity and free convection effects are damped thereby contributing less to driving the fluid motion.With increasing Pr ,the tangential velocity (Fig.14) is very strongly decelerated,swirl velocity (Fig.15) is however slightly elevated owing to a re-distribution in momentum in the regime.Temperature,H ,as expected,is markedly suppressed throughout the boundary layer regime(Fig.16),with an increase in Pr .Maximum H corresponds to the lowest Pr value (0.7) since thermal conductivities are much higher for such cases.Heat transfer rates (Fig.17) are elevated in magnitude,in particular close to the cone surface with an increase in Prandtl number.Larger Prandtl number fluids therefore achieve a consistent cooling of the thermal boundary layer.

Fig.16 Temperature (H)for various Pr (Daθ=NR= Dax=1.0)
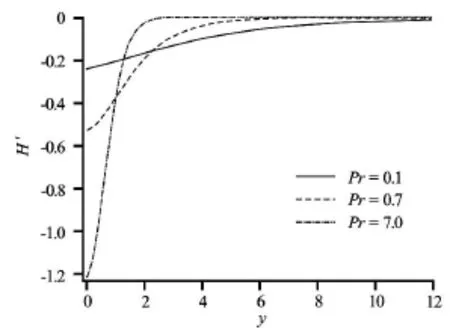
Fig.17 Temperature gradient(H ′)for variousPr (Daθ= NR=Dax=1.0)
Tables 1 and 2 further show that with an increase in spin parameter,the primary skin friction (tangential velocity gradient) i.e.,(F ′)is very strongly enhanced whereas with an increase in Prandtl number it is depressed.The near the surface of rotation is forced radially outwards with a simultaneous upward flow induced tangential to the spinning body surface.The NR=(R esinj)2/Grparameter relates inertial forces to buoyancy forces.As this parameter increases the tangential momentum is boosted and this accelerates the tangential flow leading to a rise in primary skin friction.The increase in Prandtl number has the opposite effect.WhenPris larger,heat diffuses very slowly compared to the velocity (momentum).The thickness of thermal boundary layers is much lower than the velocity boundary layer.The thickening of the momentum boundary layer corresponds to a deceleration in the flow which explains the fall in primary skin friction (tangential velocity gradient) i.e.,(F ′)with larger Prandtl numbers.
5.Conclusion
A mathematical model has been developed for the free convection flow from a rotating cone embedded in an anisotropic Darcian highly permeable medium.The governing equations have been rendered into self-similar form with appropriate scaling transformations,subject to physically realistic boundary conditions.MAPLE quadrature numerical solutions are developed for the resulting ordinary differential boundary value problem.Validation is achieved with previous solutions[9]and a Galerkin finite element code,showing excellent agreement.Tangential and swirl velocities have been found to be generally elevated with increasing permeability functions (i.e.,Darcy parameters) owing to a corresponding reduction in the Darcian body forces.Increasing spin velocity of the cone has been shown to boost the tangential velocities but only slightly reduce the swirl velocity.Heat transfer rates are also found to be strongly affected by anisotropic Darcy numbers and the spin parameter.The present model is Newtonian.Future studies will examine non-Newtonian nanofluids[23]and will be communicated imminently.
[1]KREITH F.Convection heat transfer in rotating systems[J].Advances in Heat Transfer,1968,5:129-251.
[2]MAKARYTCHEV S.V.,LANGRISH T.A.G.and PRINCE R.G.H.Thickness and velocity of wavy liquid films on rotating conical surfaces[J].Chemical Engineering Science,2001,56(1):77-87.
[3]ADACHI T.Oxygen transfer and power consumption in an aeration system using mist and circulation flow generated by a rotating cone[J].Chemical Engineering Science,2015,126:625-632.
[4]CHAMKHA A.J.,RASHAD A.M.Unsteady heat and mass transfer by MHD mixed convection flow from a rotating vertical cone with chemical reaction and Soret and Dufour effects[J].The Canadian Journal of Chemical Engineering,2014,92(4):758-767.
[5]OSALUSI E.,SIDE J.and HARRIS R.et al.The effect of combined viscous dissipation and Joule heating on unsteady mixed convection MHD flow on a rotating cone in a rotating fluid with variable properties in the presence of Hall and ion-slip currents[J].International Communications in Heat and Mass Transfer,2008,35(4):413-429.
[6]NARAYANA M.,AWAD F.G.and SIBANDA P.Free magnetohydrodynamic flow and convection from a vertical spinning cone with cross-diffusion effects[J].Applied Mathematical Modelling,2013,37(5):2662-2678.
[7]ANILKUMAR D.,ROY S.Unsteady mixed convection flow on a rotating cone in a rotating fluid[J].Applied Mathematics and Computation,2004,155(2):545-561.
[8]RAJU S.H.,MALLIKARJUNA B.and VARMA S.V.K.Thermophoretic effect on double diffusive convective flow of a chemically reacting fluid over a rotating cone in porous Medium[J].International Journal of Scientific and Engineering Research,2015,6(1):198-204.
[9]ECE M.C.Free convection flow about a vertical spinning cone under a magnetic field[J].Applied Mathematics and Computation,2006,179(1):231-242.
[10]VAFAI K.Handbook of porous media[M].New York,USA:Marcel Dekker,2005.
[11]BÉG O.A.,ZUECO J.and TAKHAR H.S.et al.Transient non-linear optically-thick radiative-convective double-diffusive boundary layers in a Darcian porous medium adjacent to an impulsively started surface:Network simulation solutions[J].Communications in Nonlinear Science and Numerical Simulation,2009,14(11):3856-3866.
[12]MCKIBBIN R.Convection and heat transfer in layered and anisotropic porous media (QUINTARD M.,TODOROVIC M.Editors.Heat and mass transfer in porous media)[M].Amsterdam,The Netherlands:Elsevier,1992,327-336.
[13]WHITE R.E.,SUBRAMANIAN V.R.Computational methods in chemical engineering with maple[M].Berlin,Heidelberg,Germany:Spring-Verlag,2010.
[14]BHARGAVA R.,SHARMA S.and BÉG O.A.et al.Finite element study of nonlinear two-dimensional deoxygenated biomagnetic micropolar flow[J].Communications in Nonlinear Science and Numerical Simulation,2010,15(5):1210-1223.
[15]BÉG O.A.,LIK S.and ZUECO J.et al.Numerical study of magnetohydrodynamic viscous plasma flow in rotating porous media with Hall currents and inclined magnetic field influence[J].Communications in Nonlinear Science and Numerical Simulation,2010,15(2):345-359.
[16]BÉG O.A.,UDDIN M.J.and KHAN W.A.Bioconvective non-Newtonian nanofluid transport in porous media containing micro-organisms in a moving free stream[J].Journal of Mechanics in Medicine and Biology,2015,15(5):1550071.
[17]MAKINDE O.D.,BÉG O.A.and TAKHAR H.S.Magnetohydrodynamic viscous flow in a rotating porous medium cylindrical annulus with an applied radial magnetic field[J].International Journal of Applied Mathematics and Mechanics,2009,5(6):68-81.
[18]SEMMAH A.,BÉG O.A.and MAHMOUD S.R.et al.Thermal buckling properties of zigzag single-walled carbon nanotubes using a refined nonlocal model[J].Advances in materials Research,2014,3(2):77-89.
[19]UDDIN M.J.,YUSOFF N.H.M.and BÉG O.A.et al.Lie group analysis and numerical solutions for non-Newtonian nanofluid flow in a porous medium with internal heat generation[J].Physica Scripta,2013,87(2):25401-25414.
[20]CHUNG T.J.The finite element method in fluid flow[M].New York,USA:Wiley,1978.
[21]BÉG O.A.,RAWAT S.and ZUECO J.et al.Finite element and network electrical simulation of rotating magnetofluid flow in nonlinear porous media with inclined magnetic field and Hall currents[J].Theoretical and Applied Mechanics,2014,41(1):1-35.
[22]BÉG O.A.Numerical methods for multi-physical magnetohydrodynamics,Chapter 1 (New developments in hydrodynamics research)[M].New York,USA:Nova Science,2012,1-112.
[23]PRASAD V.R.,GAFFAR S.A.and BÉG O.A.Heat and mass transfer of a nanofluid from a horizontal cylinder to a micropolar fluid[J].Journal of The rmophysics and Heat Transfer,2014,29(1):1-13.
10.1016/S1001-6058(16)60620-0
(Received May 11,2015,Revised June 25,2015)
* Biography:O.Anwar BÉG (1969-),Male,Ph.D.,Professor
M.J.UDDIN,E-mail:jashim_74@yahoo.com
2016,28(2):184-194
- 水动力学研究与进展 B辑的其它文章
- Manoeuvring prediction based on CFD generated derivatives*
- Effects of water flow on the uptake of phosphorus by sediments:An experimental investigation*
- Improved formulas for thermal behavior of oscillating nanobubbles*
- Lattice Boltzmann method for Casimir invariant of two-dimensional turbulence*
- The experiment and analysis of transitional flow in pipe*
- Numerical simulation of 3-D free surface flows by overlapping MPS*

