Improved formulas for thermal behavior of oscillating nanobubbles*

Yu-ning ZHANG （张宇宁），Shengcai LI

1.State Key Laboratory of Water Resources and Hydropower Engineering Science，Wuhan University，Wuhan 430072，China

2.Key Laboratory of Condition Monitoring and Control for Power Plant Equipment，Ministry of Education，North China Electric Power University （Beijing），Beijing 102206，China

3.School of Engineering，University of Warwick，Coventry CV4 7AL，UK，E-mail:y.zhang@ncepu.edu.cn

Improved formulas for thermal behavior of oscillating nanobubbles*

Yu-ning ZHANG （张宇宁）1，2，3，Shengcai LI3

1.State Key Laboratory of Water Resources and Hydropower Engineering Science，Wuhan University，Wuhan 430072，China

2.Key Laboratory of Condition Monitoring and Control for Power Plant Equipment，Ministry of Education，North China Electric Power University （Beijing），Beijing 102206，China

3.School of Engineering，University of Warwick，Coventry CV4 7AL，UK，E-mail:y.zhang@ncepu.edu.cn

The study of nanobubbles （with sizes of the order of tens to hundreds of nanometers） is currently a hot spot of cavitation and bubble dynamics.In the literature，classical formulas are widely employed for the predictions of the thermal behavior of oscillating macro-bubbles.However，for modelling nanobubbles，the classical formulas may not be adequate due to the effects of the surface tension.In the present paper，a formula with the effects of surface tension fully considered is proposed for the predictions of thermal behavior.The predictions based on the classical formula are also presented for comparisons to show the advantages of the present formula.

nanobubbles，cavitation，thermal behavior，surface tension

Nanobubbles are bubbles with sub-micro sizes and gas inside in the aqueous solution.Recently，the presence of stable surface nanobubbles has attracted intensive studies［1，2］.Those surface nanobubbles have many unique characteristics，leading to plenty of applications in the industry［1］.For example，the surface nanobubbles could have a long lifetime up to several days［1］.The production of surface nanobubbles can be easily achieved through the so-called standard solvent exchange procedure （i.e.，exchange of short-chain alcohol with water on solid substrate）.The gaseous nature of surface nanobubbles has also been confirmed by experimental studies［1］.Lohse and Zhang［1］gave a full review of surface nanobubbles.

Owing to the small size of nanobubbles，many classical formulas may not be valid.For example，the classical diffusion theory predicts that the nanobubbles should be totally dissolved into the solution throughthe mass diffusion within tens of microseconds.However，the air nanobubbles could persist for more than four days，suggesting a new mechanism beyond the classical theory［1］.Similarly，the thermal behavior of nanobubbles has its features.The thermal damping mechanism is one of the important aspects for accurate modeling of bubbles.The thermal damping mechanism of macro-bubbles has been investigated by many researchers over several decades.Assuming a uniform pressure inside the gas bubbles，Devin［3］derived an analytical formula for the predictions of the thermal damping mechanism，which is currently highly cited in the literature and has been widely quoted by many textbooks and research papers.Formulas related with the thermal damping mechanism are widely employed for revealing underlying physics in the bubble phenomenon，e.g.，the rectified mass diffusion，the wave propagation in bubbly liquids，the acoustical scattering，the bubble instability，the bubble-bubble interaction，and the sonoluminescence.Zhang［4］gave a brief review of the models for thermal effects.

In the present paper，the thermal behavior of spherical nanobubbles in the liquids are theoretically investigated.After a close re-examination of the classical formula，it is found that the effects of the surface tension are not fully considered in the aforementioned formula，leading to a less accurate prediction of the nanobubble behaviors.

In this section，the classical work by Devin［3］onthe spherical bulk bubbles will be introduced with details.The following assumptions are used［3］:

（1） The liquid temperature adjacent the bubble interface does not change so the liquid behaves as a heat reservoir［3］.Therefore，the equation of the energy conservation in the liquid was not solved in Ref.［3］.

（2） The density and the specific heats of the gas are regarded as constants［3］.

（3） The pressure in the gas bubbles is uniformly distributed.Therefore，the pressure in the gas is only a function of the time but not the radial coordinate［3］.

（4） The boundary conditions on the bubble interface and at the bubble center are given as follows［3］:at the center of the bubble，the changes of the temperature must be finite and the gradient of the change of the temperature must be zero，on the bubble-liquid interface，the changes of the temperature must be zero and the gradient of the change of the temperature must be finite.If we define θ1as the change of the temperature inside the gas bubbles from the equilibrium absolute temperature，the boundary conditions at the center of the bubble areθ1→∞and dθ1/dt=0 while the boundary conditions on the bubble-liquid interface are θ1=0and dθ1/dt→∞.

（5） The oscillations of the pressure，the bubble volume and the temperature are assumed to be small［3］.

In this section，the key points of the derivation process of Devin［3］is summarized.Here，most notations of Devin［3］are retained.

By differentiating the first law of thermodynamics，one obtains，

with

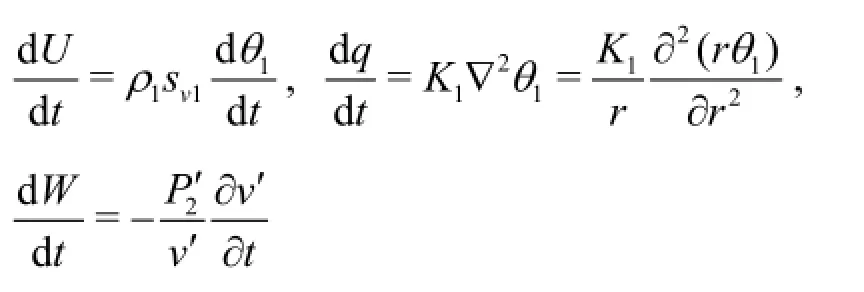
Here，U is the internal energy of the gas bubble，qis the amount of heat transferred，Wis the work done on the gas bubbles，t is the time，ρ1is the gas density，sv1is the specific heat of the gas at a constant volume，θ1is the change of the temperature inside the gas bubbles from the equilibrium absolute temperature，K1is the thermal conductivity of the gas，r is the radial coordinate，P2′is the pressure on a infinitesimal spherical shell with volumev′.Using the ideal gas law，v′in Eq.（1） can be eliminated，resulting in a differential equation of θ1.Then the solution of θ1can be obtained through solving this differential equation with related boundary conditions.

Using the ideal gas law again，the dynamic volume of the oscillating gas bubble can be obtained.By employing the equation of the bubble motion，the stiffness and the energy loss caused by the thermal damping mechanism can both be obtained.

For convenience，the dissipation of the energy through the thermal damping mechanism is represented by a term related with the “effective thermal viscosity （µth）” as done in Ref.［3］.The non-dimensional thermal damping constant（δth）is defined by Devin［3］as

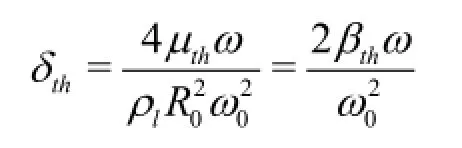
Here，ωis the angular frequency of the driving sound field，µthis the effective thermal viscosity，ρlis the liquid density，R0is the equilibrium bubble radius，ω0is the natural frequency of the oscillating gas bubbles，and βthis the thermal damping constant.Devin［3］gave the expression of δas follows:

th

where

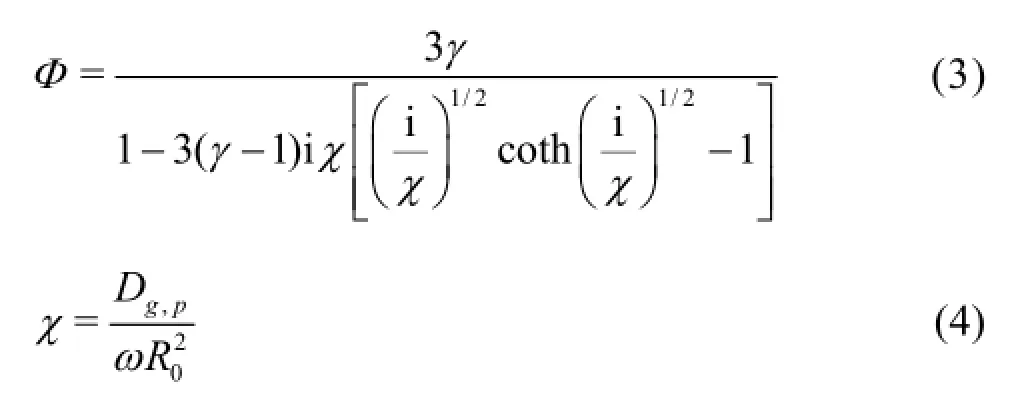
Here，Im and Redenote the imaginary and real parts of the function，respectively，Dg，pis the thermal diffusivity of the gas at a constant pressure，γ is the ratio of the specific heats of the gas.Eqs.（2）-（4） is the widely cited formulas for the predictions of the thermal damping behavior of the oscillating bubbles.In Eqs.（3） and （4），the notations of Prosperetti are employed.

After the derivation of Devin's formulas as shown in the last section，it is found that the effects of the surface tension has not been fully considered.Hence，in this section，a correction is made following the framework of Devin［3］with most of his notations retained.

In Eq.（4） of Devin［3］，the instantaneous pressure on the bubble interface （P2′）can be represented by the sum of two terms as follows

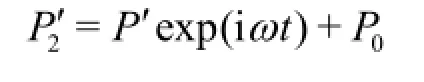
Here，P′is the complex amplitude of the pressure change from the equilibrium state，P0is the ambient pressure.With the surface tension included，the above equation should be written as

where

Here，Pin，eqis the equilibrium pressure in the gas，σ is the surface tension coefficient.Because Devin［3］assumed that the pressure inside the gas bubble is uniformly distributed，P2′andP′are only functions of the time（t）but not the radial coordinate （r）.Hence，P′can also be considered as the （uniform） instantaneous pressure inside the gas bubbles.

Based on the first law of thermodynamics，the deviation of the absolute temperature （θ1（r，t））from the equilibrium absolute temperature （T0）was determined by Eqs.（38） and （40） of Devin［3］.The expression of θ1（r，t）is not influenced by the surface tension.For a spherical shell with radius rand thicknessdr，the equilibrium volume of the shell （v0）can be written as Eq.（41） of Ref.［3］

Based on the law of the ideal gas，with the correction of the effects of the surface tension，one can obtain

with

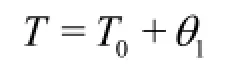
Here，v is the deviation of the volume of the shell from the equilibrium volume v0，Tis the instantaneous absolute temperature inside the gas bubbles.Following Eqs.（43）-（47） of Devin［3］and differentiating both sides of Eq.（7） and integratingdνfrom r =0to r=R0，one can obtain the deviation of the total bubble volume（V′）from the equilibrium total bubble volume （V0）as follows

Here，Φis given by Eq.（3）.P0in Eq.（47） of Devin［3］is replaced byPin，eqto include the effect of the surface tension.Assuming that the instantaneous bubble radius（R）is

Here，x is the non-dimensional amplitude of the oscillations of the instantaneous bubble radius.Then，based on Eq.（49） of Devin［3］，one can obtain

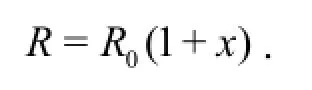
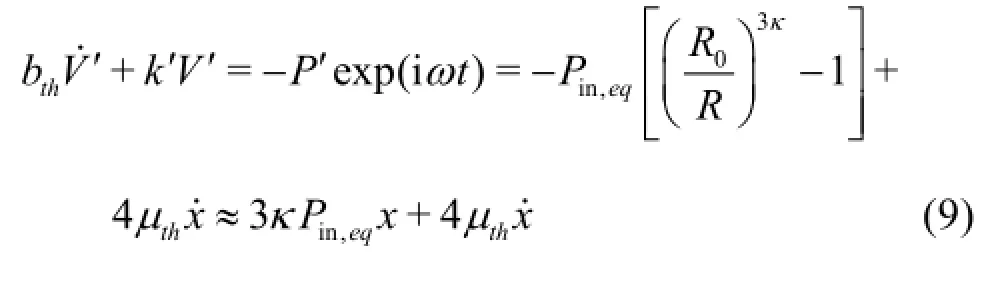
Here，the dot over a variable denotes its time derivative，k is the polytropic exponent，bthis the dissipation coefficient.The meaning of k′will be explained later.Noticing that，one can obtain

In Eq.（9），the restoring stiffness kused by Eq.（49） of Devin［3］is replaced byk′because the two expressions are not identical if the surface tension is considered.With the surface tension included，the expression of the stiffnesskis

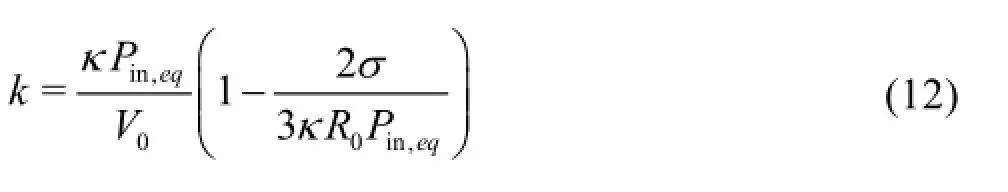
Therefore，k in Eq.（12） reduces tok′in Eq.（11）when the surface tension in Eq.（12） is neglected.Alternatively，δthdefined by Devin［3］can be expressed as

Substituting Eq.（8） into Eq.（9），bthand k′can be expressed as functions ofΦ.Furthermore，using Eqs.（12） and （13），one can obtain expressions for k and δthas follows:

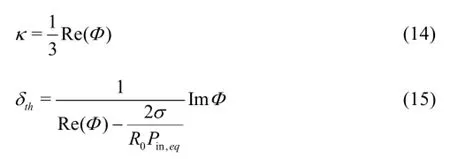
Comparing with Eq.（2） derived by Devin［3］，one can see a term involving the surface tension in the denominator of Eq.（15）.The expression of the polytropic exponent in Ref.［3］is not influenced by the correction of the surface tension.

In this section，some demonstrating examples will be given to show the effects of the surface tension（i.e.，the difference between Eq.（2） by Ref.［3］and Eq.（15） by us） in predicting the thermal damping mechanism during the radial oscillations of the gas bubbles in liquids under the acoustic excitation.For simplicity，the air bubbles oscillating in water are considered with the following constants:Dg，p=2.08× 10-5m2/s，σ=72.8dyn/m ，P0=1.01× 105Pa，γ=1.40.In the following discussions，the normalized error of the predictions of the non-dimensional thermal damping constant（δth）between Eq.（2） and Eq.（15） will be shown.

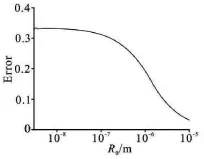
Fig.1 Normalized error of the predictions of non-dimensional thermal damping constant （δth）by the formulas with and without corrections of surface tension （referring to Eq.（15） and Eq.（2） respectively） for air bubbles oscillating in water

Figure 1 compares the predictions of the normalized error of the non-dimensional thermal damping constant （δth）with or without the effects of the surface tension considered （referring to Eq.（15） and Eq.（2），respectively）.The predictions ofδthwithout the surface tension considered （Eq.（2）） are lower than those with the surface tension considered （Eq.（15）） for small bubbles，leading to the normalized error more than 30% for the nanobubbles.Hence，Eq.（15） should be employed for bubbles with radii within the range of micrometers，which drops into the regions of currently widely used microbubbles in the biomedical engineering （e.g.，in the tumor treatment based on the acoustic cavitation） and nanobubbles.Based on the analysis of a large amount of nanobubbles observed in the experiment，it is found that the radii of the nanobubbles are less than 2 µm［1］.For those nanobubbles，the surface tension plays a major role in their physical processes（e.g.，the thermal damping mechanism during their oscillations） and should be fully considered.For macro bubbles （e.g.，bubbles with sizes more than 10 micrometers），the normalized error shown in Fig.1 is within 10%，hence the correction proposed here is not important.

At the end of this section，several limitations of the present paper will be discussed.In the present paper，many assumptions are adopted in order to obtain a simple analytical solution.In fact，the violent bubble motion could also be involved when the nanobubble is near the surface.Those details may be found in Ref.［1］for recent progress and Refs.［5-7］for the dynamics of macroscopic bubbles as a comparison.In the current cavitation models，only bubbles with sizes above several micrometers are considered as the cavitation bubble nuclei.The existence of nanobubbles also requires a further refinement of the current cavitation model （e.g.，the cavitation model based on the mass transfer equation） to incorporate the effects of nano-scale bubbles for industrial scale applications［8］.

In the present paper，for modelling nanobubbles，a correction based on a well-known formula for the predictions of the thermal behavior is proposed for fully considering the effects of surface tension.The formula of the thermal damping constant will be influenced by this correction while the formula of the polytropic exponent will not.This corrections will be prominent for bubble sizes in the range of several micrometers.

［1］LOHSE D.，ZHANG X.Surface nanobubbles and nanodroplets［J］.Reviews of Modern Physics，2015，87（3）:981-1035.

［2］YASUI K.，TUZIUTI T.and KANEMATSU W.et al.Advanced dynamic-equilibrium model for a nanobubble and a micropancake on a hydrophobic or hydrophilic surface［J］.Physical Review E，2015，91（3）:033008.

［3］DEVIN Jr C.Survey of thermal，radiation，and viscous damping of pulsating air bubbles in water［J］.The Journal of the Acoustical Society of America，1959，31（12）:1654-1667.

［4］ZHANG Y.Heat transfer across interfaces of oscillating gas bubbles in liquids under acoustic excitation［J］.International Communications in Heat and Mass Transfer，2013，43（2）:1-7.

［5］ZHANG A.M.，CUI P.and CUI J.，et al.Experimental study on bubble dynamics subject to buoyancy［J］.Journal of Fluid Mechanics，2015，776:137-160.

［6］ZHANG A.M.，LI S.and CUI J.Study on splitting of a toroidal bubble near a rigid boundary［J］.Physics of Fluids，2015，27:062102.

［7］ZHANG A.M.，LIU Y.L.Improved three-dimensional bubble dynamics model based on boundary element method［J］.Journal of Computational Physics，2015，294:208-223.

［8］ZHANG Y.，QIAN Z.and JI B.et al.A review of microscopic interactions between cavitation bubbles and particles in silt-laden flow［J］.Renewable and Sustainable Energy Reviews，2016，56:303-318.

10.1016/S1001-6058（16）60635-2

（Received October 3，2015，Revised January 14，2016）

* Project supported by the National Natural Science Foundation of China （Grant No.51506051），the Open Research Fund Program of State Key Laboratory of Water Resources and Hydropower Engineering Science，Wuhan University （Grant No.2014SDG01）.

Biography:Yu-ning ZHANG （1983-），Male，Ph.D.，Associate Professor

2016，28（2）:325-328