关于分裂凸可行性问题的粘性迭代算法

杨远志，杨海元，李春，何振华



关于分裂凸可行性问题的粘性迭代算法

杨远志，杨海元，李春，何振华

（红河学院 数学学院，云南 蒙自 661199）

研究了分裂凸可行性问题，给出了该问题的一个新的近似解算法，并证明该算法具有强收敛性，所获得的结果改进了前人的工作．

分裂凸可行性问题；近似解；强收敛；粘性迭代方法

1引言及预备知识

找出一点，使得（1）

该问题在许多实际问题都有应用，如图像恢复（重建）和信号处理等．当问题（1）解存在时，那么其解满足一个不动点方程，其中：表示度量投影算子；表示的伴随算子；是一常数．

为求解问题（1），Byrne在文献[2]中建立了近似解算法：，其中：和分别表示投影算子；表示的共轭算子；是一个常数，，是的谱半径．Byrne证明了该序列收敛到问题（1）的一个解．

找出，，使得（2）

文献[3]的算法仅仅是弱收敛算法，在实际应用中，强收敛算法更为方便，而且，算法中仅仅简单地使用投影方法计算问题的近似解，这有可能使得算法的收敛速度比较慢．针对这些问题，本文建立了粘性迭代算法，证明在适当的条件下，新算法强收敛到问题（2）的一个解．

定义1[4]107设是域上的线性空间，若对于任意，有一个中的数与之对应（用表示该数），使得对于任意，，有

定义2[4]59（1）设是内积空间，，如果对于任意，，，有，则称是中的线性算子．若还满足（），是与无关的常数，则称是有界线性算子．

引理1[5]3310设为实Hilbert空间，则对于任意，有．

引理2[6]设是非负实数列，满足，．若，，且，则．

引理3（半闭原理）[7]设为实Hilbert空间，，：是非扩张映射，若弱收敛到，并且，则．

引理4[5]3318设为实Hilbert空间，则对于任意，有．

2主要结果及证明

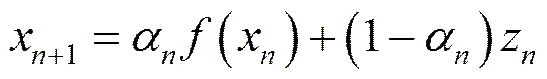
又

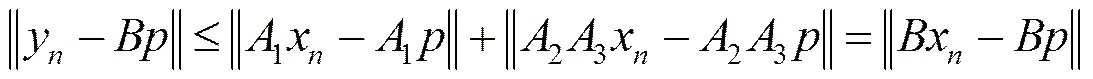
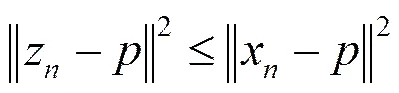
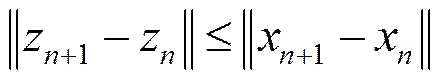
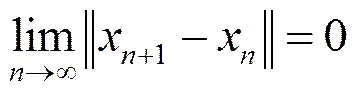
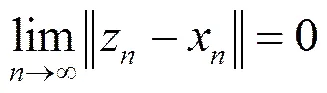
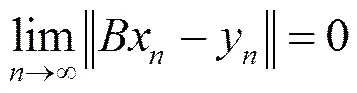
于是

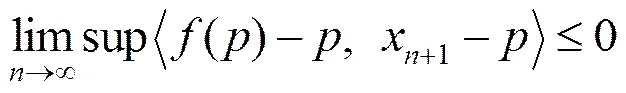
虽然推论2是定理的特例，但是由于定理中包含的压缩映射的值是随着迭代过程一起变化的，因此其收敛速度会跟着受到影响．

本文讨论了分裂可行性问题，给出了该问题近似解的一个新算法，并证明了该算法具有强收敛性，推广了已有文献的结果．与文献[3]中的算法比较，虽然本文迭代算法也包含了投影算子，但是引入了压缩映射．因此，建立的新算法可以通过压缩映射调节其收敛速度，这样可以实现更快速度的收敛．

[1] Censor Y，Elfving T．A multiprojection algorithm using Bregman projections in a product space[J]．Numerical Algorithms，1994 （8）：221-239

[2] Byrne C．Iterative oblique projection onto convex sets and the split feasibility problem[J]．Inverse Problems，2002（18）：441-453

[3] Mouda A．A relaxed alternating CQ-algorithm for convex feasibility problems[J]．Nonlinear Anal，2013（79）：117-121

[4] 刘炳初．泛函分析[M]．2版．北京：科学出版社，2007

[5] Chang S S，Lee H W J，Chan C K．A new method for solving equilibrium problem fixed point problem and variational inequality problem with application to optimization[J]．Nonlinear Anal，2009（70）：3307-3319

[6] Xu H K．Iterative algorithms for nonlinear operators[J]．J London Math Soc，2002（2）：240-256

[7] Takahashi W．Nonlinear Functional Analysis，Fixed Point Theory and Its Applications[M]．Yokohama：Yokohama Publishers， 2000

[8] Marino G，Xu H K．Weak and strong convergence theorems for strict pseudo-contractions in Hilbert spaces[J]．J Math Anal Appl， 2007（329）：336-346

A viscosity iteration algorithm for the split convex feasibility problem

YANG Yuan-zhi，YANG Hai-yuan，LI Chun，HE Zhen-hua

（School of Mathematics，Honghe University，Mengzi 661199，China）

Studied the split convex feasibility problem，a new approximate solution algorithm for this problem was given，and show that the algorithm converges strongly to a solution of this problem．The results obtained in this paper improved previous works．

split convex feasibility problem；approximate solution；strong convergence；viscosity iteration method

1007-9831（2016）04-0022-06

O177.19

A

10.3969/j.issn.1007-9831.2016.04.006

2015-12-10

红河学院大学生创新创业训练项目（DCXL1315）；红河学院后备人才项目（2014HB0206）

杨远志（1993-），男，云南保山人，在读本科生．E-mail：1740993919@qq.com

何振华（1979-），男，广西藤县人，教授，在读博士研究生，从事非线性分析研究．E-mail：zhenhuehe@126.com