基于预测控制与H∞控制的有源电力滤波器设计

马　兴　刘会金　崔　雪　郭晓云　汪文达

(武汉大学电气工程学院　武汉　430072)



基于预测控制与H∞控制的有源电力滤波器设计

马兴刘会金崔雪郭晓云汪文达

(武汉大学电气工程学院武汉430072)

为了能更准确地分析有源电力滤波器(APF)系统，建立了考虑时滞、参数摄动以及死区干扰等的APF时滞不确定性模型，并设计了系统的时滞H∞鲁棒控制器。然而在该控制策略下，要保证系统鲁棒稳定性，就会严重降低干扰抑制能力，使APF系统的补偿效果受到影响。针对这一问题，采用嵌入预测控制的方法将APF的时滞不确定性模型转换为不含时滞的不确定性模型，采用H∞控制方法对标称系统设计控制器，以保证系统的整体稳定性，利用参数摄动造成的状态变量扰动是周期性的特性，采用PI控制与重复控制构成的复合控制策略消除参数摄动带来的影响。最后采用Matlab仿真及物理实验对其可靠性进行了验证。

有源电力滤波器时滞系统预测控制H∞控制重复控制

0　引言

由于传感器、前置滤波器及数字化控制造成的延时，有源电力滤波器(Active Power Filter，APF)系统是一个典型的时滞系统。目前对于有源电力滤波器已有大量研究，基于APF状态空间模型，文献[1，2]采用了无源性控制策略设计方法；文献[3，4]采用了L2增益控制策略设计方法，考虑了参数摄动的影响；文献[5-7]采用了Lyapunov函数控制策略设计方法，分析了参数摄动及时滞的影响；文献[8，9]采用了H∞鲁棒控制设计方法，同时考虑了参数摄动和未建模部分。这些方法从本质上都可以归为Lyapunov稳定性方法，然而这些方法采用的是APF无时滞的理想模型，均未考虑时滞对系统稳定性及补偿效果可能带来的影响。文献[10]提出在检测部分采用信号预测的方法消除时滞影响，明显提高了补偿效果，然而在控制器中包含APF输出电流项仍存在时滞，使得控制系统仍是时滞系统，该项的存在造成对较高频次的谐波补偿效果较差，并且在负载较轻的情况下，整体补偿效果仍然较差，在配电网中使用的APF由于需要面对各种负载状态，应要求在轻载下仍能有较好的补偿效果。

为了使APF系统在同时考虑时滞、参数摄动及包含死区的其他未建模干扰下，能够严格稳定且进一步提高补偿性能，本文提出了APF的时滞不确定性状态空间模型，设计了APF系统的时滞H∞鲁棒控制器。在控制器的设计中，可以看到满足系统鲁棒渐进稳定性，大大减小了控制增益的取值，而控制增益过小严重降低了干扰抑制能力，最终使得补偿效果变差。由于控制器中仍存在时滞项，即使检测部分采用信号预测，控制系统仍具有时滞性，依然满足该分析。在仿真试验中，控制增益越小补偿效果越好，开环下的补偿效果最好，说明补偿能力有极限。

本文提出了采用嵌入预测控制的方法从模型结构上改变APF的时滞模型。通过引入反馈校正预测控制对APF未来输出电流进行预测，利用该预测值作为未来电流的估计值，使模型中不含时滞项，整个模型变为无时滞模型。对于嵌入预测控制后的标称系统采用H∞控制方法设计控制器，以保证其稳定性。对于参数不确定性带来的影响，单独进行考虑，利用APF的参数摄动往往是慢时变的，在较短时间内可看作是常数，因而从APF系统模型中可看出其造成的干扰是一个周期性的干扰。引入比例积分(Proportional-Integral，PI)控制与重复控制构成复合控制对这一周期性干扰进行跟踪，并在占空比的计算中将其反向减去以消除干扰。最后采用Matlab搭建了仿真平台，并通过物理实验验证了该方法的有效性。

1　APF时滞不确定性系统模型分析

1.1APF时滞不确定性系统模型

对于三相并联型APF，当采用PWM内层控制时，总时滞包含数字信号处理器(Digital Signal Processing，DSP)的计算延时、PWM的等效时延及传感器和前置滤波器的时延。本文设置APF的采样频率为10 kHz，PWM的载波频率为10 kHz，传感器时延[11]约为3.5×10-5s，传感器和前置滤波器带来的时延为3×10-5～4×10-5s，总时滞约为2倍的采样周期[12-14]。

三相并联型有源电力滤波器的基本原理如图1所示。图中，udc为APF直流侧电容电压，usa、usb、usc为公共连接点(Point of Common Coupling，PCC)三相电压，ila、ilb、ilc为负载侧三相电流，ifa、ifb、ifc为APF输出三相电流，R和L分别为APF交流输出侧的等效电阻和电感，Lx为变压器等效电感，Ls为电网侧等效电感。

图1　三相并联型有源电力滤波器原理图Fig.1　The schematic of three-phase shunt active power filter

如图1所示，APF的dq轴平均化模型为

(1)

式中，pd、pq分别为dq轴下的双极性占空比函数；ifd、ifq分别为三相负载电流转换到dq轴的值，A；usd、usq分别为PCC点三相电压转换到dq轴的值，V；ω为工频角频率，rad/s；wd、wq、wc分别为包含死区效应的未建模部分造成的干扰。由于该模型是一欠驱动系统，对于式(1)中电容电压状态变量方程需间接控制实现，常采用PI控制对APF直流侧电压进行稳压控制，其控制律为

(2)

仅对式(1)中前两行输出电流状态变量方程进行误差系统变换，可得到APF系统的时滞不确定性误差系统模型为

(3)

(4)

(5)

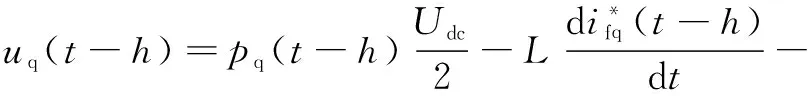
(6)

1.2APF系统基于时滞鲁棒系统控制器设计

将式(3)转换为标准形式

(7)

对于h考虑一定的裕度可以表述为

(8)

式中，τ为时延，τ=2×10-4s；μ为时延变化率，μ=0.2。

对于R/L和工频的摄动，认为R/L的摄动范围为10%，按照国标认为工频的摄动为±0.5 Hz即1%，并将该摄动表示为标准形式

ΔA=DF(t)E, FT(t)F(t)≤I

(9)

式中，D和E为适当维数的常数矩阵；F(t)为时变矩阵。在此基础上，若采用常用的静态控制器U(t)=KX(t)， 则在该控制器下能保证系统稳定且具有γ干扰抑制度的控制器增益矩阵K可以由以下定理得到。

(10)

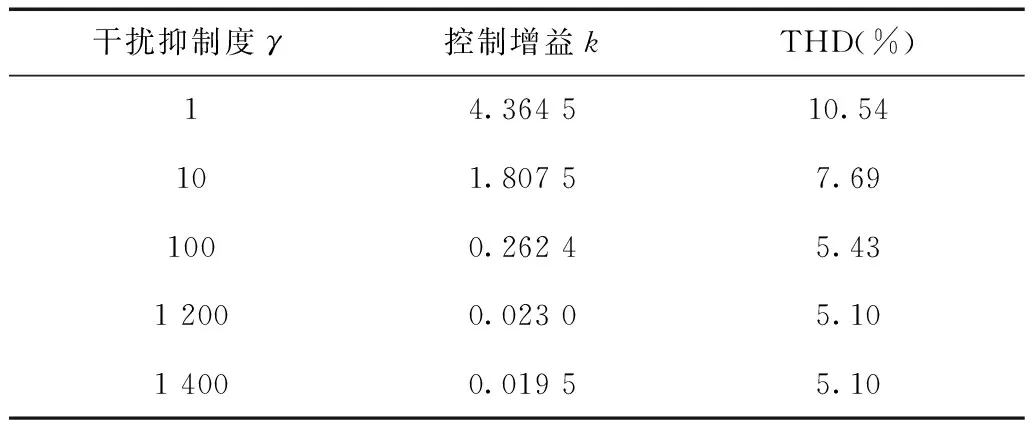
不同的干扰抑制度γ求解系统的控制器，得到的结果如表1所示。

表1　稳定性与干扰抑制关系Tab.1　The relationship between stability and interference suppression

表1中，最后一行的干扰抑制度是采用二分法得出的系统临界稳定的情况，可以看出当干扰抑制度小于临界值时(即对干扰的抑制能力增强)，系统进入不稳定状态；当干扰抑制度大于临界值时(即对干扰的抑制能力下降)，系统的稳定裕度增加。然而从整体上看，系统在考虑时滞及参数摄动的情况下，对干扰的能量起到了放大的作用，即放大了干扰对状态变量的影响，从而使状态变量在原本的渐进状态下发生一定的波动，最终造成补偿效果变差，后面的仿真也说明了该分析的有效性。

闭环系统仍是时滞系统，与之前的分析结果相同。

2　基于预测控制与H∞控制的改进控制器设计

分析式(7)可以看出由于时滞的影响，从等效输入中引入了时滞项，如果能够通过预测控制使得U(t-h)=KX(t)， 则可以将闭环系统转换为不含时滞的系统。本文提出了检测部分采用两步预测、并对状态变量中的φd(t)和φq(t)采用反馈校正预测控制进行估计的方法，实现闭环系统的去时滞。

由前面的分析可知，检测部分采用两步预测能取得较好的效果。对检测部分的两步预测方法较多，本文利用其周期性用上一周期中数据进行估计，对于状态变量中φd(t)和φq(t)的实时值，由于系统延时不能直接通过传感器得到，因此需要采用预测控制进行估计，其反馈预测控制预测律为[15，16]

(11)

式中，λd、λq为预测控制增益，可设定。进一步，选取控制器为

将由式(12)表示的控制器方程带入式(7)中可得

(13)

可见，闭环系统中不存在时滞项，故忽略了变量t，如果存在式(12)所示的控制器能够使式(13)表示的闭环系统渐进稳定且满足干扰抑制条件‖TZW(s)‖≤γ， 则称系统具有状态反馈H∞控制律。

为了便于采用计算机进行处理，将H∞控制律求解转换为线性矩阵不等式(LMI)形式[17]。对于由式(13)所示的APF系统，存在一个状态反馈H∞控制器，且具有γ次干扰抑制增益，当且仅当存在一个对称正定矩阵X和矩阵G，使得矩阵不等式

成立。如果矩阵不等式存在一个可行解X*、G*，则U=G*(X*)-1X是系统的一个γ次优H∞控制器。对于该LMI，干扰抑制度具有很大范围的取值，然而过大的干扰抑制度会造成PWM内层控制饱和(即占空比计算值大于1)，综合考虑干扰抑制度、稳定裕度和内层控制的约束，选择γ=0.3， 对应的控制增益k=17.307 3。

3　对于参数摄动和未建模部分的干扰抑制

可以看到第2节的讨论中并未考虑参数摄动的影响，这是因为APF系统的参数摄动具有特殊性，R和L是慢时变的，因此在一段时间内可以看作是常数，由文献[8]可知摄动造成的干扰基本上是周期性的，因此考虑采用PI控制与重复控制构成的复合控制[18，19]方法实现对周期性干扰的补偿。

如图2所示，采用复合控制[18，19]的方法跟踪状态变量的周期性变化，重复控制保证了对周期性变化的跟踪，PI控制提高了跟踪的速度准确度。由文献[3]可知，死区效应也可以等效为一个工频周期性干扰和一个非周期性干扰。在考虑参数摄动及死区干扰时，式(11)中预测控制引起的干扰也能分为一个周期性干扰和一个非周期性干扰。因此，采用复合控制能够对这些干扰起到补偿效果。

将式(7)改写为

(14)

图2　周期性干扰的跟踪Fig.2　The tracking of periodic disturbance

如果取式(12)所示的静态控制器，可见复合控制的引入消除了参数摄动影响，而且未改变系统的结构，仅需满足标称系统的稳定性就能保证整个系统的稳定性。综上可得，采用预测控制与H∞控制结合，并考虑采用PI控制与重复控制构成的复合控制对参数摄动、死区效用进行补偿后的系统的占空比计算式为

(15)

式中，Δyd、Δyq为ΔAX的dq轴上的展开项。

4　仿真及实验验证

为了验证本文所提设计方法的有效性，采用Matlab搭建的仿真平台进行验证。APF侧电气参数的实际值为R=0.25 Ω、L=3.1 mH，计算采用的标称值为R=0.25 Ω、L=3.4 mH，用来模拟参数摄动的影响。负载侧：Lx=1.26 mH，非线性负荷分两组，均为三相不控整流桥带阻感负载，其中R=20 Ω、L=10 mH，用以模拟外界突加负载干扰。

图3是在仅对检测部分进行两步预测时，对不同干扰抑制度补偿后电网A相电流的波形。结合表1易看出，控制增益取值越小，稳定裕度越大，但干扰抑制能力越差。APF系统在几乎变成开环系统时，补偿效果最好。

表2为在不同干扰抑制度下APF补偿后的THD，与图2一致，并能看出在该负载下补偿效果并未达到国标要求，谐波总畸变率THD超过5%。

图3　不同干扰抑制度补偿后电网A相电流Fig.3　The phase A current after compensation under different degrees of interference suppression表2　不同干扰抑制度下的THDTab.2　The THD under different degrees of interference suppression

干扰抑制度γ控制增益kTHD(%)14.364510.54101.80757.691000.26245.4312000.02305.1014000.01955.10

为了验证本文所提方法的有效性，选取控制参数：直流侧电压控制kp=2、ki=0.03，预测控制参数λd=λq=10.2，复合控制KP=1.3、Ki=0.03，闭环控制中k=17.307 3(γ=0.3时由LMI求得)。仿真结果如图4所示。由图4a可以看出本文设计的反馈校正预测控制能够很好地预测APF输出电流两步后的值，误差较小；图4b、图4c显示了在突加负载干扰下系统仍能保持稳定运行，直流侧电压基本稳定，内层控制PWM占空比计算值也未进入饱和区；从图4d中能够看出补偿后电网侧电流畸变得到了很好的改善，波形几乎为标准正弦波。表3为采用本文所提改进方法与图3中所示时滞不确定模型下γ=1 400时，补偿后各次谐波含有率的对比，本文所提方法在各次谐波的补偿尤其是高次谐波上和总THD上有明显优势。

图4　本文方法仿真结果Fig.4　The simulation results of the method in this paper表3　补偿前后谐波含有率对比Tab.3　The harmonic ratio comparison between before and after compensation

谐波次数补偿前(%)γ=1400时(%)本文方法(%)521.084.090.6976.851.720.88113.51.820.31132.831.120.46171.430.780.09190.660.540.11230.590.510.31250.650.380.13THD22.705.102.08

为了进一步说明本文方法的有效性，对表3中两种方法设计了对比实验。实验中APF采用双DSP结构，由VC33进行负载电流检测和目标补偿电流计算，由F2812进行PWM控制，采用一块双口RAM协调两片DSP的数据存取。实验中系统侧参数和控制参数均与仿真中一致，负载是电解性负载，其大小与电解液的浓度有关。在较短的一段时间内，可以看做负载在某一定值附近有小的波动。

所取得的实验结果如图5和图6所示，虽然由于电解性负载是变化的，两次实验中负载略有不同，但仍能看出采用本文改进方法补偿后的电流侧电流畸变更小，更接近于正弦波。表4为补偿后的谐波含有率，与图5、图6中所示一致。

图5　采用本文改进方法实验波形Fig.5　The experiment result of the method in this paper

图6　采用时滞鲁棒控制方法实验波形Fig.6　The experiment result of the method for literature表4　实验中补偿前后谐波含有率对比Tab.4　The harmonic ratio comparison between before and after compensation in experiment

谐波次数补偿前(%)γ=1400时(%)本文方法(%)521.084.730.9176.852.141.81113.51.170.43132.831.060.31171.430.890.29190.660.620.19230.590.430.26THD22.705.612.73

5　结论

本文采用时滞鲁棒理论对APF系统进行分析得出：时滞效应的影响造成APF对频率较高的谐波的补偿能力较差，同时造成APF在轻载情况下整体补偿效果难以达到国标要求。

给出了预测控制、H∞控制、PI控制与重复控制构成的复合控制相结合的综合控制策略及其稳定性的证明方法。相对于传统的设计方法，由于PI控制与重复控制构成的复合控制仅用来对稳态误差进行跟踪，使得重复控制增益可取值为1，提高了跟踪精度且不会影响稳定性。

仿真和实验结果证明，该方法较好地克服了时滞的影响，提高了APF对各次谐波的补偿精度，且在轻载情况下的补偿精度仍较好。

[1]张振环，刘会金，李琼林，等.基于欧拉-拉格朗日模型的单相有源电力滤波器无源性控制新方法[J].中国电机工程学报，2008，28(9)：37-44.

Zhang Zhenhuan，Liu Huijin，Li Qionglin，et al.A novel passivity-based control algorithm for single phase active power filter using euler-lagrange model[J].Proceedings of the CSEE，2008，28(9)：37-44.

[2]薛花，姜建国.基于无源性的并联型有源电力滤波器控制策略[J].电力系统自动化，2006，30(22)：12-15.Xue Hua，Jiang Jianguo.Passivity-based control strategies of shunt active power filter[J].Automation of Electric Power Systems，2006，30(22)：12-15.

[3]张振环，刘会金.单相有源电力滤波器L2增益重复控制新方法[J].中国电机工程学报，2008，28(12)：79-87.

Zhang Zhenhuan，Liu Huijin.A novel L2-gain repetitive control algorithm for single-phase active power filter[J].Proceedings of the CSEE，2008，28(12)：79-87.

[4]张振环，刘会金，张全明，等.基于PCH模型的有源电力滤波器滑动耗散阻尼限幅自适应L2增益控制[J].电工技术学报，2008，23(3)：80-91.

Zhang Zhenhuan，Liu Huijin，Zhang Quanming，et al.A novel adaptive L2-gain control algorithm with sliding dissipative damping and limitation for active power filter based on PCH model[J].Transactions of China Electrotechnical Society，2008，23(3)：80-91.

[5]魏艳迪，张勇，程新功.基于李亚普诺夫函数的三相有源电力滤波器控制策略[J].电力自动化设备，2012，32(1)：107-111.

Wei Yandi，Zhang Yong，Cheng Xingong.Control strategy for three-phase APF based on Lyapunov function[J].Electric Power Automation Equipment，2012，32(1)：107-111.

[6]李兰芳，杨洪耕，郭卫明，等.基于李亚普诺夫方法的有源电力滤波器电流稳定控制[J].电工技术学报，2012，27(9)：78-87.

Li Lanfang，Yang Honggeng，Guo Weiming，et al.Lyapunov-based current stability control method of active power filter[J].Transactions of China Electrotechnical Society，2012，27(9)：78-87.

[7]侯世英，曾建兴，孙韬，等.基于李亚普诺夫稳定性分析的APF新型控制策略[J].电力自动化设备，2010，30(10)：33-37.

Hou Shiying，Zeng Jianxing，Sun Tao，et al.APF control strategy based on Lyapunov stability analysis[J].Electric Power Automation Equipment，2010，30(10)：33-37.

[8]徐金福，张振环，刘会金，等.基于双环控制思路的有源电力滤波器H∞控制[J].电力自动化设备，2009，29(12)：41-47.

Xu Jinfu，Zhang Zhenhuan，Liu Huijin，et al.H∞ control stategy of active power filter based on dual-loop theory[J].Electric Power Automation Equipment，2009，29(12)：41-47.

[9]齐虹，林瑞全.具有控制器参数摄动的并联型有源电力滤波器H∞控制器设计[J].电力自动化设备，2010，30(1)：58-62.

Qi Hong，Lin Ruiquan.H∞ controller with parameter variation for shunt APF[J].Electric Power Automation Equipment，2010，30(1)：58-62.

[10]漆铭钧，罗安，刘定国，等.有源电力滤波器参考电流的预测方法及其实现[J].中国电机工程学报，2009，29(7)：128-134.

Qi Mingjun，Luo An，Liu Dingguo，et al.Prediction of the reference current of active power filter and its realization[J].Proceedings of the CSEE，2009，29(7)：128-134.

[11]刘元德.电力工业国家标准选编[M].北京：中国电力出版社，2004：59-70.

[12]刘宏超，吕胜民，张春晖.三相四开关并联型有源电力滤波器的SVPWM调制算法[J].电工技术学报，2011，26(4)：128-133.

Liu Hongchao，Lü Shengmin，Zhang Chunhui.Space vector pulse width modulation of three-phase four-switch shunt active power filter[J].Transactions of China Electrotechnical Society，2011，26(4)：128-133.

[13]李玉梅，马伟明.无差拍控制在串联电力有源滤波器中的应用[J].电力系统自动化，2001，16(4)：28-32.

Li Yumei，Ma Weiming.Application of deadbeat control in series active power filter[J].Automation of Electric System，2001，16(4)：28-32.

[14]杨勇，阮毅，叶斌英，等.三相并网逆变器无差拍电流预测控制方法[J].中国电机工程学报，2009，29(33)：40-46.

Yang Yong，Ruan Yi，Ye Binying，et al.Deadbeat predictive current control method for three-phase grid-connected inverters[J].Proceedings of the CSEE，2009，29(33)：40-46.

[15]牛里，杨明，刘可述，等.永磁同步电机电流预测控制算法[J].中国电机工程学报，2012，32(6)：131-137.

Niu Li，Yang Ming，Liu Keshu，et al.A predictive current control scheme for permanent magnet synchronous motors[J].Proceedings of the CSEE，2012，32(6)：131-137.

[16]王伟华，肖曦，丁有爽.永磁同步电机改进电流预测控制[J].电工技术学报，2013，28(3)：50-55.

Wang Weihua，Xiao Xi，Ding Youshuang.An improved predictive current control method for permanent magnet synchronous motors[J].Transactions of China Electrotechnical Society，2013，28(3)：50-55.

[17]贾英民.鲁棒H∞控制[M].北京：科学出版社，2007：144-176.

[18]武健，何娜，徐殿国.重复控制在并联有源滤波器中的应用[J].中国电机工程学报，2008，28(18)：66-72.

Wu Jian，He Na，Xu Dianguo.Application of repetitive control technique in shunt active power filter[J].Proceedings of the CSEE，2008，28(18)：66-72.

[19]宫金武，查晓明，陈佰锋.一种快速重复控制策略在APF中的实现和分析[J].电工技术学报，2011，26(10)：110-117.

Gong Jinwu，Zha Xiaoming，Chen Baifeng.Analysis and realization of a fast repetitive controller in active power filter system[J].Transactions of China Electrotechnical Society，2011，26(10)：110-117.

Active Power Filter Design Based on Predictive Control and H∞ Control

Ma XingLiu HuijinCui XueGuo XiaoyunWang Wenda

(School of Electrical EngineeringWuhan UniversityWuhan430072China)

In order to analyze the active power filter (APF) system more accurately，a time-delay uncertainty model for APF is designed with the consideration of time-delay，parameter perturbation，and dead band.According to the model，the time-delay H∞ robust control strategy is applied.It shows that the system robust stability and the interference suppression performance is contradictory which affects the compensation effect of the APF.So the predictive control is embedded to get the uncertainty new model of APF without time-delay and the controller is designed by H∞ control strategy to ensure the stability of the whole system.Then，a compound control strategy containing the proportion-integral (PI) control strategy and the repetitive control strategy is used to eliminate the effects of parameter perturbation which causes periodic state variables’ disturbance.Finally，Matlab simulation and physical experiments are carried out to verify the effectiveness and the correctness of the proposed method of this paper.

Active power filter，time-delay system，predictive control，H∞ control，repetitive control

2015-01-18改稿日期2015-09-18

TM712

马兴男，1987年生，博士研究生，研究方向为电能质量分析与控制。

E-mail：maxing1987@126.com

崔雪女，1974年生，副教授，硕士生导师，研究方向为电能质量分析与控制、新能源并网检测与评估、电力市场。

E-mail：g4306@sina.com(通信作者)

国家自然科学基金资助项目(51177112)。