冻滴微物理过程的分档数值模拟试验研究

徐戈 孙继明 牛生杰 周碧 王永庆



冻滴微物理过程的分档数值模拟试验研究

徐戈1, 2孙继明2, 1牛生杰1周碧3王永庆2

1南京信息工程大学大气物理学院气象灾害预报预警与评估协同创新中心，南京210044;2中国科学院大气物理研究所云降水物理与强风暴实验室，北京100029;3湖南省气象科学研究所气象防灾减灾湖南省重点实验室，长沙410118

霰和冻滴是深对流降水的主要来源。由于二者密度差异造成的不同下落末速度必然会导致云微物理过程的变化以及降水时空分布的改变。我们在以色列特拉维夫大学二维轴对称对流云全分档模式的基础上，将水成物粒子从34档增加到40档，修改了霰和雪的密度，加入冻滴分档处理的微物理过程，发展了一个包括液滴、冰晶、雪、霰和冻滴更为详细的云微物理分档模式。利用改进后的模式模拟了一次理想的强对流天气过程，分析了改进模式与原模式模拟的云微物理量场以及水成物粒子的时空分布特征，模拟结果表明：（1）由于冻滴的产生，较大的下落末速度导致在云内−3°C至−8°C较早地出现了冻滴，并造成了大量的冰晶繁生。（2）冻滴形成前期，液态水中心区域位于垂直上升速度大值中心上方，形成液态水累积区；冻滴形成期，液态水累积区位于0°C层以上，雨滴冻结生成冻滴，霰与半径大于100 μm的液滴碰并生成冻滴；冻滴增长期，在垂直上升气流的支撑下，冻滴碰并过冷水增长，导致冻滴含量增大，液态水含量减小。因此，改进模式能较好的模拟冻滴的形成过程，可以将该分档处理的微物理方案耦合到三维WRF（Weather Research and Forecasting model）模式中，更深入地研究强雷暴风切变在冰雹生成过程中的作用。

对流云 冻滴 分档模式

1 引言

冻滴是指直径小于5 mm且密度大于霰粒子的固态降水，普遍存在于深对流系统中（Braham Jr, 1964; Hanesiak and Stewart, 1995）。冻滴的主要来源是雨滴的冻结以及霰粒子与雨滴粒子的碰并。由于霰粒子和冻滴在密度上存在较大的差异，相同质量的霰粒子和冻滴具有不同的下落末速度，因此，在研究积云对流系统的微物理过程和动力过程时，需要将二者区分开来。另外一方面，冻滴和霰粒子都是冰雹粒子形成的胚胎，在强的雷暴云中，冻滴可以作为雹胚通过与液滴碰并形成冰雹粒子（盛裴轩等，2003；许焕斌，2012），因此，研究冻滴的微物理过程对于我们研究冰雹的形成也具有重要的科学意义。

对于深对流系统，由于飞机难以入云观测，很难获得对流云内部的微物理观测资料（许焕斌，1995）。云的数值模式作为对观测资料的有效补充，被广泛应用到对流云的研究和人工影响天气中。云的数值模式根据微物理过程的不同表述方式，可以分为两种，一种是参数化模式，一种是分档模式（Khain et al., 2000）。参数化模式中假定云、雨及冰粒子的谱型，利用宏观参数（如质量、密度、热量及速度等）和宏观运动学方程，描述云雨形成中微物理过程及对宏观动力过程的作用，适合于描述自然云降水粒子的总体特征，重点研究动力过程对云雾降水过程的影响。由于预报量较少，参数化模式计算起来比较节省时间，但是不适于描述粒子谱中的某尺度段粒子的演变。分档模式是将水成物粒子按尺度或质量大小划分为许多档，在积分动力过程中计算各档粒子浓度及粒子谱分布的演变，详细模拟计算云滴、雨滴及冰粒子的生长过程。这种方法对谱型未做限制，能更加详细的描述水成物粒子的演变，给予成云致雨机理更客观的解释。但分档方案因其庞大的计算量曾在使用上受到很多限制。近年来，随着大型计算机性能的大幅提高，已完全具备了云数值模式中微物理过程分档处理所需要的计算机资源。

国内外学者在分档模式方面做了大量研究。Takahashi（1976）的轴对称雹云模式中考虑了改变冰晶形状的微物理过程。Hall（1980）将冰粒子的谱划分为3类，每一类包含几个尺度档，描述冰粒子的生长特征。Sun et al.（2010, 2012a, 2012b）建立和发展了一维半非静力分档云模式，研究了气压梯度力对云滴谱演变的影响、浅对流暖云中冰晶的核化和繁生机制。Farley and Orville（1986）在冰雹分档模式中仅对雹块按质量划分为20档，分别计算各档冰雹数浓度的变化。Khain and Sednev（1996）使用含有详细微物理过程的分档云模式，考虑混合相粒子的详细分档方法，对地中海海岸的地形降水过程进行了模拟，研究其降水的成因。特拉维夫大学发展的多矩量方法可以满足分档云模式中数值计算准确性的需要。基于Tzivion et al.（1987, 1989）所采用的双矩量求解方法，Reisin et al.（1996）将该方法推广到不同种类水成物粒子之间的随机碰并和转化问题上，发展了二维轴对称非静力滞弹性对流云分档模式。Yin et al.（2000a, 2000b, 2002a, 2002b, 2005）利用该模式研究了巨核和吸湿性焰剂对对流性降水的影响，矿物性烟尘和云之间的相互作用，以及在巨核粒子作用下对流云雷达回波特征和雨滴谱的改变。徐华英等（1983）用一维非定常积云模式，研究了积云中云滴群的凝结增长，比较了几种盐核谱及不同湍流交换强度情况下凝结形成的云滴谱特征。肖辉等（1988a, 1988b）采用一维非定常积云模式，详细考虑云的微物理过程，模拟了积云发展前期云的宏、微观结构，研究了盐核谱和浓度对积云中云滴谱形成的影响，以及各种碰并过程、大气层结条件和吸湿性盐核的化学成分对积云中云滴谱形成的影响。许焕斌和段英（1999）在研究谱演变中对液相粒子群进行分档处理，通过参数化方法和分档方法的模拟对比，指出涉及粒子运动状态和人工播撒效应等过程时，应采用分档的处理方法。赵仕雄等（2004）采用分档方法研究了高原对流云降水机理中液、冰相粒子群及两者之间的相互作用。郭学良等（2001a, 2001b）建立和发展了一个三维冰雹分档强对流云数值模式，研究了冰雹的谱型特征、冰雹的产生过程和冰雹的循环增长机制。刘晓莉（2007）、刘晓莉和牛生杰（2007, 2009）在三维完全弹性冰雹云数值模式动力框架中引入分档处理的微物理过程，模拟结果与参数化模式进行对比，结果表明分档模式的模拟结果更接近实测。

在国际上，大多数分档模式没有考虑冻滴和冰雹（Morrison and Grabowski, 2010），但也出现了考虑冻滴和冰雹的分档云模式，即Hebrew University Cloud Model（HUCM）（Khain et al., 2004）。利用HUCM模式，大量学者对深对流系统进行了大量的模拟研究（Kumjian et al., 2012; Sato et al., 2012; Ryzhkov et al., 2013; Phillips et al., 2015）。然而，该模式在计算水成物并合时，是基于Bott（1998）的碰撞模型，特拉维夫大学二维轴对称模式（Yin et al., 2000a）在处理粒子碰并时是基于Tzivion的模型（1987, 1989）。通过我们的对比分析，Tzivion的模型更接近于解析解，因此，我们在特拉维夫大学二维轴对称模式的基础上，将水成物粒子从34档增加到40档，修改了雪和霰的密度，加入了冻滴的微物理过程，研究了冻滴的形成过程及其对云微物理过程的影响。我们最终的目的是将该物理模型耦合到WRF模式（Weather Research and Forecasting model）的三维动力框架下，建立一个包含液滴、冰晶、雪、霰、冻滴和冰雹的全分档对流云模式，进行冻滴和冰雹形成机制的微物理学和动力学的研究。

本文旨在建立一个包括液滴、冰晶、雪、霰和冻滴的分档云模式。利用改进模式模拟了一次理想的强对流天气过程，详细分析了改进模式与原模式模拟的云微物理量场以及水成物粒子的时空分布特征，初步探讨了深对流云中冻滴的微物理学机制。

2 模式介绍

2.1 模式动力过程

以色列特拉维夫大学二维轴对称对流云全分档模式采用在NASA/GSFC（National Aeronautics and Space Administration/Goddard Space Flight Center）发展的二维分档云模式的动力框架（Soong and Tao, 1980; Soong and Ogura, 1980; Tao and Simpson, 1993; Tao et al., 2003）。水平和垂直方向的风速利用涡度方程和流函数计算得出。模式中考虑了由于凝结过程对次网格动能的影响（Alheit et al., 1990）。动力方程的计算考虑了虚位温的扰动、比湿的扰动、云凝结核的浓度及各种水成物粒子的数浓度和质量浓度。

2.2 模式微物理过程

该模式从云凝结核开始模拟对流云降水粒子的演变过程（如图1）。液相的微物理过程包括云凝结核的核化、液滴的凝结和蒸发、液滴的碰并和破碎。冰相的微物理过程包括液滴冻结、冰晶核化（凝华核化、凝结冻结核化和接触核化）、冰晶繁生、冰粒子—冰粒子和冰粒子—液滴的相互作用（聚并、撞冻和凇附）、冰粒子融化及冰粒子的凝华和升华。模式还考虑了液滴和冰相粒子的沉降过程。

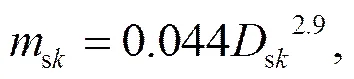
其中，m表示第档粒子的质量，ik、sk和gk分别表示冰晶、雪和霰各个档的密度，sk和gk分别表示雪和霰各个档的质量，sk和gk分别表示雪和霰各个档的直径。（3）和（5）式中和的单位分别为mg和m。

图1 模式中考虑的微物理过程示意图。实线表示相互作用的粒子种类，虚线表示相同种类粒子相互作用的过程，箭头指向粒子相互作用后产生的结果

冰相物质包括：冰晶、霰、雪花和冻滴。每种类型的粒子根据质量从34档增加到40档，每个档的质量是前一个档质量的2倍。对每个档内的粒子用质量浓度和数浓度两个矩量表示，独立考虑每档粒子与外界作用所引起的谱型变化，并利用多矩量守恒方法计算档内各类粒子的质量和浓度变化。液态和固态粒子第一档和最后一档的质量分别为0.1598×10−13kg和8.7851×110−3kg，对应液滴的直径分别为3.125 μm和25600.550 μm。冰晶、雪、霰和冻滴直径范围分别为3.238～46212.240 μm、6.017～67249.246 μm、4.085～63703.232 μm、3.237～26515.620 μm。假设冰晶为扁球形，由冰核核化形成，核化的温度范围为−20°C～−10°C（Alheit et al., 1990）。雪粒子被假设为球形并通过冰晶攀附形成。霰粒子被假设为球形，通过冰晶或雪与液滴碰并形成。假设冻滴为球形，通过半径大于80 μm的液滴冻结和霰粒子与半径大于100 μm的液滴碰并形成。改进模式中，冻滴的密度假设为0.9 g cm−3。冰晶密度由（1）式计算得出，变化范围为0.17～0.93 g cm−3，如图2（a）所示。雪的密度由（2）、（3）、（4）式求出（Locatelli and Hobbs, 1974），变化范围为0.06～0.14g cm−3（原模式中雪粒子的密度为0.2 g cm−3），如图2b所示。霰的密度由（2）、（5）、（6）式求出（Locatelli and Hobbs, 1974），变化范围为0.06～0.45g cm−3（原模式中霰粒子的密度假设为0.4g cm−3），如图2c所示。

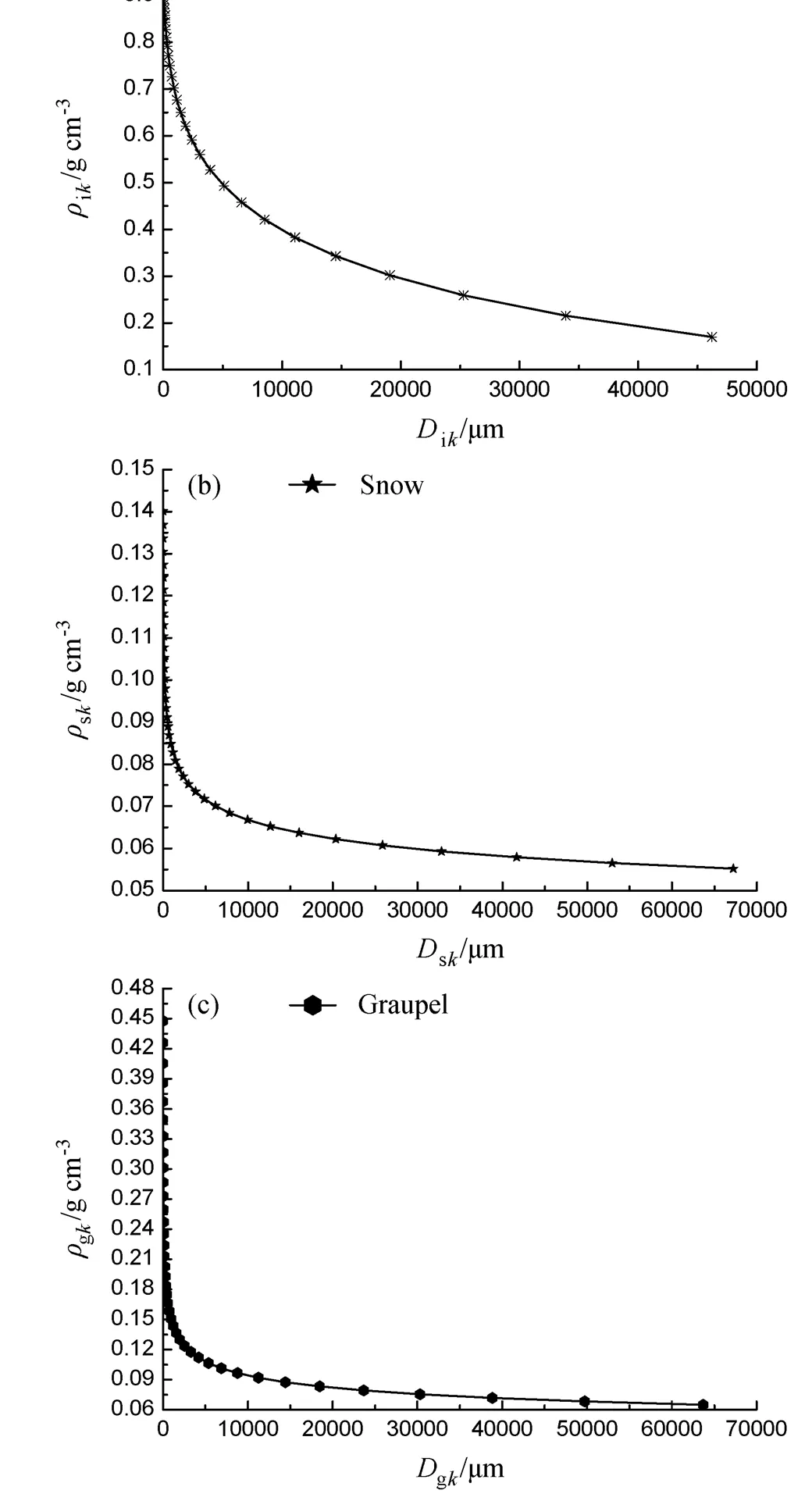
图2 （a）冰晶、（b）雪和（c）霰的密度—直径图

粒子尺度谱分布函数随时间变化方程为

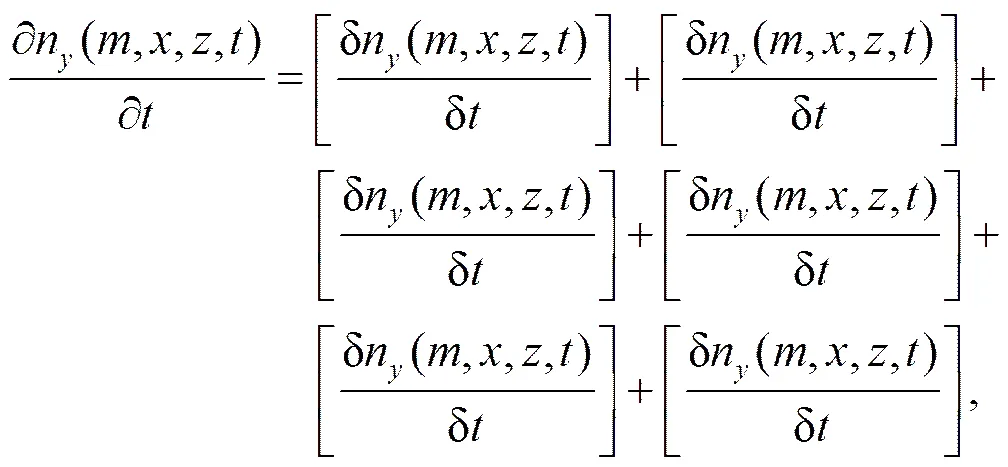
其中，n(,,,) 指水成物粒子为液滴（w）、霰（g）、冻滴（h）、冰晶（i）、雪花（s）的尺度谱分布函数，、、和分别表示水成物粒子的质量、水平距离、垂直高度和时间。公式（7）等号右侧各项依次表示液滴和冰粒子核化、液滴（冰粒子）的凝结/蒸发（凝华/升华）、粒子之间的相互作用和液滴破碎、粒子沉降、液滴冻结、冰粒子融化的随机方程。

2.3 云凝结核的核化

模式中计算的水面过饱和度大于Köhler方程计算的过饱和度时，云凝结核核化。Köhler方程为

其中，

其中，为溶质分子离解时产生的离子数：例如，NaCl（氯化钠），2；(NH4)2SO4（硫酸铵），3。为溶液滴的表面张力。为气溶胶粒子中可溶物质所占的比例。N和W分别为云凝结核和水分子的摩尔质量。S为水溶液的渗透系数。N和W分别为云凝结核和水的密度。和N分别为液滴和云凝结核的半径。v为气体常数，为温度。模式中采用Kogan（1991）的云凝结核活化方案，气溶胶谱按液滴粒子的分档方式分为64档，最小半径为0.0041 μm。

2.4 冰核核化

冰粒子的核化过程参考Meyers et al.（1992）的方案，核化机制为凝华核化、凝结冻结核化和接触核化，冰核的核化方程与相对冰面过饱和度及温度有关：

2.5 液滴冻结

模式中冰相粒子可通过冰核核化产生，也可通过液滴冻结产生。根据Bigg（1953）方案，单位时间液滴冻结生成的冰相粒子是液滴粒子数浓度w(,)、质量以及降温率的函数：

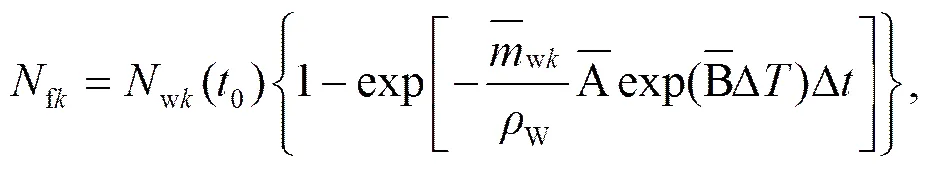
其中，wk表示第档的液滴粒子数，0表示液滴冻结的初始时刻，表示液滴冻结生成第档冻滴的平均质量。模式中液滴冻结生成冰晶和冻滴（Benmoshe et al., 2012），其中半径大于80 μm的液滴冻结产生冻滴，半径小于80 μm的液滴冻结产生冰晶，并按质量将其分配到对应的档位间隔内。

2.6 液滴凝结/蒸发与冰粒子凝华/升华

根据Tzivion et al.（1987, 1989）的方法对液滴和冰粒子的扩散增长和蒸发过程进行处理。冰、液相粒子的凝结/蒸发、凝华/升华过程的随机方程为

单个粒子的凝结/蒸发、凝华/升华后引起的质量变化方程为

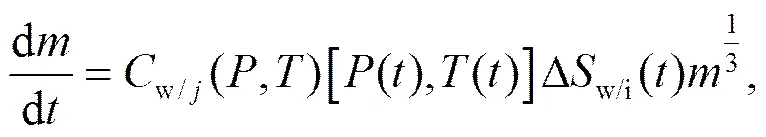
其中，Dw/i分别是相对液面和冰面过饱和度，为压强，w(,) 和C(,)（Pruppacher and Klett, 1997）是液滴（w）和冰粒子（=g, h, i, s）的和的已知函数，假设和在一个时间步长内保持恒定，则

其中，s,w为液滴的饱和比湿，为凝结潜热，a为空气热导率，Rv为水汽的比气体常数，v为水汽分子扩散系数，sat,w为液面饱和水汽压，esat,i为冰面饱和水汽压，vi为升华潜热，为冰粒子的形状因子，液滴v,w和冰粒子v,p（=g, i, s）的通风因子方程为

其中，Re为雷诺数，Sc为施密特数。冻滴的通风因子v,h参考Cheng et al.（2014）的研究成果，计算公式为

面过饱和度，Di表示冰面过饱和度，则+D时每档粒子质量和数浓度为

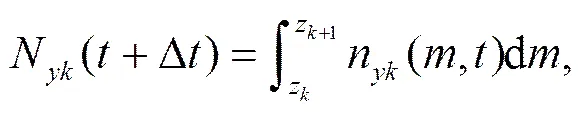
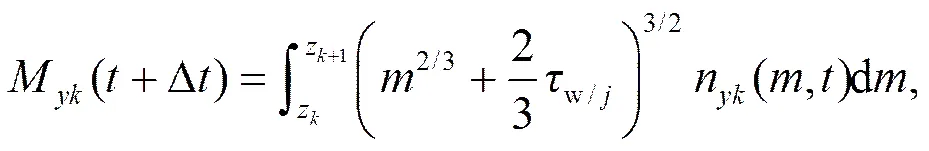
其中，

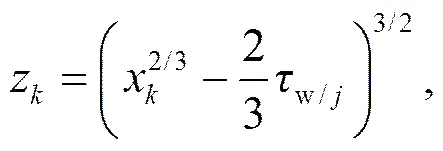
为了计算w/j，Dw和Di每个时间步长的积分为

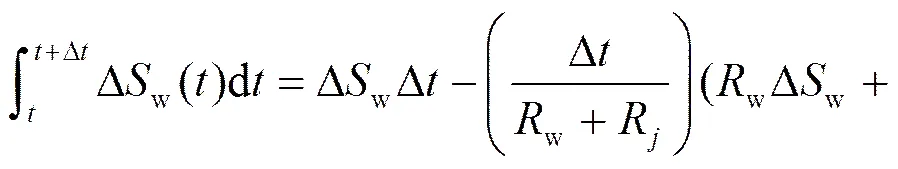
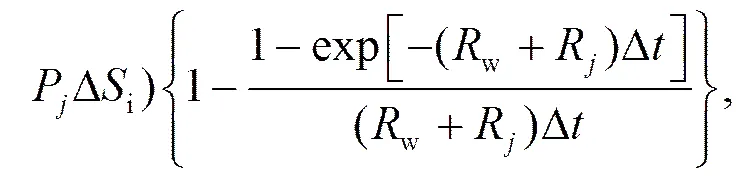
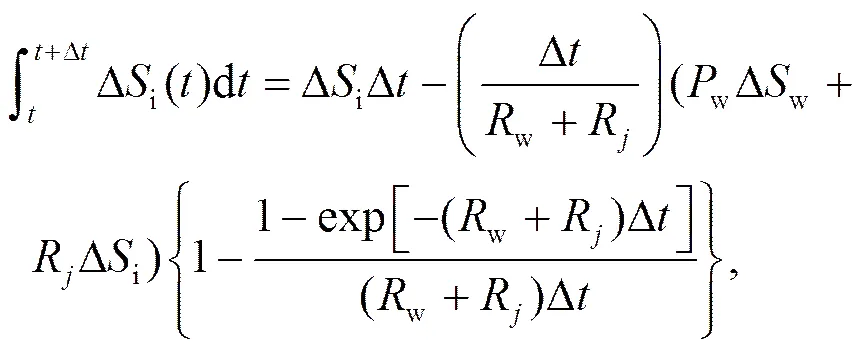
式中，

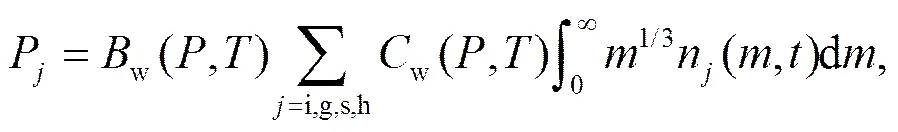
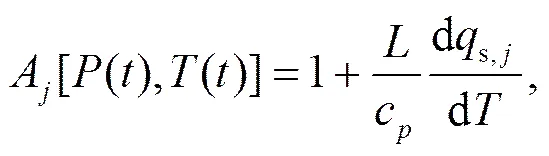
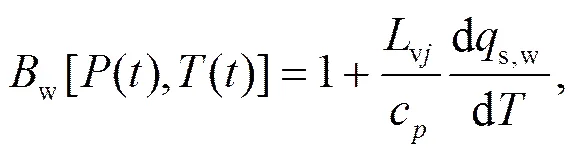
其中，c为质量定压比热容。当没有冰粒子存在时R和P为0。

冰面过饱和度Di和水面过饱和度Dw在每个时间步长因凝华/凝结、升华/蒸发过程变化，计算公式为

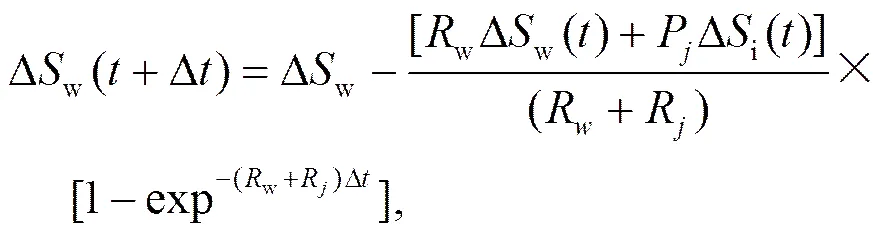
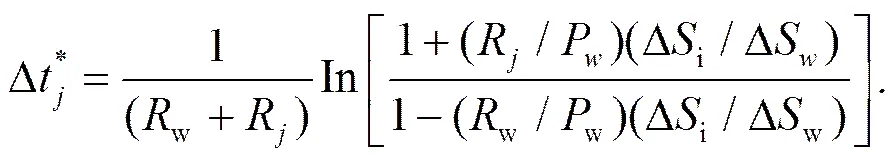
当液滴与冰粒子共存时，若环境水汽压大于水面饱和水汽压，粒子凝华/凝结增长，随着环境水汽压逐渐减小，直到其小于水面饱和水汽压大于冰面饱和水汽压时，冰粒子继续凝华增长，液滴粒子开始蒸发（Bergeron过程）。因此，需要计算一个时间步长内将液滴粒子由凝结状态转变为蒸发状态。当Dw＞0，首先计算当Dw=0时，的值。再与模式中处理微物理过程的时间间隔D比较：若，表明在一个时间步长内没有凝结和蒸发过程的转换，D仍作为计算微物理过程的时间步长；若，则一个时间步长内液滴粒子需计算两个过程，用来计算液滴和冰粒子的凝结/凝华过程，计算液滴的蒸发过程。同样的方法用来处理冰粒子凝华/升华过程的转换。

图3 云滴碰并增长10分钟后滴谱分布，云滴谱共34档

凝结/凝华和蒸发/升华的计算过程为：首先计算一个积分间隔z和z1，该档内的所有粒子在D时刻完全落入x和x1；然后对时刻间隔z和z1内的粒子谱型积分；最后对x和x1内的矩量进行更新，从而实现粒子谱型改变。每个时间步长内的粒子谱为

由于无法确定水凝物里凝结核的数量、尺度和种类，因此不能确定蒸发后释放粒子的种类。该模式不考虑云凝结核和冰核的循环。

2.7 冰粒子融化

在冰相粒子的融化过程中，冰粒子融化吸收环境热量使空气冷却，浮力减小，产生下沉气流，抑制云的持续发展；冰粒子密度发生变化，影响其通风系数和沉降速率，进而改变云内的动力过程；同时，融化后产生的小液滴在气流作用下从冰粒子表面移走，影响粒子的碰并系数，使粒子谱型发生变化。因此，冰粒子的融化过程非常重要。当液滴与冰粒子共存时，假设冰粒子在环境温度大于0°C时立即融化并全部转化为液滴（Khvorostyanov et al., 1989），或是根据冰粒子的沉降速率假定其在0°C层下一定距离内完全融化（Takahashi, 1976）。

模式中融化过程的处理类似于蒸发过程。冰粒子的融化方程为

其中，n(,)指冰相粒子为霰（g）、冻滴（h）、冰晶（i）、雪花（s）的尺度谱分布函数。

单个粒子融化方程为

式中，(,)（Rasmussen and Heymsfield, 1987）定义为压强和温度的函数，表示为

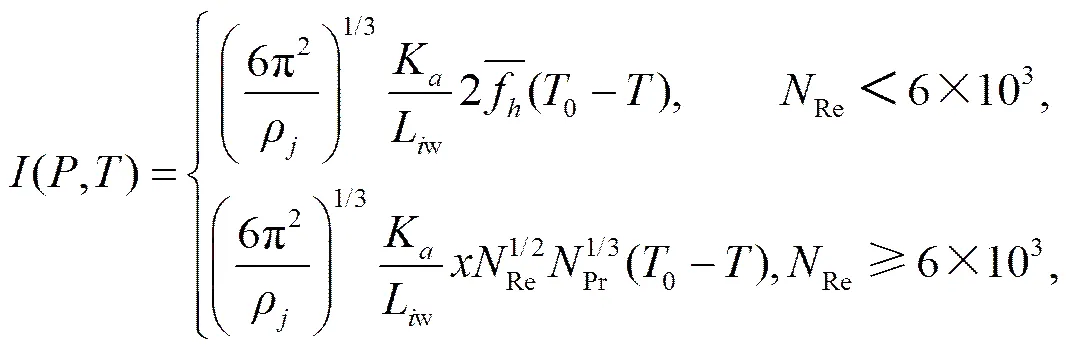
其中，K和Pr分别为热扩散系数和普朗特数，iw为融化潜热，为冰相粒子霰（g）、冻滴（h）、冰晶（i）、雪花（s）的密度，f为通风系数：

当Re≤2×10−4，=0.74；否则=0.57+92×10−6Re。

假设在一个时间步长中温度为常数，粒子融化经历D时间后谱型为

假设一个时间步长内冰粒子融化后产生液态水在气流作用下从冰粒子表面移出，被分为质量相等的两个液滴粒子，归入与其质量相对应的液滴档内。

2.8 不同相态粒子之间的随机碰并及雨滴破碎

该模式考虑了液滴、冰晶、霰、雪和冻滴之间的碰并及雨滴的碰撞破碎（Low and List, 1982a, 1982b），不同粒子相互转化遵循以下基本规则：

（1）雪粒子只由冰晶攀附粘连产生（即冰晶聚合体）；

（2）冰晶通过淞附质量小于自身质量的液滴增长，当淞附的总质量大于自身质量时转化为霰；

（3）雨滴与小于自身质量的雪和冰晶碰撞生成霰；

（4）霰与半径大于100 μm的液滴碰撞后转化为冻滴，否则转化为霰；

（5）霰/冻滴与其他种类粒子相互作用总是产生是霰/冻滴。

采用Tzivion et al.（1987, 1989）与Feingold et al.（1988）求解液相粒子随机碰并方程的数值解法求解碰并方程。图3为云滴经过10分钟的碰并增长后的谱分布。从图3可以看出如果采用Bott（1998）的数值算法，得到的误差较大。因此，我们选取了Tzivion et al.（1987, 1989）的碰并模型。由于不同粒子之间相互作用后可能改变自身的特性（如密度），并被分配到其他种类粒子的对应档内，因此要考虑不同种类粒子之间的相互转化。

不同粒子之间的随机碰并数浓度方程为

其中，n(,,,)指水成物粒子为液滴（w）、霰（g）、冻滴（h）、冰晶（i）、雪花（s）的尺度谱分布函数（1、2），函数1, y2用来选择粒子增加项的相互作用，函数w用来选择液滴粒子增加项的相互作用，n1(−x,,,)表示在时刻（,）位置质量为（−x）的水成物粒子1的尺度谱分布函数，n2（x,,,）表示在时刻（,）位置质量为x的水成物粒子2的尺度谱分布函数，n(x,,,)表示在时刻（,）位置质量为x的水成物粒子*的尺度谱分布函数，n(x,,,)表示在时刻（,）位置质量为x的液滴粒子的尺度谱分布函数，n(y,,,)表示在时刻（,）位置质量为y的液滴粒子的尺度谱分布函数(x+y=m)，n(,,)表示在时刻（,）位置质量为的液滴粒子的尺度谱分布函数，C1, y2(−x, x)表示质量分别为（−x）和x的粒子1和2的收集核函数，C, y*(, x)表示质量分别为和x的粒子和*的收集核函数，(x,y)表示质量分别为x和y液滴的碰并破碎核函数，(;x,y)为和y碰撞导致的质量为的液滴碎片的分布函数，(x;,y)为和y碰撞导致的质量为x的液滴碎片的分布函数。上式右边各项分别表示为

（1）质量为的粒子源项，表示质量分别为和−x的粒子相互碰撞并合；

（2）质量为的粒子汇项，表示质量为的粒子与其他粒子碰并所造成的损失；

（3）液滴粒子碰并破碎项，表示质量为的粒子因碰并破碎引起的增加；

（4）液滴粒子碰并破碎项，表示质量为的粒子因碰并破碎引起的减少。

质量分别为和的粒子和的收集核函数C, b(,)和碰并破碎核函数(x,y)分别定义为

其中，K, b(,)为质量分别为和的粒子和的重力收集核函数，E, b(,)为其碰并效率，w, w(x,y)和w, w(x,y)分别表示液滴与液滴的重力收集核函数及其碰并效率。模式中不同尺度不同种类粒子之间的碰并系数参考以前学者的研究成果：（1）雨滴的碰并系数，当＜0.1时，参考Long（1974）的研究结果；当0.1＜＜0.6时，参考Ochs III et al.（1986）的研究结果；当＞0.6时，参考Low and List（1982a, 1982b）的研究结果。（2）液滴与冰晶的碰并系数参考Martin et al.（1981）和Lew et al.（1985）的研究结果。（3）液滴和霰/冻滴的碰并系数参考Hall（1980）、Rasmussen and Heymsfield（1985）的研究成果。（4）Wang and Chang（1993）给出了其他粒子之间的碰并系数。由于实验条件的限制，以上碰并系数只在很小的尺度区间有效，并不涵盖水成物粒子的整个尺度区间。因此，参考Chen（1992）的方法拓宽碰并系数，使其覆盖水成物粒子的整个尺度区间，使碰并过程在整个尺度区间范围内进行。

2.9 冰晶繁生

Hallett-Mossop机制（Hallett and Mossop, 1974）产生次生冰晶，参考Mossop（1978）的处理方法，每个时间步长产生的次生冰晶数是大粒子数（≥24.8 μm）和被霰粒子收集的小粒子数（≤12.3 μm）的函数。考虑温度影响（Cotton et al., 1986），次生冰晶在−5°C时产生率最大。

2.10 液滴和冰粒子的沉降

因沉降过程导致粒子谱型改变的方程为

液滴下落末速度（Beard, 1977）为

冰粒子下落末速度（Böhm, 1989）为

雷诺数Re为

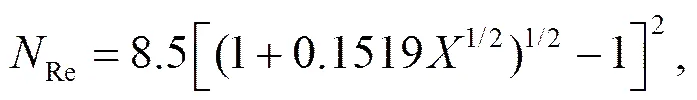
其中，

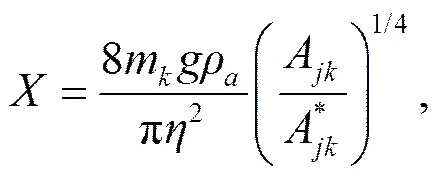
其中，A表示质量为m的粒子被气流影响的有效面积，定义为粒子空间投影区域A*的最小外切圆，为黏性系数。

由公式（51）和公式（8、9）可以获得第档内粒子数浓度N和质量浓度M的平流方程。平流方程的计算采用Smolarkiewicz（1983）的正定平流方案，使数值扩散最小化。

3 模拟结果及分析

3.1 模式的初始场

本文用温度和露点的理论廓线构造水平均匀的模式初始场（Yin et al., 2000b）。地面的温度、露点温度和压强分别为26°C、15.8°C和1007 hPa。根据地面和高空各层的气压、温度、露点、风向和风速插值并诊断出模式各层上的空气密度、无量纲气压、位温、比湿、风速分量等模式计算所需要的初始值。本文模拟区域水平尺度取100个格点，垂直取40个格点，水平和垂直格距均为300 m。模式采用的动力过程时间步长为5 s，而冰晶、雪花、霰和冻滴的升华/凝华、液滴粒子的蒸发/凝结等微物理过程的时间步长为2.5 s。整个过程模拟时间为100 min。

本文采用热泡扰动的方式激发初始对流云，即在模拟时间=0，垂直高度为600 m的水平中心处（15 km）加一温度为2°C的温度扰动场，通过垂直运动方程的浮力项来建立初始对流。模式中没有考虑风切变的影响。

3.2 云内物理量场的时间分布特征

为了研究模式中加入冻滴过程后对对流云内物理量场的影响，分别用原模式和改进模式模拟同一个理想个例，选取中心区域即水平15 km处的时间—高度剖面图，将其垂直速度场、水面和冰面饱和度场进行对比分析。

在对流云的发展阶段，云内存在上升气流。随着上升气流进入云内的水汽凝结而释放大量潜热，使云内上升气流进一步增强。在对流云的成熟阶段，云内开始出现雨、雪、霰和冻滴等降水粒子，这些降水粒子下落时将拖曳周围的空气一起下沉，云中开始出现下沉气流。在对流云的低层，当下沉气流阻碍上升气流，并最终切断上升气流的来源，云内低层均为下沉气流，对流云进入消散阶段。图4给出了垂直速度的时间—高度剖面图。如图所示，在30～ 50 min时，2～6 km的高度上出现了强的上升气流，速度大值中心位于3～5 km，达到了12 m s−1。在55 min时，4 km处有一个小范围的上升速度大值区，最大垂直速度为6 m s−1。55 min后，4 km以下的区域出现下沉气流，下沉气流的速度随时间先增大后减小，在62 min的1 km处下沉气流速度为最大，达到了8 m s−1。改进模式（图4b）与原模式（图4a）相比，变化趋势比较一致，但在40 min时，垂直上升速度最大值达到了13 m s−1；在45～55 min时3～4 km高度上垂直上升速度为6 m s−1。改进模式与原模式相比，垂直速度场的强度增加。

水面饱和度的时间—高度剖面分布如图5所示：水面饱和度均在23 min时，1.5 km以上的高度开始出现水面过饱和，有云体出现；在40 min，2.5～5.5 km的高度范围内出现了水面饱和度大值区，最大值达到104%，改进模式在3～5 km的区域内最大值为106%；60 min时3.5 km的高度上再次出现水面饱和度达到104%的大值区，改进的模式（图5b）最大值为110%；70～75 min，原模式（图5a）在4.5 km高度再次出现水面饱和度大值区，最大值为102%，小于前两次的水面饱和度，改进模式（图5b）与原模式（图5a）相比，水面过饱和范围和强度均增大，最大值为106%；80 min后，过饱和现象均消失。

图6给出了模式改进前后冰面饱和度的时间—高度剖面图。从图中可以看出：在30 min时，3 km的高度开始出现冰面过饱和的现象，冰核核化，有冰相粒子形成；随着云的发展，在40～45 min期间，5.5～6.5 km的高度范围内出现了冰面饱和度的大值区域，最大值达到了130%；在50～80 min时，再次出现两个冰面饱和度大值区，分别为125%和120%，强度依次减小。改进模式的冰面饱和度分布图（图6b）与原模式的冰面饱和度图（图6a）相比，在55 min之前，其变化和原模式（图6a）一致，同样在30 min时，3 km的高度出现冰面过饱和的现象，在40～45 min，5.5～6.5 km的高度范围内存在冰面饱和度最大值为130%的大值中心。在55～80 min期间相继出现冰面饱和度为130%和125%的大值中心。80分钟以后，改进模式的冰面饱和度大于原模式。

图5 水面饱和度的时间—高度剖面：（a）原模式；（b）改进模式

图6 冰面饱和度的时间—高度剖面：（a）原模式；（b）改进模式

3.3 云内水成物粒子浓度的时间分布特征

为了研究冻滴加入后对云内其他水成物粒子演变的影响，首先要保证我们在模式中加入冻滴的方法是正确的。为此，我们先假设冻滴的密度和下落末速度与霰粒子完全一致，这样加入前模拟的霰粒子浓度与加入后霰粒子和冻滴的和随时间分布完全一致，在此条件下，再修订冻滴的密度和下落末速度。下面是修订后，模式改进前后水成物粒子的浓度分布特征。

图7给出了模式改进前后总水成物粒子数浓度和温度的时间—高度剖面。图7a中水成物粒子包括液滴、冰晶、雪和霰四种粒子。在23 min时，1.5 km的高度层，有水成物粒子形成；在35～40 min时，3～5 km的高度层温度升高，水成物粒子浓度出现最大值（5×105L−1）；从50 min开始，温度降低，有降水产生；80 min后，对流云开始消散，降水停止。图7b中包括液滴、冰晶、雪、霰和冻滴五种水成物粒子。与图7a相比水成物粒子的分布特征及降水的演变特征基本一致，但水成物粒子数浓度在45～70 min时3～6 km的高度层，数浓度大值区范围比图7a略小，3 km以下数浓度大值区范围比图7a略大。由于霰的生成机制减少，从而霰粒子减少；有冻滴产生，冻滴通过碰并过冷水增长，消耗过冷水，导致液态水减少；冻滴密度大于霰粒子的密度，相比霰粒子具有较大的下落末速度，从而总水成物粒子浓度在高空减小，在近地面增大。

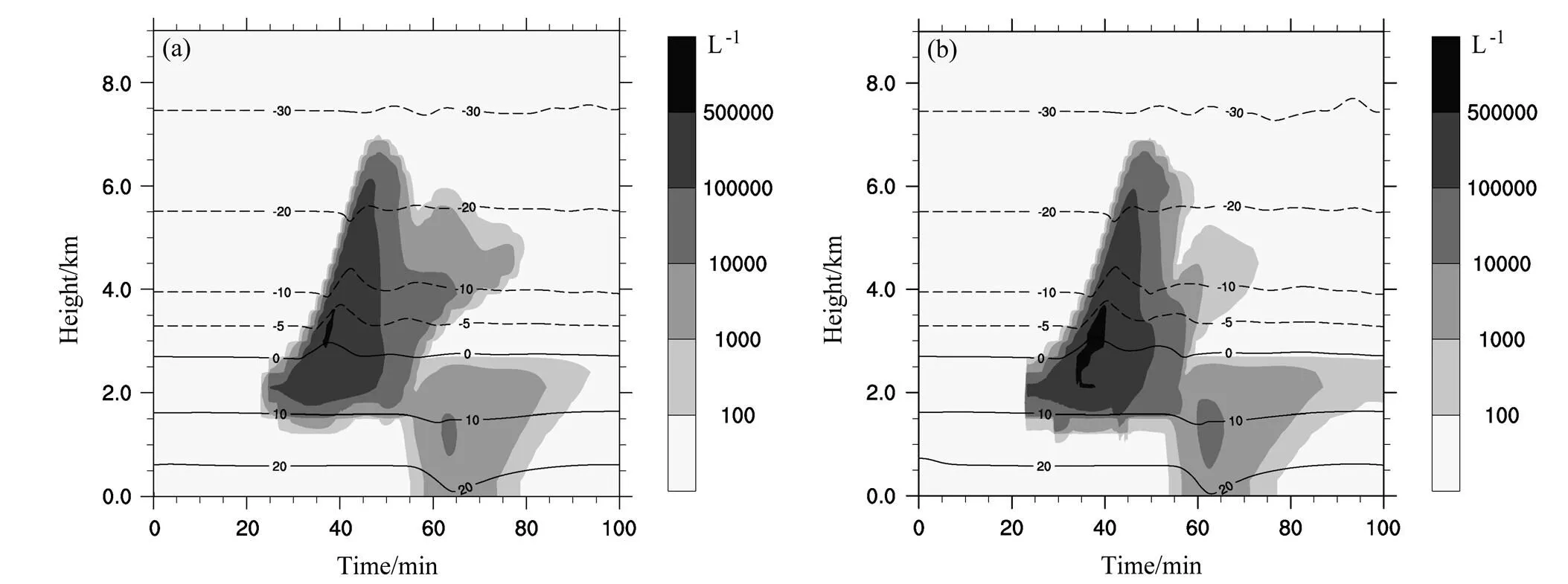
图7 总水成物粒子数浓度和温度的时间—高度剖面：（a）原模式；（b）改进模式。实（虚）线表示温度（单位：°C）的正（负）值，阴影表示粒子数浓度（单位：L−1）

图8 总水成物粒子质量浓度和温度的时间—高度剖面：（a）原模式；（b）改进模式。实（虚）线表示温度（单位：°C）的正（负）值，阴影表示总水成物粒子质量浓度（单位：g kg−1）

改进模式和原模式中水成物粒子质量浓度和温度的时间—高度演变特征基本一致，如图8所示，与图7的水成物粒子数浓度分布相对应，50～80 min为降水过程。图8a中水成物粒子质量浓度在40～60 min时出现了大值中心，最大值为4 g kg−1。图8b中水成物粒子的质量浓度在60 min时，500 m的高度层以下质量浓度比图8a大；55～65 min时2～5 km大值区域比图8a小。结合数浓度图，改进模式中有冻滴生成，冻滴碰并过冷水继续增长，冻滴密度大，降到地面使其总水成物粒子质量浓度大于原模式。

图9给出了液滴数浓度和温度的时间—高度剖面。结合水面饱和度（图5），在23 min时1.5 km的高度层，水面达到过饱和，云凝结核活化，有液滴形成；在35～40 min时，3 km的高度层液滴粒子浓度出现最大值（5×105L−1）；当55 min时，有降水产生，浓度最大为104L−1，主要是由于高层冰相粒子融化产生降水。图9b与图9a基本一致，但在35～40 min时，液滴浓度的大值区域范围较大，主要是由于该区域水面过饱和范围较大。在降水阶段，3 km的高度层以上液滴浓度大值区域较小，主要是冻滴增长消耗过冷水所导致；3 km以下液滴浓度的大值区域较大，主要是生成的冻滴具有较大的下落末速度，当液滴下落到0°C层以下融化形成降水，导致液滴数浓度增加。

图9 液滴数浓度和温度的时间—高度剖面：（a）原模式；（b）改进模式。实（虚）线表示温度（单位：°C）的正（负）值，阴影表示液滴数浓度（单位：L−1）

图10 液滴质量浓度和温度的时间—高度剖面：（a）原模式；（b）改进模式。实（虚）线表示温度（单位：°C）的正（负）值，阴影表示液滴质量浓度（单位：g kg−1）

液滴质量浓度和温度的时间—高度剖面分布如图10所示，与其数浓度分布（图9）相对应，在23 min时，1.5 km的高度层，有液滴形成；在35～50 min时，3～6 km的高度层液滴粒子质量浓度出现大值中心，最大达到5 g kg−1；55 min时，冰相粒子融化降落到地面，有降水产生，浓度最大为2 g kg−1。图10b与图10a基本一致，但在降水阶段2～5.5 km的范围内液滴质量浓度小于图10a，与数浓度分布特征一致；在85 min后的消散阶段，改进的模式的质量浓度（图10b）大于原模式（图10a），主要是由于改进模式在此阶段高空中的冰相粒子增多，随着冰相粒子的沉降作用，降落到0°C层时开始融化，因此到达地面的液相粒子增多。

图11给出了冰晶数浓度和温度的时间—高度剖面。与冰面饱和度分布（图6）相对应，在35 min时，3 km的高度层，冰面达到过饱和，冰晶核化，有冰晶形成；在45 min时，6.5 km的高度层冰晶粒子数浓度出现最大值（97 L−1）。图11b中冰晶数浓度分布与图11a基本一致，但在50～60 min时，3～5 km的高度层冰晶数浓度最大值为90 L−1，大于图11a，主要是改进模式有冻滴生成，此处是冻滴质量浓度的大值区，冻滴在该高度层上的繁生率最大，生成次生冰晶，因此冰晶粒子的数浓度增大。60 min以后的4～7 km的空间区域内冰晶数浓度大值区范围大于原模式，主要是由于该范围内改进模式中冰面饱和度大于原模式，冰核核化增多。

冰晶质量浓度如图12所示，改进模式质量浓度分布（图12b）情况与原模式（图12a）基本一致，但50～60 min时，3～5 km的高度层冰晶质量浓度大于原模式；在70 min以后的4～6 km的空间区域内，冰晶的质量浓度大值区最大为0.8 g kg−1，大于原模式中的质量浓度（0.5 g kg−1）。

图11 冰晶数浓度和温度的时间—高度剖面：（a）原模式；（b）改进模式。实（虚）线表示温度（单位：°C）的正（负）值，阴影表示冰晶数浓度（单位：L−1）

图12 冰晶质量浓度和温度的时间—高度剖面：（a）原模式；（b）改进模式。实（虚）线表示温度（单位：°C）的正（负）值，阴影表示冰晶质量浓度（单位：g kg−1）

雪数浓度和温度的时间—高度剖面分布如图13所示，由于雪粒子只由冰晶攀附粘连产生，因此雪的浓度分布情况与冰晶相对应。在40 min时5.5 km的高度层，有雪形成；在80 min时，4 km高度层上雪粒子数浓度出现最大值（0.002 L−1）。图13b中雪粒子数浓度分布与图13a相比，55 min开始雪粒子数浓度大值区范围向下扩散，与冰晶的大值区相对应，主要是由于该范围内冻滴和液滴碰撞后发生了冰晶的繁生，冰晶浓度增加，雪粒子由冰晶攀附粘连产生，因此雪粒子数浓度增加。65 min后，2.5～5.5 km范围内雪粒子的数浓度大于原模式，主要是由于该范围内冰晶粒子增多所导致。

雪质量浓度如图14所示，改进模式质量浓度分布（图14b）情况与原模式（图14a）基本一致，同样，在50 min时，5.5 km高度层上雪粒子质量浓度的大值区范围整体向下扩大，65 min后，2.5～5.5 km范围内雪粒子的质量浓度大于原模式。

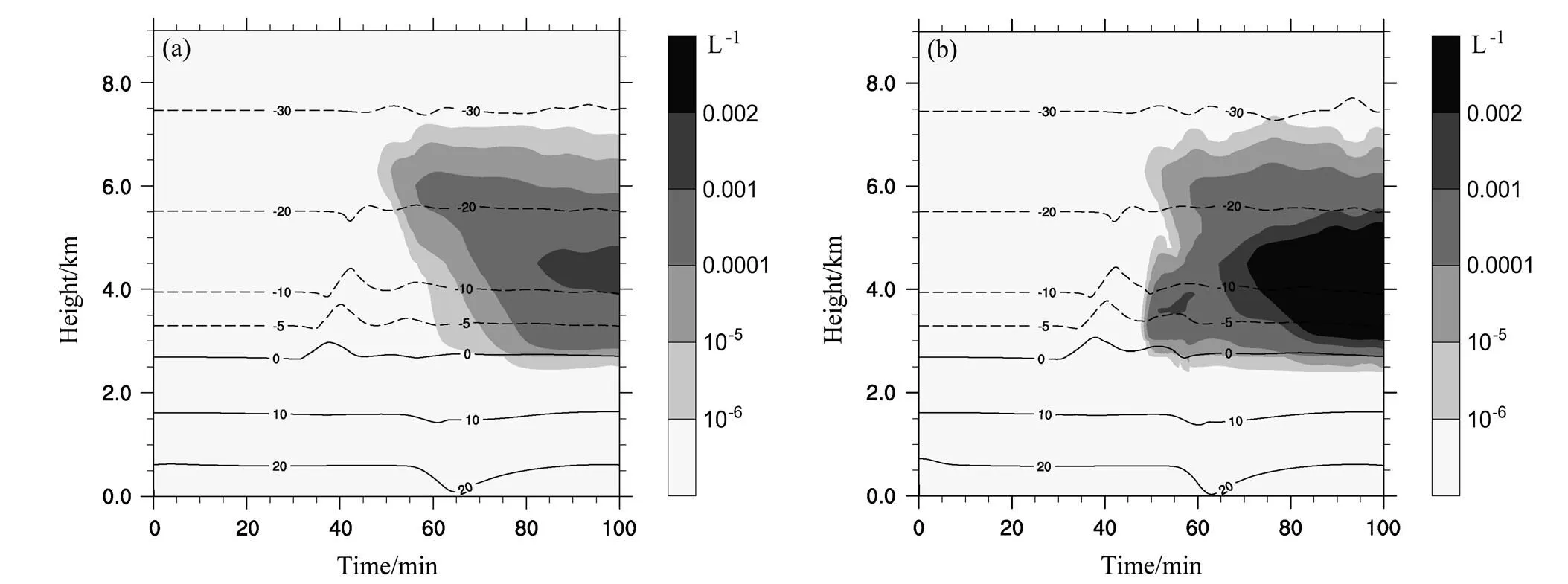
图13 雪粒子数浓度和温度的时间—高度剖面：（a）原模式；（b）改进模式。实（虚）线表示温度（单位：°C）的正（负）值，阴影表示雪粒子数浓度（单位：L−1）

图14 雪粒子质量浓度和温度的时间—高度剖面：（a）原模式；（b）改进模式。实（虚）线表示温度（单位：°C）的正（负）值，阴影表示雪粒子质量浓度（单位：g kg−1）

图15给出了霰粒子数浓度和温度的时间—高度剖面。从图中可以看出，在40 min时，在5 km的高度层，有霰粒子形成；在50 min时，6 km的高度层霰粒子浓度出现最大值（3 L−1）。图15b中霰数浓度分布与图15a一致，但霰粒子浓度最大为1 L−1且大值区范围缩小。主要是原模式中液滴冻结产生冰晶和霰的过程改为生成冻滴和冰晶；原模式假设霰与液滴碰并均转化为霰，改进的模式中将霰与半径大于100 μm的液滴碰并转化为冻滴，否则转化为霰粒子，从而霰的生成机制减少，霰粒子的数浓度也随之减小。霰质量浓度分布情况（图16）与数浓度一致，在50 min时，3～6 km的高度层改进模式（图16b）中霰的质量浓度（1 g kg−1）小于原模式（图16a）中霰的质量浓度（2 g kg−1），且大值区范围缩小。

由冰雹的微结构观测表明（许焕斌，2012），冰雹由两部分组成：一是雹胚；二是雹块。雹胚在对流云成云致雨的过程中形成。雹胚有两种：冻滴胚和霰胚。霰胚又分为雪霰胚和滴霰胚。因此，雹胚的形成方式有三种：（1）水汽凝结形成云滴，云滴经过扩散增长和碰并增长形成雨滴，雨滴冻结形成冻滴胚；（2）水汽凝华形成冰晶，冰晶继续扩散增长并攀附形成雪晶，雪晶淞附，形成雪霰胚；（3）水汽凝结形成云滴，云滴凝结增长和碰并增长形成大云滴，大云滴先冻结再经过凝华淞附增长为毫米大小的霰，形成滴霰胚，即霰淞附的核心是大的冻滴而不是雪晶。即雹胚的形成问题归纳为：雨滴的冻结和形成、可启动淞附增长的雪晶的形成和大云滴的形成，同时还要有能提供给淞附增长的过冷云滴群（过冷云水）。雹胚形成以后，在继续长成冰雹的过程中，雹块主要通过碰并云内的过冷液滴来增长，也可以在雹块表面存在水膜的情况下捕获一些冰晶或冰粒子来增长。

图15 霰数浓度和温度的时间—高度剖面：（a）原模式；（b）改进模式。实（虚）线表示温度（单位：°C）的正（负）值，阴影表示霰数浓度（单位：L−1）

图16 霰质量浓度和温度的时间—高度剖面：（a）原模式；（b）改进模式。实（虚）线表示温度（单位：°C）的正（负）值，阴影表示霰质量浓度（单位：g kg−1）

因此，为了下一步模拟冰雹的形成过程，改进模式增加了冻滴的微物理过程。冻滴主要由两个过程产生：（1）液滴冻结生成冻滴和冰晶（原模式转化为冰晶和霰）；（2）霰与半径大于100 μm的液滴碰撞转化为冻滴（原模式中假设霰与液滴碰撞均转化为霰）。同时，改进模式中还考虑了冻滴的凝华/升华、融化、与其他水成物粒子的相互作用及沉降等微物理过程。

冻滴浓度的分布情况如图17所示，图17a为冻滴的数浓度，图17b为冻滴的质量浓度。结合垂直速度（图4）和液态水含量（图10）的分布，进行分析。

在冻滴形成前期，随着对流云的发展，最大上升气流随之增大，中心位置上抬，液态水含量也逐渐增大，大值中心上移，液态水大值中心位于上升气流大值区上方。垂直上升气流和液态水的这种配置形成了液态水累积区。上升气流携带较大的液滴上升，液滴逐渐长大并穿过液态水累积区，由于该区域内液态水含量较大，液滴增长很快，液滴上升到负温度区后，冻结形成冻滴。同时，由于40 min时5 km的高度层有霰形成，随后霰与半径大于100 μm的液滴碰撞也能生成冻滴。如图所示，44 min时，在5 km的高度层，有冻滴形成。

冻滴形成后，主要靠捕获过冷水滴形成撞冻冰来增长。冻滴质量谱分布在44、47、50、53 min的演变特征如图18所示，横坐标为冻滴的直径，纵坐标为高度，均为单峰型分布。44 min时冻滴谱存在于5～6 km，冻滴直径小于1657.23 μm，质量浓度为0.001 g kg−1；47 min时，粒子直径增长至6628.91 μm，质量浓度增大至0.1 g kg−1，高度范围为3～7 km；50 min时，液滴质量浓度增大至0.4 g kg−1，谱宽增长至16703.79 μm，高度范围为0.5～7 km；53 min时，液滴质量浓度极大值仍为0.4 g kg−1，但大值区范围较50 min时有所增大，冻滴直径最大值与50 min时相同，为16703.79 μm，高度范围从地面至7 km。该过程中，由于冻滴在垂直上升气流的支撑下上升，随着云的进一步发展，云上部的上升气流较弱，当上升气流托不住长大的冻滴时，冻滴就会下落，并沿途继续与过冷水滴碰并而增长，最后返回到液态水累积区，并滞留在该区域持续增长，从而导致冻滴的含量和尺度逐渐增大。因此，冻滴的生长区位于液态水累积区。由于冻滴增长消耗过冷水，导致液态水含量的变化与冻滴恰好相反，随着冻滴含量的逐渐增大，液态水含量逐渐减小。50～60 min时间内，冻滴在0°C层以上出现了浓度的大值中心，数浓度和质量浓度的最大值分别为4 L−1和2 g kg−1。

当冻滴增长到足够大时克服上升气流，在重力作用下降落到地面。如图17所示，55～73 min期间，有冻滴降落到地面，数浓度和质量浓度最大值分别为0.1 L−1和1 g kg−1。

图17 （a）冻滴数浓度、（b）质量浓度和温度的时间—高度剖面。实（虚）线表示温度（单位：°C）的正（负）值，a图中的阴影表示冻滴数浓度（单位：L−1），b图中的阴影表示冻滴质量浓度（单位：g kg−1）

从图17中冻滴浓度的分布图可以看出，冻滴数浓度如图17a所示，大值中心位于5.5 km以上的高度层，而冻滴质量浓度的大值中心如图17b所示，主要位于3～5.5 km的高度范围，比冻滴的数浓度大值中心高度略低。然而从其他冰粒子浓度的分布情况（图11–16）可以看出，数浓度和质量浓度的大值区域位置基本一致。主要是由于不同大小、不同类型的水成物粒子的下落末速度不同所造成的。

图18 冻滴质量谱随时间的演变：（a）44 min；（b）47 min；（c）50 min；（d）53 min

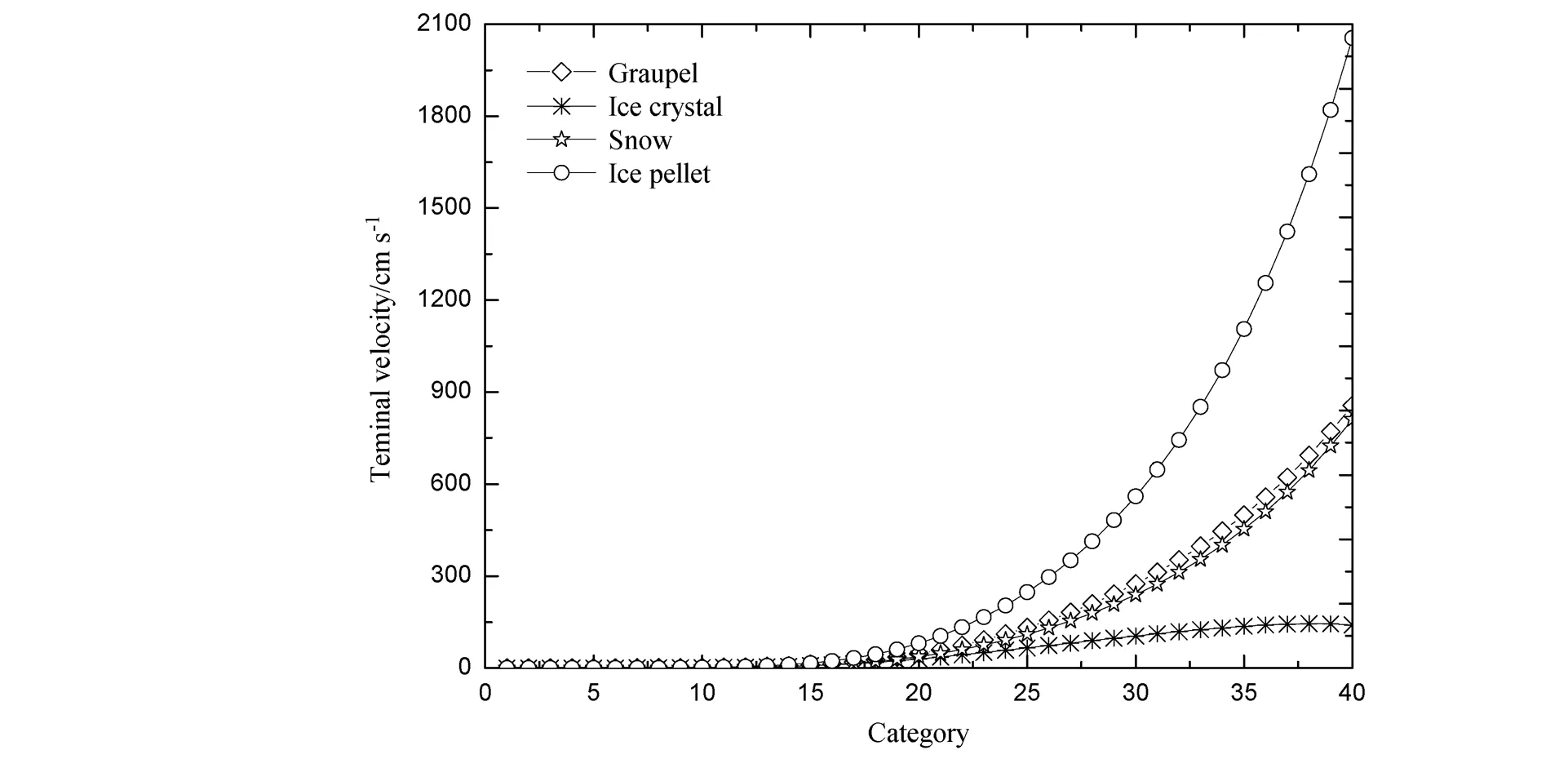
图19 四种（冰晶、雪、霰和冻滴）水成物粒子各个档的下落末速度

图19给出了冰晶、雪、霰和冻滴在各个档的下落末速度图。由公式（52）～（55）可以看出水成物粒子的下落末速度与粒子的尺度成反比关系。在同一档内，水成物粒子的质量相同，由于其密度不同，水成物粒子的尺度大小不同，水成物粒子的密度越大，则尺度越小。由于水成物粒子的密度从大到小依次为冻滴、霰、雪和冰晶。因此，在同一档内，水成物粒子半径从大到下依次为冰晶、雪、霰和冻滴，下落末速度从大到小依次为冻滴、霰、雪和冰晶。对于同种水成物粒子，密度相同时，水成物粒子的下落末速度与粒子尺度的二分之一次方成正比关系。因此，粒子尺度越大，下落末速度越大。图20给出了冻滴16～36档质量浓度和温度的时间—高度剖面，从图中可以看出，16～26档冻滴粒子的大值中心均位于5.5 km以上，而27～36档冻滴粒子的大值中心位于5.5 km以下。综上所述，低层冻滴质量浓度的大值中心是由尺度较大的冻滴下落形成的。

图20 冻滴16～36档质量浓度和温度的时间—高度剖面

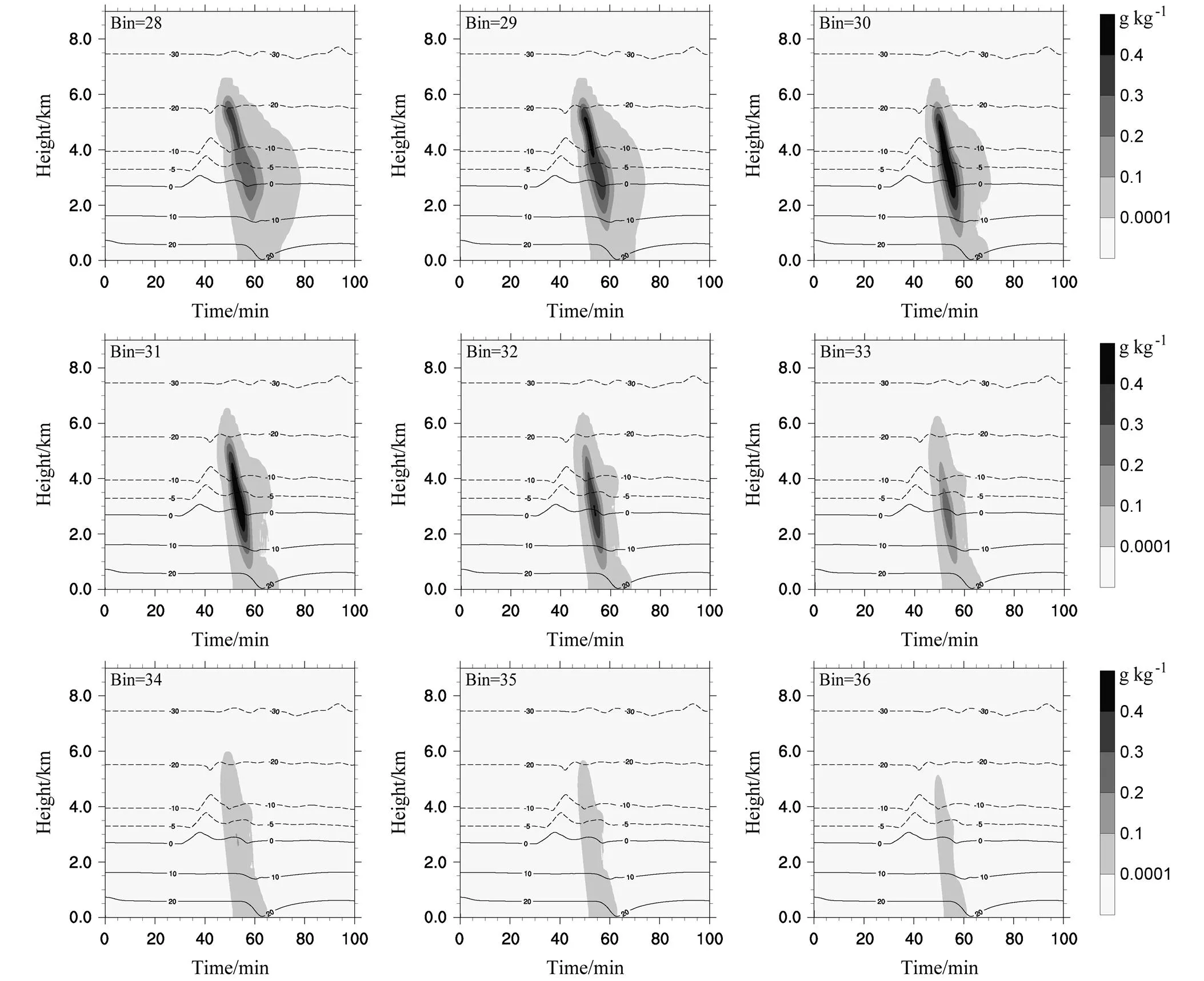
图20 （续）

4 结论

本文基于特拉维夫大学二维轴对称对流云全分档模式，将水成物粒子从34档增加到40档，修改了雪和霰的密度，加入了冻滴分档处理的微物理过程，发展和建立了一个包括液滴、冰晶、雪、霰和冻滴的全分档对流云模式。利用改进模式对一次强对流天气的理想过程进行数值模拟试验。研究冻滴过程加入后对云内物理量场和水成物粒子演变特征的影响，得到以下结论：

（1）改进的二维分档对流云模式中，冻滴主要由两个过程产生：半径大于80 μm的液滴冻结形成冻滴；霰与半径大于100 μm的液滴碰撞转化为冻滴。

（2）分析了模式改进后物理量场的特征：40 min时，温度升高、垂直上升速度及水面和冰面饱和度达到最大，有利于云内液相和固相粒子的形成增长，促进对流发展；60 min时，垂直下沉速度最大，温度降低，水面和冰面饱和度减小，对流减弱，促进降水产生。

（3）分析了模式改进后水成物粒子的分布特征：霰的生成机制受到抑制，浓度减小；冻滴产生，繁生产生的冰晶增多；冰晶聚并形成雪，雪的浓度增加；冻滴消耗过冷水增长，导致液态水浓度减小。

（4）分析了冻滴的动力场和微物理场的分布特征。冻滴形成前期，垂直上升速度和液态水含量增大且大值中心位置上移，液态水大值中心位于垂直上升速度大值中心上方，形成液态水累积区。液滴随着上升气流到达负温度区，冻结生成冻滴，霰与半径大于100 μm的液滴碰撞也生成冻滴。因此，44 min时，5 km的高度层有冻滴形成。冻滴在垂直上升气流的支撑下碰并过冷水增长，当上升气流托不住长大的冻滴，冻滴下落返回液态水累积区且继续增长，冻滴含量增大，液态水含量减小。

Alheit R R, Flossmann A I, Pruppacher H R. 1990. A theoretical study of the wet removal of atmospheric pollutants. Part IV: The uptake and redistribution of aerosol particles through nucleation and impaction scavenging by growing cloud drops and ice particles [J]. J. Atmos. Sci., 47 (7): 870–887, doi:10.1175/1520-0469(1990)047<0870:ATSOTW>2.0. CO;2.

Beard K V. 1977. Terminal velocity adjustment for cloud and precipitation [J]. J. Atmos. Sci., 34 (8): 1293–1298, doi:10.1175/1520-0469(1977) 034<1293:TVAFCA>2.0.CO;2.

Benmoshe N, Pinsky M, Pokrovsky A, et al. 2012. Turbulent effects on the microphysics and initiation of warm rain in deep convective clouds: 2-D simulations by a spectral mixed-phase microphysics cloud model [J]. J. Geophys. Res., 117(D6): D06220, doi:10.1029/2011JD016603.

Bigg E K. 1953. The formation of atmospheric ice crystals by the freezing of droplets [J]. Quart. J. Roy. Meteor. Soc., 79 (342): 510–519, doi:10. 1002/qj.49707934207.

Böhm H P. 1989. A general equation for the terminal fall speed of solid hydrometeors [J]. J. Atmos. Sci., 46 (15): 2419–2427, doi:10.1175/1520- 0469(1989)046<2419:AGEFTT>2.0.CO;2.

Bott A. 1998. A flux method for the numerical solution of the stochastic collection equation [J]. J. Atmos. Sci., 55 (13): 2284–2293, doi:10.1175/ 1520-0469(1998)055<2284:AFMFTN>2.0.CO;2.

Braham Jr R R. 1964. What is the role of ice in summer rain-showers? [J] J. Atmos. Sci., 21 (6): 640–645, doi:10.1175/1520-0469(1964)021<0640: WITROI>2.0.CO;2.

Chen J P. 1922. Numerical simulations on the redistribution of atmospheric trace chemicals through cloud processes [D]. Ph. D. dissertation, The Pennsylvania State University.

Cheng K Y, Wang P K, Wang C K. 2014. A numerical study on the ventilation coefficients of falling hailstones [J]. J. Atmos. Sci., 71 (7): 2625–2634, doi:10.1175/JAS-D-13-0229.1.

Cotton W R, Tripoli G J, Rauber R M, et al. 1986. Numerical simulation of the effects of varying ice crystal nucleation rates and aggregation processes on orographic snowfall [J]. J. Climate Appl. Meteor., 25 (11): 1658–1680, doi:10.1175/1520-0450(1986)025<1658:NSOTEO>2.0.CO; 2.

Farley R D, Orville H D. 1986. Numerical modeling of hailstorms and hailstone growth. Part I: Preliminary model verification and sensitivity tests [J]. J. Climate Appl. Meteor., 25 (12): 2014–2035, doi:10.1175/ 1520-0450(1986)025<2014:NMOHAH>2.0.CO;2.

Feingold G, Tzivion S, Leviv Z. 1988. Evolution of raindrop spectra. Part I: Solution to the stochastic collection/breakup equation using the method of moments [J]. J. Atmos. Sci., 45 (22): 3387–3399, doi:10.1175/1520- 0469(1988)045<3387:EORSPI>2.0.CO;2.

郭学良, 黄美元, 洪延超, 等. 2001a. 三维冰雹分档强对流云数值模式研究 I：模式建立及冰雹的循环增长机制[J]. 大气科学, 25 (5): 707–720. Guo Xueliang, Huang Meiyuan, Hong Yanchao, et al. 2001a. A study of three-dimensional hail-category hailstorm model. Part I: Model description and the mechanism of hail recirculation growth [J]. Chinese Journal of Atmospheric Sciences (in Chinese), 25 (5): 707–720, doi:10.3878/j.issn.1006-9895.2001.05.13.

郭学良, 黄美元, 洪延超, 等. 2001b. 三维冰雹分档强对流云数值模式研究 II：冰雹粒子的分布特征[J]. 大气科学, 25 (6): 856–864. Guo Xueliang, Huang Meiyuan, Hong Yanchao, et al. 2001b. A study of three-dimensional hail-category hailstorm model. Part II: Characteristics of hail-category size distribution [J]. Chinese Journal of Atmospheric Sciences (in Chinese), 25 (6): 856–864, doi:10.3878/j.issn.1006-9895. 2001.06.13.

Hall W D. 1980. A detailed microphysical model within a two-dimensional dynamic framework: Model description and preliminary results [J]. J. Atmos. Sci., 37 (11): 2486–2507, doi:10.1175/1520-0469(1980)037< 2486:ADMMWA>2.0.CO;2.

Hallett J, Mossop S C. 1974. Production of secondary ice crystals during the riming process [J]. Nature, 249: 26–28.

Hanesiak J M, Stewart R E. 1995. The mesoscale and microscale structure of a severe ice pellet storm [J]. Mon. Wea. Rev., 123 (11): 3144–3162, doi:10.1175/1520-0493(1995)123<3144:TMAMSO>2.0.CO;2.

Khain A P, Sednev I. 1996. Simulation of precipitation formation in the eastern Mediterranean coastal zone using a spectral microphysics cloud ensemble model [J]. Atmos. Res., 43 (1): 77–110, doi:10.1016/S0169- 8095(96)00005-1.

Khain A, Ovtchinnikov M, Pinsky M, et al. 2000. Notes on the state-of- the-art numerical modeling of cloud microphysics [J]. Atmos. Res., 55 (3–4): 159–224, doi:10.1016/S0169-8095(00)00064-8.

Khain A, Pokrovsky A, Pinsky M, et al. 2004. Simulation of effects of atmospheric aerosols on deep turbulent convective clouds using a spectral microphysics mixed-phase cumulus cloud model. Part I: Model description and possible applications [J]. J. Atmos. Sci., 61 (24): 2963–2982, doi:10.1175/JAS-3350.1.

Khvorostyanov V I, Khain A P, Kogteva E L. 1989. A two-dimensional non-stationary micro-physical model of a three phase convective cloud and evaluation of the effects of seeding by crystallizing reagent [J]. Sov. Meteor. Hydrol., 5: 33–45.

Kogan Y L. 1991. The simulation of a convective cloud in a 3-D model with explicit microphysics. Part I: Model description and sensitivity experiments [J]. J. Atmos. Sci., 48 (9): 1160–1189, doi:10.1175/1520- 0469(1991)048<1160:TSOACC>2.0.CO;2.

Kumjian M R, Ganson S M, Ryzhkov A V. 2012. Freezing of raindrops in deep convective updrafts: A microphysical and polarimetric model [J]. J. Atmos. Sci., 69 (12): 3471–3490, doi:10.1175/JAS-D-12-067.1.

Lew J K, Kingsmill D E, Montague D C. 1985. A theoretical study of the collision efficiency of small planar ice crystals colliding with large supercooled water drops [J]. J. Atmos. Sci., 42 (8): 857–862, doi:10.1175/ 1520-0469(1985)042<0857:ATSOTC>2.0.CO;2.

刘晓莉. 2007. 基于粒子分档技术的云模式研究 [D]. 南京信息工程大学博士学位论文. Liu Xiaoli. 2007. Researches on cloud model with spectral bin microphysics [D]. Ph. D. dissertation (in Chinese), Nanjing University of Information Science and Technology, doi:10.7666/d. y1079894.

刘晓莉, 牛生杰. 2007. 微物理过程分档处理的三维对流云模式研究 [J]. 南京气象学院学报, 30 (5): 617–622. Liu Xiaoli, Niu Shengjie. 2007. Development of 3-D convective cloud model based on spectral bin microphysics [J]. J. Nanjing Inst. Meteor. (in Chinese), 30 (5): 617–622, doi:10.3969/j.issn.1674-7097.2007.05.005.

刘晓莉, 牛生杰. 2009. 三维对流云中粒子谱演变特征的数值模拟 [J]. 中国科学 D辑: 地球科学, 39 (2): 245–256. Liu Xiaoli, Niu Shengjie. 2009. Numerical simulation on the evolution of cloud particles in 3-D convective cloud [J]. Sci. China Ser. D: Earth Sci., 52 (8): 1195–1206, doi:10.1007/s11430-009-0112-1.

Locatelli J D, Hobbs P V. 1974. Fall speeds and masses of solid precipitation particles [J]. J. Geophys. Res., 79 (15): 2185–2197, doi:10.1029/ JC079i015p02185.

Long A B. 1974. Solutions to the droplet collection equation for polynomial kernels [J]. J. Atmos. Sci., 31 (4): 1040–1052, doi:10.1175/1520-0469 (1974)031<1040:STTDCE>2.0.CO;2.

Low T B, List R. 1982a. Collision, coalescence and breakup of raindrops. Part I: Experimentally established coalescence efficiencies and fragment size distributions in breakup [J]. J. Atmos. Sci., 39 (7): 1591–1606, doi:10.1175/1520-0469(1982)039<1591:CCABOR>2.0.CO;2.

Low T B, List R. 1982b. Collision, coalescence and breakup of raindrops. Part II: Parameterization of fragment size distributions [J]. J. Atmos. Sci., 39 (7): 1607–1619, doi:10.1175/1520-0469(1982)039<1607:CCABOR> 2.0.CO;2.

Martin J J, Wang P K, Pruppacher H R, et al. 1981. A numerical study of the effect of electric charges on the efficiency with which planar ice crystals collect supercooled cloud drops [J]. J. Atmos. Sci., 38 (11): 2462–2469, doi:10.1175/1520-0469(1981)038<2462:ANSOTE>2.0.CO; 2.

Meyers M P, DeMott P J, Cotton W R. 1992. New primary ice-nucleation parameterizations in an explicit cloud model [J]. J. Appl. Meteor., 31 (7): 708–721, doi:10.1175/1520-0450(1992)031<0708:NPINPI>2.0.CO;2.

Morrison H, Grabowski W W. 2010. An improved representation of rimed snow and conversion to graupel in a multicomponent bin microphysics scheme [J]. J. Atmos. Sci., 67 (5): 1337–1360, doi:10.1175/ 2010JAS3250.1.

Mossop S C. 1978. The influence of drop size distribution on the production of secondary ice particles during graupel growth [J]. Quart. J. Roy. Meteor. Soc., 104 (440): 323–330.

Ochs III H T, Czys R R, Beard K V. 1986. Laboratory measurements of coalescence efficiencies for small precipitation drops [J]. J. Atmos. Sci., 43 (3): 225–232, doi:10.1175/1520-0469(1986)043<0225:LMOCEF>2.0. CO;2.

Orville H D, Kopp F J. 1977. Numerical simulation of the life history of a hailstorm [J]. J. Atmos. Sci., 34 (10): 1596–1618, doi:10.1175/1520- 0469(1977)034<1596:NSOTLH>2.0.CO;2.

Phillips V T J, Khain A, Benmoshe N, et al. 2015. Theory of time-dependent freezing. Part II: scheme for freezing raindrops and simulations by a cloud model with spectral bin microphysics [J]. J. Atmos. Sci., 72 (1): 262–286, doi:10.1175/JAS-D-13-0376.1.

Pruppacher H R, Klett J D. 1997. Microphysics of Clouds and Precipitation [M]. Boston: Kluwer Academic Publishers, 707pp.

Rasmussen R M, Heymsfield A J. 1985. A generalized form for impact velocities used to determine graupel accretional densities [J]. J. Atmos. Sci., 42 (21): 2275–2279, doi:10.1175/1520-0469(1985)042<2275: AGFFIV>2.0.CO;2.

Rasmussen R M, Heymsfield A J. 1987. Melting and shedding of graupel and hail. Part I: Model physics [J]. J. Atmos. Sci., 44 (19): 2254–2263, doi:10.1175/1520-0469(1987)044<2754:MASOGA>2.0.CO;2.

Reisin T, Levin Z, Tzivion S. 1996. Rain production in convective clouds as simulated in an axisymmetric model with detailed microphysics. Part II: Effects of varying drops and ice initiation [J]. J. Atmos. Sci., 53 (13): 1815–1837, doi:10.1175/1520-0469(1996)053<1815:RPICCA>2.0.CO;2.

Ryzhkov A V, Kumjian M R, Ganson S M, et al. 2013. Polarimetric radar characteristics of melting hail. Part I: theoretical simulations using spectral microphysical modeling [J]. J. Appl. Meteor. Climatol., 52 (12): 2849–2870, doi:10.1175/JAMC-D-13-073.1.

Sato Y, Nakajima T Y, Nakajima T. 2012. Investigation of the vertical structure of warm-cloud microphysical properties using the cloud evolution diagram, CFODD, simulated by a three-dimensional spectral bin microphysical model [J]. J. Atmos. Sci., 69 (6): 2012–2030, doi:10.1175/JAS-D-11-0244.1.

盛裴轩, 毛节泰, 李建国, 等. 2003. 大气物理学 [M]. 北京: 北京大学出版社，522pp. Sheng Peixuan, Mao Jietai, Li Jianguo, et al. 2003. Atmospheric Physics (in Chinese) [M]. Beijing: PekingUniversityPress, 522pp.

Smolarkiewicz P K. 1983. A simple positive definite advection scheme with small implicit diffusion [J]. Mon. Wea. Rev., 111 (3): 479–486, doi:10.1175/1520-0493(1983)111<0479:ASPDAS>2.0.CO;2.

Soong S T, Tao W K. 1980. Response of deep tropical cumulus clouds to mesoscale processes [J]. J. Atmos. Sci., 37 (9): 2016–2034, doi:10.1175/ 1520-0469(1980)037<2016:RODTCC>2.0.CO;2.

Soong S T, Ogura Y. 1980. Response of tradewind cumuli to large-scale processes [J]. J. Atmos. Sci., 37 (9): 2035–2050, doi:10.1175/1520- 0469(1980)037<2035:ROTCTL>2.0.CO;2.

Sun J M, Ariya P A, Leighton H G, et al. 2010. Mystery of ice multiplication in warm-based precipitating shallow cumulus clouds [J]. Geophys. Res. Lett., 37 (10): L10802, doi:10.1029/2010GL042440.

Sun J M, Ariya P A, Leighton H G, et al. 2012a. Modeling study of ice formation in warm-based precipitating shallow cumulus clouds [J]. J. Atmos. Sci., 69 (11): 3315–3335, doi:10.1175/JAS-D-11-0344.1.

Sun J M, Leighton H, Yau M K, et al. 2012b. Numerical evidence for cloud droplet nucleation at the cloud-environment interface [J]. Atmos. Chem. Phys., 12 (7): 17723–17742, doi:10.5194/acp-12-12155-2012.

Takahashi T. 1976. Hail in an axisymmetric cloud model [J]. J. Atmos. Sci., 33 (8): 1579–1601, doi:10.1175/1520-0469(1976)033<1579:HIAACM> 2.0.CO;2.

Tao W K, Simpson J. 1993. Goddard cumulus ensemble model. Part I: Model description [J]. Terr. Atmos. Oceanic Sci., 4 (1): 35–72.

Tao W K, Simpson J, Baker D, et al. 2003. Microphysics, radiation and surface processes in the Goddard Cumulus Ensemble (GCE) model [J]. Meteor. Atmos. Phys., 82 (1–4): 97–137, doi:10.1007/s00703-001-0594-7.

Tzivion S, Feingold G, Levin Z. 1987. An efficient numerical solution to the stochastic collection equation [J]. J. Atmos. Sci., 44 (21): 3139–3149, doi:10.1175/1520-0469(1987)044<3139:AENSTT>2.0.CO;2.

Tzivion S, Feingold G, Levin Z. 1989. The evolution of raindrop spectra. Part II: Collisional collection/breakup and evaporation in a rainshaft [J]. J. Atmos. Sci., 46 (21): 3312–3328, doi:10.1175/1520-0469(1989)046< 3312:TEORSP>2.0.CO;2.

Wang C, Chang J S. 1993. A three-dimensional numerical model of cloud dynamics, microphysics, and chemistry. I: Concepts and formulation [J]. J. Geophys. Res., 98 (D8): 14827–14844, doi:10.1029/92JD01393.

肖辉, 徐华英, 黄美元. 1988a. 积云中云滴谱形成的数值模拟研究（一）——盐核谱和浓度的作用[J]. 大气科学, 12 (2): 121–130. Xiao Hui, Xu Huaying, Huang Meiyuan. 1988a. A study of numerical simulation on the formation of the cloud droplet spectra in cumulus clouds—Part I: The roles of spectra and concentration of salt nuclei [J]. Chinese Journal of Atmospheric Sciences (Scientia Atmos. Sinica) (in Chinese), 12 (2): 121–130,doi:10.3878/j.issn.1006-9895.1988.02.02.

肖辉, 徐华英, 黄美元. 1988b. 积云中云滴谱形成的数值模拟研究（二）——各种碰并过程、大气层结等的作用[J]. 大气科学, 12 (3): 312– 319. Xiao Hui, Xu Huaying, Huang Meiyuan. 1988b. A study of numerical simulation on the formation of the cloud droplet spectra in cumulus clouds—Part II: The roles of various collision processes, atmospheric stratifications and miscellaneous [J]. Chinese Journal of Atmospheric Sciences (Scientia Atmos. Sinica) (in Chinese), 12 (3): 312–319, doi:10.3878/j.issn.1006-9895.1988.03.11.

许焕斌. 1995. 云系模式研究：云场的宏微观结构模拟 [J]. 气象学报, 53 (3): 349–357. Xu Huanbin. 1995. A study of cloud-system model: Macro and micro structure simulation of cloud field [J]. Acta Meteor. Sinica (in Chinese), 53 (3): 349–357,doi:10.11676/qxxb1995.040.

许焕斌. 2012. 强对流云物理及其应用 [M]. 北京: 气象出版社，340pp. Xu Huanbin. 2012. The Physics of Severe Convective Storms and Its Application (in Chinese) [M]. Beijing: China Meteorological Press, 340pp.

许焕斌, 段英. 1999. 云粒子谱演化研究中的一些问题 [J]. 气象学报, 57 (4): 450–460. Xu Huanbin, Duan Ying. 1999. Some questions in studying the evolution of size-distribution spectrum of hydrometeor particles [J]. Acta Meteor. Sinica (in Chinese), 57 (4): 450–460, doi:10.11676/qxxb1999.042.

徐华英, 黄培强, 黄美元, 等. 1983. 积云中云滴群凝结增长的数值模拟[J]. 大气科学, 7 (3): 249–259. Xu Huaying, Huang Peiqiang, Huang Meiyuan, et al. 1983. A study on the growth of cloud droplets by condensation in cumulus clouds [J]. Chinese Journal of Atmospheric Sciences(Scientia Atmos. Sinica) (in Chinese), 7 (3): 249–259, doi:10.3878/j.issn.1006-9895.1983.03.02.

Yin Y, Levin Z, Reisin T G, et al. 2000a. The effects of giant cloud condensation nuclei on the development of precipitation in convective clouds—A numerical study [J]. Atmos. Res., 53 (1–3): 91–116, doi:10.1016/S0169-8095(99)00046-0.

Yin Y, Levin Z, Reisin T G, et al. 2000b. Seeding convective clouds with hygroscopic flares: Numerical simulations using a cloud model with detailed microphysics [J]. J. Appl. Meteor., 39 (9): 1460–1472, doi:10.1175/1520-0450(2000)039<1460:SCCWHF>2.0.CO;2.

Yin Y, Carslaw K S, Parker D J. 2002a. Redistribution of trace gases by convective clouds-mixed-phase processes [J]. Atmos. Chem. Phys., 2 (4): 293–306, doi:10.5194/acp-2-293-2002.

Yin Y, Wurzler S, Levin Z, et al. 2002b. Interactions of mineral dust particles and clouds: Effects on precipitation and cloud optical properties [J]. J. Geophys. Res., 107 (D23): AAC 19-1–AAC 19-14, doi:10.1029/2001JD001544 .

Yin Y, Carslaw K S, Feingold G. 2005. Vertical transport and processing of aerosols in a mixed-phase convective cloud and the feedback on cloud development [J]. Quart. J. Roy. Meteor. Soc., 131 (605): 221–245, doi:10.1256/qj.03.186.

赵仕雄, 许焕斌, 德力格尔. 2004. 黄河上游对流云降水微物理特征的数值模拟试验[J]. 高原气象, 23 (4): 495–500. Zhao Shixiong, Xu Huanbin, Deli Geer. 2004. Numerical simulation of microphysical character of convective cloud precipitation in upper reach of Yellow River [J]. Plateau Meteor. (in Chinese), 23 (4): 495–500, doi:10.3321/j. issn:1000-0534.2004.04.012.

徐戈, 孙继明, 牛生杰, 等. 2016. 冻滴微物理过程的分档数值模拟试验研究[J]. 大气科学, 40 (6): 1297–1319. Xu Ge, Sun Jiming, Niu Shengjie, et al. 2016.A numerical study for the microphysical processes of ice pellets with a spectral (bin) cloud model [J]. Chinese Journal of Atmospheric Sciences (in Chinese), 40 (6): 1297–1319, doi:10.3878/j.issn.1006-9895.1601.15156.

A Numerical Study for the Microphysical Processes of Ice Pellets with a Spectral (bin) Cloud Model

XU Ge1, 2, SUN Jiming2, 1, NIU Sheng jie1, ZHOU Bi3, and WANG Yongqing2

1,,210044;2,,,100029;3,, Changsha 410118

Graupel and frozen drops are the main source of deep convective precipitation. The terminal falling velocity of graupel and frozen drops are different because of the difference between their densities. As a result, cloud microphysical processes and the temporal and spatial distribution of precipitation will change. Based on the two-dimensional axisymmetric convective cloud model developed by Tel Aviv University in Israel with detailed treatments of both the warm and cold microphysical processes, the authors increased the bins of hydrometeors from 34 to 40 and modified the graupel and snow densities and developed a bin microphysical model that includes water drops, ice crystals, snow, graupel, and ice pellets. The authors used the improved model to simulate an ideal case of severe convective cloud and analyzed the characteristics of the dynamical fields and hydrometeor distributions. Results of the present study were compared with simulations by the original model.The results showed that: (1) Ice pellets can produce a large amount of ice crystals due to their high terminal velocities, which results in the falling of ice pellets into the ice multiplication zone that is determined by the temperature and concentration of cloud droplets;(2) there is a liquid water accumulation zone before the ice pellet formation, because the maximum area of liquid water is located above the maximum vertical velocity zone. At the stage of ice pellet formation, the liquid water accumulation zone is above the level of 0°C. The ice pellets are formed by water drop freezing and graupel riming with the water drop radius greater than 100 μm. At the stage of ice pellet growth, the ice pellets grow due to the accretion of supercooled water, leading to ice pellet water content increase and liquid water content decrease. The modeling results showed that the improved model could successfully simulate the ice pellet formation process. The improved spectral microphysical scheme will be coupled into the WRF (Weather Research and Forecasting model) to study the formation mechanism of hails under more complicated dynamical conditions.

Convective cloud, Ice pellet, Spectral (bin) microphysical model

1006-9895(2016)06-1297-23

P401

A

10.3878/j.issn.1006-9895.1601.15156

2015-03-16；网络预出版日期 2016-01-27

徐戈，女，1988年出生，硕士研究生，主要从事云和降水物理学研究。E-mail: xugejy@163.com

孙继明，E-mail: jimings@mail.iap.ac.com

国家重点基础研究发展计划（973计划）项目2014CB441403，中国科学院百人计划项目Y16B015601，国家自然科学基金项目41375138，江苏高校优势学科建设工程项目（PAPD）

National Basic Research Program of China (973 Program, Grant 2014CB441403),One Hundred Talents Project of the Chinese Academy of Sciences (Grant Y16B015601), National Natural Science Foundation of China (Grant 41375138), Priority Academic Program Development of Jiangsu Higher Education Institutions