翼面结冰过程中的冰晶运动相变与黏附特性
马乙楗,柴得林,王强,易贤,*,孔满昭
1.中国空气动力研究与发展中心 结冰与防除冰重点实验室,绵阳 621000
2.中国空气动力研究与发展中心 空气动力学国家重点实验室,绵阳 621000
3.航空工业第一飞机设计研究院,西安 710089
航空发动机摄入冰晶易发生结冰,进而导致发动机动力损失或损坏[1-2]。相比于传统过冷水结冰,冰晶结冰存在冰晶运动、相变、黏附等物理现象,结冰机理复杂[3-5]。由于研究冰晶结冰的实验设备复杂、成本昂贵[6],有必要开展冰晶结冰数值计算方法研究[7]。在冰晶结冰计算中,冰晶的运动相变决定了撞击壁面的冰晶的形态与撞击位置,黏附特性决定了参与结冰相变的冰晶的质量通量,二者直接关系到壁面冰形的增长与发展,是准确模拟冰晶结冰现象的关键环节[8]。因此,为深刻认识冰晶结冰现象,需要开展冰晶运动相变与黏附计算方法研究,系统分析冰晶运动相变与黏附特性。
围绕冰晶运动相变以及冰晶黏附过程,国内外研究者开展了一系列研究,研究表明冰晶形状对冰晶运动以及相变过程有显著影响[9-11],Norde等[12]模拟了冰晶运动过程中的传热过程,指出粒子运动和传热强烈依赖于冰晶形状,在冰晶大量融化之前冰晶形状通常为非球状;Nilamdeen和Habashz[13]假设冰晶为平板状,开展了冰晶的动力学特性研究,指出冰晶在流场的流动特性接近于圆盘状颗粒;Iuliano等[14]假设冰晶为圆柱或圆盘状,开展了冰晶阻力模型和传热过程的数值模拟;Trontin等[10]提出了冰晶的传热传质模型,并对自由流中的非球状冰晶颗粒传热传质进行了研究,通过实验所得冰形完善了冰晶黏附模型。郭向东等[11]假设冰晶为六角板状和六棱柱状,采用Villedieu等[15]提出的热力学模型研究了冰晶形状对其运动过程中换热和轨迹的影响。针对冰晶黏附效率,Zhang等[16]通过比较冰晶粒径和结构表面水膜厚度来判断冰晶是否黏附或破碎,该过程在Fluent软件上进行,计算得到黏附冰晶质量通量,进而计算出结冰冰形。Villedieu等[15]提出了基于结构表面水膜厚度、粒子表面水膜厚度、粒子等效粒径和法向动能恢复系数的冰晶黏附效率计算方法,该方法计算冰形与Trontin等[10]实验结果的吻合效果并不理想。Trontin等[10]提出了一种基于冰晶粒子融化率、总液态水含量和总水含量的冰晶黏附效率的计算方法,并根据NASA-NRC混合气象条件结冰的实验冰形数据校核了该黏附效率计算模型。综上,国内外学者已经围绕冰晶运动相变过程以及冰晶黏附过程建立了一系列数值计算模型,但在相关研究中,仅根据少数结冰实验、冰形数据确定了模型系数并做了简单模型验证,未开展冰晶形状对冰晶运动相变特性影响的深入研究,也未开展来流参数和冰晶融化效应对冰晶黏附特性影响的系统性分析与研究。
因此,本文建立了拉格朗日框架下冰晶运动-传热传质耦合的数值计算方法,分析基于Monte Carlo方法的冰晶撞击与黏附收集系数计算方法;依托NNWICE平台[17]开发相应的计算程序,实现冰晶运动-传热传质耦合与冰晶黏附的数值计算。以NACA0012翼型为对象,完成翼面冰晶/混合相结冰过程中,冰晶运动相变与黏附过程的模拟,研究冰晶形状对冰晶运动相变特性的影响,系统分析不同来流温度和液态水含量条件下冰晶的黏附特性,研究冰晶运动相变与黏附特性的影响规律。
1 计算方法
由于撞击到翼型表面的冰晶不一定全部黏附,黏附冰晶量需在撞击收集系数基础上进一步计算冰晶黏附特性得到。基于上述分析,计算冰晶黏附特性的流程如图1所示。首先,求解空气流场,为冰晶运动相变、水滴运动计算提供背景流场;再通过冰晶运动-传热传质计算得到冰晶撞击特性与撞击表面冰晶物态;最后,根据计算出的冰晶、水滴撞击特性和冰晶物态完成冰晶黏附特性计算。采用NNW-FlowStar软件完成空气流场计算,空间离散采用一阶迎风格式,通量格式采用Roe格式,湍流模型采用SST(Shear Stress Transport)k-ω模型。

图1 冰晶黏附特性计算流程Fig. 1 Calculation process of ice crystal adhesion characteristics
1.1 冰晶运动-相变计算
1) 冰晶运动控制方程
根据Stokes定理、牛顿第二定律,在拉格朗日框架下的冰晶运动控制方程为
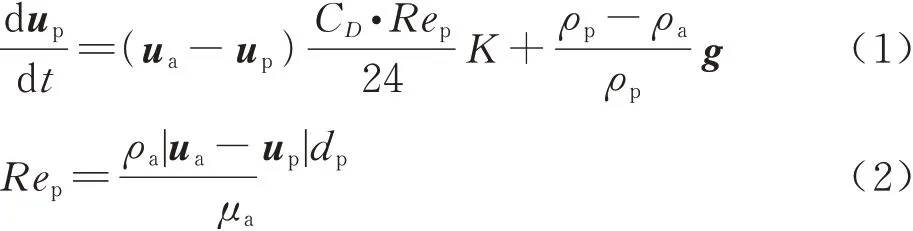
式中:up为冰晶运动速度;ua为空气速度;CD为阻力系数;Rep为冰晶相对雷诺数;μa为空气动力黏度;t为时间;ρa和ρp分别为空气和冰晶粒子的密度;g为重力加速度;dp为冰晶等效体积直径;系数
2) 冰晶形状参数与阻力系数
采用以下形状参数表征不同形状冰晶[16]。
冰晶等效体积直径(dp)表示具有和冰晶粒子相同体积的球状冰晶的直径,即

式中:Vp为冰晶粒子的体积。
冰晶球度(Φ)表示等效球状冰晶表面积(Ap)与冰晶实际表面积(A)之比,即

冰晶横向球度(Φ⊥)表示等效球状冰晶的横截面积(Ap,⊥)与冰晶流向投影的横截面积(A⊥)之比,即

冰晶颗粒纵横比E(Aspect Ratio)表示冰晶轴向长度b(沿旋转轴)与径向长度a(垂直于旋转轴)之比,即

通常冰晶形状以板状和柱状为主[11]。为模拟对流云内的冰晶颗粒,表1给出了球状和3种非球状冰晶粒子的相关形状参数计算公式[15]。
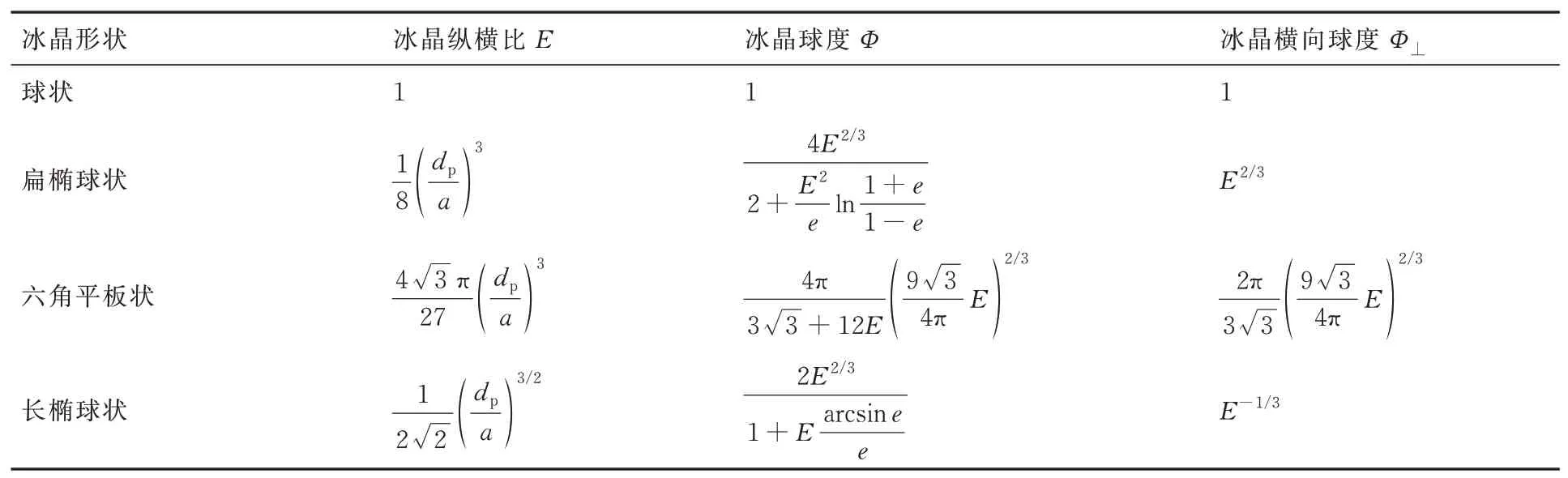
表1 冰晶形状参数计算公式[15]Table 1 Calculation formulas for ice crystal shape parameters[15]
Hölzer和Sommerfeld[18]提出了一种考虑粒子方向并适用于所有形状粒子的阻力系数表达式,本文采用式(7)计算式(1)中的冰晶阻力系数。
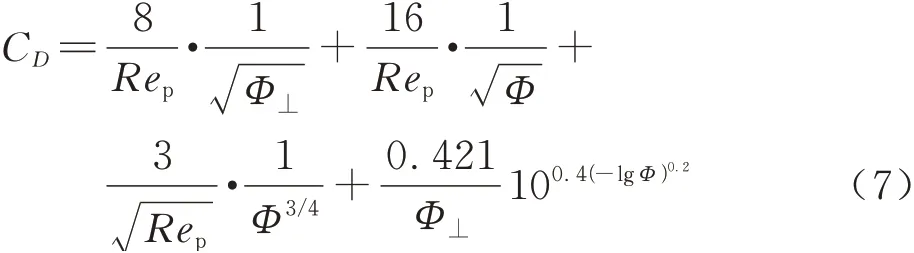
3) 冰晶相变模型
根据Trontin等[10]提出的相变模型,冰晶运动中的相变过程分为3个阶段:① 过冷冰晶阶段,冰晶温度低于融化温度,吸热后温度逐渐升高,仅发生升华;② 冰晶融化阶段,冰晶温度保持为融化温度,吸热后发生融化与蒸发,直至完全融化;③ 水滴蒸发阶段,冰晶完全融化为水滴,温度高于融化温度,吸热后温度不断升高,仅发生蒸发。
图2展示了各阶段冰晶状态,其中Tp表示冰晶粒子温度,Tm表示冰晶融化温度。各阶段传热传质计算公式见文献[10]。
4) 冰晶运动相变计算方法
冰晶运动方程与传热传质方程采用一阶欧拉向前时间离散格式进行求解,对于冰晶运动控制方程式(1),其离散形式为
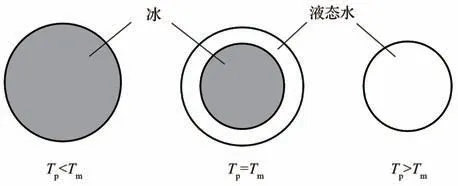
图2 各阶段冰晶状态示意图Fig. 2 Schematic diagram of state of ice crystals at each stage
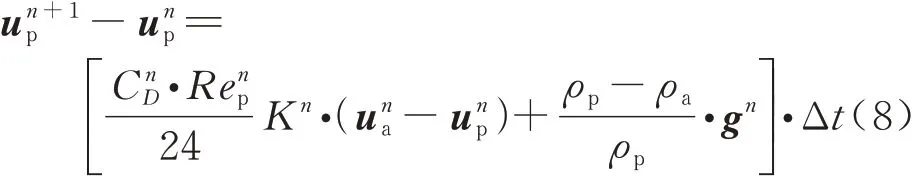
式中:n代表第n个时间步;Δt代表时间步长。而冰晶传热传质方程根据冰晶所处状态不同,具体公式见文献[10]。
通常冰晶运动伴随传热传质发生,本文按以下计算方法求解冰晶运动-相变耦合模型:① 初始化冰晶参数(冰晶初始位置、粒径、形状、初始温度);② 采用径向基函数插值方法由冰晶空气流场变量插值得到冰晶所在位置处物理量;③ 求解冰晶相变方程更新冰晶质量、形态、球度、温度等参数与变量;④ 将与求解运动方程相关的参数变量代入运动方程,计算更新冰晶位置、速度等变量;⑤ 重复步骤2~步骤4直至冰晶撞击壁面/飞出指定区域或完全蒸发,完成轨迹求解。
1.2 冰晶黏附特性与收集系数计算
1) 冰晶撞击收集系数计算
采用基于统计原理的Monte Carlo方法[19-20]计算冰晶撞击收集系数,该方法既能适应复杂三维外形,又能克服轨迹交叉、冰晶运动过程中质量损失等问题。
在Monte Carlo方法下,冰晶撞击收集系数(βs,MC)的计算式为
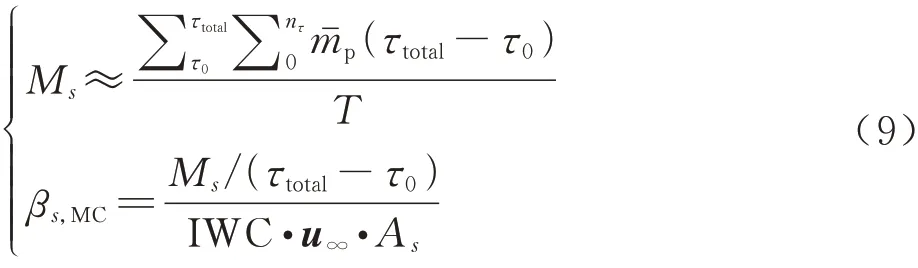
式 中:Ms为 网 格 单 元s从τ0到τtotal时 刻 的 质 量 流率积分;nτ为τ时刻撞击到s上的冰晶数量;mˉp为单个粒子的质量;T为总时间步数;As为表面单元s的面积;u∞表示来流速度;IWC表示来流冰水含量。
2) 冰晶融化率与黏附效应模型
定义mp,i为冰核质量即冰晶中冰的质量,则融化率ηm可定义为

式中:m表示冰晶总质量。
文献[21]提出了将黏附效率系数εs作为冰晶黏附效应的数学描述,其定义为黏附的冰晶质量与撞击冰晶质量之比,并给出了计算冰晶黏附效率的一种计算方式。首先定义当空气中只有冰晶以及融化冰晶时的黏附效率系数εs,c,其计算式为
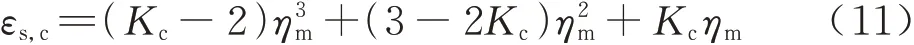
式中:Kc为比例常数,通常取Kc=2.5。
定义空气中同时含有冰晶和水滴时的黏附效率系数εs,d,计算式为

式中:Kd为比例常数,其计算式为
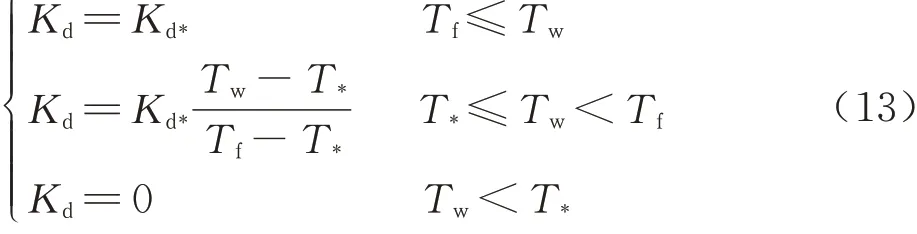
式中:Kd*=0.6;Tw为壁面处温度;Tf为冰晶融化温度,根据水的三相图可知在来流入口压力为98 000 Pa时,Tf=273.152 75 K;T*为冰晶完全无法黏附的阈值温度,取文献[21]中的建议值273.15 K。
φc表示撞击冰晶的质量分数,φd表示撞击水滴的质量分数,其计算式为
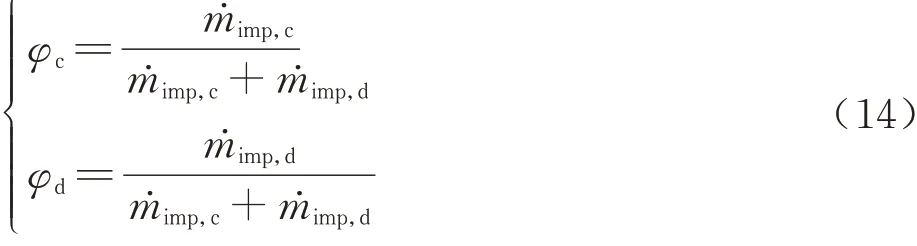
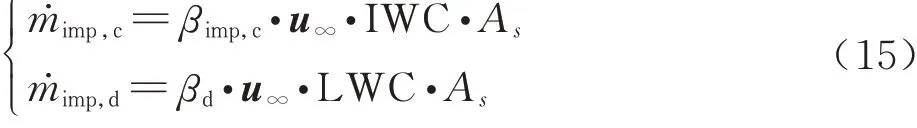
式中:βimp,c、βd分别表示冰晶、水滴撞击局部收集系数; LWC表示来流液态水含量。
对式(12)~式(15)进行推导,可得
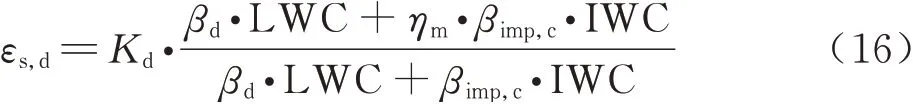
根据εs,c和εs,d,给出冰晶黏附效率εs和冰晶黏附收集系数βcatch的计算公式为

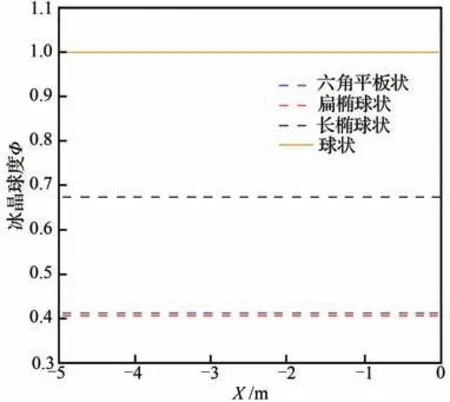
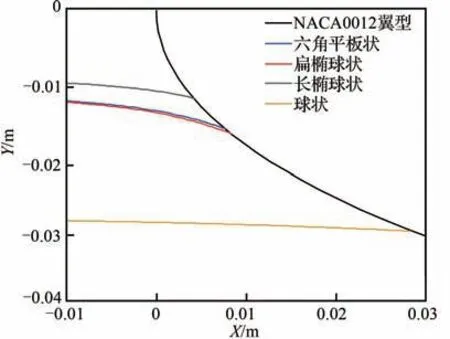
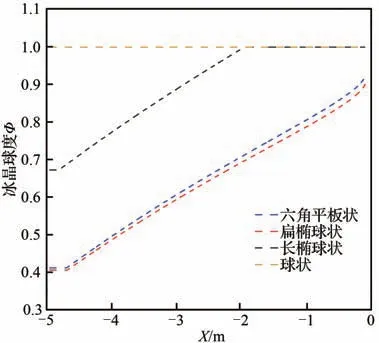
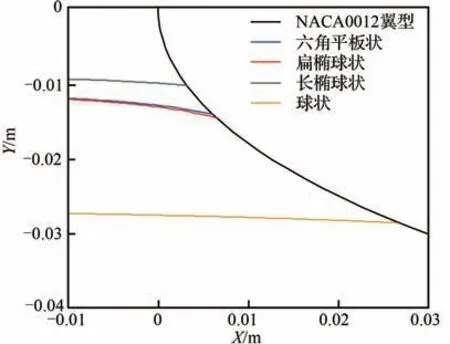
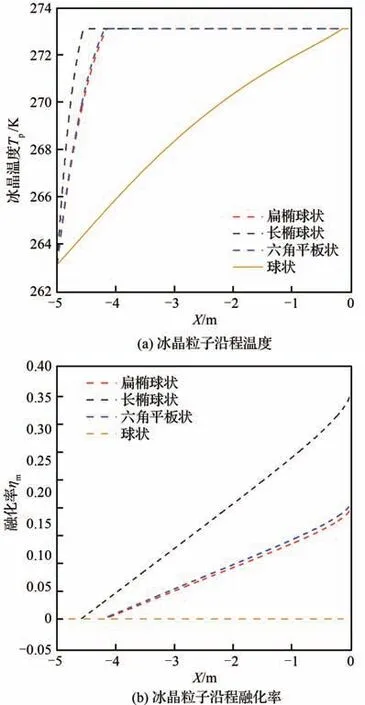
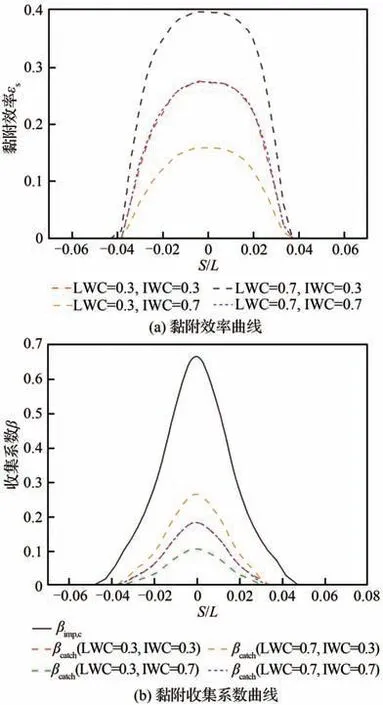
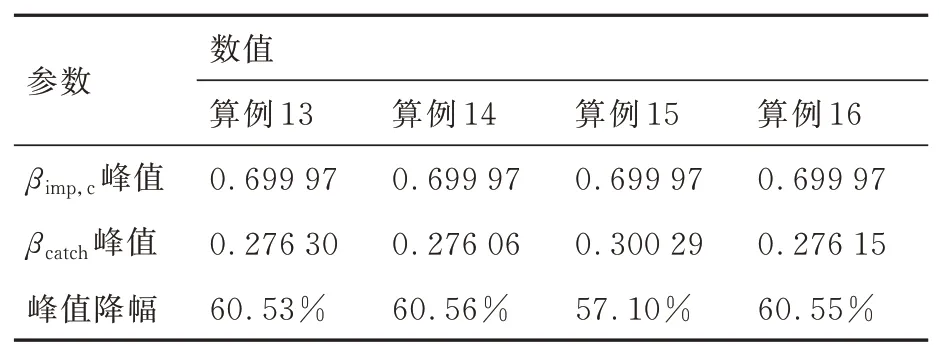
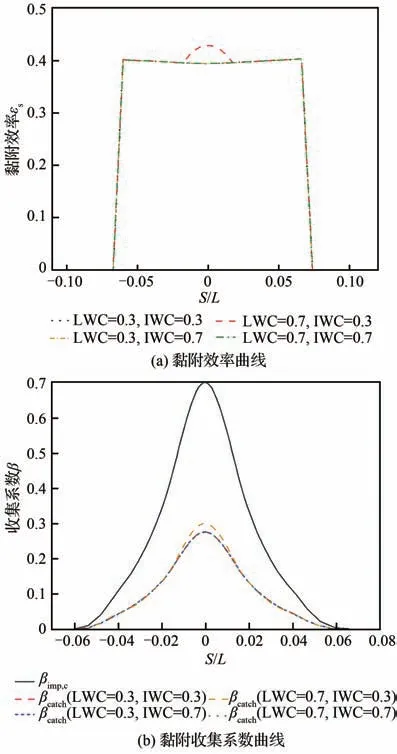
此外,式(13)表明壁面温度也会对冰晶黏附率产生影响。为探究融化率与来流液态水含量对冰晶黏附收集系数的影响,本文假设翼面温度为恒定值Tw=273.5 K,收集过程均在Tf 通过球度对冰晶形状特征进行数学描述,本节将讨论不同来流条件下,冰晶球度对冰晶运动轨迹的影响。 以二维NACA0012翼型作为结冰对象,翼型弦长为1 m,参照文献[13],按照表2设置来流参数并开展计算与分析,表中MVD表示冰晶粒子的平均容积直径。相同最大尺度(轴向长度与径向长度的较大者)的不同形状冰晶在运动过程中的沿程球度与运动轨迹结果如图3~图6所示。 当来流总温为−5 ℃时,由图3可看出,冰晶球度在运动过程中保持恒定。这是由于冰晶未发生融化。图4展示了同一位置释放的4种形状冰晶的运动轨迹,3种非球状冰晶运动轨迹较为接近且与球状差距较大。这是由于球状冰晶的质量与球度都明显大于非球状冰晶。图5给出了来流总温35 ℃冰晶沿程球度的变化。由图5可知,非球状冰晶融化前球度不变,开始融化后球度沿程增大,长椭球状冰晶球度将逐渐增大至1(融化为水滴);六角平板状以及扁椭球状冰晶球度接近且变化趋势基本一致。图6展示了来流总温35 ℃下同一位置释放4种冰晶的运动轨迹,与图4相似,非球状冰晶的运动轨迹接近且与球状冰晶的差距明显。算例1、算例2的数值实验结果证明,冰晶形状将对冰晶运动轨迹产生显著影响。 表2 工况参数Table 2 Running parameters 图3 来流总温−5 ℃下冰晶沿程球度Fig. 3 Sphericity of ice crystals along trajectory at total temperature of −5 ℃ 图4 来流总温−5 ℃下冰晶运动轨迹Fig. 4 Trajectories of ice crystals at total temperature of − 5 ℃ 图5 来流总温35 ℃下冰晶沿程球度Fig. 5 Sphericity of ice crystals along trajectory at total temperature of 35 ℃ 图6 来流总温35 ℃下冰晶运动轨迹Fig. 6 Trajectories of ice crystals at total temperature of 35 ℃ 采用表2所示的工况参数,仅改变来流总温为15 ℃、35 ℃设置算例3和算例4。计算得到相同最大尺度的不同形状冰晶的沿程温度及融化率变化曲线如图7、图8所示。 图7 来流总温15 ℃下冰晶粒子温度及融化率变化曲线Fig. 7 Variation of particle temperature and melting ratio at total temperature of 15 ℃ 图8 来流总温35 ℃下冰晶粒子温度及融化率变化曲线Fig. 8 Variation of particle temperature and melting ratio at total temperature of 35 ℃ 图7中不同形状的冰晶运动过程中温度与融化率变化曲线差异明显,长椭球状冰晶温升与融化最快,其次是扁椭球状和六角平板状冰晶,球状最慢;所有冰晶撞击到壁面时均未完全融化,而球状冰晶刚开始融化。这是由于球状冰晶的质量明显大于其余冰晶,升温所需外界能量更多。由于扁椭球状与六角平板状冰晶形状和球度类似,故其温升与融化速率差异较小。 图8给出了来流总温35 ℃时4种冰晶粒子温度及冰晶融化率变化曲线,冰晶温度与融化率变化趋势与算例3基本相同。由于来流总温更高,冰晶粒子换热更剧烈,升温与融化速率显著增加;相同冰晶撞击到壁面时,算例4中融化率较算例3增大;长椭球状冰晶已完全融化。 算例3和算例4的数值实验结果证明,冰晶形状对运动过程中冰晶温度与融化率具有显著影响,这将影响冰晶黏附特性及后续冰晶结冰相变过程中撞击到结构表面的冰晶粒子的显热、物态进而影响冰形计算;此外,在最大尺度相同的条件下,相较于扁椭球状和六角平板状冰晶,长椭球状冰晶在运动过程中换热、融化现象更显著。 云雾场通常是指包含由液态水滴和固态冰晶形成的云雾的空间区域,云雾场性能主要由以下云雾参数衡量:粒子的平均容积直径(MVD)、液态水含量(LWC)、冰水含量(IWC)、总水含量(TWC)等,上述参数是影响翼面结冰的重要因素。根据Currie等[22]的实验结果,冰晶黏附效率取决于撞击粒子的液态水含量与总水含量的比值。通常LWC来自于2部分:冰晶融化与混合相来流中的过冷水滴。为分析冰晶融化以及过冷水滴含量对冰晶收集系数的影响,将通过改变来流温度以及云雾参数开展数值计算研究。 采用150 μm六角平板状冰晶,参照表2设置其余工况参数,并改变来流总温分别为−5、5、15、35 ℃,对算例5~算例8进行数值实验。 图9给出了不同温度条件下的冰晶撞击收集系数和冰晶黏附效率(εs)。图中S表示翼型上下翼面的点到翼型前缘驻点的距离,L表示特征长度,此处为翼型的弦长。从图9(a)可看出来流总温为−5 ℃和5 ℃下的冰晶撞击收集系数(βimp,c)曲线接近,随着来流总温升高冰晶的撞击极限和撞击收集系数峰值均增大。−5 ℃与5 ℃的冰晶均未进入融化阶段,质量损失均很小,撞击收集系数曲线相似。随着来流总温升高至冰晶融化,冰晶在靠近翼型表面绕流时随流性变弱,冰晶撞击收集系数峰值、撞击极限增大。 图9 冰晶撞击收集系数与黏附效率曲线Fig. 9 Ice crystal impingement coefficient and sticking efficiency 由图9(b)可知算例5与算例6的黏附效率曲线接近且呈钟形。算例7与算例8冰晶黏附效率的范围以及峰值较算例5与算例6显著增大且维持在某一定值附近。对于算例5与算例6,由于冰晶并未融化,黏附效率完全取决于水滴收集量,曲线呈钟形。随着来流总温的升高冰晶开始融化,这时黏附效率大小主要取决于融化率(ηm)和水滴收集系数(βd),其值取水滴对应黏附效率(εs,d)与 冰 晶 融 化 对 应 黏 附 效 率(εs,c)中 较 大 值。故算例7与算例8中冰晶黏附效率范围与冰晶撞击收集系数范围一致。此外,算例7中靠近前缘附近水滴导致的黏附效应相较于冰晶融化导致的黏附效应更明显,该区域的黏附效率明显增高。 图10给出了−5 ℃、15 ℃和35 ℃下冰晶、水滴收集系数和冰晶黏附收集系数(βcatch)曲线,图10(d)给出了3种来流总温条件下冰晶黏附收集系数曲线。选取收集系数曲线主要特征量——收集系数峰值和撞击上极限弧面坐标值,并进行对比,表3给出了相应的数据,表中Tt∞为来流总温,峰值降幅指βcatch,峰值相对于βimp,c峰值的降幅,上极限降幅指黏附上极限弧面坐标相对于撞击上极限弧面坐标的降幅。 图10 混合相条件下冰晶和水滴收集系数曲线Fig. 10 Ice crystal and droplet collection coefficient under mixed phase conditions 表3 不同来流总温收集系数曲线主要特征对比Table 3 Comparison of main characteristics of collection coefficient at different total temperatures 如图10(a)所示,在来流总温−5 ℃下冰晶不融化,冰晶仅在液滴撞击区域内发生黏附,黏附收集系数极限与水滴的撞击极限相同。从图10(b)可看出来流总温15 ℃冰晶融化,冰晶撞击收集系数峰值与黏附效率均增大,故其黏附收集系数的峰值增大;冰晶黏附收集系数极限与冰晶撞击极限一致。如图10(c)所示,来流总温为35 ℃时,冰晶进一步融化,此时融化导致的黏附效应占主导,黏附效率值趋于1,故冰晶撞击收集系数曲线与冰晶黏附收集系数曲线接近。由图10(d)可知,冰晶黏附收集系数峰值与极限随着来流总温的升高呈增大趋势。分析表明冰晶融化对冰晶黏附有显著影响。 针对混合相条件下,来流云雾参数对冰晶黏附效率和黏附收集系数产生的影响展开研究与讨论。 由于不同来流总温条件下,冰晶融化程度存在差异,这对冰晶黏附收集系数结果产生影响。为去除该影响因素,参照表2中算例1设置工况参数,来流总温取−5 ℃保持不变,但改变来流LWC和IWC值 设 置 算 例9:LWC = 0.3 g/m3,IWC = 0.3 g/m3;算 例10:LWC = 0.3 g/m3,IWC = 0.7 g/m3;算 例11:LWC = 0.7 g/m3,IWC = 0.3 g/m3;算 例12:LWC = 0.7 g/m3,IWC = 0.7 g/m3;并进行数值实验。 4种工况下计算结果中冰晶撞击上极限弧面坐标值均为0.052 68。冰晶黏附上极限弧面坐标值均为0.037 2,这是由于冰晶均未融化,冰晶黏附极限均与水滴撞击极限一致。表4给出撞击与黏附收集系数峰值的对比结果。 表4 不同来流云雾条件下收集系数曲线主要特征对比(算例9~算例12)Table 4 Comparison of main characteristics of collection coefficient under different conditions of cloud field (Case9-Case12) −5 ℃来流总温下冰晶黏附效率和冰晶黏附收集系数计算结果如图11所示。图11显示,随着LWC/TWC比值增大,冰晶黏附效率和黏附收集系数峰值逐渐增大。当LWC/TWC值一定时(算例9与算例12),在来流总温一致的情况下,冰晶将有着同样的黏附效率和黏附收集系数。这是因为冰晶不融化时,黏附效率取决于撞击壁面处水滴质量分数大小。 为进一步研究冰晶融化时LWC和IWC对冰晶黏附效率与冰晶黏附收集系数的影响,来流其余参数设置参照算例9~算例12,改变来流总温为15 ℃,分别对算例13~算例16进行数值实验。 算例13~算例16计算结果中冰晶撞击上极限与冰晶黏附上极限的弧面坐标值均为0.073 93,这是由于4种工况下冰晶均融化,冰晶黏附极限均与冰晶撞击极限一致。表5给出了收集系数曲线特征对比。 图12给出了15 ℃条件下不同IWC与LWC下冰晶黏附效率和黏附收集系数的计算结果。如图12(a)所示,除算例15外,其余算例的黏附效率曲线差距很小,整体保持在0.4左右,算例15中靠近翼型前缘位置冰晶黏附效率相较于其他算例明显增高,由图12(b)可得相似结果;此外,图中各算例的冰晶黏附收集系数曲线极限均与冰晶撞击收集系数极限一致。 图11 来流总温−5 ℃不同云雾参数下黏附效率与黏附收集系数Fig. 11 Sticking efficiency and catching coefficient with different cloud field parameters of total temperature of incoming flow −5 ℃ 表5 不同来流云雾条件下收集系数曲线主要特征对比(算例13~算例16)Table 5 Comparison of main characteristics of collection coefficient under different conditions of cloud field (Case13-Case16) 图12 来流总温15 ℃不同云雾参数下黏附效率与黏附收集系数Fig. 12 Sticking efficiency and catching coefficient with different cloud field parameters of total temperature of incoming flow 15 ℃ 由于来流总温为15 ℃时冰晶融化,冰晶黏附收集系数极限范围与冰晶撞击收集系数一致。对于算例15外的算例,撞击水滴的质量分数较小,冰晶融化导致的黏附效应占主导,故具有相同的黏附效率曲线和黏附收集系数曲线;而算例15的来流LWC/TWC值较大,在翼型前缘位置附近收集到的液态水滴质量分数较高,水滴对应 黏 附 效 率(εs,d)大 于 冰 晶 融 化 对 应 黏 附 效 率(εs,c),故在该区域冰晶黏附效率和黏附收集系数相较于其余算例有明显增高。 基于NNWICE平台,对冰晶/混合相结冰过程中冰晶运动相变与黏附的计算方法与影响因素开展了研究,得到以下结论: 1) 建立了拉格朗日框架下冰晶运动-传热传质耦合的数值计算方法,分析了冰晶几何形状对冰晶运动相变特性的影响,发现同粒径条件下类似柱状的长椭球状冰晶相较于扁椭球状冰晶和六角平板状冰晶在运动过程中换热、融化现象更显著。 2) 分析了基于Monte Carlo方法的冰晶/混合相结冰黏附收集系数计算方法。该方法可以在考虑冰晶运动过程中质量损失的情况下,有效模拟冰晶收集系数。 3) 系统分析了来流温度等云雾参数对冰晶黏附特性的影响。来流总温升高,冰晶融化率增加,撞击表面微元液态水质量分数增大,冰晶更易黏附;来流LWC/TWC增大,撞击表面微元液态水质量分数增大,冰晶更易黏附。2 冰晶运动相变特性
2.1 冰晶形状对运动轨迹的影响

2.2 冰晶形状对冰晶融化率的影响
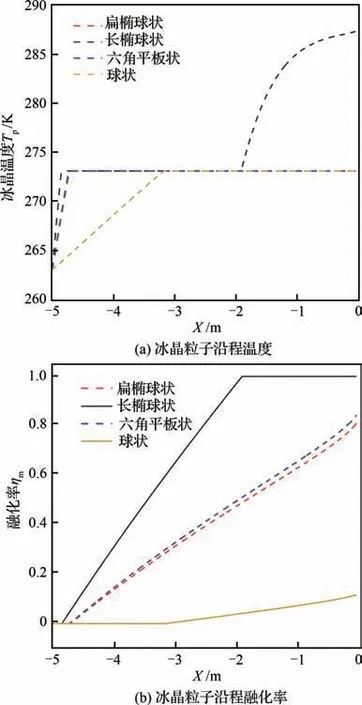
3 冰晶黏附特性
3.1 来流温度对黏附特性的影响

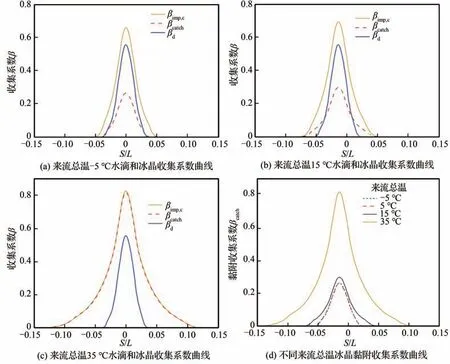
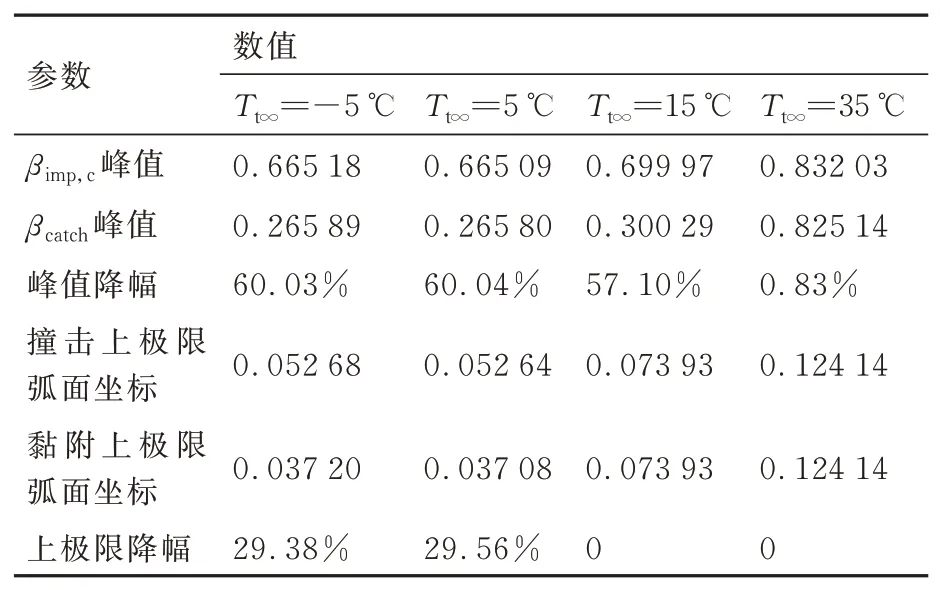
3.2 来流IWC和LWC对黏附特性的影响
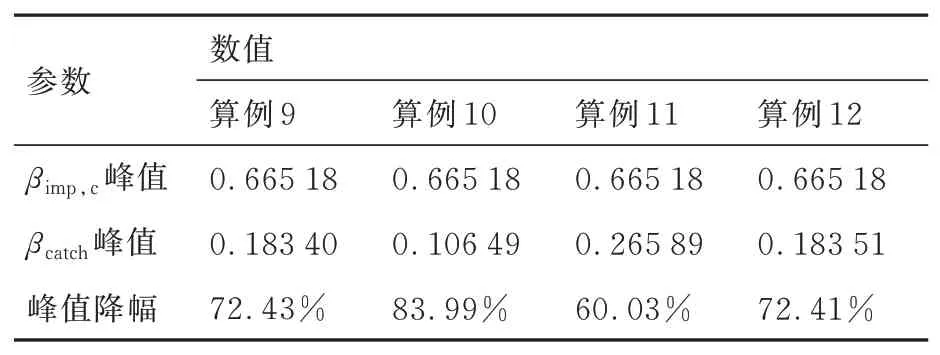
4 结 论

