强度尺度分解方法在气候温度场检验中的应用
李娟 曾晓东, 3 陈红 蔡其发
强度尺度分解方法在气候温度场检验中的应用
李娟1, 2曾晓东1, 2, 3陈红1蔡其发1
1中国科学院大气物理研究所国际气候与环境科学中心,北京100029;2中国科学院大学,北京100049;3南京信息工程大学气象灾害预报预警与评估协同创新中心,南京210044
本文首次将Casati等提出的强度尺度分解方法应用到气候地表温度场的检验中,探讨此方法用于评估气候模拟场误差的详细空间信息的适用性。以新一代气候系统模式模拟的月平均地表温度为例,传统的统计分析方法(较为常用的是空间相关系数和均方根误差、EOF分析等)不能完全反映模拟场误差的空间信息;强度尺度分解方法可计算不同阈值和空间尺度上的均方误差和模拟技巧,评估对应的模拟能力,定量给出模拟场主要误差的空间信息(误差范围即温度阈值及对应的空间尺度),例如,亚洲东部地区1月单年及多年平均的模拟场在230 K阈值1600 km模拟技巧非常低。本研究表明强度尺度分解方法适用于气候温度场的检验评估,能定量给出误差的空间信息。
强度尺度分解方法 空间检验 地表气温
1 引言
在对气候模式模拟空间场的检验评估中,常用的方法包括目测比较分析和数据统计分析。通常情况下,目测比较模拟场和观测场以及两者差值的空间分布,可抓住物理量场的整体特征及空间结构特征,大致了解模式的总体模拟能力和存在的误差,但是具有主观性和非定量性。为了定量地评估模式模拟的空间场空间分布特征的总体模拟能力,常采用的方法是数据统计分析方法,多是基于点对点的对比,利用列联表定义一系列评分指数来评估模拟能力,其结果多是一个单值来定量表现两物理量场之间的误差、线性关系等。较简单常用的有空间相关系数(皮尔逊相关系数)和均方根误差等,但均存在一定的局限性(Briggs and Levine,1997)。空间相关系数描述了两图线性相关程度,但是不能反映误差的绝对大小,例如,对一个二维场同该场乘以一个常数后进行比较,得到的相关系数是1,不能够区分两个场的差异。均方根误差反映了两场误差幅度的平均状态,但是忽略了两场的线性相关性。特别是当模拟对象发生位置偏移时,上述方法会发生“双重惩罚”问题(Jolliffe and Stephenson, 2003)。这些方法虽然能一定程度上定量给出模式模拟的空间场空间分布特征的总体模拟能力,但是不能具体反映空间信息,甚至产生与目测比较相左的结论。另外,EOF分解能够把随时间变化的变量场分解为各正交模态的独立演变过程。模态上每个点上值的大小表示这个点的变化,值越大则可以理解成这个点特别活跃,总是跳离平均值特别远,其正负没有绝对的意义,只表示相对的正反位相。EOF分解很容易将变量场的信息集中在几个模态上,并且分离出的模态结构也有一定的物理意义,但是其反映的是空间点上物理量的变化,反映不了物理量本身的空间结构。
近年来针对天气预报检验发展了很多新的创新方法(例如空间检验方法等),本文所使用的强度尺度分解方法就是天气预报空间检验方法中尺度分离法中的一种,由Casati et al.(2004)提出,主要是针对定量降水预报(QPFs)的检验。该方法不仅能够在不同的空间尺度上(例如,大尺度锋面降水和小尺度对流降水)进行检验,而且能够对不同的预报强度进行评估。主要是用不同的强度阈值对降水进行分级得到不同降水等级上的二进制误差场,并应用Haar小波进行尺度分离得到不同空间尺度成员,在此基础上计算各个空间尺度上的预报误差信息以及预报技巧。不同的空间尺度事件对应着不同的物理过程,了解了各空间尺度上的预报能力就能够更加深入地对模式中各物理过程的预报能力进行评判。Casati(2010)又对该方法进行了改进,采用了更加标准的小波分解步骤,解决了该方法在使用中发现的一些问题:首先,去除了预处理和校准数据部分,采用有偏预报场;增加了能量以及能量百分比的概念,用于评估偏差和尺度结构;增加了业务运行聚合方法以及去除二阶检验区域约束的不同方法。Mittermaier(2006)应用该方法研究表明,云可分辨尺度模式相对于对云采用参数化的粗分辨率模式提升了强降水的预报能力;Csima and Ghelli(2008)将其加入到评估业务降水预报的检验中,对业务降水预报能力进行了长期评估;孔荣等(2010)将强度尺度检验技术应用于“世界气象组织天气研究计划—北京奥运会预报示范项目”中4个邻近预报参加系统的1 h定量降水预报检验;徐同等(2012)将该技术应用于上海区域中尺度模式的定量降水预报检验。
气候场与天气场有着本质的区别,它是在某一时间段内大量天气过程的综合平均,不仅包括这段时间经常发生的天气状况,还包括偶尔出现的极端天气状况,一般比较稳定。Wang et al.(2009)提出尽管天气预报检验和气候模拟评估之间有较大差异,还是可以将天气预报检验的新方法(特别是空间检验方法和概率预报集合检验方法等)应用到气候模拟评估中,主要包括可以将这些方法应用在气候平均模拟场、季节或年际预测、多时间序列分解得到的模态评估中等。本文就是尝试将强度尺度分解方法应用到气候系统模式模拟的地表温度场的检验评估中,定量给出模拟误差场的空间信息,这方面的研究还比较少见。强度尺度分解方法(Casati et al., 2004; Casati, 2010)采用的Haar小波是非连续性的,因此其较适用于非连续场(如降水场)的检验。Picart et al.(2012)将该方法应用到了连续场的检验中,对海表面温度和叶绿素a场进行了检验。其主要是在阈值的选取方面采用了百分位方法,依据比较数据的统计分布而设定,不需要对被分析的数据有预先的了解,比较了场的内在空间结构。
本文采用绝对阈值的选取方法,首次尝试将强度尺度分解方法应用到气候地表温度模拟场的检验评估中,并检验此方法的适用性。首先进行个例检验,采用目测比较、数据统计分析、强度尺度分解三种方法分别对1982年1月检验区域的月平均地表温度场进行检验,介绍强度尺度分解方法的具体应用,比较三种方法的不同特点。其次,介绍强度尺度分解方法在多年预报检验中的应用方法。最后将强度尺度分解方法应用在不同检验区域不同月份的预报检验中,进一步验证该方法的适用性。
2 强度尺度分解方法原理
2.1 二进制误差分解
强度尺度分解方法是在不同的强度阈值和不同的空间尺度上对模拟场进行模拟技巧评估,其要求检验区域必须是正方形二阶区域(即区域格点为2×2,取正整数)。对于观测场I和模拟场I,首先要根据自身需求选择强度分级阈值,可采用绝对阈值选取法(直接选取)或百分位选取法(相当于订正后选取)等。文中需要对气候系统模式模拟结果进行直接评估,故采用了绝对阈值选取法。然后应用阈值将观测场和模拟场分别转换为二进制场:

二进制误差场被定义为二进制的模拟场减去二进制的观测场,即:

最后对二进制误差场进行二维离散Haar小波分解(Casati et al., 2004)。以检验区域格点为2×2为例,通过Haar小波分解后可以得到+1个不同空间尺度成员。这些空间成员=1, 2, 3,…,+1所对应的分辨率分别是2−1=1, 2, 4,…, 2个格点。分解过程如下:首先对原始图进行一级滤波,得到四个部分,分别是水平和垂直方向的低频成分;水平方向的低频成分和垂直方向的高频成分;水平方向的高频成分和垂直方向的低频成分;水平方向和垂直方向的高频成分。其中,水平和垂直方向的低频成分经过二维Haar离散小波逆变换成为第一父小波成员,剩下的包含有高频成分的三个部分分别进行二维Haar离散小波逆变换,得到三个重构场,将这三个重构场相加获得第一母小波成员(即第一个空间尺度成员);然后对第一父小波成员重复以上的操作,可以得到第二母小波成员以及第二父小波成员;以此类推最后得到个母小波成员和第+1父小波成员(整个区域的平均值),即+1个不同空间尺度成员。另外由于二维离散Haar小波变换是正交的,因此得到的各空间尺度成员也是正交的,这是该方法的一个主要特征。二进制误差场可以用二维离散小波分解后的成员和表示:

2.2 二进制均方误差
均方误差定义为各模拟值误差的平方和的平均值,将不同阈值和不同空间尺度上的均方误差表示为E,l,可以用来评估模式对各强度阈值在不同空间尺度上的模拟误差。由于离散小波的正交性,那么不同空间尺度上的均方误差之和就等于原始二进制场上的均方误差,即:

对于每一个强度阈值,还可以计算各个空间尺度对总的均方误差E的贡献率,即:

2.3 强度尺度技巧评分
仅使用均方误差来评估模拟技巧会出现问题。比如,大尺度模拟对象发生小的位置偏差和小尺度模拟对象发生大的位置偏差,计算的均方误差值可能一样,但是前者的技巧明显应该高一些。因此,Casati设计了强度尺度技巧评分。首先评估随机产生的二进制误差场的均方误差期值Erand,

其中,为偏差,即模拟发生数与观测发生数的比值;为击中率,即观测发生数占总网格数的比。其次将Erand均分到+1个尺度上,得到强度尺度技巧评分:
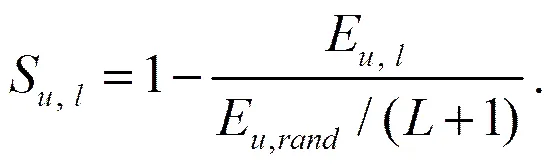
因此,可以对各强度阈值在不同空间尺度上的模拟技巧进行评估。S为正值时,阈值尺度上模拟的均方误差小于该阈值该尺度上的均方误差期值,表示有模拟技巧;反之,S为负值时,则模拟的均方误差大于均方误差期值,无模拟技巧。
3 强度尺度分解方法在模拟评估中的应用
3.1 数据说明及区域选择
本文应用的数据是中国科学院大气物理研究所研发的新一代气候系统模式的模拟产品,水平分辨率为1°×1°,记为CSM。其中,大气环流模式采用具有较高分辨率且物理过程完善的新一代大气环流模式IAP-AGCM(张贺等,2009;孙泓川等,2012;Zhang et al.,2013;Su et al.,2014;Yan et al.,2014);大洋环流模式采用第三代全球海洋模式LICOM(Liu et al.,2004,2012);陆面过程模式是改进的通用陆面过程模式CLM3.0(Dickinson et al.,2006)。观测数据采用CRU和NECP再分析资料的混合产品,记为CRUNCEP (http://www.cesm.ucar. edu/models/cesm1.2/ clm/clm_ forcingdata_ esg. html [2016-05-06])。该数据分辨率为0.5°×0.5°,文中将其线性整合为1°×1°。选取1月份的月平均地表温度数据进行比较,时间范围为1982~2010年,检验区域为亚洲东部(15°N~78°N,97°E~160°E),格点为64×64;作为对照,另选取1982年6月份的月平均地表温度数据进行比较,检验区域为亚洲东北部(43°N~74°N,87°E~118°E),格点为32×32。
3.2 气候态及个例检验分析
本节首先应用目测比较分析方法对气候系统模式CSM模拟的1982~2010年检验区域的1月份地表温度气候态以及1982年1月月平均的整体模拟情况和存在的误差有个大致的了解,并以1982年1月月平均地表温度为例,应用统计分析方法和强度尺度分解方法进行模拟评估,比较两方法的评估结果,检验强度尺度分解方法是否能够定量自动地得出目测比较方法所了解到的模拟误差的空间信息。
图1a–c给出了1982~2010年1月份地表温度气候态CSM模式模拟与CRUNCEP观测对比以及误差。观测图中温度从南到北呈带状分布,并且 海陆差异明显,同一纬度海洋温度明显比陆地要高。模式模拟出了南北带状分布以及明显的海陆差异,但是海洋温度整体比观测偏高,中低纬的陆地地表温度与观测较为一致,最大差异出现在了高纬俄罗斯东北部区域,观测数据在该区域大部地区的温度在230 K以下,而模拟值偏高,没有230 K温度线。1982年1月的情况与气候态大致一致(图1d–f),观测数据在俄罗斯东北部区域有了更大范围的230 K线,甚至出现了220 K线,而模拟的230 K线范围明显偏小,模拟值偏大。下面以1982年1月月平均地表温度模拟检验评估为例,对比统计分析方法和强度尺度分解方法的评估结果,考察强度尺度分解方法的适用性。

图1 (a)CSM模式模拟的气候态地表温度;(b)CRUNECP观测的气候态地表温度;(c)模式模拟与观测的气候态地表温度之差。(d)、(e)、(f)同(a)、(b)、(c),但为1982年1月平均的地表温度。单位:K

图2 粗阈值各空间尺度上的强度尺度技巧评分:(a)1982年;(b)气候态
3.2.1 统计分析方法
本节所采用的统计分析方法是空间相关系数和均方根误差RMSE,公式如下:


其中,是模拟场,是观测场,是检验区域的格点个数。空间相关系数用于衡量模拟场和观测场的线性相关程度,取值范围为[−1,1]。均方根误差用于表述检验区域内误差幅度的平均情况。
理想的检验评分系统应该包含充足的信息,并且能够通过这些检验结论重构出模拟和观测场的分布。但这些方法都是基于点对点的检验,不能反映场的空间信息。通过计算得出1982年1月CSM模式模拟的月平均地表温度场与CRUNCEP观测场的空间相关系数=0.9767(气候态=0.9844),均方根误差RMSE=5.95(气候态RMSE=4.72)。从两个数值可以看出两个场具有较高的正相关,误差较大,但对于目测比较的结论230 K模拟范围有较大的误差则无从反映。
3.2.2 强度尺度分解方法
强度尺度分解方法所分离的各尺度空间成员并不与原始场相似,但将各尺度空间成员相加能够组合成原始场。其能够评估模式不同强度阈值在不同空间尺度上的模拟能力,得到各阈值各尺度上的均方误差大小以及模拟技巧,反映出一些误差场的空间信息。
首先根据图1中观测场和模拟场的取值范围,采用绝对阈值选取法均匀地确定分级阈值为220、230、240、250、260、270、280、290、300 K(称粗阈值)。检验区域格点数为64×64(即26×26),因此可以分离出7个不同的空间成员。模式空间分辨率1°,约等于100 km,故前6个空间尺度分别对应为100、200、400、800、1600、3200 km。图2给出了各阈值各空间尺度上的强度尺度技巧评分(图2a为1982年,图2b为气候态)。从图2a中可以看出:中间阈值240~290 K的评分值在各个空间尺度上都为正,说明他们都有模拟技巧。目测290 K线模拟比观测明显偏北,但其各个空间尺度上的评分却都为正,主要原因就是其均方误差期值(0.3193)较大,但在尺度3和尺度4上的评分相对其他尺度上的评分还是明显低的,也相应反映了该阈值误差的尺度范围。而在高温和低温两极的评分值在个别尺度上则出现了负值,即无模拟技巧。特别是阈值230 K在尺度5上出现了一个很明显的负值,说明对230 K的模拟在尺度5上误差较大,无模拟技巧,这与目测比较的结论相同(这一特点在气候态的检验结果中也比较明显,见图2b)。阈值220 K和230 K的均方误差期值都比较低,较容易产生负值区域。

图3 阈值230 K时的模拟与观测的二进制误差场
下面进一步分析阈值230 K在尺度5上误差最大的原因。图3给出了温度阈值230 K时的模拟与观测二进制误差场。可以看出模拟过多地模拟了230 K以上的温度区域,这个误差区域在经向上最大宽度范围是60°N~73°N,大约为1300 km。图4给出了该二进制误差场经由二维离散Haar小波分解后获得的母小波成员误差图,表1给出了各尺度上的均方误差、对总均方误差的贡献率、技巧评分。可以看出尺度5(约等于1600 km)的均方误差最大,贡献率达到了30%多,技巧评分−0.9796。定量地说明原始二进制误差场上误差范围的尺度大约在1600 km左右,这与实际情况1300 km很接近。

图4 230 K阈值时二进制误差场经由二维离散Haar小波分解后获得的母小波成员
将230 K附近的阈值进行加密得到各尺度上的强度尺度技巧评分(图5)。可以看到阈值225~231 K在尺度5上的技巧评分值都是负的,无技巧评分。特别要注意的是,当阈值为225 K,在尺度4上的技巧评分最低,远低于尺度5的评分,说明阈值为225 K时误差范围的尺度大约应该是在尺度4上(约等于800 km)。从各阈值各尺度上的均方误差E,l柱状图中也可以看出阈值228~231 K在尺度5上的均方误差最大,阈值225 K尺度4的均方误差最大(图略)。图6分别给出了阈值225、228、229、230、231、235 K的模拟与观测二进制误差场。从图中可以看出阈值225 K的误差范围明显比其他阈值的误差范围小很多,其经向最大宽度范围是60°N~69°N,大约为900 km。阈值228~231 K的误差区域经向最大宽度范围大约是在1300 km。强度尺度检验方法的结论与其基本一致,说明该方法能够定量地给出误差范围的大小。

图5 加密阈值各空间尺度上的强度尺度技巧评分
3.3 强度尺度分解方法在多年模拟检验中的应用
应用强度尺度分解方法对CSM气候系统模式模拟的29年(1982~2010年)逐年的1月份月平均地表温度数据与相应的CRUNCEP数据进行了比较分析。在相同的检验区域上进行了粗阈值分尺度比较,结果发现大多数年份模拟阈值为230 K的误差在尺度5上都比较大,模拟技巧评分相对较低。由于技巧评分本身不是线性的,因此反映29年的技巧评分情况不能够简单地进行平均。本文采用盒须图,分别表示出了技巧评分在这29年中最低、25%分位、中分位、75%分位、最高的技巧评分值。图7给出了阈值230 K时在不同空间尺度上的盒须图。图中下引线的最低点代表的是29年中所得到的技巧评分最小值;上引线的最高点代表的是最大值;中间盒子底线、顶线和中位线分别是25%分位、75%分位和50%分位所对应的技巧评分值。从图中可以看出:尺度5上的盒子主体值以及中分位值都明显低于其他尺度,说明模拟误差主要是在尺度5上。另外尺度1下引线的最低点达到了−1.95,这是因为1991年1月北方整体温度偏高(观测图略),230 K范围在多年中最小,达不到更大的尺度。

表1 阈值230 K时各尺度上的检验指标

图7 阈值230 K时不同空间尺度上的盒须图(1982~2010年)
3.4 强度尺度分解方法在不同区域不同月份的检验应用
图8给出了1982年6月CSM模式模拟的月平均地表温度与CRUNCEP观测的对比。模式模拟的基本分布形势与观测相似,温度高低中心位置和强度与观测基本一致,主要误差是模式模拟的280 K线比观测偏北约700 km。应用强度尺度方法在280 K附近加密阈值得到各空间尺度的技巧评分(图9),其中阈值278~280 K的空间尺度4上都有明显的负值,无模拟技巧,误差尺度约为800 km,定量地表达了目测检验结果。

图8 1982年6月的月平均地表温度(单位:K):(a)CSM模式模拟;(b)CRUNECP观测;(c)模拟与观测之差
4 总结和讨论
本文首次尝试将强度尺度分解方法应用到气候系统模式模拟的地表月平均温度的检验评估中,讨论气候模拟场误差的详细空间信息,从中得到以下几点结论:
(1)以1982年1月(亚洲东部)为例,应用三种方法分别对检验区域的地表月平均温度模拟场进行评估,可以得出:目测比较明显看出模拟场230 K范围线与观测场有较大的误差,经向方向的误差范围大约是在1300 km左右;统计分析方法仅能得出两个场具有较高的正相关,误差较大,无从反映误差场的空间信息;应用强度尺度分解方法后,可以发现230 K阈值在尺度5(大约1600 km)上模拟技巧非常低,定量地反映了误差场的空间信息,与目测结论基本一致。
(2)应用强度尺度分解方法对相同检验区域相同月份1982~2010年29年的模拟情况进行检验评估分析,发现在这29年中大部分年份都出现了与1982年相似的误差空间信息,即230 K阈值在尺度5(大约1600 km)上模拟技巧相对其他尺度明显低。这个误差在29年中大部分年份都出现了,说明模式对这个区域的模拟有待改进。
(3)改变检验区域和检验月份,通过强度尺度分解方法也定量得到了与目测比较相一致的误差空间信息。
需要指出的是,强度尺度分解方法中用到的Haar小波是非连续的,因此适合于非连续场(如天气过程的降水场)的检验,通过对不同强度阈值不同空间尺度成员进行评估,从而分离出并客观定量评价中尺度降水和对流性降水的预报效果,特别是能够很好地表达预报对象位置偏移误差及其大小。而气候温度场是连续场,本文工作表明Haar小波同样也可用于该连续场的检验,但是否存在更适合于温度场检验的子波尚有待于进一步研究。此外,降水场本身具有不同空间尺度的物理过程,不同尺度的模拟差异可能主要体现对应的降水参数化方案的结果。与之相比,地表温度场不仅在纬度上具有显著梯度变化,而沿经度方向大尺度特征则一般反映海洋性与大陆性气候差异,而在局部的空间结构则体现陆表特征(如地形、植被分布等)差异,因而对气候温度场的检验反映的是上述多因素共同作用的复杂结果。强度尺度分解方法采用的温度强度阈值及尺度,一般而言没有普适的物理意义,因此需要针对具体问题对于误差结果进行分析。例如,本文研究的对东北亚区域1982年1月的模拟情况,去除该区域平均偏差的整体影响后,误差相对于实况值的散点分布图显示模式在实况(CRUNCEP)温度240~290 K的误差有正有负,但在实况230 K以下误差基本为正(图略),表明模式在该区域对230 K以下温度模拟存在系统偏差。具体分析发现,实况中230 K以下温度分布区域中心大陆南北方向较窄,同时地势相对较高。而230 K阈值下对应的误差空间尺度5,主要反映实况场低温区温度分布的空间尺度,模拟场在这个地方没有模拟出低于230 K的低温区。模式研发及评估人员可利用这些信息,从模式对主要物理过程及模式方案(如海陆相互作用、复杂地形影响、大气环流场的描述等)方面,分析模式产生上述偏差的原因。另一方面,如果将强度尺度分解方法应用于逐日的温度场分析时,还可能出现模式模拟的温度场中心区域出现一定偏差,此时误差对应的空间尺度主要体现为模拟场与实况场的空间偏移。

图9 加密阈值各空间尺度上的强度尺度技巧评分
在使用强度尺度分解方法进行温度场研究时,Picart采用百分位阈值选取方法生成非连续的空间结构场。固定百分位间隔使得各百分位阈值的检验格点个数一样,其所对应的绝对阈值分布范围却不均。检验格点个数一样,则=1,等于百分位间隔,各百分位阈值的均方误差期值E, rand就是一个常数,计算技巧评分时就仅跟E, l有关。由于一般情况下,中间百分位绝对阈值的分布范围要小于两边百分位绝对阈值的分布范围,因此中间百分位的技巧评分会低于两边百分位的技巧评分(Kwiatkowski et al., 2014)。同时百分位的选取方法本身就是进行了一次订正再进行评估,因此该方法适用于对中短期气候预测等的诊断评估(这些预测常对模式模拟的结果进行后处理以排除系统误差)。而绝对阈值选取方法是将温度场转换为非连续的空间分布场。各绝对阈值的检验格点个数不同,计算技巧评分时与E, l和E, rand都有关。由于E, rand在中间绝对阈值时较大,在两边极值时较小,因此如本文所示,通常两边极值的技巧评分会相对差些。该方法适用于耦合模式(如气候系统模式、地球系统模式等)的误差诊断分析,因为在这些系统中不同分系统模式之间有大量数据传递,需要对各分系统的模拟结果进行直接检验。
Briggs W M, Levine R A. 1997. Wavelets and field forecast verification [J]. Mon. Wea. Rev., 125 (6): 1329–1341, doi:10.1175/1520-0493(1997)125< 1329:WAFFV>2.0.CO;2.
Casati B, Ross G, Stephenson D B. 2004. A new intensity-scale verificaton approach for the verification of spatial precipitation on forecasts [J]. Meteor. Appl., 11 (2): 141–154, doi:10.1017/S1350482704001239.
Casati B. 2010. New developments of the intensity-scale technique within the spatial verification methods intercomparison project [J]. Wea. Forecasting, 25 (1): 113–143, doi:10.1175/2009WAF2222257.1.
Csima G, Ghelli A. 2008. On the use of the intensity-scale verification technique to assess operational precipitation forecasts [J]. Meteor. Appl., 15 (1): 145–154, doi:10.1002/met.49.
Dickinson R E, Oleson K W, Bonan C, et al. 2006. The community land model and its climate statistics as a component of the community climate system model [J]. J. Climate, 19 (11): 2302–2324, doi:10.1175/JCLI3742.1.
Jolliffe I T, Stephenson D B. 2003. Forecast Verification: A Practitioner’s Guide in Atmospheric Science [M]. New York: Wiley and Sons, 240pp.
孔荣, 王建捷, 梁丰, 等. 2010. 尺度分解技术在定量降水临近预报检验中的应用 [J]. 应用气象学报, 21 (5): 535–544. Kong Rong, Wang Jianjie, Liang Feng, et al. 2010. Applying scale decomposition method to verification of quantitative precipitation nowcasts [J]. J. Appl. Meteor. Sci. (in Chinese), 21 (5): 535–544, doi:10.11898/1001-7313.20100503.
Kwiatkowski L, Halloran P R, Mumby P J, et al. 2014. What spatial scales are believable for climate model projections of sea surface temperature? [J] Climate Dyn., 43 (5–6): 1483–1496, doi:10.1007/s00382-013-1967-6.
Liu Hailong, Zhang Xuehong, Li Wei, et al. 2004. An eddy-permitting oceanic general circulation model and its preliminary evaluation [J]. Adv. Atmos. Sci., 21 (5): 675–690, doi:10.1007/BF02916365.
Liu Hailong, Lin Pengfei, Yu Yongqiang, et al. 2012. The baseline evaluation of LASG/IAP climate system Ocean Model (LICOM) version 2 [J]. Acta Meteor. Sinica, 26 (3): 318–329, doi:10.1007/s13351-012- 0305-y.
Mittermaier M P. 2006. Using an intensity-scale technique to assess the added benefit of high-resolution model precipitation forecasts [J]. Atmos. Sci. Lett., 7 (2): 36–42, doi:10.1002/asl.127.
Picart S S, Butenschön M, Shutler J D. 2012. Wavelet-based spatial comparison technique for analysing and evaluating two-dimensional geophysical model fields [J]. Geosci. Model Dev., 5 (1): 223–230, doi:10.5194/gmd-5-223-2012.
Su Tonghua, Xue Feng, Zhang He. 2014. Simulating the intraseasonal variation of the East Asian summer monsoon by IAP AGCM4.0 [J]. Adv. Atmos. Sci., 31 (3): 570–580, doi:10.1007/s00376-013-3029-8.
孙泓川, 周广庆, 曾庆存. 2012. IAP第四代大气环流模式的耦合气候系统模式模拟性能评估 [J]. 大气科学, 36 (2): 215–233. Sun Hongchuan, Zhou Guangqing, Zeng Qingcun. 2012. Assessments of the climate system model (CAS-ESM-C) using IAP AGCM4 as its atmospheric component [J]. Chinese Journal of Atmospheric Sciences (in Chinese), 36 (2): 215–233, doi:10.3878/j.issn.1006-9895.2011.11062.
Wang Bin, Xie Xin, Li Lijuan. 2009. A review on aspects of climate simulation assessment [J]. Adv. Atmos. Sci., 26 (4): 736–747, doi:10. 1007/s00376-009-9038-y.
徐同, 戴建华, 李佳, 等. 2012. 强度尺度方法在模式定量降水预报检验中的应用 [J]. 气象与环境科学, 35 (1): 1–7. Xu Tong, Dai Jianhua, Li Jia, et al. 2012. Applying intensity-scale approach to verification of model quantitative precipitation forecast [J]. Meteor. Environ. Sci. (in Chinese) 35 (1): 1–7, doi:10.3969/j.issn.1673-7148.2012.01.001.
Yan Zhengbin, Lin Zhaohui, Zhang He. 2014. The relationship between the East Asian subtropical westerly jet and summer precipitation over East Asia as simulated by the IAP AGCM4.0 [J]. Atmos. Oceanic Sci. Lett., 7 (6): 487–492, doi:10.3878/AOSL20140048.
张贺, 林朝晖, 曾庆存. 2009. IAP AGCM-4动力框架的积分方案及模式检验 [J]. 大气科学, 33 (6): 1267–1285. Zhang He, Lin Zhaohui, Zeng Qingcun. 2009. The computational scheme and the test for dynamical framework of IAP AGCM-4 [J]. Chinese Journal of Atmospheric Sciences (in Chinese), 33 (6): 1267–1285, doi:10.3878/j.issn.1006-9895. 2009.06.13.
Zhang He, Zhang Minghua, Zeng Qingcun. 2013. Sensitivity of simulated climate to two atmospheric models: Interpretation of differences between dry models and moist models [J]. Mon. Wea. Rev., 141(5): 1558–1576, doi:10.1175/MWR-D-11-00367.1.
李娟, 曾晓东, 陈红, 等. 2016. 强度尺度分解方法在气候温度场检验中的应用[J]. 大气科学, 40 (6): 1117–1126. Li Juan, Zeng Xiaodong, Chen Hong, et al. 2016. Application of the intensity-scale technique for verification of climatological surface temperature simulation [J]. Chinese Journal of Atmospheric Sciences (in Chinese), 40 (6): 1117–1126, doi:10.3878/j.issn.1006-9895.1603.15180.
Application of the Intensity-Scale Technique for Verification of Climatological Surface Temperature Simulation
LI Juan1, 2, ZENG Xiaodong1, 2, 3, CHEN Hong1, and CAI Qifa1
1,,,1000292,1000493,,210044
The applicability of the intensity-scale approach for the verification of climate simulation is investigated in this paper. The monthly mean surface temperature simulated by a new generation of climate system model is taken as an example. While the traditional statistical verification cannot fully reflect the spatial information of the simulation error, the intensity-scale approach can quantitatively assess the spatial information of the simulation by calculating the mean square errors and skill scores of the spatial components with different wavelet scales and intensities. For example, in East Asia, the skill score of temperature threshold 230 K and spatial scale 1600 km is very low for simulations of both January of single year and multi-year average. This study shows that the intensity-scale approach is suitable for the verification of climatological temperature simulation, and can provide quantitative spatial information of the error.
The intensity-scale approach, Spatial verification, Surface temperature
1006-9895(2016)06-1117-10
P468
A
10.3878/j.issn.1006-9895.1603.15180
2015-04-09;网络预出版日期 2016-03-30
李娟,女,1981年出生,博士研究生,主要从事数值天气预报和产品检验方面的研究工作。E-mail: lijuan@mail.iap.ac.cn
曾晓东,E-mail: xdzeng@mail.iap.ac.cn
中国科学院战略性先导科技专项XDA05110103
Chinese Academy of Sciences Strategic Priority Research Program (Grant XDA05110103)

