L-双拓扑空间的LFα-p连通性的若干性质
徐小玲, 马保国 , 孙军娜
(延安大学西安创新学院 ,西安710100)
L-双拓扑空间的LFα-p连通性的若干性质
徐小玲1, 马保国2,孙军娜2
(延安大学西安创新学院 ,西安710100)
文[1]首先提出了L-拓扑空间中的p-开集、p-闭集等概念,本文以此为基础,引入了L-双fuzzy拓扑空间的α-p连通性的概念,并研究了其若干基本性质.
L-双fuzzy拓扑空间; α-p隔离集; α-p连通集
1 引 言
自从Kelly1963年在文[2]中讨论了双拓扑空间后,许多作者从不同的角度出发,提出了各种各样的连通性,在文献[3]中,郑崇友研究了L-双fuzzy拓扑空间中的连通性,本文在文[3]的基础上,利用p-开集、p-闭集,引入了L-双fuzzy拓扑空间中若干新的连通性——α-p连通性、弱配α-p连通性、配α-p连通性,讨论了它们之间的关系与性质,进一步推广和丰富了L-双fuzzy拓扑空间中的连通性理论.

2 预备知识
定义1[1]设(LX,δ)是L-fts,A∈LX称为p-开集当且仅当存在开集U,使得A≤U≤A-;若A是p-开集,则称A′是p-闭集.
L-fts(LX,δ)中的所有p-开集记作LPO(LX),所有的p-闭集记作LPC(LX).
L-fts中的闭集一定是p-闭集,反之一般不成立.
定理1[1]设(LX,δ)是L-fts,则
δ⊂LPO(LX),δ′⊂LPC(LX).
定义2[1]设(LX,δ)是L-fts,A,B∈LX,
(a) 包含于A的一切p-开集的并叫做A的LF-p内部,记作AΔ,即
AΔ=∨{B∈LPO(LX)|B≤A}.
(b) 包含于A的一切p-闭集的交叫做A的LF-p闭包,记作A←,即
A←=∧{B∈LPO(LX)|A≤B}.
定理2[4]设(LX,δ)是L-fts,A,B∈LX,则
(a) A°≤AΔ≤A≤A←≤A-;(b) 若A∈δ∩LPC(LX),则A∈δ′;
(c) 若A∈δ′∩LPO(LX),则A∈δ;(d) 若A≤B,则A←≤B←,AΔ≤BΔ;
(e) (A∨B)←=A←∨B←,(A∧B)Δ=AΔ∧BΔ;
(f) p-闭集的任意交是p-闭集,p-开集的任意并是p-开集.
定义3设(LX,δ)是L-fts,A,B∈LX,α∈L-{0},若A←∧B≤α′且A∧B←≤α′,则称A,B在(LX,δ)中是α-p隔离的.
定义4设(LX,δ)是L-fts,S∈LX,则不存在A,B∈LX,使得A,B在(LX,δ)中是α-p隔离的,且A∨B=S,A≤ α′,B≤ α′,则称S是(LX,δ)中的α-p连通集;特别的,当L中最大的L-fuzzy集1是(LX,δ)中的α-p连通集时,则称(LX,δ)为α-p连通空间;否则称(LX,δ)为α-p不连通空间.
定义5设(LX,δ)是L-fts,α∈L-{0},A∈LX,当β≥α′时,若lβ(A←)=lβ(A),则称A为α-p闭集,其中lα(A)={x∈X|A(x)≤ α};若A′是α-p闭集,则称A为α-p开集.
定义6设δ1,δ2都是LX上的L-fuzzy拓扑,则(LX,δ1,δ2)称为L-双fuzzy拓扑空间,简称L-bfts.
注1若对任意的α1,α2∈L-{0},都有α1∧α2≠0,则称L是正则的,本文中始终考虑L是正则的情形.
定义7设(LX,δ1,δ2)是L-bfts,S∈LX,α1,α2∈L-{0},若S既是(LX,δ1)中的α1-p连通集,又是(LX,δ2)中的α2-p连通集,则称S是(LX,δ1,δ2)中的(α1,α2)-p连通集.特别当α1=α2=α时,则称S是(LX,δ1,δ2)中的α-p连通集.若LX中的最大元1是α-p连通的,则称(LX,δ1,δ2)是α-p连通空间.
定义8设(LX,δ1,δ2)是L-bfts,A,B∈LX,αi∈L-{0} (i=1,2),若
(1)
或

(2)
则称A与B在(LX,δ1,δ2)中是弱配(α1,α2)-p隔离的.若(1),(2)同时成立,则称A与B在(LX,δ1,δ2)是配(α1,α2)-p隔离的.
定义9设(LX,δ1,δ2)是L-bfts,S∈LX,α1,α2∈L-{0},若不存在A,B∈LX,使得A与B在(LX,δ1,δ2)中是弱配(α1,α2)-p隔离的,且
A∨B=S,A≤ α′1∨α′2,B≤ α′1∨α′2,
则称S是(LX,δ1,δ2)中弱配(α1,α2)-p连通集;特别,当α1=α2=1时,则称S是(LX,δ1,δ2)中的弱配p连通集;若最大元1是弱配(α1,α2)-p连通的,则称(LX,δ1,δ2)是弱配(α1,α2)-p连通空间.
若不存在A,B∈LX,使得A与B在(LX,δ1,δ2)中是配(α1,α2)-p隔离的,且
A∨B=S,A≤ α′1∨α′2,B≤ α′1∨α′2,
则称S是(LX,δ1,δ2)中配(α1,α2)-p连通集;特别,当α1=α2=1时,则称S是(LX,δ1,δ2)中的配p连通集;若最大元1是配(α1,α2)-p连通的,则称(LX,δ1,δ2)是配(α1,α2)-p连通空间.
2 α-p连通的性质
定理3设(LX,δ1,δ2)为双满层的L-bfts,S,D∈LX,D≤S,D是弱配(α1,α2)-p连通集,α1,α2∈M(L),且

则S是(LX,δ1,δ2)中的弱配(α1,α2)-p连通集.
证假设S不是(LX,δ1,δ2)中的弱配(α1,α2)-p连通集,则存在A,B∈LX,A与B为弱配(α1,α2)-p隔离的,使得
A∨B=S,A≤ α′1∨α′2,B≤ α′1∨α′2
且

令A1=D∧A,B1=D∧B,则
D=D∧S=(D∧A)∨(D∧B)=A1∨B1,
且






所以A≤α′1∨α′2,与A≤α′1∨α′2矛盾.
因此,S是(LX,δ1,δ2)中的弱配(α1,α2)-p连通集.
定理4设(LX,δ1,δ2)为双满层的L-bfts,S,D∈LX,D≤S,D是配(α1,α2)-p连通集,α1,α2∈M(L),且

则S是(LX,δ1,δ2)中的配(α1,α2)-p连通集.
证与定理3类似,略去.

证假设S不是(LX,δ1,δ2)中的配(α1,α2)-p连通集,则存在A,B∈LX,A与B为配(α1,α2)-p隔离的,使得
A∨B=S,A≤ α′1∨α′2,B≤ α′1∨α′2
且

令A1=D∧A,B1=D∧B,则
D=D∧S=(D∧A)∨(D∧B)=A1∨B1,
且

又D是配(α1,α2)-p连通集,所以A1≤α′1∨α′2,B1≤α′1∨α′2,则由(LX,δ1,δ2)是双满层的,知


因此
=α′1∨α′2,
与A≤ α′1∨α′2矛盾.




A∨B=f(D),A≤β′1∨β′2,B≤β′1∨β′2,
且

则

令E=f-1(A),F=f-1(B),故
D≤f-1f(D)=f-1(A∨B)=E∨F,


令G=D∧E,H=D∧F,则G∨H=D,且

又D是(LX,δ1,δ2)中的配(α′1,α′2)-p连通集,因此,G≤α′1∨α′2,H≤α′1∨α′2,所以
D=G∨H≤(α′1∨α′2)∨H,
f(D)≤f(α′1∨α′2)∨f(H)=f(α′1∨α′2)∨ff-1(B)≤f(α′1∨α′2)∨f(α′1∨α′2)∨B,
A=A∧f(D)≤f(α′1∨α′2)∨(A∧B)≤f(α′1)∨f(α′2)∨β′1∨β′2=β′1∨β′2,
与A≤ β′1∨β′2矛盾!
(b) 与(a)类似,略去.

(a) 若D是(LX,δ1,δ2)中的配p连通集,则f(D)是(LX,δ1,δ2)中的配p连通集;
(b) 若D是(LX,δ1,δ2)中的弱配p连通集,则f(D)是(LX,δ1,δ2)中的弱配p连通集.
证(a) 取α1=α2=1,则D是(LX,δ1,δ2)中的配p连通集,即为配(1,1)-p连通集,且
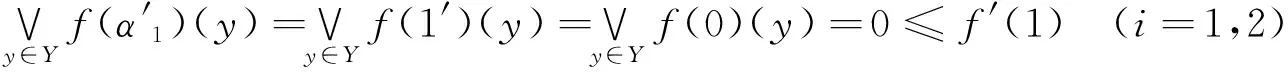
由定理6,f(D)是(LX,δ1,δ2)中的配(β1,β2)-p连通集,其中

则f(D)是(LX,δ1,δ2)中的配(1,1)-p连通集,所以f(D)是(LX,δ1,δ2)中的配p连通集.
(b) 与(a)类似,略去.
定理7设(LX,δ1,δ2)是L-bfts,α1,α2∈L-{0},则
(a) (LX,δ1,δ2)中各配(α1,α2)-p连通分支之并为1;
(b) 若S1,S2为(LX,δ1,δ2)中的两个不同的配(α1,α2)-p连通分支,则D1∧D2≤α′1∨α′2;
(c) 若S是(LX,δ1,δ2)中的配(α1,α2)-p连通分支,则S∈δ′1∧δ′2.
证(a) 任取xα∈M*(LX),则α∈M(L),α′≠1,故存在β∈M(L),β≤ α′.
令ϑ(xα)={A∈LX|xα≤A,且A为配(β1,β2)-p连通集},故A(xα)=∨ϑ(xα).

(b) 假设D1∧D2≤α′1∨α′2,由推论2.2知,D1∨D2为弱配(α1,α2)-p连通集,与D1与D2的极大性矛盾,所以,D1∧D2≤α′1∨α′2.

[1]马保国,王延军,姜金平.L-拓扑空间中的p-良紧性[J].重庆师范大学学报,2006,23(4):10-14.
[2]Kelly J C.Bitopological spaces[J].Proc.London Math.Soc,1963,13(3):71-89.
[3]郑崇友.L-双fuzzy拓扑空间论的连通性[J].北京师院学报,1990,11(4):1-6.
[4]马保国,王延军,车雨红.L-拓扑空间中的p-连通性[J].纺织基础科学学报,2008,21(4):438-441.
[5]徐国华.L-双fuzzy拓扑空间的α连通性[J].模糊系统与数学,1994,18(1):209-215.
[6]王国俊.L-fuzzy拓扑空间论[M].西安:陕西师范大学出版社,1988.
[7]徐小玲,马保国,马海红.L-双fuzzy拓扑空间的α-p连通性(Ⅰ)[J].西安:西安工程大学学报,2008,22(2):220-225.
[8]杨海龙,李生刚.L-拓扑空间的δ连通性[J].纺织基础科学学报,2006,19(3):189-192.
[9]徐小玲,马保国.L-fuzzy拓扑空间的α-p连通性(Ⅱ) [J]. 纺织高校基础科学学报. 2011,24(2):180-184.
Some Properties of LF α-p Connectedness on L- Bitopological Spaces
XUXiao-ling,MABao-guo,SUNJun-na
(Xi’an Innovation College of Yan’an University, Xi’an 710100,China)
In the paper[1],p-open sets and p-closed sets are firstly introduced in L-topological spaces.In this paper based on the notions,the concept of α-p connectedness is given in L-fuzzy bitopological spaces.Moreover,its basic properties are studied.
L-fuzzy bitopological space;α-p separated sets;α-p connected sets
2016-03-12;[修改日期]2016-04-28
徐小玲(1984-),女,硕士,讲师,从事格上拓扑学的研究.Email:17113525@qq.com
O189.1
A
1672-1454(2016)03-0044-05

