一种改进的人工蜂群算法*

刘晓芳 柳培忠 黄德天 郑 洋 黄炜钦



一种改进的人工蜂群算法*

刘晓芳 柳培忠 黄德天 郑 洋 黄炜钦

华侨大学工学院

人工蜂群算法是一种模拟蜜蜂群智能搜索行为的随机优化算法，已被成功用于解决许多优化问题。该文针对基本人工蜂群算法在收敛速度和局部寻优方面存在的缺点，提出了一种具有平衡能力的改进算法。此算法在观察蜂阶段引入惯性权重，使用随着迭代次数动态变化的惯性权重因子来平衡种群的局部搜索和全局探测能力，防止算法陷入局部最优和加快寻优速度；在侦察蜂阶段（scout bees），则利用正弦函数搜索操作，正弦函数服从均匀分布，能很好地搜索全部范围，以提高种群多样性。通过对5个基准测试函数进行仿真实验，并与原算法进行比较，结果表明，改进的算法在收敛速度和搜索精度上基本优于人工蜂群算法。

人工蜂群算法 算法改进 惯性权重因子 正弦搜索 收敛性

1 概述

人工蜂群算法（Artificial Bee Colony，ABC）[1,2]是土耳其学者Karaboga等人在2005年提出的一种比较新的群智能算法，它是模拟蜜蜂群体寻找优良食物源的方法，与遗传算法、粒子群算法、蚁群算法等智能计算方法相比，该算法的突出优点是在每次迭代中都进行全局和局部搜索、控制参数少、易于实现、计算方便等。目前，人工蜂群算法的应用研究比较广泛，已经从最初的函数优化领域发展到训练神经网络、图像分割处理、路径优化、数据挖掘、组合优化、语音识别等领域。

但是，人工蜂群算法仍存在与其它群智能算法相同的问题，比如在搜索后期会出现收敛速度减慢、种群种类减少和全局搜索能力差等问题。为改善ABC算法的这些缺陷，众多研究人员进行了改进研究。Karaboga等[3]提出了改进的ABC算法（MABC），研究了控制参数变化频率的摄动率、缩放因子（步长）以及“limit ”对算法的影响，并用于解决实值参数优化问题；P.Guo等[4]受粒子群算法的启发，在搜索方程中引入全局最优和个体最优信息，使得算法在寻优过程中可以兼顾全局和局部最优解的引导，进而加快算法收敛速度和解的精确度；Banharnsakun等[5]提出利用当前全局最优解代替随机选取的邻域个体，根据当前全局最优解的适应度调整邻域搜索步长，从而改善算法解的精确度和收敛速度。除此之外，有的学者把混沌搜索引入到ABC算法中，比如：Alatas[6]提出了混沌人工蜂群算法，用于全局数值优化问题，算法中采用多种可选的混沌映射来改进算法的性能；暴励等[6]提出了自适应搜索空间的混沌蜂群算法，动态调整搜索空间的范围，达到加快解的收敛速度、避免最优解被排除在搜索空间外的效果；Gao等[8]提出一种改进ABC算法并将其用于混沌系统的控制和同步中，算法采用反向学习和混沌映射方法初始化种群，采用全局最优解引导进行邻域搜索过程，并通过实验证明了方法的可行性；罗钧等[9]提出了基于Logistic混沌搜索的蜂群优化算法，通过混沌映射进行初始化，以提高种群多样性，使算法可以在全局内进行搜索；张明等[10]提出基于适应值欧氏距离比的均衡蜂群算法，在初始化时引入混沌策略提高种群多样性；匡芳君等[11]提出了自适应Tent混沌搜索的ABC算法，该算法应用Tent映射得到算法的最初解，使得初始化个体尽可能均匀分布，再动态调整混沌搜索的空间大小，用目前的最优食物源得到Tent混沌序列，从而得到最优解等。有的学者利用熵来改进算法，熵是不确定性的一种度量，利用熵的值来度量算法中的不确定性，通过控制熵的值达到控制算法的目的。例如：李彦苍等[12]提出了基于信息熵的改进算法；徐双双等[13]提出基于平均熵的自适应ABC算法，利用平均熵机制初始化种群，增加种群的多样性，避免算法陷入局部最优等。

针对基本ABC算法收敛速度慢和搜索后期种群多样性降低的缺点，本文提出了一种改进的ABC算法，即在观察蜂阶段（onlooker bees）引入惯性权重，使用随着迭代次数动态变化的惯性权重因子来平衡种群的局部搜索和全局探测能力，防止算法陷入局部最优和加快寻优速度；在侦察蜂阶段（scout bees），利用正弦函数搜索操作，正弦函数服从均匀分布，能很好地搜索全部范围，以提高种群多样性。

2 基本人工蜂群算法

在ABC算法中，将蜜蜂分为三种类型: 雇佣蜂、观察蜂和侦察蜂。在搜索最优解的过程中，一个蜜源对应问题中的一个可行解，蜂群采蜜即搜索最优解的过程。可行解的质量问题由优化问题的适应度值决定，适应度值与可行解的质量成正比。

ABC算法的寻优过程主要由以下四部分组成:

2.1 雇佣蜂搜索

位置更新公式如下:

2.2 选择操作

ABC算法中，观察蜂通过“贪婪”选择策略对食物源进行选择，选择概率为:

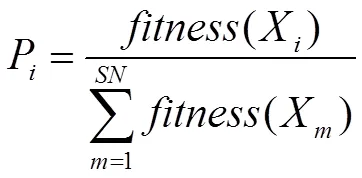
其中，考虑最小化问题：

（3）

2.3 观察蜂搜索

位置更新公式同式(1)。

2.4 侦察蜂搜索

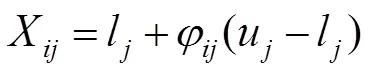
3 平衡蜂群算法

在基本ABC算法中，蜂群之间通过个体间进行共享信息来搜索新的食物源，具有很大的不确定性，可以基本搜索到所有解空间，所以，相对而言，基本人工蜂群算法具有较强的全局搜索能力，但其对当前找到的最优解并没有较强的局部搜索机制，开采与开发能力出现不平衡的状况，当算法搜索进行到后期时，种群多样性降低，搜索效率下降，从而使收敛速度减慢。本文采取两种方法来提高算法性能：在观察蜂阶段引入惯性权重，在侦察蜂阶段利用正弦函数搜索操作。

3.1 惯性权重因子

学者Shi等人在粒子群算法的速度公式中引入惯性权重，可达到提高收敛速度的效果[14]，惯性权重可达到保持粒子运动原状态的效果，进而可使搜索空间扩大，不至于陷入局部最优值。因为可达到平衡开采和开发能力的效果，所以通过的动态调整来改变开采和开发能力。在进行寻找最优解的过程中，比较好的选择是在搜索前期有较高的开发能力从而得到较好的解，而后要有较高的局部搜索能力以达到加快寻优的效果，因此，可将设定为递减变化。这样，在初始时可以实现广泛的搜索，而在算法后期将搜索空间的范围缩小，对找到局部最优有好处，可以使得算法性能更好。由此，本文设计了如公式( 5)所示的搜索方程，实现开发和开采的平衡。

（6）

3.2 正弦函数搜索

在算法搜索进行到后期，可能会引起种群的多样性降低，从而导致算法陷入局部最优，所以，需要采取一种提高全局搜索的方法，以提高种群多样性。已有文献指出sine（）服从均匀分布，可使解的分布尽可能均匀，全面覆盖搜索范围[15]，并已经成功应用到了DE算法中且取得了良好的结果。由此，本文设计了如公式 (7) 所示的正弦函数搜索公式，达到对解空间的全局搜索。

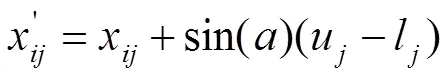
3.3 MABC算法流程

在改进的ABC算法（MABC）中，蜜蜂总数用NP表示，解的个数（SN）等于雇佣蜂的个数。一般,SN=NP/2。用表示第i个食物源（i=1,2,...,SN；D为搜索空间的维数)。

MABC算法的具体实现步骤如下：

步骤1）：随机产生NP个解，通过公式(4)随机产生可行解,记作。

步骤2）：对各个解的每一维的适应度函数值进行求解，按从大到小排序，取前SN个解作为最初的解，剩余的蜜蜂则为观察蜂。

步骤3）：对于每只雇佣蜂，在当前位置的邻域进行搜索新的位置，然后求出其适应度值，采用贪婪选择算法选择，取新位置和原位置中适应度值大的保存下来，搜索公式为公式(1)。

步骤4）：对于每只观察蜂，按照与食物源适应度值成比例的概率，选择一个食物源，并在其周围继续搜索，搜索其他蜜源，搜索公式采用经过改进后的公式(5)，若新产生的食物源适应度值比原食物源的大，那么观察蜂变为雇佣蜂，并更新食物源位置，反之，则保持原来的解不变。观察蜂通过概率选择公式(3)来选择。

步骤5）：当雇佣蜂的搜索次数到达一定阈值，limit却一直没有变化时，则要重新随机得到一个新的食物源位置，采用经改进后的公式(7)替代它。

步骤7）：判断是否满足停止准则：达到最大迭代次数maxCycle，若达到该条件，则停止计算并得到最优的食物源，若没有达到该条件，则算法要转向步骤 2）。

4 仿真实验与结果分析

4.1 Benchmark函数

为了测试改进人工蜂群算法（MABC）的性能，本文采用了5种经典的benchmark functions进行测试，如表1所示。其中，F01是单峰函数，主要用于测试算法是否具有寻优能力。F02是著名的经典优化问题，该函数是一个单峰函数，但是全局最优在一条长而窄的抛物线形的山谷中，难以收敛到全局最优值，并且各变量间有很强的关联性，梯度方向不指向最优值，所以常用来测试优化算法的性能。F03是球函数再加余弦模型，从而产生出许多局部极小，是多峰函数，找到全局最优值有一定的难度。F04是复杂的多峰函数，局部最优值的个数与维数成正比。F05 是多峰函数，用于测试算法的寻优能力。

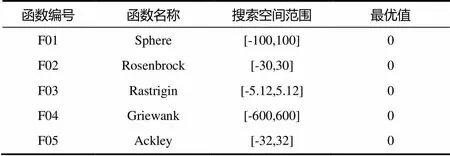
表1 实验中使用的Benchmark函数

4.2 与基本ABC算法的对比

将改进算法与基本ABC算法进行比较，2种算法采用相同的参数设置，以消除参数不同对算法的影响。实验中，食物源个数SN取30，最大搜索次数limit取100，最大迭代次数maxCycle取1000, 函数维度分别取D=30和D=50。算法执行结束后，记录结果的均值与标准差。测试结果如表2、表3所示，其中均值的作用是对算法寻优精度的体现，标准差的作用是算法稳定性的体现。

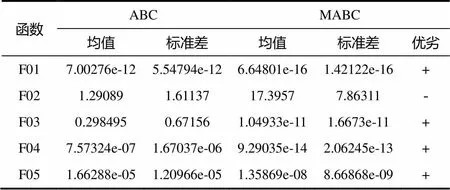
表2 D=30时基本ABC和MABC的实验结果

表3 D=50时基本ABC和MABC的实验结果

由表2可见，在单峰函数测试中，MABC算法在解的精度和稳定性两方面都优于基本ABC算法。在多峰函数的测试中, 除F02之外，MABC算法可以得到较高精度的解，并且性能均优于基本ABC算法。由表3可见，D=50时，MABC算法依然在大部分函数上要优于基本ABC算法。显而易见，寻优问题的难易程度与解的维数成正比，但MABC算法与基本ABC算法相比，寻优精度以及收敛速度都表现良好。为了更直观地反映MABC算法的收敛性能，图1～图4为两种算法对部分测试函数的收敛曲线，从总体来看，MABC算法的性能要优于基本ABC算法。

图1 Sphere函数进化曲线（D=30）

图2 Rastrigin函数进化曲线（D=30）

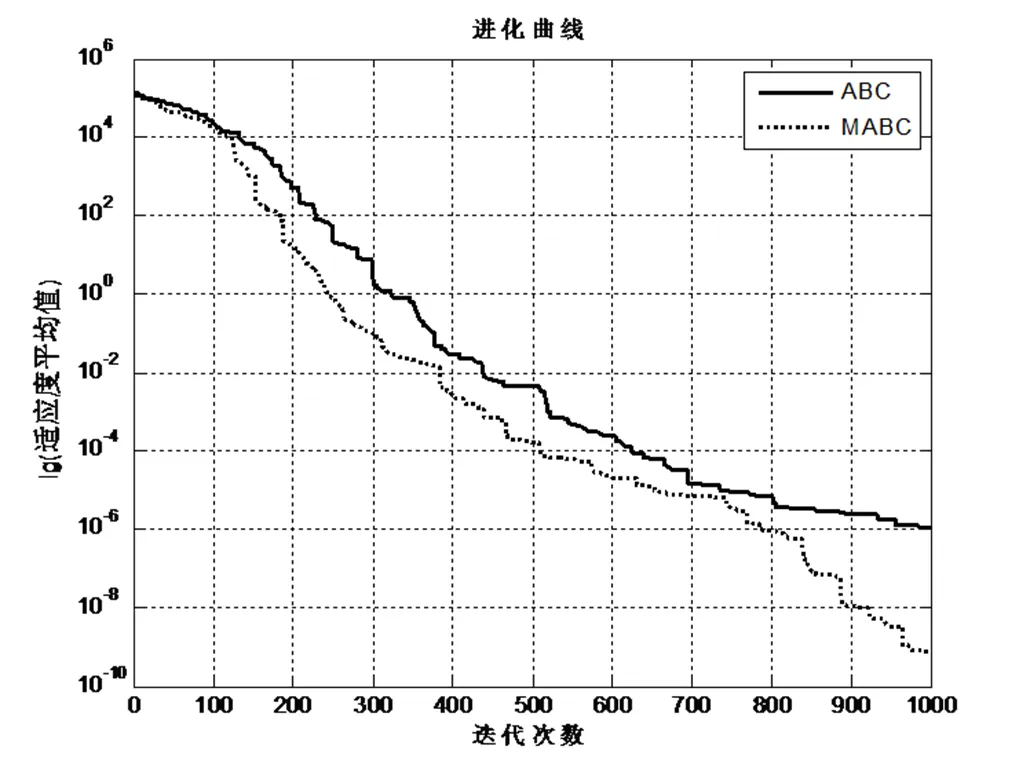
图3 Sphere函数进化曲线（D=50）

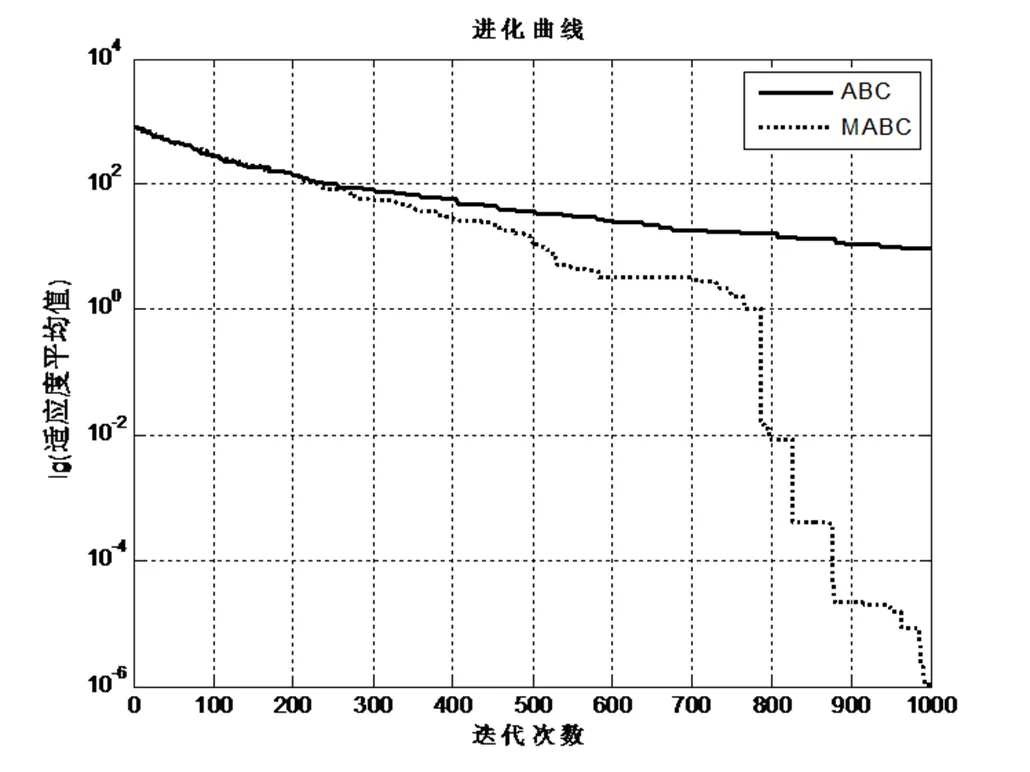
图4 Rastrigin函数进化曲线（D=50）

5 结束语

为了加快基本ABC算法的收敛速度并避免算法陷入局部最优，本文提出了改进的人工蜂群算法。算法在观察蜂阶段引入惯性权重，使用随着迭代次数动态变化的惯性权重因子来平衡种群的开发和开采能力，防止算法陷入局部最优和加快寻优速度；在侦察蜂阶段，利用正弦函数搜索操作，正弦函数服从均匀分布，能很好地搜索全部范围，以提高种群多样性。通过测试函数表明，该算法性能得到了改善。后续将把就该改进算法应用于实际工程中，以解决实际问题。

参考文献:

[1] Karaboga D, Basturk B. A powerful and efficient algorithm for numerical function optimization: artificial bee colony (ABC) algorithm[J]. Journal of Global Optimization, 2007, 39(3):459-471.

[2] Karaboga D, Basturk B. On the performance of artificial bee colony (ABC) algorithm[J]. Applied Soft Computing, 2008, 8(1):687-697.

[3] Akay B, Karaboga D. A modified Artificial Bee Colony algorithm for real-parameter optimization[J]. Information Sciences, 2012, 192(6):120-142.

[4] Zhu G, Kwong S. Gbest-guided artificial bee colony algorithm for numerical function optimization[J]. Applied Mathematics & Computation, 2010, 217(7):3166-3173.

[5] Banharnsakun A, Achalakul T, Sirinaovakul B. The best-so-far selection in Artificial Bee Colony algorithm[J]. Applied Soft Computing, 2011, 11(2):2888-2901.

[6] Alatas B. Chaotic bee colony algorithms for global numerical optimization[J]. Expert Systems with Applications, 2010, 37(8):5682-5687.

[7] 暴励, 曾建潮. 自适应搜索空间的混沌蜂群算法[J]. 计算机应用研究, 2010, 27(4):1330-1334.

[8] Gao W F, Liu S Y. A modified artificial bee colony algorithm[J]. Computers & Operations Research, 2012, 39(3):687-697.

[9] 罗钧, 李研. 具有混沌搜索策略的蜂群优化算法[J]. 控制与决策, 2010, 25(12):1913-1916.

[10] 张明, 田娜, 纪志成. 基于适应值欧式距离比的均衡蜂群算法[J]. 系统仿真学报, 2015, 27(5):980-989.

[11] 匡芳君, 徐蔚鸿, 金忠. 自适应Tent混沌搜索的人工蜂群算法[J]. 控制理论与应用, 2014, 31(11):1502-1509.

[12] 李彦苍, 彭扬. 基于信息熵的改进人工蜂群算法[J]. 控制与决策, 2015(6):1121-1125.

[13] 徐双双, 黄文明, 雷茜茜. 基于平均熵的自适应人工蜂群算法[J]. 计算机科学, 2015, 42(8):253-258.

[14] Shi Y, Eberhart R. Modified particle swarm optimizer[C]// IEEE International Conference on Evolutionary Computation Proceedings. IEEE World Congress on Computational Intelligence, 1998:69-73.

[15] 程正东, 章毓晋, 樊祥. 2DPCA在图像特征提取中优于PCA的判定条件[J]. 工程数学学报, 2009, 26(6):951-961.

华侨大学研究生科研创新能力培育计划资助项目。