适应性安全的可追踪叛徒的基于属性加密方案

马海英，曾国荪，陈建平，王金华，王占君



适应性安全的可追踪叛徒的基于属性加密方案

马海英1，曾国荪2，陈建平1，王金华3，王占君3

(1. 南通大学计算机科学与技术学院，江苏南通226019； 2. 同济大学计算机科学与技术系，上海201804；3. 南通大学理学院，江苏南通 226007)

针对基于属性加密(ABE, attribute-base encryption)机制存在的密钥滥用问题，为每个用户增加唯一的身份标识符，将联合安全编码和叛徒追踪机制引入到ABE方案中，给出适应性安全的可追踪叛徒ABE的定义、安全模型和可追踪模型，提出一种适应性安全的可追踪叛徒的ABTT方案，该方案允许适应性追踪指定策略盗版解码器中的叛徒。基于合数阶群上的子群判定假设和DDH假设，证明所提方案是适应性安全和适应性可追踪的。因此，所提方案不仅可以适应性追查指定策略盗版解码器中的叛徒，而且进一步增强了ABE系统的安全性，具有一定的理论和应用价值。

基于属性加密；叛徒追踪；双系统加密；适应性安全；联合安全编码

1 引言

基于属性加密(ABE, attribute-base encryption)机制作为一种新型的一对多的公钥加密机制，实现了对加密数据的细粒度访问控制[1,2]。然而，在ABE系统中，用户的访问权限与其私钥直接关联[3,4]。一个密文可以被满足访问策略的多个用户解密，如果合法用户泄露自己的私钥构造盗版解密设备，并将其分发给非法用户，则系统的访问控制策略将被打破[5,6]。特别的，用户私钥仅与其属性相关，不同用户可能会有相同属性，而与用户的任何特定信息(如身份)无关，即使盗版密钥被发现，也无法将其与任何合法用户相关联。因此，恶意用户可以轻易地与他人共享自己的私钥而不用担心被追究责任[5]，称这些恶意用户为叛徒。

针对基于属性加密中的密钥滥用问题，学者们进行了深入的研究，提出了不同的解决方案。2008年，Hinek等[3]提出一种基于标号的ABE方案。在该方案中，当用户需要解密密文时，利用在线的可信第三方，如果恶意用户拷贝或代理生成私钥，并分发给他人时，则将会导致该用户的个人隐私信息被泄露。该方案有效地抵制了ABE中密钥拷贝或密钥代理攻击，对预防密钥滥用起到威慑作用。但是，该方案不能追究密钥滥用者的责任。2009年，Yu等[7]和Li等[6]基于DBDH和D-Linear假设分别提出了防密钥滥用密钥策略ABE方案和可追责的匿名密文策略ABE方案，可追查到叛徒的真实身份，解决了ABE中叛徒非法行为的责任追究问题。2011年，Wang等[5]将联合安全编码[8]和叛徒追踪技术[9]引入到ABE机制中，提出了基于属性的叛徒追踪方案。然而，上述方案仅满足较弱的选择安全模型，即攻击者必须在生成系统公钥之前选择攻击目标。在实际应用的ABE系统中，系统公钥生成之后，攻击者可以适应性地选择攻击目标，构造盗版解码设备。因此，上述方案均不能满足实际密码系统对适应性安全的应用需求。同时，Wang等[5]将如何构建适应性安全的基于属性加密的叛徒追踪方案作为一个公开问题被提出。2013年，Liu等[10]提出了适应性安全的可追踪叛徒的密文策略ABE方案，将盗版解码器分为2种：1) 类密钥盗版解码器，显式地给出一个属性集，并将相应的私钥固化在盗版设备中，只要该属性集满足密文中访问策略，就能以不可忽略的概率解密密文；2) 指定策略盗版解密器，明确给出一个访问策略，该盗版解码器能以不可忽略的概率解密在该访问策略下加密的密文。该方案能够适应性追踪类密钥盗版解码器，但仅能选择性追踪指定策略盗版解密器。

为了构造出可适应性追踪指定策略盗版解密器中叛徒的ABE方案，本文需要解决以下2个问题。1) 由于在ABE机制中，可能存在多个用户具有相同属性集合，所以，ABE机制不能根据属性集合来严格区分用户。然而，叛徒追踪方案要求必须能够严格区分每一个用户。因此，每个用户除了拥有一个属性集合，还引入一个身份信息，即采用一对值(,)来标识每个用户。此外，为了使用户身份具有唯一性，本文利用联合安全编码[9]技术，将每个用户身份映射到一个码字。2) 授权中心根据用户的身份属性对(,)生成相应私钥，该私钥必定包含与身份对应的成分。为了保证本方案仍然是ABE方案，还需要解决另一个问题，即解密能否成功仅与用户拥有的属性集合相关，而与用户身份无关。本文在密文中引入一个向量，通过合理设计解密算法，使解密时能将密文和用户私钥中的身份信息相互抵销，不影响解密的前提条件。

本文通过修改Lewko等[11]提出的适应性安全的密文策略ABE方案，采用非对称的双线性对技术，将联合安全编码技术和Abdalla等[9]提出的叛徒追踪算法引入到该密文策略ABE方案中，提出一种适应性安全的可追踪叛徒的ABE方案。基于合数阶群上的子群判定假设和DDH假设，利用双系统加密技术[12]，通过一系列混合讨论，证明本方案是适应性安全和适应性追踪指定策略盗版解密器中的叛徒。因此，本方案不仅可以适应性追查叛徒，而且进一步增强了ABE系统的安全性，具有一定的理论和应用价值。

2 预备知识

2.1 联合安全编码

本节将简述联合安全编码的相关概念和结论，结合本文所提方案，采用文献[9]的符号来描述其定义。一个联合安全编码可以用(, N,)-联合安全码来表示，其中，表示叛徒追踪算法可允许的串谋用户的最大取值，N表示系统中用户的最大数目，表示追踪算法出错的概率值, 这样的一个联合安全码可以由长度为=(2(log(N)+log()))的码字和一个长度2的字母表来生成。

一个字母表为，长度为的联合安全编码由一个集合和一个追踪算法T组成。集合= {w(i)| 1 ≤≤N,Î{0,1}l}，记作编码本，其中，是长度为l的0和1的字符串，对1≤≤N,w(i)是索引的码字。对于最多为个串谋用户集合C⊆{1, ···, N}，= { w(i),ÎC }，和所有的多项式时间算法A，联合安全码满足Pr[T(,)ÎCÎ();A();{0,1}l]1。

这个概率值是由随机数、随机算法A和追踪算法T来决定的，A()表示当随机算法A在输入集合时，把输出结果赋值给；{0,1}l表示根据均匀分布选择的随机值Î{0,1}l。联合安全编码的详细资料可以参考文献[9]。

2.2 非对称合数阶双线性群和困难问题假设

下面给出非对称合数阶群上的困难问题假设，假设给定一个群生成器G，输入系统安全参数，输出非对称合数阶双线性群的描述(=123,1,2,G,)，其中，1,2,G均是阶为=123的循环群，双线性映射：1×2→G满足下列条件。1)双线性：1∈1,1∈2;,∈Z;(1­,1)(1,1)。2)非退化性：1∈1,1∈2使(1,1)在G中的阶为。3)可计算性：群1,2,G中的运算以及双线性映射都是在多项式时间内可计算的。4)正交性：令1, pi表示群1的p阶子群，2, pj表示群2的p阶子群(= 1, 2, 3;= 1, 2, 3)，如果1, p,2, p, 且时,(g, h) =1为G的单位元，则称其为群1和2上的正交性。令1,和2,分别表示群1和群2的pp阶子群，下面给出非对称合数阶群上子群判定困难问题假设。

2.3 访问结构和线性秘密共享方案(LSSS)

定义1 (访问结构[11])。假定P ={P1, P2, P3, ∙∙, P}是个参与者的集合，由P的某些非空子集构成的集族，称其为访问结构，其中，集族2，且是单调的，即对任意集合,，均有：如果且，那么。中的所有集合称为授权集，不在中的集合称为非授权集。

定义2 (LSSS[11])。在参与者集合P={P1, P2, …, P}上构造一个秘密共享方案Π是线性的，如果有：1)将Z上的一个向量构造成参与者的秘密分享值；2)对于这个秘密共享方案Π，存在一个1×2的秘密份额生成矩阵和行标号函数: {1, …,1}→P，假定∈Z是待共享的秘密值，随机选择2,3, …,r2∈Z，构成向量= (,2, …,r2)，设'为的转置，则'是1个秘密份额构成的向量，根据标号函数将秘密份额λ= ()(1≤≤1)分配给参与者()。

将LSSS引入到本文所提方案中，将属性作为参与者，则所有的授权属性集均包含在访问结构。

3 适应性安全ABTT定义和安全模型

本节描述适应性安全的可追踪叛徒的基于属性加密(ABTT, adaptively secure attribute-based encryption for traitor tracing)的形式化定义、安全模型和可追踪模型。在本方案中，每个用户使用一个对(,)来标识，其中，表示用户的身份，表示用户拥有的属性集合，且不同用户可以具有相同的属性集合。

3.1 适应性安全ABTT的定义

一个可追踪叛徒的基于属性加密方案形式上可以由以下5个概率多项式时间算法来构成。

1) 初始化算法。该算法输入安全参数和系统全部属性集合，输出系统公钥和主密钥。

2) 私钥生成算法。该算法输入主密钥和用户的身份属性对(,)，输出该用户的私钥K,ω。

3) 加密算法。该算法输入消息访问结构(,)和系统公钥，输出一个密文。

4) 解密算法。该算法输入一个密文、一个用户私钥K, ω和公钥，仅当私钥中的属性集合能够满足密文中的访问结构时，输出明文；否则，输出^表示解密失败。

5) 叛徒追踪算法。针对访问结构(,)的盗版解密设备，该算法拥有对该设备的访问权限，输出一组用户的身份，与这些身份对应的用户被认为是叛徒。

本方案的正确性可以描述为。系统运行初始化算法生成和，对于所有消息∈{0,1}*, 用户身份，当满足(,)时,Dec(KeyGen(,,), Enc(, (,),)) =的概率为1。

3.2 安全模型

本方案的适应性安全模型是通过挑战者S和攻击者A之间的交互性游戏来定义的。

1) 初始化：挑战者S运行本方案的初始化算法，并将生成的公钥发送给攻击者A。

step1 A适应性地询问用户(,)的私钥，挑战者生成私钥并其发送给A，A可以重复多次询问私钥。

2) 挑战阶段：A向挑战者S提交访问结构(,)、等长消息0和1，S抛掷一枚公平硬币∈ {0,1}, 计算= Enc(M, (,),)，并将发送给A。

step2 重复执行step1。

3) 猜测阶段：A输出对挑战密文的一个猜测值'∈ {0,1}。

若'=，且攻击者A在step1和step2中从未询问这类用户(,)的私钥，其中，满足挑战访问结构(,)，则称A赢得了这个游戏。攻击者A在上述游戏中获胜的优势定义为：AdvA=|Pr['=]−|。

定义3 如果任意多项式时间攻击者A赢得上述游戏的优势都是可以忽略的，则称这个可追踪叛徒的基于属性加密方案是适应性安全的。

3.3 可追踪模型

本节将构造出一种适应性安全的可追踪模型。在该模型下，攻击者可以自适应的选择挑战访问结构，且拥有一个针对该访问结构的盗版解密设备的访问权限。令,表示相关的2个安全参数，可追踪模型可以通过挑战者S和攻击者A之间的交互性游戏进行如下描述。

1) 初始化。挑战者S运行本方案的初始化算法，将生成的公钥发送给攻击者A。

2) 私钥生成询问。A可以多次询问属性身份对(ω, ID)的解密私钥，其中，下标表示第次询问。

3) 生成盗版解密设备。A构造一个针对挑战访问结构(,)的盗版解密设备，是一个概率电路的描述，当向输入随机密文时，输出消息。

令T表示攻击者A提交的私钥询问的用户身份集合，且要求在该集合中的任意身份ID对应的属性集合ω满足挑战访问结构(,)，如果同时满足如下3个条件，则说攻击者A在可追踪游戏中获胜。

2) Q =Æ或QËT。

3) 攻击者A提交的所有私钥生成询问中最多有个不同用户的身份，且与这些身份一起询问的属性集合满足挑战访问结构(,)。对于不满足挑战访问结构(,)的属性集合，攻击者的私钥生成询问次数不需要限制。

攻击者A在上述游戏中获胜的概率可定义为A打破本方案可追踪性的优势。如果任意多项式时间的攻击者A在上述追踪游戏中的优势是关于的可忽略函数，那么可追踪叛徒的基于属性加密方案是-TT-CPA安全的。

4 适应性安全ABTT方案

本方案采用非对称双线性对技术来构建，即：1×2→G, 存在一个可有效计算的同构映射：2→1，且要求该同构映射是不可逆的。本方案利用Z*中的部分元素来表示系统所有属性的集合，假定= {1,2, ···,N}表示所有用户的集合，表示符号字母表的大小，用长度为的字符串来表示一个码字，选择一个集合{1, 2, ···, N}上的随机置换。可信授权中心维持从用户ID到码字w(j)的映射，其中，是联合安全编码的随机串。对于非二进制的字母表，可以使用一个长度为=élbù的位串表示一个码字，Î{0,1}表示一个码字的位串编码，cw表示中的第位。选择一个长度为(+1)的向量= (0,1, ···,f)，其中，fÎ2, p1，令(f) =e，向量= (0,1, ···,e)是同构映射作用在向量上的映像。设f=(= 0,1, ···,), 则e=(f) =。利用向量和定义Waters散列函数[5,8]

其中，是满足cw=1的所有的集合。

Setup(,)→(,)该初始化算法根据系统安全参数生成阶=123的乘法循环群1、2和G,令1, p1和2, p1分别是群1和2的1阶子群，1,1,3分别是1, p1,2, p1,2, p3的生成元，且满足1=(1)。可信授权中心(TA)随机选择,ÎZ，对每个属性Î，随机选择sÎZ。此外，TA生成如上所述的2个向量和，选择秘密随机置换和用于联合安全编码的秘密值Î{0,1}l，将每个用户的映射到各自的码字，生成系统公钥和主密钥为

KeyGen(,,) →SK, ω假定用户拥有身份和属性集合，该私钥生成算法随机选择,'ÎZ，0,0',0"Î2, p3, 对每一个属性Î，随机选择RÎ2,p3, 令对应的码字为，计算用户私钥SK, ω为

Enc((,),,) →该加密算法利用访问结构(,)和公钥对消息进行加密，其中，是一个1×2的矩阵，是一个从的每一行到一个属性()的映射。该算法随机选择,2, …,vZ，组成随机向量= (,2, …,v2)。对矩阵的每个行向量，随机选择, 计算密文如下

Dec(,SK, ω,) →假定密文中的访问结构是(,)，仅当用户私钥SK, ω中的属性集合满足(,)时，该解密算法可以成功解密密文，否则，解密失败。解密密文需要执行如下过程，首先计算，其中，是使cw=1的所有的集合。然后，计算一组常量cÎZ，使得。计算

T((,),) →Q可信授权中心执行该叛徒追踪算法，该算法拥有一个对访问结构(,)的盗版解密设备的访问权限。令()表示关于的一个不可忽略函数，能以概率()成功解密在(,)下加密的密文。令表示4中的第(élbù(−1)+)个元素。对每一个1≤≤和1≤≤élbù，该算法初始化计数器ctr,j=0，执行次下面的测试过程。

1) 选择一个随机消息。

2) 用访问结构(,)加密消息，并生成一个密文((,),0,1,2,x,3,x,4,)

3) 从1中随机选择一个元素代替。

4) 使用替换后的密文访问。

5) 若D输出，则计数器的值ctr,j←ctr,j+1。

完成以上循环，位串'可以按如下规则重新构成，让',j表示'的第élbù(−1)+位，如果ctr,j≤4则',j=1，否则',j= 0。然后，把位串解码为长度是的符号串，最后利用联合安全编码的追踪算法计算QTC(,)，并输出叛徒的身份的集合。

上述方案的正确性计算过程如下

5 安全性和追踪性证明

为了证明本方案的安全性和追踪性，需要首先定义半功能密文和半功能私钥，然后将半功能私钥进一步分为1型半功能私钥和2型半功能私钥，但它们不会被应用在真实的系统中。为了构造半功能密文和半功能私钥，需要选择一些共用的参数2Î2, p2，2=(2)，对每个属性Î，随机选择zÎZ。对= 0, 1,…,, 随机选择δÎZ。

半功能密文：半功能密文算法首先利用加密算法生成正常密文((,),0,1,2,x,3,x,4,")，选择随机值ÎZ和随机向量Î，对访问矩阵的每一行，随机选择γÎZ, 计算半功能密文如下

1型半功能私钥：该算法随机选择,,,'ÎZ,0,0',0'',RÎ2, p3，计算1型半功能私钥为

2型半功能私钥：该算法随机选择,,'ÎZ,0,0',0'',RÎ2, p3，选择子群2, p2的生成元2，计算2型半功能私钥为

值得注意的是，2型半功能私钥相当于将1型半功能私钥的指数= 0。当使用半功能私钥解密半功能密文时，得到多余项为，其中，1是向量的第一个分量，即<1, 0,…, 0>。此时，半功能密文和1型半功能私钥中的z是相同的，当用半功能私钥解密半功能密文时，这些z值将会被消掉，从而不影响解密。相反地，这些z是用来隐藏半功能密文在子群1, p2中被共享1的值。这里要求访问结构中的每个属性只能使用一次，当攻击者有一个不能解密挑战密文的1型半功能私钥时，根据信息理论可知，它能获知关于z的信息是可忽略的。如果在访问结构中每个属性可以多次使用，则z的值将会多次暴露给攻击者。在下列定义的每个游戏中，1型半功能私钥至多出现一次，其他半功能私钥都是2型的，这样就可以避免多次泄露z的值。

如果−1=0，则称该1型半功能私钥是名义半功能私钥，即名义半功能私钥可以成功解密相应的半功能密文。

5.1 安全性分析

本文所提方案是通过修改文献[11]的密文策略ABE方案而构造的，本文方案的安全性证明过程与这个密文策略ABE方案类似，基于假设1～假设3，可以证明本文方案是适应性安全的。由于篇幅有限，本文不做详细说明，其具体安全性证明过程可以参考文献[11]。

5.2 可追踪性证明

基于子群1,1上的DDH假设和合数阶群2上的静态假设1、2、4、5，利用混合争论技术，借助一系列相邻游戏(TraceReal, Trace0, Trace1,1, Trace1,2,…, Trace−1,2, Trace,1, Trace,2,…, Trace−1,2, Trace,1, Trace,2)的不可区分性，证明本文方案的可追踪性，其中，是攻击者询问私钥的最大次数。

TraceReal：一个真实的本方案的可追踪性游戏，私钥和密文都是正常的。

Trace0：与TraceReal类似，除了挑战者S生成半功能密文发送给盗版解码器。

Trace,1：与Trace0类似，除了前−1次询问的私钥是2型半功能的，第次询问私钥是1型半功能的，剩余的私钥是正常的。

Trace,2：与Trace0类似，除了前次询问的私钥是2型半功能的，剩余的私钥是正常的。

Trace,2：在这个可追踪性游戏中，所有询问私钥都是2型半功能的，且挑战者S生成半功能密文发送给盗版解码器。

定理1 如果所有串谋者C的码字中cw′, j′= 0，那么成功解密一个(′,′)位置被篡改的密文的优势为0，有

其中，S1是一个依赖于攻击者A的概率多项式时间算法。

算法S1接收到DDH假设的输入(1,1,)，令′=élb2ù(′−1) + (−1)。S随机选择,ÎZ，对每个属性Î，随机选择sÎZ。此外，对= 0, 1, ···,且≠时，随机选择θÎZ，计算e=, f=；当=时，令e=1,f=^。S1选择秘密随机置换和用于联合安全编码的秘密值Î{0,1}l，将每个用户的映射到各自的码字，生成系统公钥和主密钥为

当A提交身份和属性集合时，S1随机选择,'ÎZ，0,0',0"Î2, p3, 对每一个属性Î，随机选择RÎ2,p3, 令对应的码字为，计算用户私钥SK, ω为

注意：由条件cw= 0，可知()与f无关，所以S1在不知道f的情况下仍然可以计算该用户的私钥。然后，攻击者A构造出一个针对挑战访问结构(,)的盗版解密设备。

S1产生一个随机消息，随机选择2′, …,v2′Z，组成随机向量′= (1,2′, …,v2′)，对访问矩阵的每个行向量，随机选择, 计算密文如下

如果=1，那么该密文是正确生成的随机密文，此时，正确解密密文的概率为()。如果是随机的，该密文是4中的第′位被篡改的密文，那么正确解密篡改密文的概率为()−。所以算法S1以

的优势解决1,p1中的DDH假设。

引理1 当所有串谋者C的码字中cw, j'=1时，如果存在一个概率多项式时间攻击者A使TraceRealAdvA– Trace0AdvA=，那么可以构造一个概率多项式时间挑战者S，以的优势攻破假设1。

证明 挑战者S接收到假设1的条件{1,3,}，能够模拟TraceReal或Trace0。S随机选择,ÎZ，对每个属性Î，随机选择sÎZ。此外，对= 0, 1, ···,, 随机选择θÎZ，计算1=(1), 向量= ()=0,1,···,,向量=()=0,1,···,,选择秘密随机置换和用于联合安全编码的秘密值Î{0,1}l，将每个用户的映射到各自的码字，生成系统公钥和主密钥为

当A询问私钥时，S利用和密钥生成算法给A颁发正规私钥。然后，攻击者A构造出一个针对挑战访问结构(,)的盗版解密设备。

S产生一个随机消息，随机选择2′, …,v2′Z，组成随机向量′= (1,2′, …,v2′)，对访问矩阵的每个行向量，随机选择r′Z, 利用挑战访问结构(A,)计算第位被篡改的密文如下。

其中，上述密文隐式的设置=(,2, ···,),r=sr,是随机向量，其第一个分量为，且r是随机值。当Î2,1时，，该密文是第′位被篡改的正规密文。当Î2,12时，令=, 此时，该密文是半功能密文，其中，=，γ=−cr，z(x)=s(x),,δ=θ。尽管半功能密文中重复使用了2,1部分的值，但是，由中国剩余定理可知，, r',2', ···,, s(x),θmod1与, r',2', ···,, s(x),θmod2是无关的，上述密文是第′位被篡改的半功能密文。因此，S可以根据A的输出，以优势攻破假设1。

引理2 当所有串谋者C的码字中cw', j'=1时，如果存在一个概率多项式时间攻击者A使Trace1,2AdvA–Trace,1AdvA=，那么可以构造一个概率多项式时间挑战者S，以几乎为的优势攻破假设2。

证明 挑战者S接收到假设2的条件{1,12,3,23,}，能够模拟Trace−1,2或Trace,1。S随机选择,ÎZ，对每个属性Î，随机选择sÎZ。此外，对= 0, 1, ···,, 随机选择θÎZ，计算1=(1), 向量= ()=0,1,···,,向量=()=0,1,···,，选择秘密随机置换和用于联合安全编码的秘密值Î{0,1}l，将每个用户的映射到各自的码字，生成系统公钥和主密钥为

下面将A的私钥询问分为以下3种情况：1)当A询问私钥次数大于时，S利用和私钥生成算法给A颁发相应正规私钥；2)当A询问私钥次数小于时，S随机选择,'ÎZ,0,0',0'',RÎ2, p3，计算2型半功能私钥为

其中，2,3和1的值是不相关的，因此，该私钥是一个均匀分布的2型半功能私钥；3)当A进行第次私钥询问时，令的G1部分为1，S随机选择'ÎZ,0,0',0'',RÎ2, p3，计算

S产生一个随机消息，隐式地设置1=，2=，随机选择r',2,…, u2ÎZ, 生成向量'=(1,2,…, u2), 用挑战访问结构(,)对消息进行加密，计算第′位被篡改的密文

其中，上述密文隐式地设置=−1,=, 因此，是1,1部分被分享的值，是1,2部分被分享的值，且r=sr',γ= −cr'，z(x)=s(x),此时，当第个私钥是1型半功能时，z(x)在半功能密文和密钥中是一致的，δ=θ。

当第个私钥是1型半功能时，1与mod2相关，密文中的第一个分量为，−1=–= 0 mod2，此时该1型半功能私钥是名义半功能私钥。因此，第个私钥可能是名义半功能的或正规的。

为了证明挑战密文1,2中被分享的值1=在信息理论上是隐藏的，需要限制访问结构(,)中每个属性在中至多出现一次。因为第个私钥无法解密挑战密文，所以中()的所有行生成的行空间不包含1。因此，存在一个向量使正交于，但不正交于1，即1·≠0。固定一个包含的基，则存在, 使=+'' mod2，其中，''属于除外的基向量扩张的空间中，注意到''是均匀分布的，且无法揭露的任何信息。由于·1=·1·+1·''，且1·≠0，所以''·1与相关。

由于仅出现在+γz(x)中，当()时，=A·(·+'')=·u''，与无关。当()时，若γ≠0 mod2，每项''+γz(x)都引入一个新的未知量z(x)，且z(x)不出现在其他项中，因此，A无法从这些项中得知的任何信息。准确的说，无论的第一个分量为何值，上述方程都有相同个数的解，因此，当所有的γmod2都不为0时，在A看来，挑战密文和第个私钥以几乎为1的概率均匀分布。

引理3 当所有串谋者C的码字中cw', j'= 1时，如果存在一个概率多项式时间攻击者A使Trace,1AdvA–Trace,2AdvA=，那么可以构造一个概率多项式时间挑战者S，以几乎为优势攻破假设2。

证明 挑战者S接收到假设2的条件{1,12,3,23,}，能够模拟Trace,1或Trace,2。S随机选择,ÎZ，对每个属性Î，随机选择sÎZ。此外，对= 0, 1, …,, 随机选择θÎZ，计算1=(1), 向量= ()=0,1,···,,向量= ()=0,1,···,, 选择秘密随机置换和用于联合安全编码的秘密值Î{0,1}l，将每个用户的映射到各自的码字，生成系统公钥和主密钥为

下面将A的私钥询问分为以下3种情况。1)当A询问私钥次数大于时，S利用和私钥生成算法给A颁发相应的正规私钥。2)当A询问私钥次数小于时，2型半功能私钥与引理2的构造方法相同。3) 当A进行第次私钥询问时，与引理2的构造方式类似，但需要增加一个随机值Î，计算

唯一不同的是，1中增加了一项(23)，该项重新随机化了1的2,2部分。然后，攻击者A构造出一个针对挑战访问结构(,)的盗版解密设备。第′位被篡改的密文的构造方式与引理2相同，注意此时，第次私钥不再是名义半功能的。如果用第次私钥解密挑战密文，−1≠ 0，解密将会失败。

引理4 当所有串谋者C的码字中cw, j'= 1时，如果存在一个概率多项式时间攻击者A使Trace,2AdvA=，那么可以构造一个概率多项式时间算法S，以的优势攻破假设4。

证明 挑战者S接收到假设4的条件{1,,3,,2}，能够攻破Trace,2。S随机选择ÎZ，计算，对每个属性Î，随机选择sÎZ，计算。此外，对= 0, 1,···,, 随机选择θÎZ，计算1=(1)，向量= ()=0,1,···,,向量= ()=0,1,···,, 选择秘密随机置换和用于联合安全编码的秘密值Î{0,1}l，将每个用户的映射到各自的码字，生成系统公钥

为了生成2型半功能私钥，S随机选择,'ÎZ,0,0',0'',RÎ2, p3，计算

然后，攻击者A构造出一个针对挑战访问结构(,)的盗版解密设备。

S产生一个随机消息，隐式的设置指数来自于项，随机选择值r',2,…, u2ÎZ, 生成向量'=(,2,…, u2),用挑战访问结构(,)对消息进行加密，计算第′位被篡改的密文

其中，上述密文隐式设置=−1',='，因此，是1,1部分被分享的值，是1,2部分被分享的值，且r=sr',γ=−cr'，z(x)=s(x), δ=θ。

如果盗版解密设备成功解密上述密文的概率为2，则算法S可以以相同的概率计算出=(1,1)作为假设4的解，所以1≤Adv4G,A()是可以忽略的。

定理2 如果所有串谋者C的码字中cw', j'= 1，那么成功解密一个(',')位置被篡改密文的优势2是可忽略的。

证明 如果假设1、2、4、5成立，根据引理1~引理4可知，追踪性游戏TraceReal和Trace,2是不可区分的，由于在Trace,2中攻击者A成功解密一个(,)位置被篡改密文的优势是可忽略的，所以，在TraceReal中成功解密一个(,)位置被篡改密文的优势2是可忽略的。

定理3 本文适应性安全的ABTT方案满足-TT-CPA可追踪性，如果下面3个条件同时成立：1)本文方案采用的编码是字母表长度为、字符串长度为的(,,)联合安全编码；2)假设在1,1上成立；3)假设1~假设4在2上成立。即任意概率多项式时间的攻击者A生成一个不可追踪的盗版解密设备的优势。≤élbù(2e−λ)。其中，至多利用个串谋者的私钥以()的概率成功解密密文，且

证明 假定A是本方案可追踪性的攻击算法，输入系统公钥，输出一个盗版解密设备。利用A构造针对联合安全编码的攻击算法A′，输入个随机代码字= {1,…,cw}，输出一个字符串。下面证明，如果A能够以不可忽略的概率避免被追踪，那么A′能以不可忽略的概率输出一个不能被追踪的代码字。

A′随机选择1,…,iÎ{1,…,N}，设置串谋集合C= {1,…,i}，输入对应的码字

= {,=1, 2,…,}

A′运行本方案的初始化算法，生成系统公钥

A至多进行次私钥生成询问，设A第次进行私钥询问时的输入为(,)，A′用为其生成相应的私钥。因为包含随机串谋集C的代码字，因此是一个随机置换，所以，A′返回给A的私钥是均匀分布的。然后，A构造出一个针对挑战访问结构(,)的盗版解密设备。A′运行本方案的追踪算法，输出字符串，根据定理1、定理2和文献[8]中的Chernoff界，可知追踪算法输出的字符串不属于可行集()的概率，至多为Pr[Ï()]≤élbù(2e)。由(,,)联合安全编码的性质可知，定理3成立。

5.3 仿真实验的结果分析

为了验证本方案能够适应性追踪叛徒，基于双线性对程序库PBCL，通过适当修改libfenc程序库[13]中密文策略ABE的部分代码，实现了本方案，并对其进行仿真实验。假定系统安全参数=159，最多串谋叛徒个数=2，用户总数为1 024，追踪算法出错概率为10−6，则可以将联合安全码字长度取值为60位。一个具体的联合安全编码的构建是比较复杂的，由于篇幅有限，下面简单介绍联合安全编码工作原理，重点介绍本文叛徒追踪算法的实验结果。在本文方案中，有1 024个码字1,2, …,1024，并将其分配给所有用户。利用这些码字，任何2个用户均可定义一个可行集合，分别记为FS1,2, FS1,3, …, FS1 023,1 024，此处FS,j表示由码字w和w定义的可行集合。令该实验中，2个串谋用户的码字为1和2，他们的可行集合为FS1,2。根据本文叛徒追踪算法，对码字二进制串的每位运行404 496次测试，经过大量实验可得如下结果：1) 当所有叛徒位串的第(,)位cw,j都是1时，从1中随机选择一个元素代替密文4中的第(élbù(−1)+)个元素，此时解密成功的次数ctr为0次或1次，远远小于4=636次，由追踪算法可知，其重构位的值是1；2) 当所有叛徒位串的第(,)位cw,j都是0时，从1中随机选择一个元素代替密文4中的第(élbù(−1)+)个元素，此时解密成功的次数ctr为2 543次，远远大于636次，由追踪算法可知，其重构位的值是0；3) 当所有叛徒位串的第(,)位cw,j不相同时，修改密文中相应位置的元素为随机值时，解密成功的次数将在0~2 544次随机取值，由追踪算法可知，该位可能被重构为0或1，但这些位不影响叛徒码字的可行集合。由上述3种情况可以构造出叛徒码字的可行集FS12，利用联合安全编码的追踪算法，可追踪到叛徒的一组身份。总之，本文的追踪算法能够成功追查叛徒。

5.4 性能比较

表1列出本文ABTT方案和相关方案在效率和追踪性方面的详细比较，其中，1表示密文中访问矩阵的行数，||表示集合中属性的个数，||表示解密钥中满足访问策略的属性个数，N表示系统中用户的最大数目，表示联合安全编码中一个码字的二进制位数。

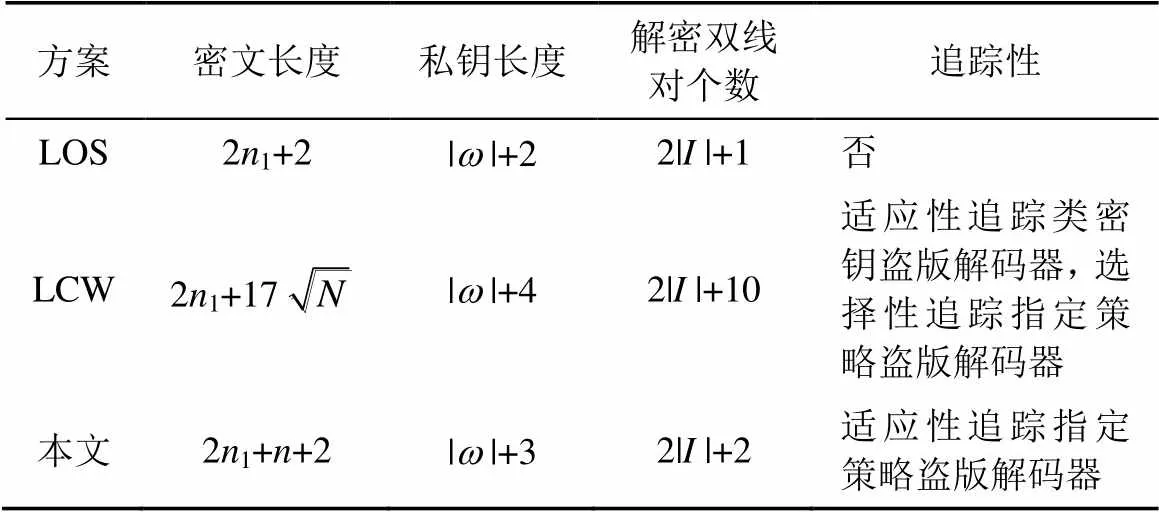
表1 本文ABTT方案与相关方案的性能比较

与文献[11]的LOS方案相比，虽然密文长度增加了个群中的元素，但本方案实现了适应性叛徒追踪的功能。与文献[10]的LCW方案相比，尽管本方案只能容忍指定个数叛徒构造盗版解码器，但是实现了指定策略盗版解密器的适应性追踪。

6 结束语

为了增加可追踪叛徒的基于属性加密机制的安全性，本文修改了适应性安全的密文策略ABE方案[11]，将叛徒追踪机制和联合安全编码引入到该方案中，给出了适应性安全的ABTT的定义、安全模型和追踪模型，提出了一个适应性安全的ABTT方案。基于合数阶群上的静态假设和DDH假设，证明本方案是适应性安全和适应性可追踪的。因此，该方案不仅可以适应性追查指定策略盗版解码器中的叛徒，而且进一步增强了ABE系统的安全性，具有一定的理论和实用价值。

[1] SAHAI A, WATERS B. Fuzzy identity based encryption[C]//The EUROCRYPT. Aarhus, Denmark, c2005: 457-473.

[2] GOYAL V, PANDEY O, SAHAI A, et al. Attribute-based encryption for fine-grained access control of encrypted data[C]//The 13th ACM Conference on Computer and Communication Security. Alexandria, Virginia, USA, c2006: 89-98.

[3] HINEK M J, JIANG S, SAFAVI-NAINI R, et al. Attribute-based encryption with key cloning protection[EB/OL]. http://eprint.iacr.org/ 2008/478.pdf.

[4] 马海英, 曾国荪. 可追踪并撤销叛徒的属性基加密方案[J]. 计算机学报, 2012, 35(9):1845-1855.

MA H Y, ZENG G S. An attribute-based encryption scheme for traitor tracing and revocation together[J]. Chinese Journal of Computers, 2012, 35(9):1845-1855.

[5] WANG Y T, CHEN K F, CHEN J H. Attribute-based traitor tracing[J]. Journal of Information Science and Engineering, 2011, 27(1):181-195.

[6] LI J, REN K, KIM K. A2BE: accountable attribute-based encryption for abuse free access control[EB/OL]. http://eprint.iacr.org/2009/ 118.pdf.

[7] YU S C, REN K, LOU W J, et al. Defending against key abuse attacks in KP-ABE enabled broadcast system[C]//The Security and Privacy in Communication Networks. Athens, Greece, c2009: 311-329.

[8] BONEH D, SHAW J. Collusion-secure fingerprinting for digital data[C]//The CRYPTO’95. Santa Barbara, California, USA, c1995: 452-465.

[9] ABDALLA M, DENT A W, MALONE-LEE J, et al. Identity-based traitor tracing[C]//The public Key Cryptography. Beijing, China, c2007: 298-314.

[10] LIU Z, CAO Z, WONG D S. Blackbox traceable CP-ABE: how to catch people leaking their keys by selling decryption devices on eBay[C]//The 20th Conference on Computer and Communication Security. Berlin, Germany, c2013: 475-486.

[11] LEWKO A, OKAMOTO T, SAHAI A, et al. Fully secure functional encryption: attribute-based encryption and (hierarchical) inner product encryption[C]//The EUROCRYPT. c2010: 62-91.

[12] WATERS B. Dual system encryption: realizing fully secure ibe and hibe under simple assumptions[C]//TheCRYPTO’09. Santa Barbara, California, USA, c2009:619-636.

[13] GREEN M, AKINYELE A, RUSHANAN M. Libfenc: The Functional Encryption Library[EB/OL]. http://code.google.com/p/libfenc.

Adaptively secure attribute-based encryption for traitor tracing

MA Hai-ying1, ZENG Guo-sun2, CHEN Jian-ping1, WANG Jin-hua3, WANG Zhan-jun3

(1. College of Computer Science and Technology, Nantong University, Nantong 226019, China; 2. Department of Computer Science and Technology, Tongji University, Shanghai 201804, China; 3. School of Science, Nantong University, Nantong 226007, China)

For the key abuse problem in attribute-based encryption (ABE), each user was identified by his unique identity, and the collusion secure codes and the traitor tracing mechanism were introduced to the ABE scheme. The definition, security model and tracing model for adaptively secure attribute-based encryption for traitor tracing (ABTT)were formalized, and an adaptively secure ABTT scheme was proposed, which may trace traitors in policy-specific pirate decorders. Under these subgroup decision assumptions in composite order groups and the DDH assumption, adaptively secure and can adaptively trace traitors were proved. Therefore, the scheme not only was capable of tracing adaptively traitors in policy-specific pirate decorders, but also further strengthens the security of ABE system, which has theoretical and practical values.

attribute-based encryption, traitor tracing, dual system encryption, adaptive security, collusion secure code

TP309

A

10.11959/j.issn.1000-436x.2016009

2014-12-20；

2015-03-19

国家自然科学基金资助项目(No.61402244, No.61272424, No.61202006, No.61272107, No.61202173, No.61103068)；NSFC-微软亚洲研究院联合基金资助项目(No.60970155)；上海市优秀学科带头人计划基金资助项目(No.10XD1404400)；教育部博士点基金资助项目(No.20090072110035)；上海自然科学基金资助项目(No.13ZR1443100)；南通大学校级自然科学基金资助项目(No.15Z06)

The National Natural Science Foundation of China (No.61402244, No.61272424, No.61202006, No.61272107, No.61202173, No.61103068), The Joint of NSFC and Microsoft Asia Research (No.60970155), The Program of Shanghai Subject Chief Scientist(No.10XD1404400), The Ph.D Programs Foundation of Ministry of Education China(No.20090072110035), ShanghaiNaturalScienceFoundationProgram(No.13ZR1443100), TheNatural Science Foundation of Nan tong University(No.15Z06)

马海英（1977-），女，河南卫辉人，博士，南通大学副教授，主要研究方向为公钥密码学和网络安全。

曾国荪（1964-），男，江西吉安人，同济大学教授、博士生导师，主要研究方向为网格计算、可信软件。

陈建平（1960-），男，江苏南通人，南通大学教授、硕士生导师，主要研究方向为信息安全、数值计算等。

王金华（1963-），男，江苏南通人，博士，南通大学教授、博士生导师，主要研究方向为信息安全、组合数学等。

王占君（1978-），男，河南鹤壁人，南通大学讲师，主要研究方向为公钥密码学和Hopf代数。