电磁脉冲探头校准系统

刘星汛，韩玉峰，张 涛



电磁脉冲探头校准系统

刘星汛1, 2，韩玉峰2，张 涛1

(1. 天津大学电气与自动化工程学院，天津 300072；2. 北京无线电计量测试研究所，北京 100058)

面向电磁脉冲探头准确计量的需求，设计了一套基于标准场法的电磁脉冲探头校准系统，从时域激励信号的傅氏分析出发，分析了系统的频域特性，通过仿真实验确定了场强幅度均匀的校准区，研究了电磁脉冲探头硬件积分和软件积分校准方法，并采用此校准系统分别对D-dot探头和光电探头进行重复性和线性度实验，实验结果表明校准系统重复性优于2.8%,，能够有效地解决电磁脉冲探头量值溯源问题．

电磁脉冲；探头；校准

电磁脉冲信号由于高强度、大功率、强大破坏作用等优势，常常被用于现代化信息战争．为提高武器系统的作战性能，美国早在1986年就将瞬变电磁场辐射敏感度的测试方法(RS05，在后来的版本中代号改为RS105)列于军用电磁兼容(EMC)标准[1]中，并根据标准对其战略核导弹进行了抗核电磁脉冲(NEMP)加固设计、加固工程以及验证测试．随着国防技术的发展，电磁脉冲信号运用越来越广泛，不管是加固设计还是验证实验，均离不开测量探头对电磁脉冲场强的测量，而探头的精确校准决定了场强测量的准确性．

目前测量电磁脉冲场强的探头通常分为两大类：一类是D探头，美国人最早从源区电磁脉冲测量的需要而研制的，探头测量的微分信号通过积分变换得到电磁场强度，比如瑞士Montena公司的D-dot探 头[2]，中国工程物理研究院卫兵等[3-4]利用阳加速器自行设计的D探头等均属于此类探头；另一类是光电探头，利用光调制测量电磁场的传感器，如陈福深 等[5-6]研究的光波导探测器，曾嵘等[7]研究的光电测试系统．采用探头测量电磁脉冲场强时，由于缺乏探头校准的手段，使得场强测量值只有参考价值，而不能用于实验或加固设计对电磁场定量的判断．为了准确测量脉冲场，国外专家很早就研究了电磁脉冲探头的校准方法[8]，国内近年来才开始这方面的研究，石立华等[9]针对脉冲磁场测量的要求，组建了时域标定系统，对传感器的时域校准进行了研究，陈竞等[10]介绍了一种动态范围为0.1～25,kV/m的电磁脉冲场产生装置，并通过光纤传输对脉冲传感器的灵敏度、响应特性进行了实验，谢彦召等[11]也进行了相关研究，然而这些研究主要针对探头测量结果定性的分析，并没有对校准系统的标准场进行定量的研究．因此，本文从采用标准场法校准脉冲探头出发，建立电磁脉冲探头校准系统，分析了系统的频响特性，分别从仿真和实验两方面，对探头校准系统性能进行了验证．

1 电磁脉冲探头校准系统

与场强探头校准方法类似，电磁脉冲探头的校准也可采用标准场法，信号源将时域脉冲信号注入到TEM小室中，并形成一个可计算的场强，将探头测量的场强值与理论值比较，校准出探头的修正系数．

1.1 RS105探头校准系统

电磁脉冲探头时域校准系统如图1所示，由EMP信号源、TEM室、衰减器、示波器等部分组成．脉冲信号发生器向TEM室注入一高压电磁脉冲信号，在小室中产生一标准场，其峰值场强为，待测探头放在小室的中央，双通道示波器的通道1通过衰减器连接小室的输出端口，通道2连接待测探头. 为了满足阻抗匹配，减少能量反射，示波器通道1的输入阻抗与TEM室的特性阻抗相同设为50,W，示波器通道2阻抗应与电磁脉冲探头的输出阻抗一致.

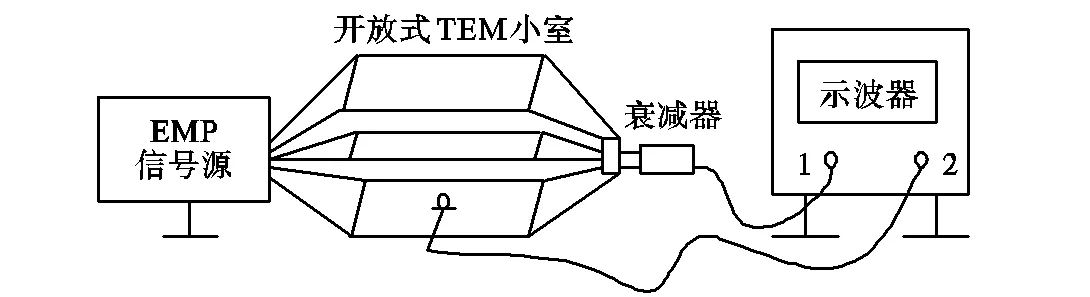
图1 电磁脉冲探头时域校准系统

被校探头修正系数计算式为

   (1)

式中：为探头修正系数，kV/(m·mV-1)；为TEM室中的标准场强，kV/m；为探头测量的峰值电压，mV；1为示波器通道1所监测信号的峰值电压，mV；为TEM室高度，m；为TEM室输出端口与示波器之间连接的衰减器系数，dB．

1.2 激励信号的傅氏分析

信号源注入的激励信号如图2(a)所示，上升时间为1.8,ns，脉宽34.2,ns，下降时间为2.4,ns，由于时域激励信号包含了丰富的频谱信息，脉冲信号的上升时间决定了校准频率的分布带宽，上升时间越短，信号的频域带宽就越宽．而校准用的开放式TEM室工作截止频率为500,MHz，为了判断输入信号的各频谱分量是否均能在TEM室里进行传输，因此将注入电磁脉冲信号进行离散傅里叶变换．

取激励信号的时间步进为0.05,ns，经过2,000个点的离散傅里叶变换后的归一化频谱如图2(b)所示，激励信号包含了丰富的频谱，其信号包络一直到1,GHz以上，但是主要能量集中在200,MHz以下，到500,MHz以后的频谱分量的能量很小，占总能量的1%,以下，截止频率为500,MHz的TEM室能满足校准需要，500,MHz以上的频谱分量的截断不会影响校准结果．

（a）校准的激励时域波形

（b）激励波形归一化频谱

图2 激励信号的傅氏分析

Fig.2 Fourier transform of exciting signal

2 仿真实验

探头校准应确定校准区，为了保证探头校准的精度，应保证校准区中场强均匀且探头尺寸对场的扰动较小，对于时域脉冲信号应确保区域内各点的电磁脉冲场峰值电压相当，根据标准IEEE1309—2005的规定[12]，针对连续波场强标准，假设TEM室空间尺寸为××，当探头尺寸小于，如图3所示，探头对场的影响小于10%,，标准场法探头校准结果影响小于1%,．假定校准区为，通过仿真判断校准区内脉冲场均匀性．

（a）侧面图

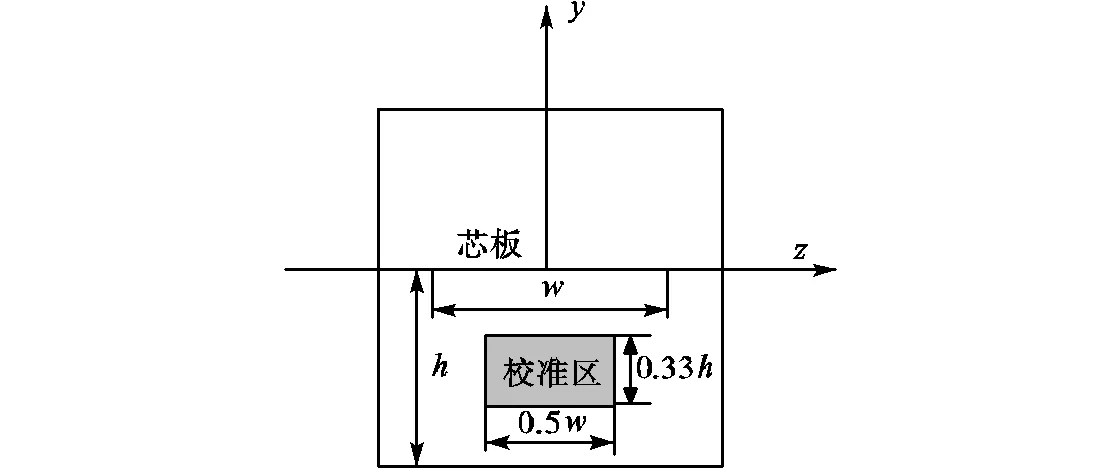
（b）主视图

图3 TEM室结构尺寸示意

Fig.3 Physical dimension of TEM cell

从TEM室注入能量为1,W的归一化时域脉冲信号，4,ns后沿传播方向的场强分布如图4所示，TEM室各固定位置点的场强结果如表1所示，相同值所对应的平面的各点峰值场强幅值相差较小，最大仅为1.1,V/m，在方向，靠近外壳底板的部位场强较小，为了得到在方向详细的场强分布信息，在平面分别过(0，0)、(120 mm，－144 mm)2个点，画平行于轴的直线，线上的场强分布曲线如图5所示，这2条线上的场强分布呈现相同的趋势，芯板内部场强为0，芯板与底板之间场强基本均匀，但是由于边缘效应的影响，距离外壳底板较近场强幅度随位置变化而变化剧烈，因此校准区尽可能选在场强均匀的中心位置处．

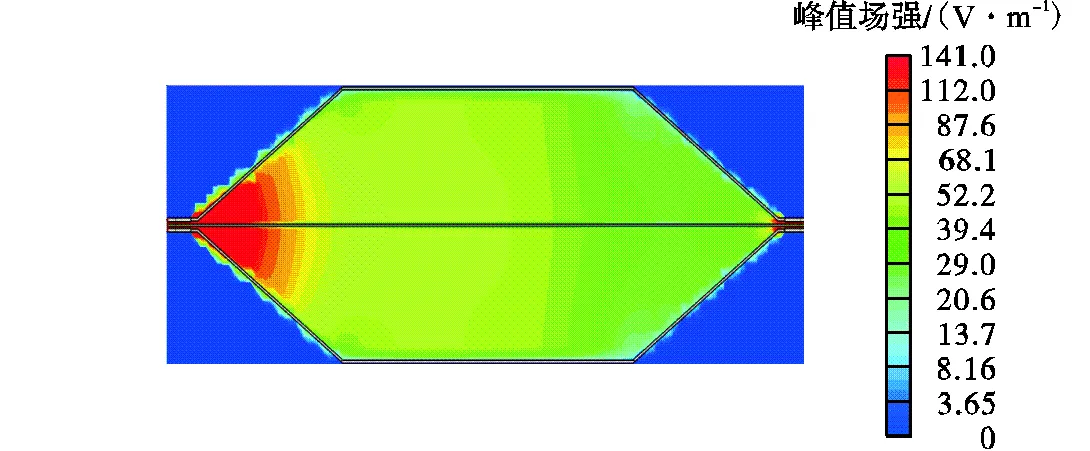
图4 4,ns TEM室场强分布

表1 不同位置点的场强仿真结果

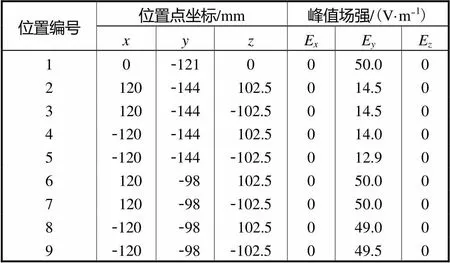
Tab.1 Numerical simulation results of electric field in different positions

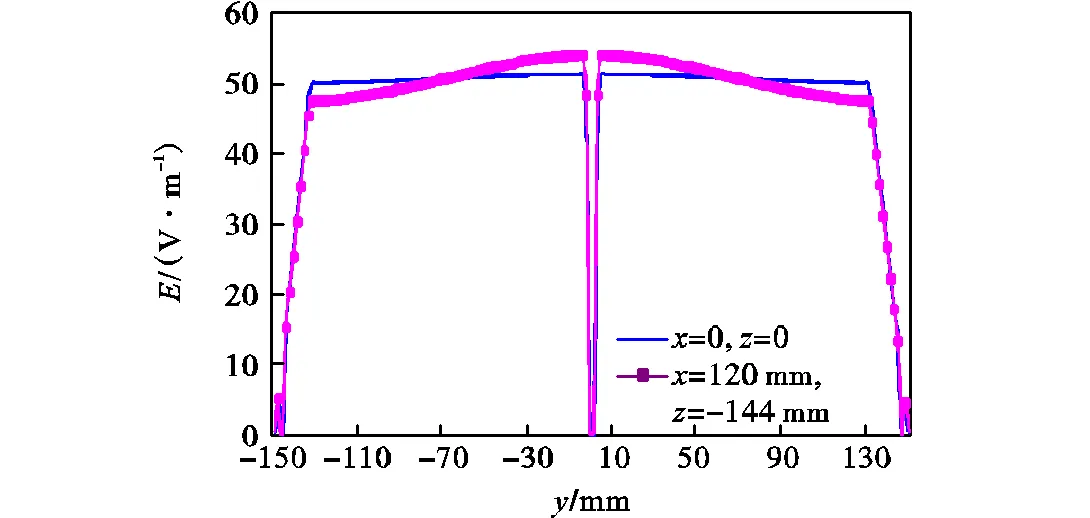
图5 沿y轴方向场强分布曲线

3 探头校准实验

采用电磁脉冲探头校准系统对D-dot探头进行实验，其实验布置如图6所示，脉冲信号源为EMC partner的瞬变脉冲产生器MIG2000-6，数字示波器型号为DPO7104C，带宽1,GHz，开放式TEM室高为14.7,cm，工作频段为DC-500,MHz，探头型号为montena SGE1G，其频率响应为1,GHz．

图6 探头校准系统

由于D-dot探头测量的输出信号为微分信号，需要通过积分器积分，现采用montena自带的硬件积分器将探头直接测量的微分信号积分后，在示波器上显示，其校准波形如图7(a)所示，黄色曲线为示波器测量TEM室输出端口衰减后的电压曲线，绿色曲线为积分后的校准曲线，探头测得的波形与小室内的场强波形基本一致，但是在前端出现尖峰，这是由于积分器的输入阻抗为50,W，输出阻抗为1,MW，积分器的分布参数导致信号过冲或波动，去掉积分器，将探头直接接示波器，示波器的阻抗设为50,W，将测量信号采用数值积分[13]，得到的波形如图7(b)所示，其中黄色曲线为TEM室输出信号，绿色曲线为探头测量的微分信号，粉红色曲线为采用数值积分还原信号，可以发现粉红色的波形幅值平坦稳定，过冲及波动现象消失，因此说明积分器阻抗不匹配会造成信号失真，在校准时应排除此部分的影响．

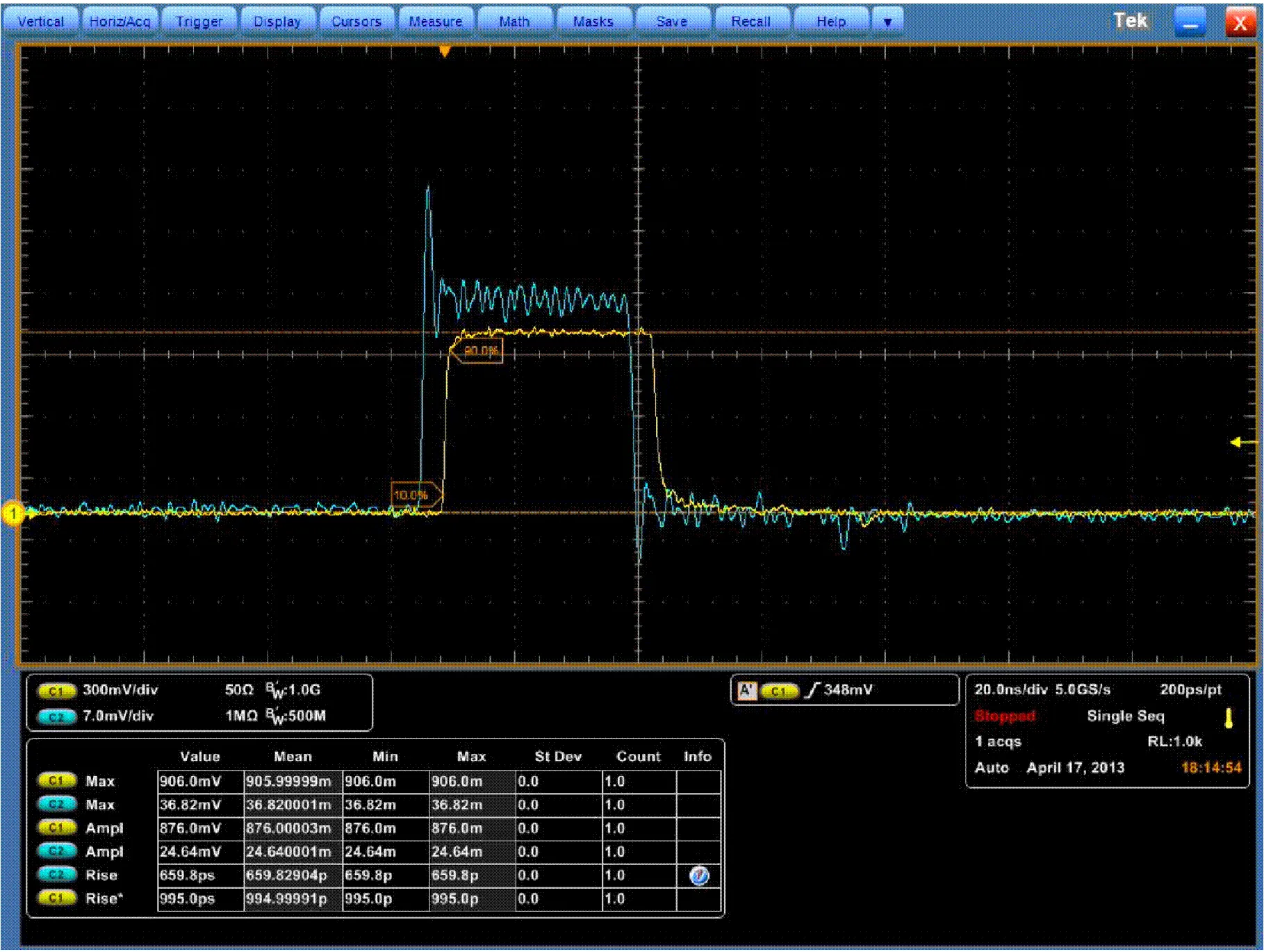
（a）采用硬件积分器的校准波形

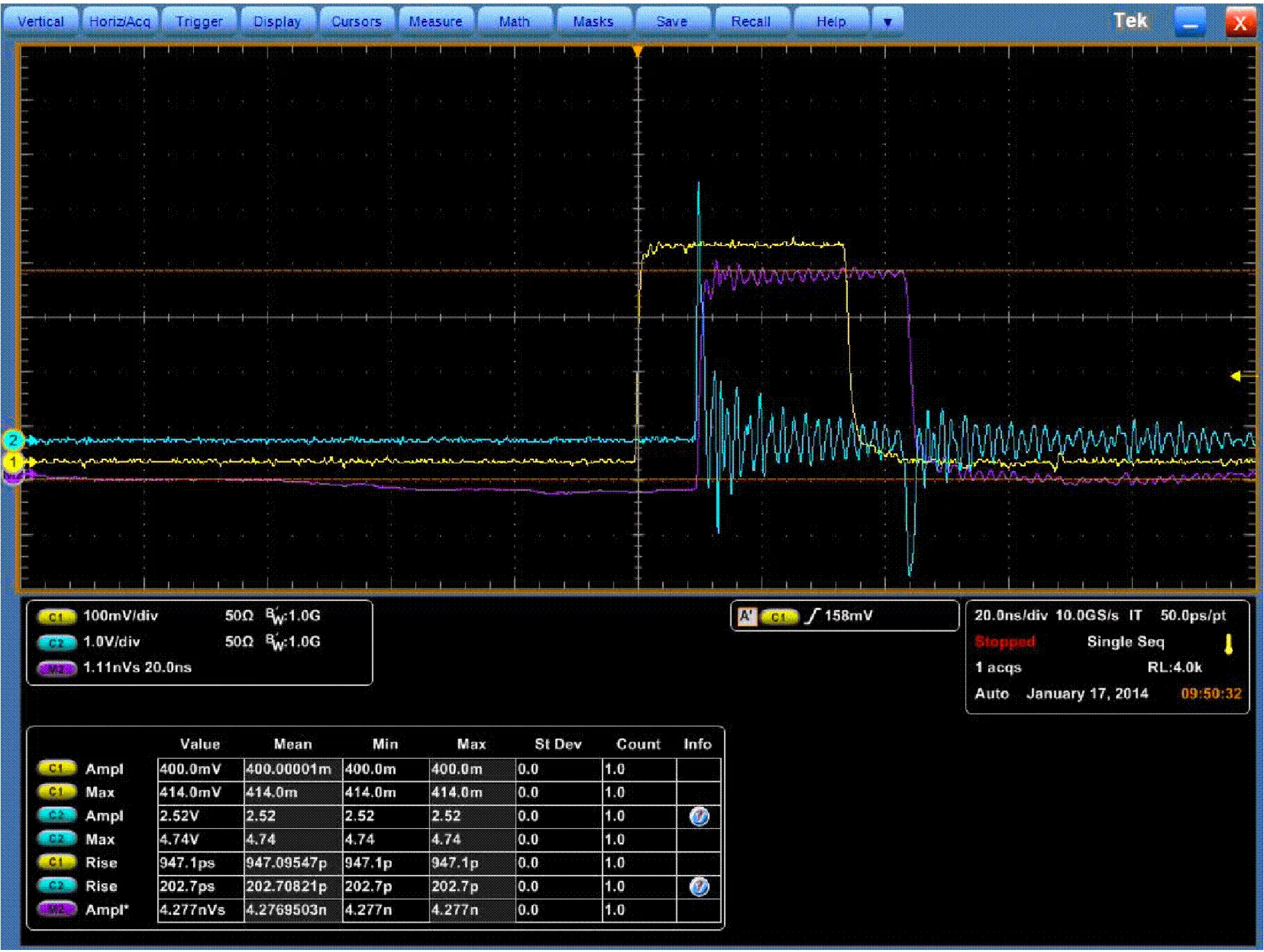
（b）采用软件积分的校准波形

图7 探头测试波形及小室输出端波形

Fig.7 Measurement waveforms of probes and waveform in output port of TEM cell

校准结果参数如表2所示，根据式(1)计算出修正系数，其校准结果与出厂值相同．

表2 SGE1G探头校准结果

Tab.2 Calibration results of probe SGE1G

4 校准系统性能验证

选取频响为3,GHz、型号为SGE1G探头的D-dot和光电探头两种不同类型的探头进行校准比较实验，分别从测试结果的重复性、线性度两方面相互验证探头与校准系统的性能．

4.1 重复性实验

使用相同的信号源，选取固定场强条件下，进行6次测量，实验结果如表3所示，采用实验标准偏差表征探头测量值的重复性．

重复性S计算式为

式中：x为参数的每次测量值；为参数的次测量的平均值；S表示重复性，S越小表示系统或探头测量的重复性越好，反之重复性越差．

表3 探头系数重复性实验结果

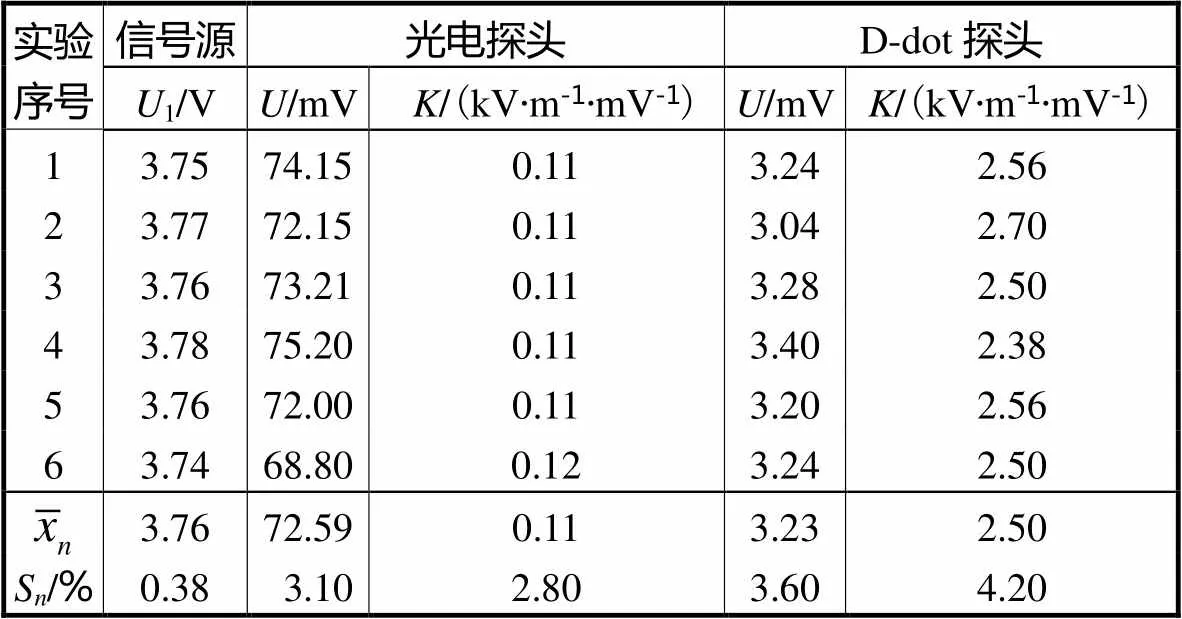
Tab.3 Repetitiveexperiment results of probe coefficients

根据以上测试结果可知，标准信号源输出一固定指示值的电压信号时，示波器多次测量此输出信号电压峰值的标准偏差较小为0.38%,，可以说明源的输出重复性较好，TEM室注入的信号非常稳定．光电探头和D-dot探头测量结果相比，光电探头的修正系数小，灵敏度高，重复性较小为2.80%,，校准用的标准场的重复性应小于2.80%,．

4.2 线性度实验

在不同场强条件下，光电探头和D-dot探头测量结果如表4所示，根据探头修正系数变化量L来判断，如果修正系数变化量越小则探头线性度越好，修正系数变化量越大线性度越差．其计算公式为

式中：K为各场强校准点计算的探头系数；K,max为各场强校准点的探头系数K中最大值；K,min为各场强校准点的探头系数K中最小值．

表4 探头系数线性度实验校准结果

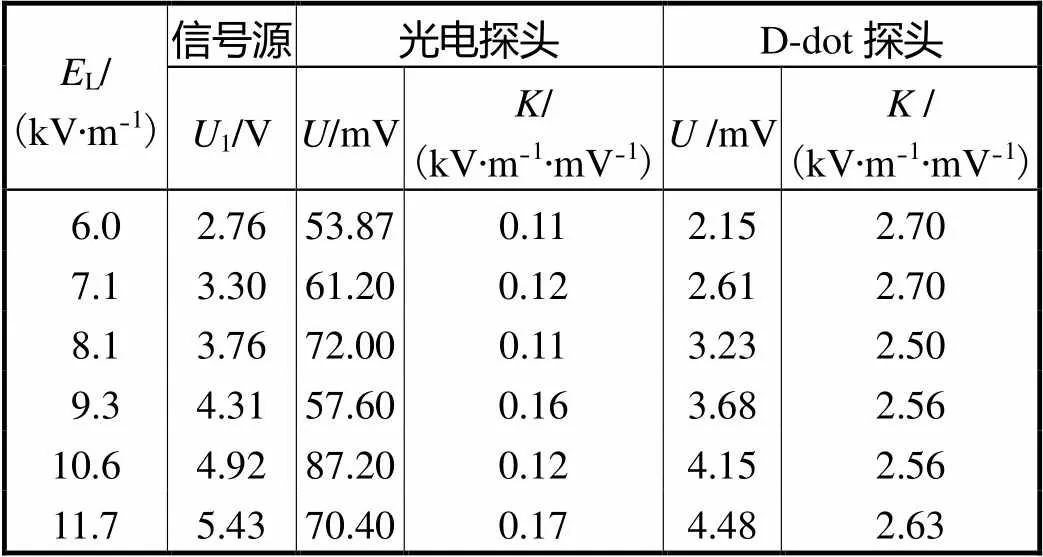
Tab.4 Linear experiment results of probe-coefficients

由表4可计算出光电探头修正系数变化量为20.2%，D-dot探头修正系数变化量为3.9%，由此可见，不同标准场强条件下，光电探头的修正系数不同，线性度较差，D-dot探头的修正系数不受场强大小的影响，从而可以推断在灵敏度允许的条件下，D-dot探头校准不受标准场幅度影响，而光电探头需要校准线性度．

5 校准系统的不确定度分析

校准系统的不确定度按照GUM方法进行分析，主要来源于以下几个方面：

(1) 示波器的电压幅度测量不准确所引起的不确定度，根据示波器计量证书知电压测量误差限为1%,，按照均匀分布，因此其不确定度分量为0.58%,；

(2) 示波器的采样率引入的测量不确定度为1.2%,；

(3)传输电缆和衰减器的衰减量引入的测量不确定度，根据矢量网络分析仪测量得到衰减量的扩展不确定度为3%,，因此其不确定度分量为1.5%,；

(4) 失配引入的测量不确定度分量服从U型分布为1.4%,；

(5) 其他不确定度分量来源如环境影响引入的测量不确定度、测量重复性引入的测量不确定度等．

综合评定后得到其校准系统的合成标准不确定度为4.2%,，其扩展不确定度为8.4%,．

6 结 论

(1) 电磁脉冲探头的校准采用一定宽度的脉冲激励信号，可以有效区分D-dot探头还原波形的尖峰，而此尖峰是由于硬件积分器阻抗不匹配所引起，为了减少校准误差，应读取具有一定脉冲宽度的电压值作为探头的测量值，或者采用数值软件积分方式还原测量信号波形．

(2) 从仿真实验结果可知，由于芯板和底板边缘效应的影响，靠近芯板和底板位置处场强随位置变化而变化较大．

(3) 采用D-dot探头和光电探头在此校准系统上进行重复性和线性度实验，从实验结果可知，校准系统的重复性优于2.8%,．采用GUM方法分析，校准系统的扩展不确定度为8.4%,．

［1］ Department of Defense. MIT-STD-461F—2007 Requirements for the Control of Electromagnetic Interference Characteristics of Subsystems and Equipment[S]. United States of America：AREA EMCS，2007.

［2］ Montena Company. Ground plane D-dot electric field sensor user’s manual[EB/OL]. http：//www. montena. com，2015-03-10.

［3］ 卫 兵，顾元朝，周荣国，等. 阳加速器水传输线D-dot的设计、标定和实验[J]. 强激光与粒子束，2007，19(5)：830-834.

Wei Bing，Gu Yuanzhao，Zhou Rongguo，et al. Design，calibration and experiment of D-dot at Yang accelerator in water transmission line[J].，2007，19(5)：830-834(in Chinese).

［4］ 付佳斌，卿燕玲，卫 兵，等. ns脉冲测量中的波形重建[J]. 强激光与粒子束，2010，22(11)：2759-2762.

Fu Jiabin，Qing Yanling，Wei Bing，et al. Reconstruc-tion of ns pulse waveform[J].，2010，22(11)：2759-2762(in Chinese).

［5］ 陈福深，陶厚超，孙 豹. 带双负载环形天线的集成光波导磁场探测器[J]. 电子科技大学学报，2009，38(1)：141-143.

Chen Fushen，Tao Houchao，Sun Bao. Integrated optical waveguide magnetic field probe with a doubly-loaded loop antenna element[J].，2009，38(1)：141-143(in Chinese).

［6］ 陈福深，张阜文. 分段电极LiNbO3光波导宽带微波电场接收器[J]. 微波学报，2005，21(5)：54-57.

Chen Fushen，Zhang Fuwen. An integrated optical waveguide E-field receiver at wide-band microwave with segmental electrodes[J].，2005，21(5)：54-57(in Chinese).

［7］ 曾 嵘，陈未远，何金良，等. 光电集成强电场测量系统及其应用研究[J]. 高电压技术，2006，32(7)：1-5.

Zeng Rong，Chen Weiyuan，He Jinliang，et al. Study on optical electric integrated electric field measurement system and application in high voltage measurement[J].，2006，32(7)：1-5(in Chinese).

［8］ Middelkoop R. Time-domain calibration of field sensors for electromagnetic pulse(EMP)measurements[J].，1991，40(2)：455-459.

［9］ 石立华，陶宝祺，周璧华. 脉冲磁场传感器的时域标定[J]. 计量学报，1997，18(2)：140-144.

Shi Lihua，Tao Baoqi，Zhou Bihua. Calibration of pulse magnetic field sensor in time domain[J].，1997，18(2)：140-144(in Chi-nese).

［10］ 陈 竞，石立华，李炎新，等. 光纤传输脉冲电场传感器的时域校准[J]. 安全与电磁兼容，2006，32(6)：86-88.

Chen Jing，Shi Lihua，Li Yanxin，et al. Time domain calibration of pulsed electric field sensors with fiber optic transmission system[J].，2006，32(6)：86-88(in Chinese).

［11］ 谢彦召，刘顺坤，孙沛云，等. 电磁脉冲传感器的时域和频域标定方法及其等效性[J]. 核电子学与探测技术，2004，24(4)：268-273.

Xie Yanzhao，Liu Shunkun，Sun Peiyun，et al. Calibration methodology of EMP sensor in time-domain and frequency-domain[J].，2004，24(4)：268-273(in Chinese).

［12］ IEEE Electromagnetic Compatibility Society. IEEE Std 1309—2005 IEEE Standard for Calibration of Electromagnetic Field Sensors and Probes，Excluding Antennas，from 9 kHz to 40 GHz[S]. New York：The Institute of Electrical and Electronics Engineers，Inc.，2005.

［13］ 张永强，宋建江，屠良尧，等. 软件数值积分误差原因分析及改进办法[J]. 机械强度，2006，28(3)：419-423.

Zhang Yongqiang，Song Jianjiang，Tu Liangyao，et al. Error analysis and improvement method when numerical integration with software[J].，2006，28(3)：419-423(in Chinese).

(责任编辑：孙立华)

Calibration System for Electromagnetic Pulse Probes

Liu Xingxun1, 2，Han Yufeng2，Zhang Tao1

(1．School of Electrical Engineering and Automation，Tianjin University，Tianjin 300072，China；2．China Beijing Institute of Radio Metrology and Measurement，Beijing 100058，China)

In order to meet the requirement of EMP probes calibration accurately，a calibration system based on standard field method for probes is established．The exciting signal of time domain is transformed in FFT and the characteristics of system in frequency domain are analyzed．According to the results of simulation，a measurement district can be confirmed in which the electrical field is uniform．Methods of measurement are researched with the measurement signal of probe integrated by integrator and software respectively．The repetitive experiment and the linear experiment on D-dot probe and photoelectricity probe are conducted using the proposed system．The experimental result shows that the repeatability of calibration system is better than 2.8%,，therefore the calibration problem of EMP probes can be solved effectively.

electromagnetic pulse；probe；calibration

10.11784/tdxbz201503025

TG156

A

0493-2137(2016)11-1175-06

2015-03-11；

2016-02-14.

国防科工局及航天科工集团第二研究院资助项目(JY20313).

刘星汛（1982—  ），女，博士.

刘星汛，xun_zi_jing@163．com.