地铁引起的站台邻近建筑室内振动预测分析

刘长卿

地铁引起的站台邻近建筑室内振动预测分析

刘长卿1，2

（1.上海市环境科学研究院，上海 200233；2.上海城市环境噪声控制工程技术研究中心（筹），上海 200233）

为了对地铁引起的站台邻近建筑楼层振动进行预测，提出并验证半经验半数值的振动预测方法，即运用实测经验法确定振源强度，有限元法分析建筑结构振动传递函数，将源强与传递函数相结合对建筑结构振动响应进行预测。利用半经验半数值的振动预测方法，对某地铁站台及其邻近建筑进行环境振动预测分析，得到地铁运行引起站台邻近建筑室内振动加速度级随楼层变化规律及其频谱特性。结果表明，半经验半数值的振动预测方法可行；地铁引起的站台邻近建筑内，随着楼层升高，低频振动受结构固有频率影响逐步放大，高频振动受阻尼影响能量衰减逐步减小，总振级随楼层增高呈先减小后增大趋势。该结果对地铁运行引起的站台邻近建筑室内环境振动预测及隔振设计具有实际意义。

振动与波；地铁站台；邻近建筑；半经验半数值法；环境振动预测

随着经济的快速发展以及城市规模的不断扩大，城市拥堵问题越来越严重。地铁可以有效缓解地面交通拥堵，但其列车运行引发的环境振动扰民问题也越来越受到人们的关注。近年来，国内外研究人员对地铁引起的振动问题做了大量研究工作。楼梦麟等利用地面振动实测及有限元分析法对地铁引起的周边建筑及地面振动传播规律进行了研究，得到了地铁振动不同频段的传播规律［1-2］。丁德云等针对地铁振动引起的地表低频响应进行了振动试验，并建立三维有限元模型预测地表低频响应，对影响地表低频响应的一些关键参数进行了评价［3］。刘维宁等在总结既有地铁环境振动预测方法基础上，指出了今后地铁引起的环境振动响应预测发展方向［4］。凌育洪等以某教学楼为例，研究了地铁引起的振动对多高层框架结构的影响以及钢弹簧隔振装置对该建筑的隔振效果，得到了一系列重要结论［5］。Gupta S等建立了有限元-边界元耦合模型用于地铁引起的振动预测，并用一系列实验测试验证了该数值模型预测振动的准确性［6］。Sanayei M等对地铁邻近建筑地基以及地面的振动进行了实测和频谱分析，为实际工程中建筑隔振设计提供一定的参考［7］。

随着上海等特大城市人口越来越密集，为了更加有效地利用土地资源，规划设计人员开始考虑在地铁站附近建设居民住宅，部分区域住宅建筑要紧邻地铁站台结构甚至与之相邻。这种情况下，地铁运行引起的结构振动及其辐射噪声对周边环境及适居条件的影响也给城市规划及设计人员提出了更大的挑战，规划设计前期的振动预测十分重要。目前常用的振动预测方法主要有有限元法和基于实测的经验法。有限元法可用于分析建筑本身的结构振动特性［8-10］，但在地铁引起的环境振动分析问题中，其激励源强度的确定是技术难点，目前尚无准确预测振动源强的数值方法，因此振动预测结果误差较大。实测经验法预测较为准确，但该方法耗费大量的人力物力，实际工程中执行起来较为困难。基于上述原因，本文将有限元法与实测经验法相结合，提出一种半经验半数值的方法，利用实测经验法对振动源强进行确定，结合有限元对结构振动特性的分析结果预测建筑振动响应。本文利用实测数据对该方法进行了验证，并利用该方法对实际工程中地铁引起的站台邻近建筑室内环境振动进行预测，得到该类环境振动问题的一些重要结论。本文的研究结果可以为地铁引起的环境振动预测及隔振措施的设计提供参考意见。

1　半经验半数值的振动预测方法

半经验半数值的振动预测方法，即利用实测方法获取振动源强，利用有限元法计算振动在地铁-土层-建筑结构中的传递特性及频率响应，得到振动响应的传递函数，将实测振动源强的频率谱与有限元计算得到的传递函数乘积得到结构的振动响应。

由于地铁引起的结构振动振幅较小，在小变形低应力的情况下，地铁结构及建筑结构均可看作线弹性体。土层为黏弹性体，其应变值一般为10-5数量级，因此可假设土层发生弹性变形，整个地铁结构-建筑-土层结构系统可看成线性系统［11］。线性系统结构动力学方程可以写为

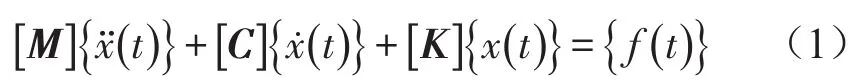
其中［M］，［C］，［K］分别是系统的质量矩阵，阻尼矩阵及刚度矩阵，｛f（t）｝是随时间变化的载荷向量，即振源激振力，而｛x（ t）｝则是系统振动响应向量。

实测振源激振力时程 f（）t经傅里叶变换可得到源强激励载荷频率谱

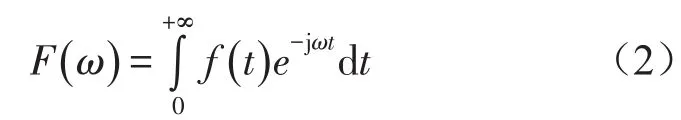
式中ω为振动频率。系统结构振动的频率响应以及系统振动响应时程分别可由式（3）、式（4）表达为

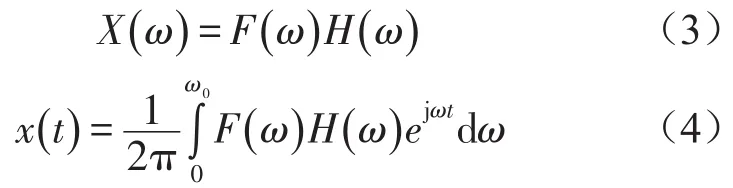
式中ω0为截止频率，H（）ω为系统频率响应传递函数，与结构本身的振动特性有关。因此在实测经验法获取足够的源强数据情况下，通过有限元分析求得系统频率响应传递函数即可获得系统最终的频率响应，预测建筑内振动水平。

2　地铁振动源强的确定

地铁运行过程中，列车与轮轨间的相互作用引起道床振动，并经由隧道结构传递到土层以及邻近建筑中。轨道道床作为振动的源头，其振动特性及振动强度对于环境振动的预测至关重要。振动源强特性与列车型号、车速、列车载重、道床结构、隧道结构形状以及周围地质条件等多种因素有关，准确地确定地铁振动源强成为环境振动预测的技术难点。

为了对地铁振动源强的特征进行研究，选取上海地区隧道结构条件相似的两条已通车地铁线路，进行轨道道床振动源强测试，道床测试点位如图1所示。测试过程中，采用ICP加速度传感器以及德国HEIM DATa Rec 4 Series 24通道数据采集仪连续采集5组列车经过时的道床振动加速度数据，其中列车车型相同，均为A型车。由于篇幅限值，仅给出线路1某一次列车通过时道床振动加速度时程曲线，如图2所示。

现行城市区域环境振动标准中，主要关注铅垂向振动的大小，通常采用振动加速度级（VAL）来评价不同频率振动的大小［12］，VAL单位为分贝（dB），可用下式（5）计算

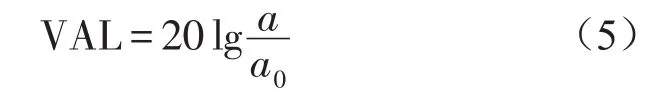
式中a为加速度有效值（m/ s2），a0=10-6m/s2为基准加速度。

将采集的振动加速度时程数据进行时频转换处理，并计算每组列车通过时的垂向振动加速度级频谱，两条线路各自的5组列车加速度级频谱以及5组列车的加速度级频谱平均值如图3—图5所示。由图可见：

图1　道床振动源强测点位置

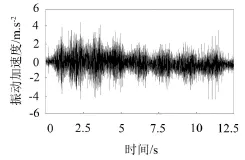
图2　线路1某列车经过时道床振动加速度时程曲线

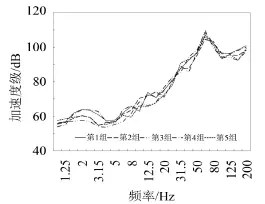
图3　线路1地铁道床处5组列车通过时振动加速度级频谱

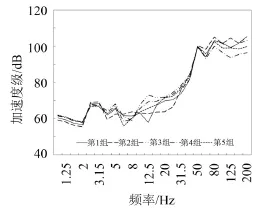
图4　线路2地铁道床处5组列车通过时振动加速度级频谱

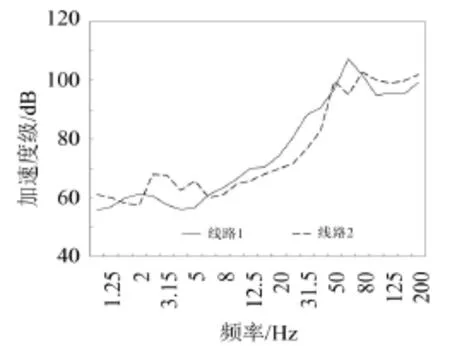
图5　两条线路地铁道床处5组列车振动加速度级均值频谱

1）同一条隧道不同组列车经过时，其道床振动加速度级随频率变化趋势一致，振动峰值所在频带相同，但由于不同组列车在载重、运行车速等方面存在差别以及其他偶然因素，其频谱曲线不能完全一致；

2）不同隧道的道床振动源强均值频谱曲线相似，受到土层条件影响，线路1的振动源强更大，且能量集中在63 Hz，线路2的振动能量集中于50 Hz 和80 Hz两个频率，二者主要振动能量均位于40 Hz～100 Hz范围内。

综上分析，相似结构的隧道，相同车型的列车运行引起的振动源强具有相同的频谱特性，其振动能量主要分布在40 Hz～100 Hz频率范围内，土层条件会影响源强幅值。对不同结构型式的隧道以及不同车型、车速等条件下的振动源强进行现场实测，总结出不同条件下振动源强频谱经验值，进而更加准确地预测建筑环境振动响应。

3　半经验半数值法的验证

为了验证半经验半数值法预测的准确性，以线路1某站台为例，建立地铁站台及其站厅层地下室整体结构有限元模型计算地铁振动引起的站厅层地下室振动传递函数，结合测试所得线路1振动源强，预测上层站厅地面振动值，与实测值对比验证。

3.1有限元建模

由于列车激振力引起建筑结构振动的振幅较小，在小变形低应力的情况下钢筋混凝土结构看作线弹性体，隧道周围土层看作黏弹性体，混凝土结构的周围土层具有黏性阻尼，振动能量在这里开始剧烈衰减，在变形较小的条件下，混凝土结构与周围土层之间不会出现相互分离的情况，故认为二者之间协同变形［13］。

根据上述假设条件以及地铁站台和站厅层地下室整体结构工程图，建立三维有限元模型如图6所示。地铁站台位于地下三层，站台上方为两层地下室。

图6　站台及地下室结构有限元模型

3.2计算结果

由于环境振动主要考察与地面垂直方向，计算过程中仅计算Z向的振动响应。该模型中的振源激励点位于轨道道床，响应点分别选取振源正上方地下2层两点、地下1层一点。振源点（A）以及各计算响应点（R1—R3）位置如图7所示。数值计算源强选取线路1五组列车通过时道床源强均值谱。将有限元计算结果与源强结合，得到R1—R3三点的振动响应。根据上海市发布的地铁引起的室内环境振动标准DB 31/T470-2009［14］规定的计权方式对计算结果进行频率计权，得到三个响应点的振动频谱如图8所示。由计算结果可见：

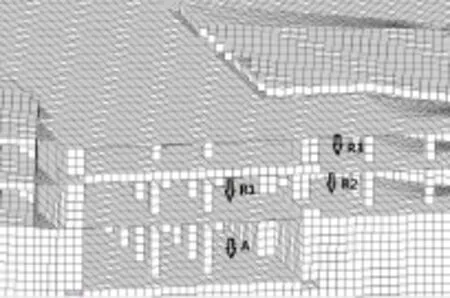
图7　振源点及响应点位图

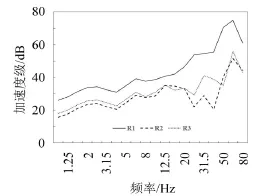
图8　振动响应频谱预测结果

1）由于R1处于站台正上方，其振动响应远大于R2、R3两点，而R2点虽然较R3距离振源更近，但其所在位置受土层支撑作用其结构阻抗较大，振动响应略小于R3点；

2）R1—R3三点频谱曲线具有良好的相关性，在10 Hz以下的较低频段曲线变化趋势几乎完全一致，这是由于低频振动响应与结构几何形状有关，而三点所处位置地下室结构型式相同，因此低频振动频谱相吻合，而高频段振动能量受到结构阻尼影响衰减较大，故三条曲线在较高频段分化较大。

3.3实测验证

为了验证数值计算的准确性，对该地铁站台和站厅层地下室进行振动测试。测点位置与有限元计算点位相同，分别测试各个测点Z向的振动加速度。采样频率为2 048 Hz，对各测点时域进行全纪录采样，测试结果进行频谱分析，计算1 Hz～80 Hz频率范围内的计权振级，将多组列车通过时的测试结果进行算数平均，计算得到各点的振动加速度级频谱如图9所示。由图9可见，实测R1—R3三点的振动响应谱具有良好的相关性，且曲线变化趋势与有限元预测结果相近。

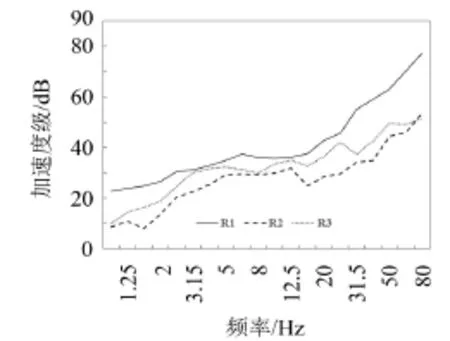
图9　振动响应频谱实测结果

对R1—R3三点的振动响应频谱预测值与实测值分别计算1 Hz～80 Hz范围内计权总振级，比较二者的总振级误差如表1所示。由表1可见，预测结果与实测结果相差3 dB以内，误差在可接受范围内，半经验半数值预测方法可行。

表1　预测结果与实测结果对比

4　工程预测分析

为了解实际工程中某地铁站台邻近的拟建建筑室内振动水平，运用本文提出的半经验半数值振动预测方法对该拟建建筑室内振动进行预测分析。

4.1工程概况

该拟建建筑位于上海市某地铁站邻近区域，为居住和商业混合区，地铁线路从建筑所在项目地块下方穿过，贴邻该建筑基础。建筑与地铁剖面位置关系见图10。拟建建筑地上部分共12层均为住宅，总高度40 m，地下室共2层均为机动车停车库和机电房，深度约10 m。地铁站台结构地下共五层，其中地下一、二层与建筑地下室层高相同，地铁站台位于地下五层，埋深约31 m。由于待分析拟建建筑地下结构与地铁站台结构贴邻，为防止地铁运行产生的振动对建筑影响过大，设计建筑地下室围墙与地铁站台外墙留出0.1 m间隙的隔振沟以密实砂土材料填充。地铁站区域设计最高车速50 km/h，列车为A型车，6节编组。采用60 kg/m钢轨，无缝线路，长轨枕式普通砼整体道床。该处地铁站台结构及车型、轨道等均与上文中线路1振源测试站台条件相似。

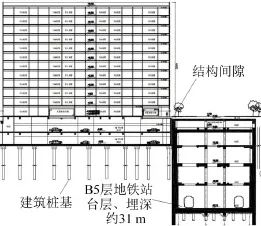
图10　建筑与地铁线路位置横剖面图

4.2计算模型

根据工程结构设计详图，建立待分析建筑及地铁站台、土层整体结构有限元模型，如图11所示。有限元模型中，住宅建筑及地下室采用板单元和梁单元组成框架结构，地铁站台及土层均采用块体单元。为减小土层边界反射波影响，模型边界采用黏弹性人工边界。钢筋混凝土结构材料参数按不同结构设计的混凝土等级分别取C 30和C 60混凝土的材料参数。土层类型根据该地块地质勘查报告及建筑抗震设计规范GB50011-2010［15］进行简化，土层等效参数见表2，其中ρ为土层密度，μ为泊松比，Vs为剪切波速，E为动弹性模量，可由ρ、μ、Vs计算得出［16］。建筑地下室与地铁站台外墙之间的隔振沟填充材料取密实中硬土的材料参数。激振力载荷施加在站台轨道道床处，沿行车线施加线激励单位载荷。

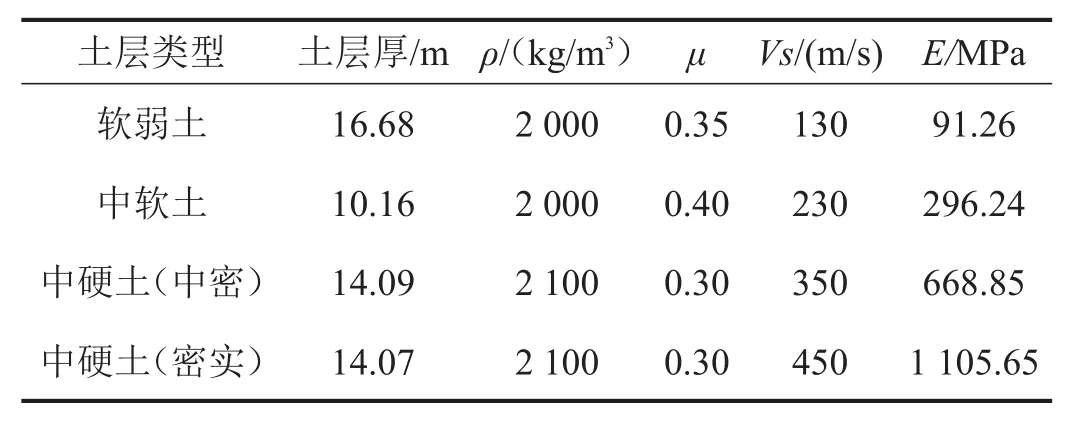
表2　土层等效参数

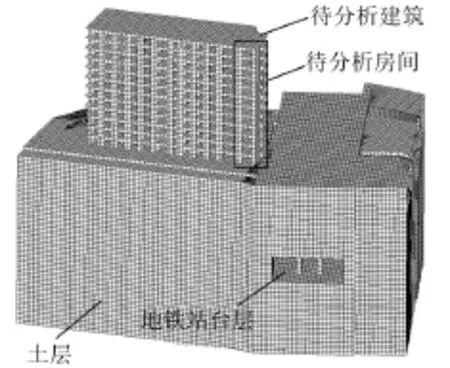
图11　整体结构有限元模型

4.3计算结果

对所建立的地铁站台-建筑-土层结构系统有限元模型进行分析得到建筑室内振动响应的传递函数。由于该处地铁站与上文中线路1源强测试的站台结构及列车、轨道条件相似，源强可选取线路1的实测源强频谱。利用半经验半数值法计算得到建筑室内各楼层的实际振动响应。本文主要针对靠近地铁站台一侧室内地板点的最大振动响应进行比较分析，图11中标出了待分析房间位置。

4.3.1楼层振动频谱分析结果

建筑部分楼层地板振动响应加速度级三分之一倍频程频谱曲线如图12所示，图中曲线为地铁源强激励下计算得到的部分楼层地板未计权的振动加速度级。由图12可见：

1）在8 Hz以下频率范围内，各楼层振动响应值较小，且曲线高度吻合，这是由于结构低频振动特性受结构几何形状影响较大，各楼层结构几何形状相似，且频率极低情况下振动随距离衰减缓慢，故频谱曲线接近重合；

2）在8 Hz～20 Hz范围内，楼层越高，频率响应越大，这说明低频振动在传递过程中衰减较慢，且随着楼层升高，结构固有频率逐步降低，在8 Hz～20 Hz频率区附近可能存在局部结构共振现象导致高层低频振动较大；

3）在20 Hz～40 Hz范围内，振动频谱曲线趋势一致，但峰值有所偏移，这是由于随着频率升高，结构阻尼等材料参数对振动频谱特性的影响增大，在该频段内结构几何形状和结构阻尼等材料参数均对振动响应产生较大影响；

4）在40 Hz以上，随着楼层升高，振动呈逐步减小趋势，说明在结构阻尼作用下，高频振动在传递过程中逐步衰减。

4.3.2总振级随楼层变化规律分析结果

根据DB 31/T470-2009，计算得到各楼层1 Hz～80 Hz计权加速度总振级，总振级随楼层变化曲线如图13所示。由图13可见，室内地板的计权总振级随着楼层升高整体呈先减小后增大趋势，其中1—6层总振级逐渐减小，6—12层总振级逐渐增大。这说明在较低楼层中高频振动能量占主导，随楼层升高，高频振动能量呈指数衰减，衰减速度较快，总振级逐渐减小。随着传递距离增加，在较高楼层中高频振动能量衰减速度减慢，而较高层结构振动固有频率偏低，低频振动随楼层升高逐步放大，其放大速度比高频振动衰减速度快，故而在较高层总振级随楼层升高逐渐增大。但总体而言，振动在随着楼层传递过程中能量有衰减，底层楼板振动总振级要大于顶层楼板。

图12　各楼层地板振动加速度级频谱

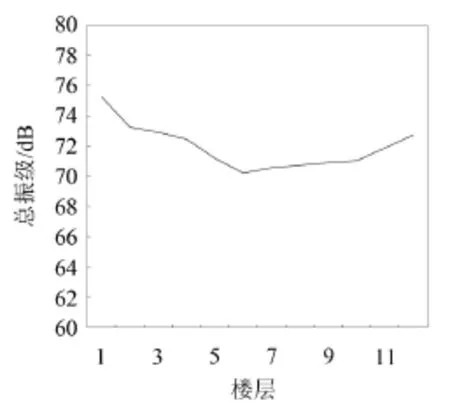
图13　各楼层地板总振级

5　结语

本文提出并验证了适用于地铁引起的站台邻近建筑振动预测的半经验半数值的分析方法，对地铁振动源强进行了实测分析，以上海市某地铁站台及其邻近拟建住宅建筑为背景，对地铁引起的站台邻近建筑振动规律进行了预测，得出以下结论：

（1）将振动源强的实测经验值与有限元计算的结构振动传递函数相结合的半经验半数值分析方法用于地铁引起的环境振动预测是可行的。

（2）相似结构的隧道，相同车型的列车运行引起的振动源强具有相同的频谱特性，其振动能量主要分布在40 Hz～100 Hz频率范围内，土层条件会影响源强幅值。

（3）受建筑结构几何形状、结构阻尼以及结构固有频率等条件影响，在8 Hz以下频率范围内，各楼层振动响应值较小，且频谱曲线接近重合；在8 Hz～20 Hz范围内，楼层越高，频率响应越大；在20 Hz～40 Hz范围内，振动频谱曲线趋势一致，但峰值有所偏移；在40 Hz以上，随着楼层升高，振动呈逐步减小趋势。

（4）室内地板的计权总振级随着楼层升高整体呈先减小后增大趋势，其中1—6层总振级逐渐减小，6—12层总振级逐渐增大，总体而言，振动在随着楼层传递过程中能量有衰减，底层楼板振动总振级要大于顶层楼板。

［1］楼梦麟，李守继.地铁引起建筑物振动评价研究［J］.振动与冲击，2007，26（8）：68-71.

［2］楼梦麟，贾旭鹏，俞洁勤.地铁运行引起的地面振动实测及传播规律分析［J］.防灾减灾工程学报，2009，29（3）：282-288.

［3］丁德云，刘维宁，李克飞等.地铁振动的地表低频响应预测研究［J］.土木工程学报，2011，44（11）：106-114.

［4］刘维宁，马蒙，王文斌.地铁列车振动环境响应预测方法［J］.中国铁道科学，2013，34（4）：110-117.

［5］凌育洪，吴景壮，马宏伟.地铁引起的振动对框架结构的影响及隔振研究-以某教学楼为例［J］.振动与冲击，2015，34（4）：184-189.

［6］GUPTA S，DEGRANDE G，LOMBAERT G.Experimental validation of a numerical model for subway induced vibrations［J］.Journal of Sound and Vibration，2009，321（3-5）：786-812.

［7］SANAYEI M，MAURYA P，MOORE J A.Measurement of building foundation and ground-borne vibrations due to surface trains and subways［J］.Engineering Structures，2013（53）：102-111.

［8］刘长卿，车驰东，吴庞.地铁振动对地面建筑物影响的数值分析与测试［J］.噪声与振动控制，2013，33（3）：188-193.

［9］孙晓明.地铁停车场上盖建筑的振动影响分析［J］.噪声与振动控制，2013，33（4）：177-181.

［10］张啟乐，刘林芽，李纪阳.曲线地段地铁振动对邻近建筑的影响分析［J］.噪声与振动控制，2015，35（4）：115-120.

［11］夏禾.车辆与结构动力相互作用［M］.北京：科学出版社，2005.

［12］中华人民共和国环保部.GB 10071-1988城市区域环境振动测量方法［S］.北京：中国标准出版社，1989.

［13］刘长卿，车驰东，朱瑞仪.城市交通高架轨道振动衰减的快速预测［J］.上海交通大学学报，2013，47（2）：242-247.

［14］上海市质量技术监督局.DB 31/T470-2009城市轨道交通（地下段）列车运行引起的住宅室内振动与结构噪声限值及测量方法［S］.上海：2010.

［15］中华人民共和国住房和城乡建设部.GB 50011-2010建筑抗震设计规范［S］.北京：中国建筑工业出版社，2010.

［16］李元松.高等岩土力学［M］.武汉：武汉大学出版社，2013.

In-door Vibration Prediction of the BuildingsAdjacent to Subway Station Platforms Induced by Subway Operation

LIU Chang-qing1，2
（1.ShanghaiAcademy of Environmental Sciences，Shanghai 200233，China；2.Shanghai Engineering Research Center of Urban Environmental Noise Control（in preparation），Shanghai 200233，China）

To predict the subway induced vibration of the buildings adjacent to the subway station platforms，a semiempirical and semi-numerical method is proposed and validated.In this method，the intensity of the vibration sources is determined by the empirical method and the vibration transfer function of the buildings is calculated by the finite element method.Combining the source intensity with the transfer function，the structural vibration responses are predicted.Then，the semi-empirical and semi-numerical method is applied to analyze the subway induced vibration in the adjacent buildings.The vibration level and its spectrum character of the floors in the buildings are predicted.The results show that the semiempirical and semi-numerical method is feasible.With the rise of the floor，the influence of the natural frequency of the structure on the low frequency vibration increases progressively，the high frequency vibration decreases progressively due to the damping effect，and the total vibration level decreases initially and then increases.This work may be helpful for the prediction of the subway platform induced vibration in adjacent building and the engineering design of vibration isolation.

vibration and wave；subway station platform；adjacent building；semi-empirical and semi-numerical method；environmental vibration prediction

X593；TB533

ADOI编码：10.3969/j.issn.1006-1335.2016.03.021

1006-1355（2016）03-0100-06

2015-12-29

上海市自然科学基金资助项目（15ZR1434800）

刘长卿（1989-），男，辽宁人，主要研究方向为环境振动与噪声控制。E-mail：liu-chq@163.com