舵轴位置对全动舵面气动弹性稳定性影响
史晓鸣,梅 睿,苏轶龙,梅星磊
舵轴位置对全动舵面气动弹性稳定性影响
史晓鸣,梅睿,苏轶龙,梅星磊
(上海机电工程研究所,上海 201109)
研究舵轴位置对全动舵面气动弹性特性的影响,用有限元方法分析舵面模态,当地流活塞理论计算非定常气动力,应用Lagrange方程,建立基于模态坐标运动方程。结果表明:当舵轴在根弦相对位置从前向后移动过程中,失稳形态由颤振转变为发散,并引起临界动压突变现象。失稳形态转变位置会随着攻角增大而逐渐后移。在转变位置之前,颤振临界动压随着舵轴后移,呈现先减小后小幅度增大趋势;在转变位置之后,发散临界动压随着舵轴后移单调减小。
振动与波;气动弹性;颤振;发散;舵轴位置;全动舵面
舵轴是舵机连接并操纵全动舵面的重要部件。目前在导弹工程设计中,主要是根据飞行包线内铰链力矩的分布进行舵轴位置设计,要求舵轴应尽量设计安排在使得铰链力矩较小的位置[1-3]。而舵轴位置的改变除了改变铰链力矩,亦将引起舵面模态的变化,对气动弹性稳定性产生影响。在工程设计中,增加刚度、施加配重等被动抑制方法是提高颤振边界的常用手段[4-7],但此类方法往往带来额外的质量,影响飞行器的总体指标性能。而在设计阶段合理地布置舵轴位置,提高全动舵面的气动弹性稳定性,则不需要付出“罚重”的代价。但目前探讨舵轴位置对舵面气动弹性稳定性影响的公开报道文献比较少。因此,研究舵轴位置对舵面气动弹性稳定性的影响对工程设计具有重要意义。
本文以有限元方法计算舵面模态,当地流活塞理论计算非定常气动力,分析研究来流马赫数M∞= 3,攻角α=0°、5°、10°、15°、20°工况下,舵轴位置在根弦总长30%~70%范围内变化对小展弦比后掠梯形舵面气动弹性稳定性的影响及变化规律。
1 计算方法
应用Lagrange方程,并忽略结构阻尼,舵面运动方程可写作

式中M、K分别为模态质量、刚度矩阵,ξ为模态坐标,Q为广义气动力

Δp为非定常压力分布,Φ为模态振型函数组成的列矢量,M∞、c∞、q∞为无穷远来流马赫数、声速、动压,B、C为广义气动力系数矩阵。
模态质量、刚度、振型等参数可通过有限元方法计算获取。超声速工况下,非定常压力分布应用当地流活塞理论[8,9]计算

ρL、cL为舵表面任意点的当地气流密度、声速,Wm为物面扰动引起的下洗,其具体表达式见文献[8],上述当地流参数通过CFD数值仿真求解。

在给定马赫数的情况下,计算不同动压下状态矩阵的特征值λ=σ+jω,根据特征值变化判断系统的气动弹性稳定性。随着动压增大,当实部σ由负变正时,系统失稳,此时的动压即为临界动压qcr,虚部为失稳频率ωcr,ωcr≠0为颤振失稳,虚部ωcr=0为发散失稳。
2 算例及分析
考察如图1所示舵面,根弦长275 mm、尖弦长140 mm、展长255 mm,前缘后掠角20°,材料2A12,舵轴位置在根弦总长的30%~70%范围内变化。首先利用有限元软件Nastran计算得到不同舵轴位置下的舵面模态参数,其中舵机传动机构在舵轴弯扭两个方向上的支撑刚度分别取ks=5×1011N/m、kα= 6×105N∙m/rad。图2给出了舵轴位置在根弦从前向后变化时,舵面前两阶频率f1、f2以及频率差f2-f1的变化,整体上前两阶频率均呈现先增大后减小的趋势,频率差则是单调递减。图3为前两阶振型节线的变化。
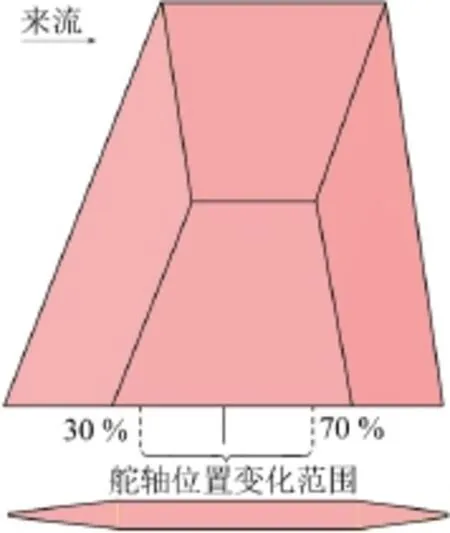
图1 舵面示意图
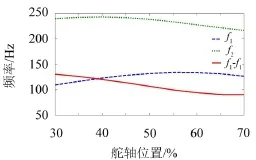
图2 频率随舵轴位置的变化
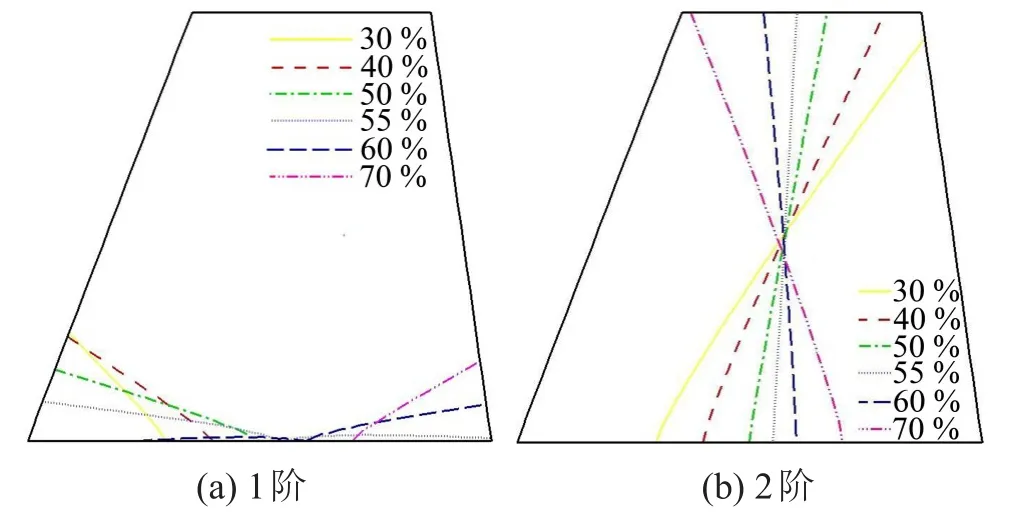
图3 振型节线随舵轴位置的变化

图4 临界动压随舵轴位置变化
以上述舵轴位于不同位置下的前两阶模态参数作为气动弹性分析的输入,分析来流马赫数M∞=3,密度ρ=0.336 2 kg/m3,攻角α=0°、5°、10°、20°状态下的失稳临界动压。从图4中可见,在不同攻角状态下,随着舵轴位置从根弦总长30%处逐渐后移,临界动压均呈现减小趋势,且均在根弦总长50%处达到最小;随着舵轴位置进一步后移,临界动压先小幅度增大后突然跳跃增至最大,然后再减小。
α=0°、5°、10°、15°状态下,临界动压随舵轴位置的变化规律基本相同。图5给出其中α=0°状态下,舵轴位置分别位于根弦总长30%、55%、60%、65%时,系统特征值实部σ、虚部ω随动压的变化。舵轴位于根弦总长30%~55%之间时,失稳形态均为颤振(图5(a)、图5(b));舵轴位于根弦总长60%时(图5(c)),q=8 320.5 kPa处,特征值实部σ有小幅度变正后又变负的小阻尼颤振现象,本文的计算忽略结构阻尼,实际飞行器总有一定的结构阻尼,因此实际情况下,此类小阻尼颤振并不会发生,实际的失稳临界动压应为qcr=12 506 kPa,失稳形态为发散,较之舵轴位于根弦总长30%~55%时,此时的临界动压大幅度跳跃上升;舵轴进一步后移至根弦总长65%之后,失稳形态已彻底转变为发散,无小阻尼颤振现象(图5(d))。

图5 系统特征值实、虚部随动压的变化(α=0°)
图6给出了α=20°状态下,舵轴位置分别位于根弦总长30%、60%、65%时,系统特征值实部σ、虚部ω随动压的变化。舵轴位于根弦总长30%~60%之间时,失稳形态均为颤振(图6(a)、图6(b));舵轴位于根弦总长65%之后,失稳形态为发散(图6(c))。
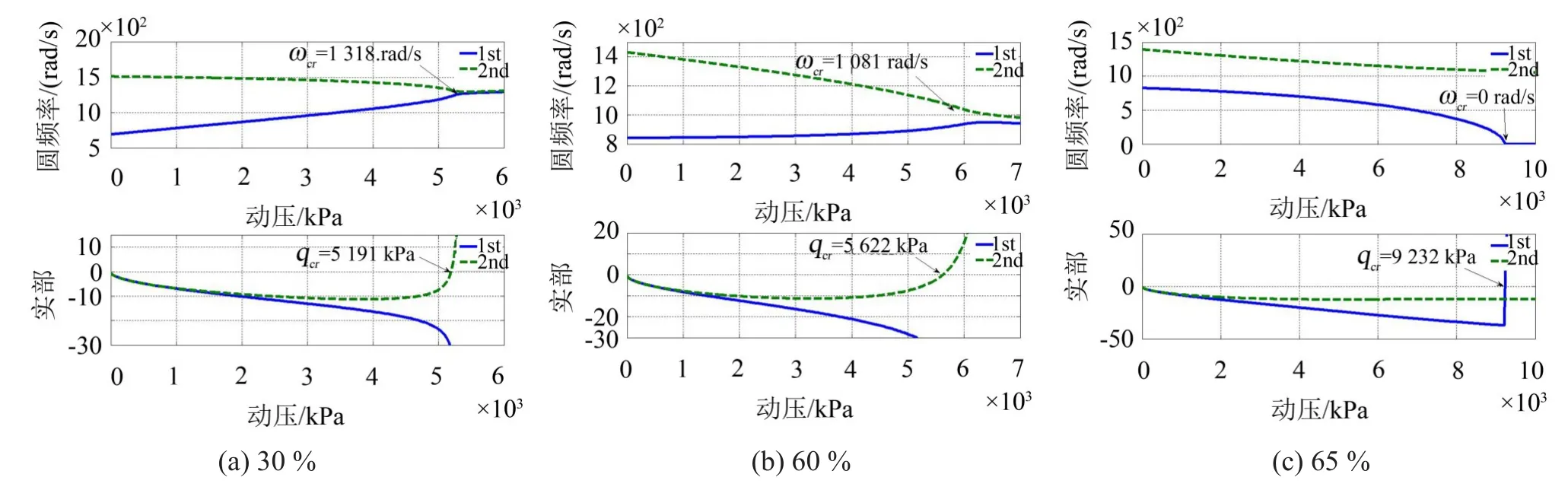
图6 系统特征值实、虚部随动压的变化(α=20°)
由上述分析可见,在舵轴后移过程中,临界动压突变增大至最大值的现象是失稳形态从颤振转变为发散所致。该失稳形态转变位置随着攻角增大而逐渐后移,α=0°、5°、10°、15°状态下,在根弦总长60%处失稳形态改变,而α=20°状态下,则后移至65%处。
这种失稳形态的改变是由于当舵轴处于相对靠前位置时,舵面各片条刚心相对靠前,发散动压较高,而质心相对于刚心靠后,颤振动压较低,故此刻更易发生颤振;而当舵轴处于相对靠后位置时,则是刚心相对靠后,质心相对靠前的,导致发散动压较低,颤振动压较高,故此刻失稳形态为发散。
在转变位置之前,当舵轴在根弦总长30%~50%间向后移动,从图2中可见,前两阶模态频率差f2-f1逐渐减小,故颤振临界动压单调递减。舵轴进一步后移至根弦总长55%时(α=20°大攻角状态下为60%),前两阶模态频率差f2-f1虽已接近最小值,但变化幅度已不大,且舵轴后移使得舵面各片条刚心后移,与质心相靠近,在此过程中,图3中前两阶振型节线已趋于纯弯与纯扭状态,振型的耦合程度削弱,故颤振临界动压又有小幅度回升。
在转变位置之后,随着舵轴进一步向后移动,各片条刚心进一步后移,在气动中心位置不变的情况下,两者间距进一步增大,故发散临界动压单调下降。
3 结语
本文研究舵轴在全动舵面根弦的相对位置变化情况下的舵面气动弹性特性,得到如下结论:
(1)全动舵面的气动弹性特性随着舵轴在根弦的相对位置变化而改变,当舵轴从前向后移动时,失稳形态由颤振转变为发散,并造成临界动压的突变。
(2)在失稳形态转变位置上,舵面的失稳临界动压最大;且该位置会随着攻角增大而逐渐后移。
(3)在转变位置之前,随着舵轴的逐渐后移,前两阶模态频率差逐渐减小,颤振临界动压逐渐减小,当舵轴进一步后移,前两阶模态频率差接近最小值,且变化幅度不大,但舵轴后移使得舵面各片条刚心后移,与质心相靠近,此时颤振临界动压又有小幅度回升。
(4)在转变位置之后,随着舵轴后移,舵面各片条刚心进一步后移,发散临界动压单调减小。
[1]樊会涛.空空导弹方案设计原理[M].北京:航空工业出版社,2014.
[2]许椿荫.防空导弹结构与强度[M].北京:宇航出版社,1993.
[3]余旭东.导弹现代结构设计[M].北京:国防工业出版社,2007.
[4]ROBERT E D,GEORGE A W.Flutter prevention handbook:a preliminary collection.Part B:Aerodynamic and mass balance effects on control surface flutter[R]. NASA/TP-2006-212490/VOL2/Part 2.
[5]高文杰.结构参数对无轴承旋翼悬停气弹稳定性的影响[J].噪声与振动控制,2012,32(4):18-22.
[6]刘济科,杨智春,赵令诚.利用配重改善平尾颤振特性方法的研究[J].强度与环境,1995,22(4):37-40.
[7]程芳,郭润江,霍应元.前缘变配重颤振分析[J].计算机辅助工程,2006,15(增刊1):56-58.
[8]史晓鸣,杨炳渊,李海东,等.基于当地流活塞理论的翼-身组合体飞行器大攻角超声速颤振分析[J].空气动力学学报,2012,30(5):664-667.
[9]张伟伟,叶正寅.基于当地流活塞理论的气动弹性计算方法研究[J].力学学报,2005,37(5):632-639.
Influence of Rudder Shaft Location onAeroelastic Stability of an All-moving Rudder
SHI Xiao-ming,MEIRui,SU Yi-long,MEI Xing-lei
(Shanghai Electro-mechanical Engineering Institute,Shanghai 201109,China)
Influence of rudder shaft location on the aeroelastic characteristics of an all-moving rudder is investigated. The modals of the rudder are analyzed by means of finite element method.unsteady aerodynamic force is calculated using local piston theory.The dynamic equations are established based on Lagrange's equation.Results show that the destabilizing form changes from flutter to divergence with the rudder shaft location moving along the root chord from the leading edge to the trailing edge.The location of the destabilizing form changing moves backward with the increasing of the attack angle. The flutter critical dynamic pressure decreases initially and then increases slightly with the rudder shaft moving backward in front of the changing location.While the divergence critical dynamic pressure decreases monotonously with the rudder shaft moving backward behind the changing location.
vibration and wave;aeroelasticity;flutter;divergence;rudder shaft location;all-moving rudder
V211.4
ADOI编码:10.3969/j.issn.1006-1335.2016.03.017
1006-1355(2016)03-0081-04
2015-11-18
上海市科委青年科技启明星资助项目(14QB1402400)
史晓鸣(1981-),男,江苏苏州人,高级工程师,博士,主要研究方向为飞行器结构动力学、气动弹性力学。E-mail:daybreakxmshi@126.com

