电磁流量计励磁线圈优化
张昊,岳士弘,张玉静,王化祥
电磁流量计励磁线圈优化
张昊,岳士弘,张玉静,王化祥
(天津大学电气与自动化工程学院,天津,100072)
从励磁线圈作用场的权重函数出发,按照磁通密度沿中轴线分布的均匀度、沿测量管轴方向分布的均匀度和整个空间分布的均匀度3个指标,确定最佳的励磁线圈形状。在用料以及励磁条件相同的情况下,对不同形状励磁线圈产生的感应电动势与被测液体的流速以及管道中液面高度的关系进行仿真分析。研究结果表明:圆形贴管壁的线圈励磁磁场均匀度最佳。实际应用中,要根据被测液体在管道中液面高度的状态选择最佳的励磁线圈形状。
电磁流量计;磁场均匀度;线圈优化;磁场强度;权重函数
电磁流量计是工业过程参数测量中广泛应用的一种流量仪表,具有结构简单,流量测量不受流体的密度、温度、压力、黏性等影响,测量范围大,原理上是线性的且测量精度高,使用可靠,维护简单等特 点[1−2]。但是,传统的电磁流量计由于系统本身结构的限制,监测到的信息量有限,使测量精度受到限制。由于励磁线圈有限长,使得励磁磁场不均匀,同时会在管道轴向平面内产生涡流,流体中电涡流的存在不可避免地影响测量精度。励磁系统的优化,是在相同的励磁条件下使得励磁磁场的强度和磁场均匀性增强。
电磁流量计电极两端测量电压的计算公式如下:
其中:下标a和b代表电极两端;为测量管半径;
为流体速度;为磁感应强度;为权函数。当和流体速度都是常数,权函数为1时,式(1)化为
但实际上,管道中的流体流动时,电极两端的电压是由流体微元进行切割磁力线的运动产生。和都是与位置,和有关的函数,而且每个微元对ab的贡献(权重函数)不一样。若不考虑权重函数,要保持磁场沿轴分布均匀,须采用轴长足够长的励磁线圈,这在实际应用中难以实现,电磁流量计正在向非均匀方向发展,因此,必须要考虑权重函数。
权重函数是一个与磁场分布和速度分布无关,仅与测量管尺寸、电极的几何形状、流体的性质有关的空间函数。SHERCLIFF[3]给出了二维平面上权重函数分布表达式为
上述权重函数的分布只有在管道和电极无限长时成立,很难在实际中应用。BEVIR将二维权重函数分布扩展到三维中,得出了三维权重矢量分布[3]。将式(3)分解成坐标轴分量的形式,得
W沿管轴方向的分布情况如图1所示。从图1可知:W随着离开电极所在截面的距离()增大而迅速衰减,当距离>0.25(为管道直径)时,W实际上达到0。这说明在离电极平面较远处的管内空间,流体产生的感应电势对电极间的输出信号基本上没有贡献[4]。因此,只须保证磁场在±0.25范围内在一定程度上保持均匀,即可近似为均匀磁场。这样,励磁线圈和传感器长度都可以缩短,从而使整个传感器的周长和体积大大缩小,质量也大大减轻。基于权重函数,可以在comsol软件中进行励磁线圈的模拟仿真,以便对各种线圈进行对比分析。
图1 权重函数在轴上的分布
Fig. 1 Distribution of weight function on axis
1 励磁线圈的形状及磁场仿真
1.1 应用背景
工业应用中,被测液体的流速范围一般在0.3~ 2.0 m/s,电极两端的感应电动势最大50.00 mV,最小0.10 mV,这样的信号非常弱,还要考虑噪声的干扰,有时噪声幅值甚至会超过被测信号的幅值[5−8]。传统的电磁流量计很难达到比较高的测量精度。为了提高测量的准确度就要尽量增强励磁磁场的强度以及磁场的均匀性,使得电极两端的感应电动势增强[9−11]。在同样的励磁条件以及线圈用料相同的情况下,可以绕制成多种形状的励磁线圈,通过比较产生的磁场均匀性以及磁场强度,可以选出最佳的励磁线圈形状。
1.2 3种形状励磁线圈磁场仿真
励磁线圈的形状常见的有圆形、菱形和马鞍形3种。对相同用料下不同形状励磁线圈产生的磁场的强度以及均匀度进行仿真比较。3种励磁线圈的形状如图2所示。
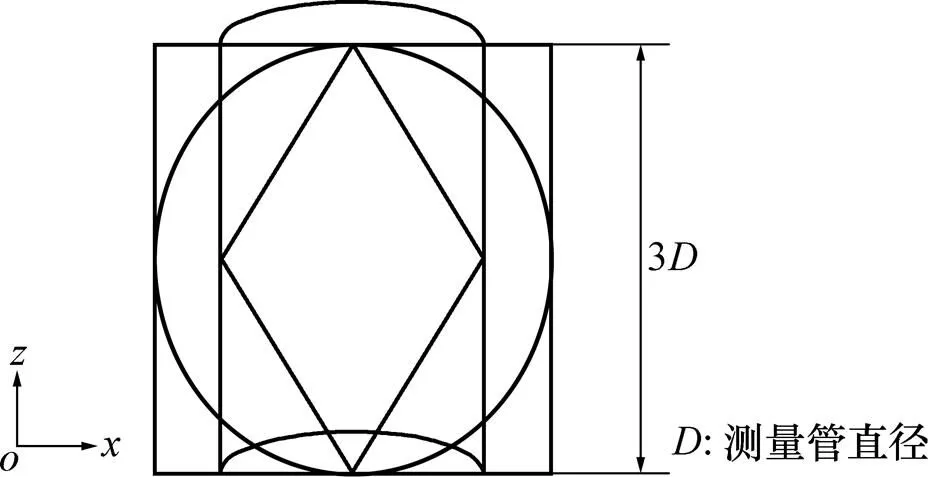
图2 3种励磁线圈形状
为保证用料相同,以圆形的周长为1 m,按比例绕制马鞍形和菱形的线圈。将马鞍形、圆形和菱形线圈分别贴到管壁上,令线圈轴向长度与用料相同,且被测液体流速均为1m/s。其中,具体仿真参数设置 如下:
1) 管道参数。管道直径为100 mm,管壁厚度为10 mm,管道长度为220 mm。
2) 线圈参数。线圈宽度厚度为10 mm,线圈轴长为150 mm。
3) 励磁参数。圆形线圈为200匝,菱形为273匝,马鞍形为185匝,励磁电流为1 A。
所得的仿真结果如表1所示。
表1 不同形状励磁线圈的磁场仿真结果
Table 1 Simulation results of magnetic field induced by different shapes of coil T
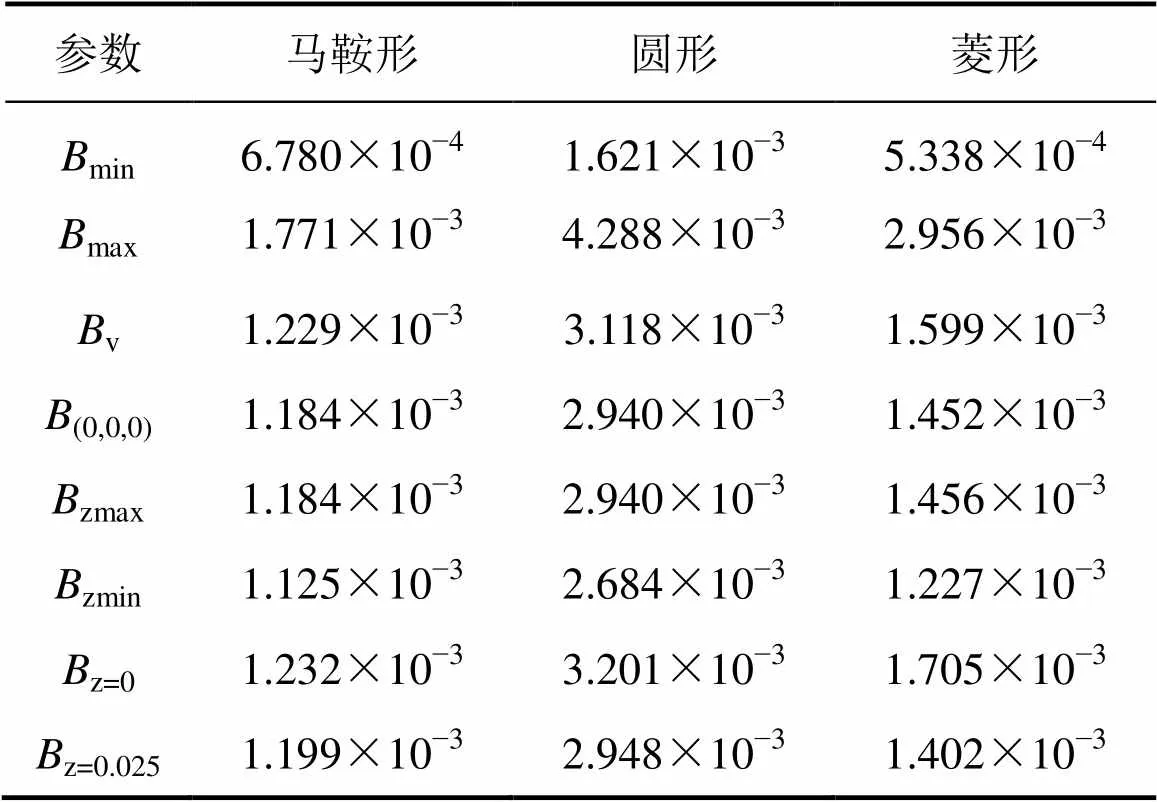
注:min和max分别为整个磁场空间磁场强度最小值和最大值;v为整个磁场空间磁场强度平均值;(0,0,0)为点(0,0,0)处磁场强度;Bmax为轴最大磁场强度;Bmin为轴最小磁场强度;B=0为−y=0平面内磁场强度平均值;B=0.025为−y=0.025平面内磁场强度平均值。
1.3 数据分析
为了对仿真结果进行分析对比,定义了3个指标1,2和3。
1)1为磁通密度沿中轴线分布的均匀度,表达式为
2)2为磁通密度沿测量管轴方向分布的均匀度,表达式为
3)3用来描述磁通密度在整个空间分布的均匀度,表达式为
表1所示为在励磁线圈轴向长度相同、用料相同及励磁条件相同下进行仿真所得结果。对3种线圈的磁场进行计算,各自对应的3个指标1,2和3如表2所示。
表2 指标分析
Table 2 Analysis of index

结合表1与表2,分析可得:
1) 圆形,菱形线圈产生磁场磁通密度较大,马鞍形相对较小。磁通密度由大到小为
circle>diamond>saddle(8)
2)1越接近0,表示磁通密度沿中轴线分布越均匀。由表2可以看到3种励磁线圈均匀度ε1的由小到大为
1saddle<1circle<1diamond(9)
3)2越接近0,表示磁通密度沿测量管轴方向分布越均匀,3种励磁线圈均匀度ε2的由小到大为:
2saddle<2circle<2 diamond(10)
4)3越接近0表示磁通密度在整个空间分布越均匀,3种励磁线圈均匀度ε3的由小到大为:
3circle≈3saddle<3 diamond(11)
综上可以得出如下结论:
1) 结合表1所得数据,分别从磁通密度和磁场均匀度2个方面进行比较分析,可以看出圆形励磁线圈的励磁效果最好。
2) 圆形和马鞍形线圈产生的励磁磁场的磁通密度沿中轴线分布较均匀;马鞍形线产生的励磁磁场的圈磁通密度沿测量管轴方向分布较均匀;圆形线圈产生的励磁磁场的磁通密度在整个空间分布较均匀;而菱形线圈产生的励磁磁场的磁通密度沿各个方向都最不均匀。
综上所述,圆形励磁线圈的励磁磁场均匀度最好。在条件相同情况下,计算利用圆形线圈励磁的测量精度比传统的马鞍形线圈励磁的测量精度提高了10.3%。
2 感应电动势与被测液体流速及液面高度的关系
2.1 应用背景
在实际工程应用中,电磁流量计管道中的被测液体不能保证总是处于满管的状态,液体的流速也不断变化。传统的流量计是按照始终保持满管并且流速不变的前提计算流体流量,这对电磁流量计的测量精度有很大影响[12−13]。随着管道中被测液体高度以及流速的变化,线圈两端产生的感应电动势会随之改变[14],这种变化是否是线性的需要分析,然后根据对应关系进行相应的线圈形状的选择。最近,电磁流量计的研究又出现了一些引人注目的新成果,如部分流管和锥形管内流量计[15−19]。
2.2 3种线圈感应电动势线性度分析
对于3种形状的线圈,在用料相同,励磁情况相同的情况下,分别仿真其在不同流速及不同液面高度的情况下的感应电动势。
以圆形线圈(254匝)为基准,保证用料相同,马鞍(200匝),菱形(238匝),励磁电流为1 A,线圈轴向长度为100 mm,管道口径为100 mm。流速范围为0.6~2 m/s,液面高度为10~100 mm。利用comsol进行仿真,对所得数据利用matlab进行绘制,结果分别如图2~4所示。
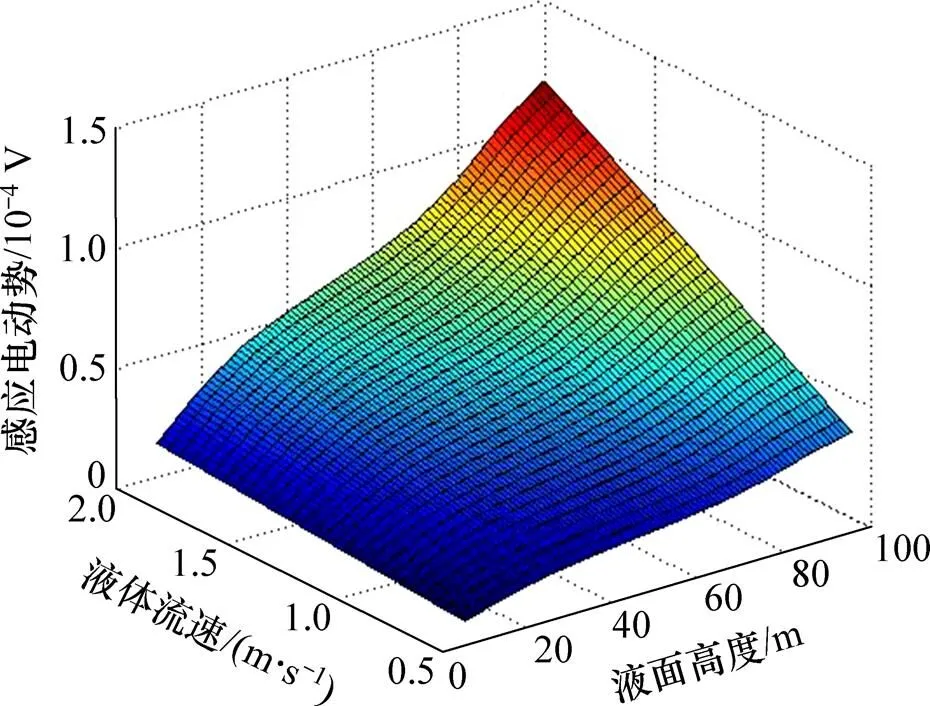
图3 马鞍线圈感应电动势与流速和液面高度关系

图4 圆形线圈感应电动势与流速和液面高度关系
通过对仿真数据及matlab图的分析可以看出:不同形状的线圈感应电动势与流速和液面高度不呈线性变化。在流速确定的条件下,对感应电动势和液面高度的关系,以及在液面高度确定的条件下感应电动势与流速的关系进行仿真分析,确定出不同条件下感应电动势的关系。仿真结果如图6和图7所示。
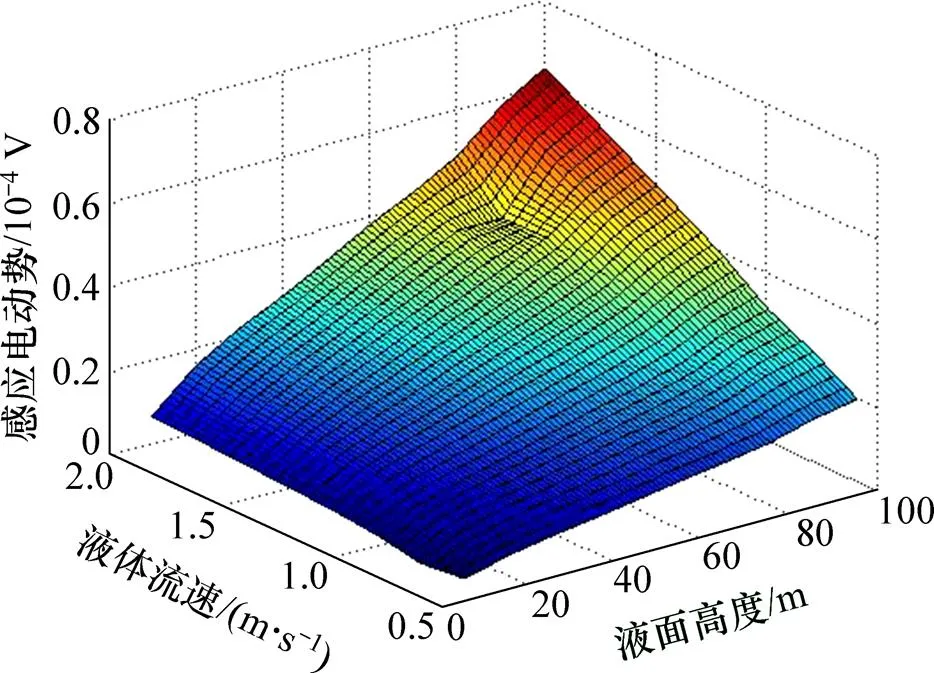
图5 菱形线圈感应电动势与流速和液面高度关系

流速/(m∙s−1):(a) 0.6;(b) 2.0

液面高度/mm:(a) 30;(b) 100
由图6可见:感应电动势与液面高度呈非线性 关系。没有一种励磁线圈形式对于所有的流动状态都最优。当液面高度低于管径的一半(50 mm)时,圆形线圈产生的感应电动势最大;当液面高度超过管径的一半时,马鞍形线圈产生的感应电动势最大。由图7可见:感应电动势与流速的关系呈线性关系,同时,也说明了满管时马鞍形线圈感应电动势大,低于半管时圆形线圈产生的感应电动势大。因此,在实际应用中,应该根据被测液体长时间所处的液面高度选择最佳的励磁线圈形状,从而获得尽可能大的感应电动势并节约经济成本,消除噪声对测量信号的影响。
3 总结
1) 电磁流量激励磁系统的设计原则是管道截面内的激励磁场分布尽可能均匀,管道内的磁场沿管道轴线的分布尽量均匀,并且要尽量提高磁场强度。
2) 在条件相同情况下(管道直径为100 mm,励磁电流为1 A),圆形励磁线圈(线圈宽度厚度为10 mm,线圈轴长为150 mm)的励磁磁场均匀度最好。所得到结果对于电磁流量计的设计和开发具有一定的参考和应用价值。
[1] HAYT W H, BUCK J A. Engineering electromagnetics[M]. New York: McGraw-Hill, 2001: 126−139.
[2] 冯慈璋, 马西奎.工程电磁场导论[M]. 北京: 高等教育出版社, 2000: 1−30. FENG Cizhang, MA Xikui. Introduction to engineering electromagnetic field[M]. Beijing: Higher Education Press, 2000: 1−30.
[3] 蔡武昌, 马中元, 瞿国芳, 等. 电磁流量计[M].北京: 中国石化出版社, 2004: 3. CAI Wuchang, MA Zhongyuan, QU Guofang, et al. Electromagnetic flow meter[M]. Beijing: China Petrochemical Press, 2004: 3.
[4] 卫开复, 李斌. 非满管电磁流量计权重函数有限元数值分析[J]. 自动化仪表, 2011, 33(9): 69−71. WEI Kaifu, LI Bin. Non-full pipe electromagnetic flowmeter weighting function finite element analysis[J]. Automation Instrumentation, 2011, 33(9): 69−71.
[5] 孔令富, 王月明, 李英伟, 等. 两相流下电磁流量计感应电势仿真研究[J]. 计量学报, 2013, 34(4): 339−344. KONG Lingfu, WANGYueming, LI Yingwei, et al. Potential electromagnetic flowmeter under two-phase induction simulation study[J]. Journal of Measurement, 2013, 34(4): 339−344.
[6] 王经卓. 电磁流量计权函数的数值仿真与验证[J]. 仪器仪表学报, 2009, 30(1): 132−137. WANG Jingzhuo. Numerical simulation and verification of weight function of electromagnetic flow meter[J]. Chinese Journal of Scientific Instrument, 2009, 30(1): 132−137.
[7] 张小章. 电磁流量计工作磁场的计算及测量[J]. 计量技术, 1990(9): 4−6. ZHANG Xiaozhang. Calculation and measurement of electromagnetic flowmeters working magnetic field[J]. Journal of Measurement Technology, 1990(9): 4−6
[8] XIA Yuming, XU Zhiqiang. Electromagnetic flowmeter measurement and numerical computation of laminar flow transport pipeline flow quantity[C]//Proceeding of the Second International Symposium on IEEE. Nanchang, China: ISECS, 2009: 169−173.
[9] 黄安贻, 杨硕. 非均匀磁场电磁流量计磁场的计算与分析[J]. 自动化应用, 2011(2): 56−58. HUANG Anyi, YANG Shuo. Calculation and analysis of non-uniform electromagnetic flowmeter magnetic field[J]. Automation Application, 2011(2): 56−58.
[10] 张小章, 孙向东. 电磁流量计磁场的设计[J]. 计量技术, 2010(8): 6−9. ZHANG Xiaozhang, SUN Xiangdong. The design of magnetic field of electromagnetic flow meter[J]. Journal of Measurement Technology, 2010(8): 6−9.
[11] BAKER R C. Numerical analysis of the electromagnetic flowmeter[C]//Proceedings of IEEE Electrical Engineers. Taibei, Taiwan: IET Digital Library, 1973, 120(9): 1039−1043.
[12] MICHALSKI A, STARZYNSKI J, WINCENCIAK S. 3-D approach to designing the excitation coil of an electromagnetic flowmeter[J]. IEEE Transactions on Instrumentation and Measurement, 2002, 51(4): 833−839.
[13] 滕涛, 刘娟, 王延军, 等. 外流式电磁流量计磁场分布的仿真研究[J]. 石油仪器, 2008, 22(5): 6−8. TENG Tao, LIU Juan, WANG Yanjun, et al. Simulation and research on magnetic field distribution of outflow electromagnetic flowmeter[J]. Petroleum Instrument, 2008, 22(5): 6−8.
[14] O’SULLIVAN V T, WYATT D G. Computation of electromagnetic flowmeter characteristics from magnetic field data. III. Rectilinear weight functions[J]. Journal of Physics D: Applied Physics, 1981, 14(14): 373−388.
[15] DU Qingfu, REN Wenjian, LIU Hai, et al. The design and implementation of low power electromagnetic flowmeter with trapezoidal excitation mode[J]. Metallurgical and Mining Industry, 2015, 7(9): 99−103.
[16] GAO Song, LI Bin. Study on slurry noise of electromagnetic flowmeter based on ARMA power spectrum estimation[J]. Mathematical Problems in Engineering, 2013, 715(1): 1856−1862.
[17] YIN Shiyi, LI Bin. Research on direct calibration of electromagnetic flowmeter in partially filled pipes[J]. Advanced Materials Research, 2013, 712(3): 1904−1909.
[18] MICHALSKI A, JAKUBOWSKI J, WATRAL Z. The problems of pulse excitation in electromagnetic flowmeters[J]. IEEE Instrumentation and Measurement Magazine, 2013, 16(5): 47−52.
[19] CAO Zhang, SONG Wei, PENG Zhicong, et al. Coil shape optimization of the electromagnetic flowmeter for different flow profiles[J]. Flow Measurement and Instrumentation, 2014, 40(1): 256−262.
(编辑 罗金花)
Optimization of electromagnetic flowmeter excitation coil
ZHANG Hao, YUE Shihong, ZHANG Yujing, WANG Huaxiang
(School of Electrical Engineering and Automation, Tianjin University, Tianjin 100072, China)
Magnetic field induced by different shapes of excitation coil was simulated from the angle of the weighting function, three indicators, the magnetic flux density along the central axis of the distribution of evenness, along the measuring tube axis of the distribution uniformity and the uniformity of the distribution in the whole space were defined to analyse their magnetic field uniformity respectively, and then the optimal coil shape was chosen. And in the situation of the same coil material cost and the same excitation condition, the relationship between EMF induced by different shape coils and the measured liquid velocity and the level of liquid in the pipe was simulated. The results show that the circular coil magnetic field uniformity is the best. The selection of the best shape of the exciting coil has been done based on the measured liquid level in the pipe line in practical application.
electromagnetic flowmeter; magnetic field homogeneity; optimization of excitation coil; magnetic field intensity; weighting function
10.11817/j.issn.1672-7207.2016.06.018
TH814
A
1672−7207(2016)06−1953−06
2015−06−13;
2015−08−20
国家自然科学基金资助项目(61774014,61573251);国家国际科技合作专项资助项目(2013DFA11040)(Projects(61774014, 61573251) supported by the National Natural Science Foundation of China; Project(2013DFA11040) supported by International S&T Cooperation Program of China)
岳士弘,教授,从事电学层析成像、电磁流量计研究;E-mail:shyue1999@tju.edu.cn

