钢包钙处理工艺中钙汽化过程的数值模拟
王顺玺,张炯明,宋炜,王博,白敦敏
钢包钙处理工艺中钙汽化过程的数值模拟
王顺玺,张炯明,宋炜,王博,白敦敏
(北京科技大学钢铁冶金新技术国家重点实验室,北京,100083)
根据钙处理过程中汽化速率的变化特点,结合实际喂线工艺参数,将钙处理工艺分为喂线阶段和弱搅静置2个阶段,建立钢包钙汽化过程的数学模型。利用大型商业软件CFX,模拟钙的汽化过程,并研究不同喂线速率对钙收得率的影响。研究结果表明:喂线阶段与弱搅静置阶段钙的实际汽化速率有较大差异;当喂线阶段实际汽化速率与理论气泡上浮速率之间的比例系数=0.4、弱搅阶段表观速率常数e=0.001 2 s−1时,模拟计算的钙质量分数与实验钙质量分数较吻合,从而确立适合模拟的基础参数;当喂线速度为200 m/min时,喂线180s后,钙在钢中分布极不均匀,经过弱搅静置阶段,即喂1 000s后,钢液中钙质量分数均匀分布,平均质量分数为1.86×10−5,钙的收得率为23.2%;随着喂线速率的增加,喂线深度随之增加,钙的汽化量减小,收得率增加。
钙处理;钙汽化;钙收得率;数值模拟
近年来,通过钙处理工艺来改善铝镇静钢水口堵塞,以提高钢产品的质量已成为一种常用的手段。钙的收得率是衡量钙处理效果的重要指标[1−2]。然而,在实际喂钙的过程中伴随着剧烈的钙汽化反应,该反应影响钢液的钙收得率,导致钙处理效果往往较差,为此,众多研究人员进行了大量的基础研究和实践探索,主要涉及钙反应的热力学[3−7]、夹杂物的析出和衍 变[8−11]、变性与去除[12−15]、反应过程数值模拟[16−17]等,但针对钙的汽化过程模拟、钙的收得率研究较少。钙的沸点较低,在钢中钙的汽化反应特点与金属镁有相似之处,MACHLIN[18]提出了钢液中的镁汽化速率的计算公式,IRONS等[19]研究了在搅拌情况下金属镁的汽化,所测得的钙、镁此类低沸点金属在钢中的汽化速率与MACHLIN[18]所计算的结果较接近,验证了沸点较低的金属在钢液中的汽化速率计算公式的正确性。HIGUCHI等[20]在IRONS等[19]研究的基础上建立了钙处理过程中夹杂物变性的数学模型,该模型考虑了钙的汽化及夹杂物与钢液物质的反应。LU[21]通过实验研究了钙处理中钙的汽化对钙收得率的影响,揭示了钙与钢中氧、硫的反应机理,建立了钙与夹杂物反应的动力学模型。BASAK等[22]通过量纲分析得出在200 m/min的喂线速度时,钙的收得率最大,并且与量纲一的参数毕渥数、量纲一的熔池温度等有对应的线性关系。魏军[23]通过热力学计算,建立了喂钙量预报模型,但是没有考虑动力学的影响。吴苏州[24]应用未反应核模型研究了钙处理动力学机理,假设钙在钢中的传质为限制行环节,得出钢液中钙质量分数越大,对钙处理的动力学效果越明显。然而,上述研究均未考虑钙处理过程中喂线阶段和弱搅拌阶段不同的钙汽化速率。为此,本文作者在前人研究的基础上,针对钙处理工艺中不同阶段采用不同的汽化速率计算式,建立模型并进行数值模拟,研究钙的汽化过程的影响因素,旨在为精确控制钙的收得率提供参考。
1 研究方法及内容
以某厂的X70管线钢为研究对象,实际生产工艺流程为铁水预处理、转炉、LF炉精炼、RH精炼、中间包、连铸,其所冶炼钢种的化学成分如表1所示。其中在RH精炼结束前,以200 m/min的喂线速率向钢液中喂入600 m硅钙线,采用的硅钙线直径为 13 mm,钢带厚度为0.35 mm,钢带密度为230 g/m,钙的质量分数为0.287,喂线时间约为3 min。喂线后根据生产节奏静置8~15 min后进行浇注。钢包及喂线参数如表2所示。

表1 冶炼钢种的化学成分(质量分数)

表2 钢包及喂线参数
取5个炉次作为实验对象,分别在喂线前、喂线后1,5和11 min取样分析钢样的钙成分变化,如表3所示。从喂线前钢中钙元素质量分数结果可以看出:钢中的钙质量分数为(1~6)×10−6,钙质量分数较低,所以,在本文模拟中忽略喂线前钢中的钙质量分数,近似认为钢中的初始钙质量分数为0。
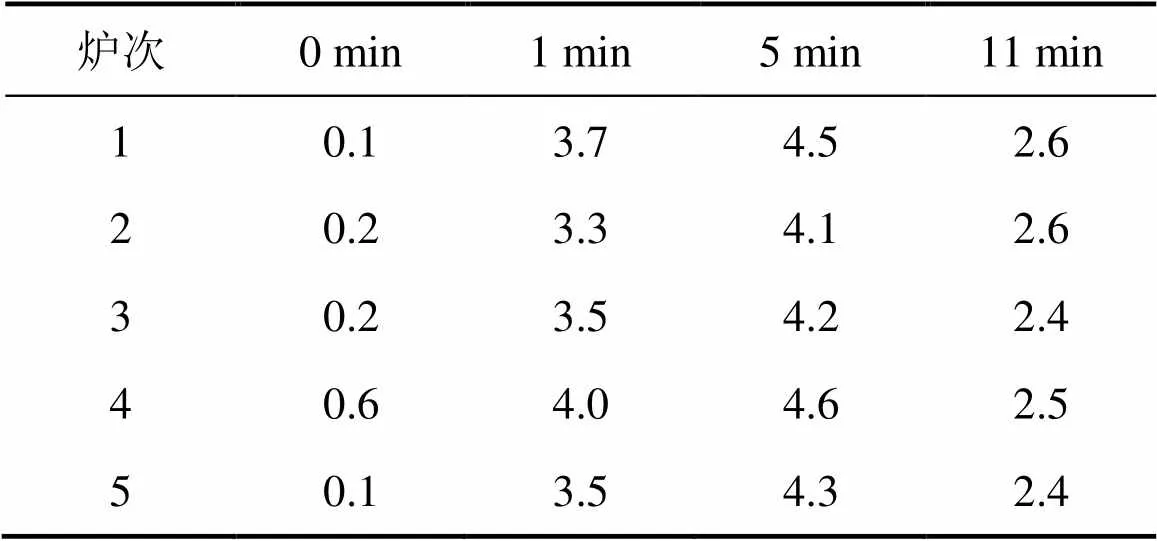
表3 喂线后不同时刻钢中钙元素质量分数
从表3可以看出:钢中的钙质量分数首先随着喂线时间增加而增加,当喂线结束后钢中的钙质量分数达到最大值,之后随着时间的增加,钢中的钙质量分数减小。钙质量分数减小的主要原因是钙的汽化。在喂线初期钙不断加入钢中,造成钙的大量汽化,且汽化速率较大。喂线开始时刻为初始时刻,3 min后喂线结束,5 min时钢中的钙的平均质量分数仅为4.3×10−5,相对于喂入的总钙线量,实际进入钢液的钙非常少,说明喂线过程中钙的汽化速率很大;在11 min处于弱搅阶段总钙的平均质量分数为2.6×10−5,此阶段钢中钙的质量分数变化并未发生剧烈波动,可以看出弱搅阶段钙的汽化速率较小。
2 钢包喂钙过程的数学模型
数学模型的建立基于2个层次:首先对钢包中的钢液和底吹氩气建立钢包汽液两相的流动数学模型;然后假设钙的汽化和钙在钢液中的传质对钢液的速度场无影响,将流场赋值于喂钙过程汽化模型中,计算钙在钢液中的质量分数变化。
2.1 钢包流动的数学模型
2.1.1 基本假设
由于实际生产过程极其复杂,数学模型尚且无法做到十分精确,因此,需对钙处理喂线过程进行如下假设:1) 钢液视为不可压缩的牛顿流体;2) 氩气泡粒径均匀,气泡间不发生碰撞聚合或单一气泡破碎;3) 不考虑钢液面波动及喂线对流场的影响;4) 气液两相间相互运动仅靠密度差驱动,相间界面力仅为拖曳力;5) 忽略渣层。
2.1.2 基本方程
1) 连续性方程:
式中:φ和φ分别为和的体积分数,φ+φ=1;相为钢液;相为氩气泡;ρ和ρ分别为和的密度,kg/m3;和分别为和的速度矢量,m/s。
2) 动量守恒方程:
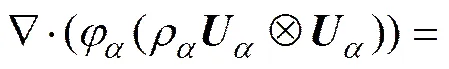
式中:为系统压强,Pa;μeffμeff分别为和相的有效黏度,kg/(m∙s);M为相作用于相的界面力,M为相作用于相的界面力,且满足M=−M。
3) 对于钢液连续相,有效湍流黏度公式为
式中:μ为相的有效湍流黏度,Pa∙s;C为湍流模型常数,0.09;ρ为相的指令平均密度,kg/m3;k为相的湍动能,m−2·s−2;ε为相的湍动能耗散,m−2·s−3。
流场的模拟参数及物质的物理参数如表4所示。

表4 模拟参数及物质的物理参数
钢液上表面定义为气体脱离出口,钢液视此为壁面,且为自由滑动条件,钢液在此处的速度梯度和壁面对钢液的剪切力为0 Pa,则钢包顶面边界条件如下。
对钢液,
对氩气,
式中:l,l和l分别为,和方向的钢液速度,m/s;g,g和g分别为,和方向的氩气速度,m/s。
对于湍流流动,由于近壁处动量波动迅速减弱,故需考虑到湍流作用的减弱和层流作用的相对增强,此处由壁面函数指定其行为,钢液与氩气在壁面处均为无滑移条件,则壁面的边界条件为
钢包底吹氩孔为入口边界。
2.2 钙喂过程的汽化模型
2.2.1 基本假设
1) 实际生产中硅钙线钙质量分数一般为20%~30%。此模型中直接将硅钙线中的钙折算为纯钙,以相同的喂线速率喂入钢中。
2) 喂入的钙以游离钙形式溶解于钢液中,且初始时刻钢中的钙质量分数为0。
3) 忽略表层渣及钢渣间反应,忽略渣层对钢中钙质量分数的影响,认为钢中的总钙质量分数的减少由汽化造成。
2.2.2 基本理论
由于钙的沸点较低,在炼钢温度下极易汽化,造成喂钙过程中钙的收得率很低。喂钙过程中钙在钢液中的汽化过程十分复杂,因而研究其汽化速率较困难。钢中钙的汽化反应特点与金属镁有相似之处,MACHLIN[18]提出了镁的汽化速率计算公式:
式中:为熔池深度,m;Mg为镁的传质系数,m/s;(Mg)为Mg在钢液中的质量分数。
IRONS等[19]通过向有搅拌条件下的钢液中通入镁气,测定镁在钢液中的汽化速率,验证了镁此类沸点较低的金属在钢液中的汽化速率计算公式的正确性。在有强搅拌的情况下,有
式中:K为物质的传质系数,m/s;为物质到钢液面的平均速度,m/s。
OHNO[25]研究了合金元素在液态金属中的汽化过程,提出物质向液态金属界面扩散速率方程为
式中:为金属液体的表面积,m2;为金属液体的体积,m3;ω为物质的质量分数。
HIGUCHI等[20]在研究钙处理变性夹杂物数学模型时,考虑了钙的汽化及夹杂物与钢液物质的反应,其在计算钙的汽化速率时采用
式中:Ca为钙的传质系数,m/s;为钢液的体积,m3。钢中钙质量分数的实验测定值与其模型计算值基本吻合。
在实际钙处理工艺中,底吹氩气弱搅拌贯穿于整个操作过程。在喂线阶段,钙的汽化速率非常大,钢液中会形成大量的钙气泡及白烟,所以引入钙气泡直径g来建立模型;喂线操作完成后,为保证钢液成分均匀,继续底吹氩气弱搅拌,此时,钙的汽化速率小于喂线时钙的汽化速率。在研究钙汽化时,根据实际工艺将喂钙分为2个阶段来讨论,即为钙汽化较剧烈的喂线阶段和弱搅阶段。
1) 喂线阶段模型建立。在实际情况下,钢中喂入钙,部分钙要溶解,还有部分钙要与钢中的物质发生反应,其他的钙发生汽化反应变为钙气泡脱离钢液,造成实际喂入的钙形成的气泡小于理论计算值,所以,钙气泡的理论上浮速率并不等于钙的实际汽化速率。钙的实际汽化速率小于钙气泡的理论上浮速率,并与其呈正比关系,设置比例系数为。综合强搅拌情况下适用的式(8)和式(9),喂线阶段由气泡上浮造成的钙质量分数的损失为
式中:为比例系数;为钢液深度,m。
唐海燕等[26]在研究钢液钙处理的动力学时发现钙粒的粒径s对汽化形成的气泡在钢液中上浮速度g影响较大。假设喂入的钙线以直径为s的小颗粒进入钢液,则钙颗粒形成气泡的直径表达式为
式中:s为钙的密度,kg/m3;Ca为钙的摩尔质量;kg/mol;m为钢液的密度,kg/m3;θ为标准大气压,0.101 MPa;为钙所处钢液深度,m。
根据文献[27],气泡上浮速度g为
得气泡上浮速度为
由此可知,气泡的上浮速率与初始钙粒的粒径、钢液的温度、喂入深度有关。所以结合式(12)和式(15),喂线阶段钙在钢中钙的变化可以表示为

(16)
2) 弱搅静置阶段模型建立。当喂线结束后,钢包中钙的汽化不再剧烈,所引起的搅动也不如喂线期剧烈,钙的汽化速率会减小,所以,此阶段采用文献[20]中的汽化速率表达式,即钙汽化速率的限制环节为钙在钢中的传质,钢中钙的质量分数变化可表示为
式中:m为传质系数,m/s;e为表观速率常数,s−1。由式(17)可以看出:e为钙汽化过程的重要参数,直接影响钢中钙的质量分数及钙的收得率。
钢液中钙元素的质量分数变化为
式中:Гeff为有效扩散系数,kg∙m−1∙s−1;w为物质的质量分数;U钢液性,和方向上的质量平均速度,m/s;S为物质反应的源项;x为坐标系,和。
此模型中喂线阶段钙汽化源项ie1由式(19)给出,弱搅阶段的源项ie2由式(20)给出:

(19)
式中:ie为钙的汽化源项。
2.2.3 喂线深度
实际喂钙线过程中喂线深度是由喂线速率来控制的,本模型中的喂线深度由工业喂硅钙线速度Ca-Si确定:
式中:Ca-Si为硅钙线的喂线速度,m/s;为钢包钢水深度,m;为包芯线熔化时间,s;−为钢包内硅钙线的插入深度,m;为修正系数,为1.5~2.5。
采用硅钙线钙的质量分数为0.287,据该硅钙线得出[28]在1 873 K下,熔化时间为1.26 s。根据实际情况,本文中取1.85,则得=1.44 m,从而得出喂线速度为200 m/min时喂线深度为2.27 m。
2.3 计算方法
基于CFX大型商业软件,对喂线线过程中钢液的流动、钙的汽化等过程进行数值模拟,整个模拟过程有以下几步:
1) 生成物理模型。根据实际模型尺寸进行建模。
2) 网格划分。物理模型建立后,进行六面体网格划分。
3) 模型建立。对钢包流场,钙的汽化以及反应等情况进行设定,并生成运算文件。
4) 求解。对步骤3)中生成的运算文件进行求解,求解方法为有限体积法,收敛残差小于10−4。
3 结果与讨论
3.1 流场模拟结果分析
流场计算结果如图1所示。从图1可以看出:底吹氩气在浮力作用下向上运动,带动钢液向上运动,射流区的钢液的速度始终向上,随着气流上升钢液的速度逐渐增大;同时,由于流股内的压力的减小,会不断吸入周围的钢液,气−液两相流区面积随着高度的增加而增大,从而起到搅拌混匀钢液的作用;当气−液两相流区的流线到达钢包顶部时,氩气逸出熔池,而钢液以较大的速度流向周围钢包壁。本文采用的是双孔底吹氩气,2股气−液两相流区之间的钢液处交汇,从而形成2个较大的漩涡。在钢包两侧由于钢包壁阻挡,钢液沿着钢包壁向下流动,形成2个较小的漩涡,然后在气−液两相流区的作用下,再次循环形成回流。

(a) 钢包横截面钢液速度矢量图;(b) 纵截面处速度矢量图;(c) 钢包内纵截面流线图
3.2 喂线阶段的比例系数及弱搅阶段e的确定
设定钙颗粒直径s=1 mm[26],根据实际工艺中钢中钙质量分数的变化,来确定喂线阶段实际汽化速率与理论气泡上浮速率之间的比例系数、弱搅阶段的表观速率常数e。文献[20]在计算钙的汽化时,采用m=0.007 5 m/s,最终其模型计算结果与实验室试验的测定值基本吻合。在实际生产中汽化速率与实验室试验不同,无法确定钙的汽化速率,因此,本文以文献[20]中的m=0.007 5 m/s,e=0.002 19 s−1为基础,按照实际工艺过程中钙的收得率,来确定弱搅阶段钙的汽化速率。依据式(18)为基础经过多次计算与调整,计算流程如图2所示。

图2 计算流程
计算出钙的变化曲线如图3所示。从图3可以看出:喂线阶段由于钙的不断喂入,钢中钙的增加速率大于钙的汽化速率,钢中钙质量分数不断增大;当喂线结束时,钢中的钙质量分数达到最大值,随后在弱搅阶段,钢中的钙质量分数一直减小。汽化模型计算值与实际值较为吻合,此模型可以用于该厂生产工艺情况下的模拟计算。最终确定喂线阶段实际汽化速率与理论气泡上浮速率之间的比例系数0.4,弱搅阶段表观速率常数e=0.001 2 s−1,模拟计算钢中钙质量分数与实际过程中的钙质量分数较吻合。

图3 计算数据与实际数据的对比
据钢包纵截面,可从整体上直观地分析钢包内部钙的质量分数分布。本模型中钢包是以面对称的,以对称面作为纵截面观察对象。同时在钢包模型内选取6个点,分别监测这6个点上的钙质量分数分布情况,纵截面和监测点位置如图4所示。

图4 钢包监测点示意图
图5所示为钢包纵截面喂线后钙质量分数在钢中的分布云图及变化情况。从图5可以看出:喂线以后在流场的作用下,钙在钢液中向钢包上方扩散,同时在钙质量分数梯度的作用下向周围扩散,扩散的同时钙以一定的速率汽化;在0~20 s内,钙只分布在钙线周围,180 s后喂线结束,钙质量分数在钢中分布极不均匀,直到1 000 s左右钙均匀地分布于钢液中。

喂线时间/s:(a) 1;(b) 5;(c) 20;(d) 100;(e) 180;(f) 400;(g) 600;(h) 1 000
钢包6个不同位置的监测点的钙质量分数变化如图6所示。由图6可以看出:喂线后钙在12 s后最先到达点1,在190 s时钙质量分数达最大值4.57×10−4;在30 s左右到达点5,在220 s左右达最大值 3.44×10−4;50 s左右到达点2,在262 s左右到达最大值1.28×10−4。

1—点1;2—点2;3—点3;4—点4;5—点5;6—点6。
钙分别在105 s左右到达点4,在126 s左右到达点3,170 s左右到达点6。结合图5所示钙的质量分数分布云图,分析钙的扩散规律是先随着流场向上扩散达到钢包顶部,又向下扩散。所以钢包下方的点3、点4、点6钙到达得较慢。由于点6处于死区位置,钢液的活动较小,所以,到达点6的耗时最长。
180 s后喂线结束,钙质量分数在6个监测点的分布相差很大,此时继续对钢包底吹氩气弱搅拌,直到1 000 s左右钙均匀分布于钢液中,此时钢中的钙质量分数为1.86×10−5。模拟结果表明喂线后弱搅阶段对于均匀钢液中钙质量分数有非常重要的作用。
3.3 不同喂线速率对钙收得率的影响
为了研究不同喂线速率对钙汽化和钙收得率的影响,模型中设定喂线速率分别为50,100,150,200和250 m/min。由于喂线速率的变化,喂线量不变,由式(21)计算得出喂线深度与喂线时间也相应发生变化,表5所示为5种不同喂线速率工况。

表5 不同喂线工况
图7所示为在不同喂线速率条件下钢中钙平均质量分数随时间的变化曲线。从图7可见:随着喂线的进行,钢中的钙质量分数不断地增大,但增加趋势不断减小。这是由于在喂线初始阶段,钙的质量分数较小,所以,钙的汽化量较小;喂入钢液的钙量比汽化损失的钙量大得多,所以,喂线开始阶段钙质量分数增加速率较大;随着喂线的进行,钙质量分数逐渐增加,但钙质量分数的增加同时造成钙的汽化量增大,所以钙的增加速率减小,钙质量分数曲线趋于平缓;当喂线结束时,钢中钙质量分数达到最大值。
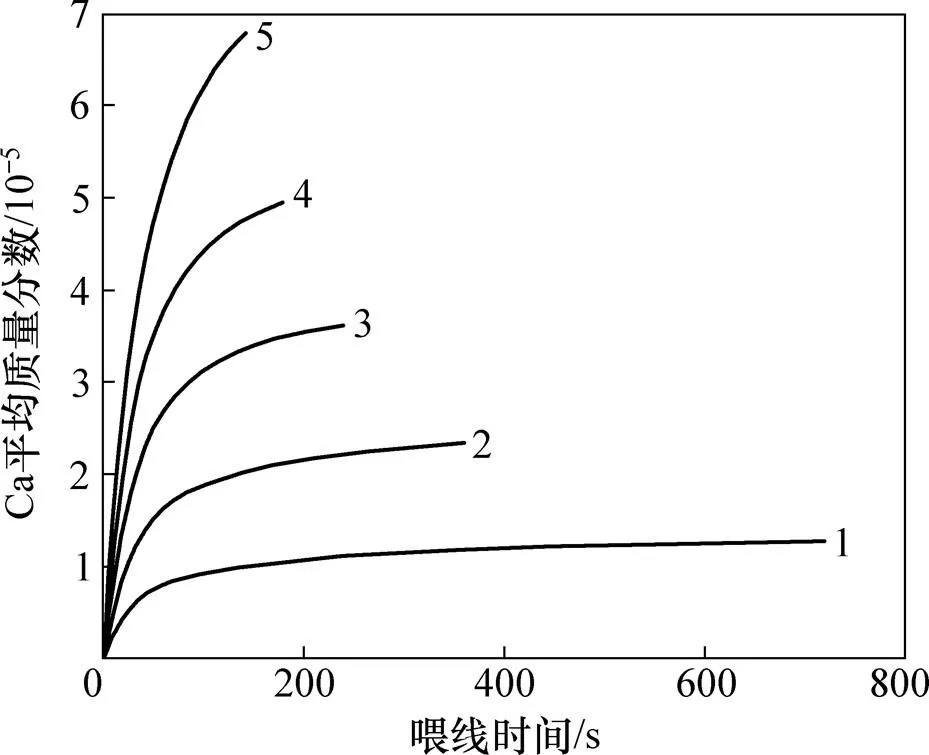
喂线速率/(m∙min−1):1—50;2—100;3—150;4—200;5—250。
当喂线速率为50 m/min时,喂线深度较浅,钢液的静压力较小,造成喂入钢液的钙极容易形成气泡,且形成的气泡较大,上浮速率较快,使钙的汽化较快,当喂线结束时,钢中的钙平均质量分数达最大值 1.29×10−5;对于喂线速率为100,150,200和 250 m/min的情况,随着喂线速率的增加,喂线深度和钢液的静压力随之增加,不容易形成钙气泡,使钙的汽化速率减小;当喂线结束时,钢中钙质量分数分别为2.36×10−5,3.65×10−5,4.99×10−5和6.85×10−5。
忽略渣层对钙质量分数的影响,认为除了汽化的钙,其他钙量均进入钢液。钙收得率即为钢液中的钙量与喂钙量的比值。图8所示为喂线速率与钙的收得率关系图。由图8可得:钙的收得率与喂线速率几乎呈线性关系,可见在一定范围内,随着喂线速率的增加,钙收得率增加。
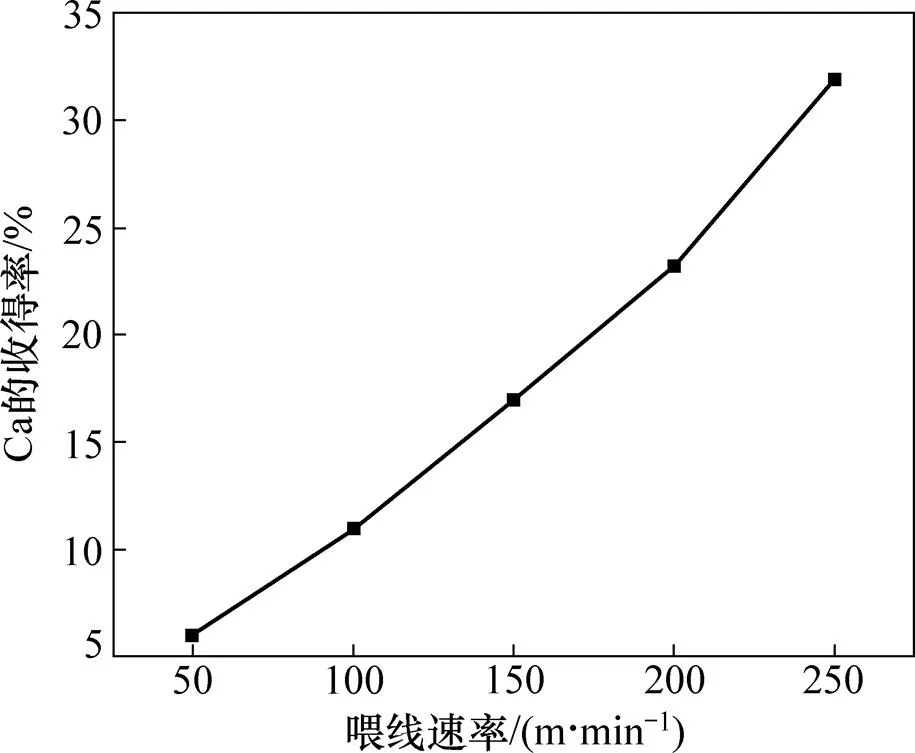
图8 喂线速率与收得率的关系
4 结论
1) 现场取样分析得出喂线结束后钢中的平均钙质量分数仅为4.3×10−5,说明在实际喂线过程中钙的汽化速率很大;在喂线结束后11 min时,处于弱搅阶段总钙的平均质量分数为2.6×10−5,可以看出弱搅阶段钙的汽化速率较小。
2) 依据实际工艺,基于不同的2个阶段即钙汽化较剧烈的喂线阶段和弱搅阶段,进行数值模拟,最终确定喂线阶段汽化速率与气泡上浮速率之间的比例系数=0.4,弱搅阶段表观速率常数e=0.001 2 s−1,模拟计算钢中钙质量分数与实际过程中的钙质量分数较吻合。
3) 通过分析钢中钙的质量分数及分布,发现喂入钙开始后,钙在钢液流场作用下向钢包上方扩散,同时在钙浓度梯度的作用下向周围扩散。在喂线阶段,钙最先到达钢液上表面,随后经过弱搅阶段,钢液成分逐渐均匀,到达钢包底部,在1 000 s左右钙完全均匀分布于钢中,钙平均质量分数为1.86×10−5,收得率为23.2%。
4) 计算不同喂线速率下钙的收得率发现,随着喂线速率的增加,喂线深度也在增加,钙的汽化量减小。在一定范围内,随着喂线速率的增加,喂线结束后钢中钙质量分数随之增大,钙收得率增加。
[1] DENG Zhiyin, ZHU Miaoyong, ZHONG Baojun, et al. Attachment of liquid calcium aluminate inclusions on inner wall of submerged entry nozzle during continuous casting of calcium-treated steel[J]. Journal of Iron and Steel Research, International, 2014, 54(12): 2813−2820.
[2] MANABU T. Sheet steel technology for the last 100 years: progress in sheet steels in hand with the automotive industry[J]. Journal of Iron and Steel Research, International, 2015, 55(1): 79−88.
[3] CHOUDHARY S K, GHOSHA G. Thermodynamic evaluation of formation of oxide-sulfide duplex inclusions in steel[J]. Journal of Iron and Steel Research, International, 2008, 48(11): 1552−1559.
[4] GHOSH A. Calcium treatment of liquid steel: assessment of deoxidation constant[J]. Transactions of the Indian Institute of Metals, 2008, 61(6): 473−475.
[5] TAGUCHI K, ONO−NAKAZATO H, NAKAI D, et al. Deoxidation and desulfurization equilibria of liquid iron by calcium[J]. Journal of Iron and Steel Research, International, 2003, 43(11): 1705−1709.
[6] SUN Guodong, SUI Yafei, WANG Canguo. Thermodynamic calculation on calcium treatment for 26CrMo4S2steel[J]. Journal of Iron and Steel Research, International, 2014, 21(Suppl 1): 61−64.
[7] ZHANG Feng, MIAO Lede, ZONG Zhenyu, et al. Effects of calcium treatment on non-metallic inclusions and magnetic properties of non-oriented silicon steel sheets[J]. Bao Steel Technical Research, 2013(1): 12−19.
[8] 隋亚飞, 孙国栋, 王灿国, 等. 石油钻杆钢冶炼过程中夹杂物的析出和衍变[J]. 北京科技大学学报, 2014, 36(11): 1462−1470. SUI Yafei, SUN Guodong, WANG Canguo, et al. Inclusion formation and evolution in steelmaking process for drill pipes[J]. Journal of University of Science and Technology Beijing, 2014, 36(11): 1462−1470.
[9] YANG Guangwei, WANG Xinhua. Inclusion evolution after calcium addition in low carbon Al-killed steel with ultra low sulfur content[J]. Journal of Iron and Steel Research, International, 2015, 55(1): 126−133.
[10] YANG Wen, ZHANG Lifeng, WANG Xinhua, et al. Characteristics of inclusions in low carbon Al-killed steel during ladle furnace refining and calcium treatment[J]. Journal of Iron and Steel Research, International, 2013, 53(8): 1401−1410.
[11] LIU Jianhua, WU Huajie, BAO Yanping, et al. Inclusion variations and calcium treatment optimization in pipeline steel production[J]. International Journal of Minerals, Metallurgy, and Materials, 2011, 18(5): 527−534.
[12] JUNG−HWAN S, IN−HO J, SUNG−MO J, et al. Chemical reaction of glazed refractory with Al-deoxidized and Ca-treated molten steel[J]. Journal of Iron and Steel Research, International, 2010, 50(10): 1422−1430.
[13] TSHILOMBO K. Determination of inclusions in liquid steel after calcium treatment[J]. International Journal of Minerals, Metallurgy, and Materials, 2010, 17(1): 28−31.
[14] YANG Shufeng, LI Jingshe, WANG Zaifeng, et al. Modification of MgO·Al2O3spinel inclusions in Al-killed steel by Ca-treatment[J]. International Journal of Minerals, Metallurgy, and Materials, 2011, 18(1): 18−23.
[15] REN Ying, ZHANG Lifeng, LI Shusen. Transient evolution of inclusions during calcium modification in line pipe steels[J]. Journal of Iron and Steel Research, International, 2014, 54(12): 2772−2779.
[16] SANYAL S, CHANDRA S, KUMAR S, et al. An improved model of cored wire injection in steel melts[J]. Journal of Iron and Steel Research, International, 2004, 44(7): 1157−1166.
[17] VERMA N, PISTORIUS P C, FRUEHAN R J, et al. Calcium modification of spinel inclusions in aluminum-killed steel: reaction steps[J]. Metallurgical and Materials Transactions B, 2012, 43(4): 830−840.
[18] MACHLIN E S. Kinetics of vacuum induction refining theory[J]. Trans TMS-ATME, 1960, 218: 314−326.
[19] IRONS G A, CHANG C W, GUTHRIE R I L, et al. The measurement and prediction of the vaporization of magnesium from an inductively stirred melt[J]. Metallurgical Transactions B, 1978, 9(2): 151−154.
[20] HIGUCHI Y, MUMATA M, FUKAGAWA S, et al. Inclusion modification by calcium treatment[J]. The Iron and Steel Institute of Japan, International, 1996, 36(1): 151−154.
[21] LU D Z. Calculation of CaS and MnS activities and their application to calcium treatment of steel[J]. Ironmaking & Steelmaking, 1991(5): 342−346.
[22] BASAK S, KUMAR D R, ROY G G. Efficacy and recovery of calcium during Ca-Si cored wire injection in steel melts[J]. Ironmaking & Steelmaking, 2010, 37(3): 161−168.
[23] 魏军. BOF-LF-CSP 流程低碳铝镇静钢非金属夹杂物行为研究[D]. 北京: 北京科技大学冶金与生态工程学院, 2005: 45−47. WEI Jun. Study on the behavior of non-metallic inclusions of low carbon Al-killed steel in BOF-LF-CSP process[D].Beijing: University of Science and Technology Beijing. School of Metallurgical and Ecological Engineering, 2005: 45−47.
[24] 吴苏州. 浸入式水口堵塞过程动力学及电磁控制的研究[D]. 北京: 北京科技大学冶金与生态工程学院, 2010: 83−84. WU Suzhou. Study of kinetics of submerged entry nozzles clogging and electromagnetic control[D]. Beijing: University of Science and Technology Beijing. School of Metallurgical and Ecological Engineering, 2010: 83−84.
[25] OHNO R. Rates of evaporation of silver, lead, and bismuth from copper alloys in vacuum induction melting[J]. Metallurgical Transactions B, 1976, 7(4): 647−653.
[26] 唐海燕, 李京社, 郭汉杰. 钢液钙处理脱氧脱硫的动力学[J]. 北京科技大学学报, 2009, 31(6): 690−695. TANG Haiyan, LI Jingshe, GUO Hanjie. Deoxidation and desulfurization dynamics of molten steel with calcium treatment[J]. Journal of University of Science and Technology Beijing, 2009, 31(6): 690−695.
[27] 郭汉杰. 冶金物理化学教程[M]. 北京: 冶金工业出版社, 2006: 130. GUO Hanjie. Metallurgical physical chemistry course[M]. Beijing: Metallurgical Industry Press, 2006: 130.
[28] 刘丹妹. 湘钢E级船板钢质量和钢包喂钙硅线模型的研究[D]. 北京: 北京科技大学冶金与生态工程学院, 2007: 69−70. LIU Danmei. Research on the quality of E grade hull structural steel and the model of Ca-Si wire addition in ladle[D]. Beijing: University of Science and Technology Beijing. School of Metallurgical and Ecological Engineering, 2007: 69−70.
(编辑 刘锦伟)
Numerical simulation of calcium vaporization during Ca-treatment process in ladle
WANG Shunxi, ZHANG Jiongming, SONG Wei, WANG Bo, BAI Dunmin
(State Key Laboratory of Advanced Metallurgy, University of Science and Technology Beijing, Beijing 100083, China)
According to the law of calcium vaporization change in calcium treatment and actual data feeding wire process, the vaporization of calcium model was established based on two different calcium vaporization stages, feed wire period and week stirring period. The changing rules of calcium recovery with different feedrates were simulated through CFX. The results show that there are apparently different vaporization velocities between feed wire period and week stirring period. Actual vaporization velocity is proportional to theoretical floatation velocity of calcium bubble. When the proportional coefficientis 0.4 in the feeding wire process and the apparent rate constanteis 0.001 2 s−1 in weak stirring stage, this numerical simulation matches actual plant data very well. At 200 m/min of feeding wire rate, the distribution of the mass concentration of calcium is uneven at 180 s after the end of feed wire. However, the calcium distributes equally in melt after week stirring period. The average mass fraction of calcium is 1.86×10−5and the recovery of calcium is 23.2%. At some extent, the deepness of feeding wire and the calcium recovery increase with the feeding rate, whereas the vaporization of calcium may increase.
calcium treatment; calcium vaporization; recovery of calcium; numerical simulation
10.11817/j.issn.1672-7207.2016.06.005
A
1672−7207(2016)06−1850−10
2015−06−05;
2015−08−30
国家自然科学基金资助项目(51474023); 国家高技术研究发展计划(863计划)项目(2012AA03A505)(Project(51474023) supported by the National Natural Science Foundation of China; Project(2012AA03A505) supported by the National High-Tech Research & Development Program (863 Program) of China)
张炯明,博士,教授,从事连铸工艺技术、凝固理论、冶金反应工程和计算机数值模拟等研究;E-mail:jmz2203@sina.com

