产品二维不完全预防性维修间隔期优化研究

韩玉成，贾希胜，白永生，李欣玥

（军械工程学院装备指挥与管理系，河北石家庄050003）

产品二维不完全预防性维修间隔期优化研究

韩玉成，贾希胜，白永生，李欣玥

（军械工程学院装备指挥与管理系，河北石家庄050003）

针对故障受日历时间与使用时间共同影响的二维产品，传统的一维预防性维修已不能满足二维产品的实际需求，鉴于此，提出二维预防性维修概念，以日历时间与使用时间对二维产品进行二维预防性维修决策。建立二维产品故障率函数表达式，对二维预防性维修的过程进行具体的分析，以总期望费用最小为优化目标，建立有限使用期二维不完全预防性维修费用模型。通过实例求出最佳的二维不完全预防性维修间隔期，经对比分析验证了该模型的适用性与有效性，对二维维修策略提出了展望。

兵器科学与技术；二维不完全预防性维修；数学模型；虚拟工龄

0 引言

由于社会的不断进步与经济的快速发展，产品性能越来越先进，复杂性越来越高，很多复杂产品的寿命受产品的日历时间、使用时间、固有可靠性等因素的共同影响。过久的使用时间或过高使用强度将加速产品部件的退化、增加产品的故障强度。陈相侄［1］对二维产品保证的概念进行了阐述，其中二维产品的故障就受日历时间与使用时间的共同影响，使用时间可以是打印机的打印张数，汽车的行驶里程，飞机的起降次数等。对此类产品进行预防性维修时，不仅要按照传统的做法给出单一的日历时间间隔期，还要结合实际的使用情况，确定反映使用情况的使用间隔期。比如说在工业领域，家用汽车的维护保养，多采用日历时间与行驶里程的二维约束，通常间隔期为半年或者10 000 km，在消费者正常的使用情况下，无论哪个期限先到，就进行相应的维护保养。

国外关于二维产品维修的研究最初来源于产品的保修领域，目前关于二维保修的研究主要是关于二维保修策略以及成本的优化研究，以保修期内费用最低为决策目标，确定二维保修期限内最优的维修策略。Iskandar等［2］针对可修产品，提出产品故障在特定的保修期范围内采取更换措施，其余时间内采用最小维修的策略，以降低保修期内保修成本；Chukova等［3］对二维产品保修开展了最优维修策略的研究，其将可修产品的保修期划分为3个不相交的区域，对每个特定的区域设置一个预定的维修策略，通过确定区域边界降低产品的保修成本；Jack等［4］、Varnosafaderani等［5］、Chen等［6］也都对二维保修期内发生故障后的维修策略进行了优化。可以发现大部分二维保修的文献都是针对故障后维修的情况，在二维保修期内采用预防性维修的策略相对较少。

有关预防性维修已经开展了大量研究，预防性维修是为预防产品故障或故障的严重后果，使其保持在规定状态所进行的全部活动［7］。Yeh等［8］在故障率增加的定期更换策略下，得到了最小的长期期望费用，得出了最优更换间隔期在保修期结束后应调整的结论；Shahanaghi等［9］在二维保修期下，采用定期不完全预防性维修的策略，建立了关于费用的模型，以费用最小为决策目标，对预防性维修的次数以及维修程度进行了优化；Hu等［10］考虑了二维预防性维修的问题，提出了一个以日历时间与使用时间同时进行备件更换的二维预防性维修策略，最终对备件需求量进行了优化求解。

通过以上综述可以发现，传统的二维保修是在二维的约束下（即二维保修期内）开展一系列的维修策略优化研究，维修策略优化的时间变量都是日历时间（即传统的一维维修），很少有文章考虑到二维预防性维修的问题。不完全维修又是预防性维修中最为普遍的方式，所以对于可以准确获取到日历时间与使用时间的产品，以费用为优化目标，对其二维预防性维修间隔期进行优化研究具有重要的现实意义。本文旨在确定最优的一组日历时间与使用时间（T0，U0）使总期望费用最低，即无论产品的哪个时间先到达给定的阈值，就开展相应的预防性维修活动。

因此，本文结合产品的使用与维修实际，从二维产品预防性维修的角度出发，研究二维产品在有限使用期下二维不完全预防性维修间隔期的确定问题。

1 模型描述、假设与参数

1.1模型描述

主要针对寿命受日历时间T与使用时间U双重影响的批次产品，为了降低产品的维修费用，同时为了提高产品的完好性，对批次产品采取定期不完全预防性维修的策略，在预防性维修间隔期内出现的故障进行最小维修，修复后故障率不变，即修复如旧，预防性维修为不完全维修，修复后产品介于修复如新与修复如旧之间，在有限期使用期（TW，UW）内确定最优的一组不完全预防性维修间隔期（T0，U0），使该批次产品的总费用最低。

1.2模型假设

1）产品是可修的，故障率随时间是递增的；

2）产品具有日历时间和使用时间两个度量指标；

3）对于给定的用户来说，其使用率r是长期恒定不变的，不同的用户使用率不同，对于批次产品而言，使用率是随机变量，用概率分布函数G（r）描述；

4）为简化模型，维修时间忽略不计；

5）产品按照时间间隔（T0，U0）进行不完全预防性维修，对于产品来说，其日历时间与使用时间二者有其一达到T0或者U0则开展相应的不完全预防性维修；

6）故障的反应时间忽略不计，即故障后立即进行维修。

1.3模型参数

1）（T0，U0）：二维预防性维修间隔期；

2）（TW，UW）：产品的使用期限；

3）Cf：故障后最小维修的费用；

4）Cp：不完全预防性维修的费用；

5）R：产品的使用率（随机变量），即每单位时间的使用情况；

6）G（r）、g（r）：产品使用率的分布函数与概率密度函数；

7）rl、ru：批次产品中最低的使用率与最高的使用率；

8）r0、rW：预防性维修间隔期 U0与 T0的比、二维使用期限UW与TW的比；

9）λ（t|r）：产品在使用率r时的故障率函数；

10）θ（m）：不完全预防性维修的改善因子，m表示维修的程度；

11）F（t|r）：产品在使用率r时的累计故障分布函数；

12）C（TW，UW）：在二维预防性维修间隔期为（T0，U0）时，产品在使用期限（TW，UW）内的期望总维修费用。

2 模型建立

为了建立二维预防性维修间隔期模型，首先需要给出二维产品的故障率函数表达式，然后进行具体的维修过程分析，根据分析的结果建立与之对应的费用函数表达式。

2.1产品二维故障率函数形式的确定

在二维产品维修领域中，共有3种不同的二维故障率表示方法，分别是双因素变量法、复合尺度法与使用率法［11］。其中使用率法的应用最为广泛，该方法中，让T（t）与U（t）分别表示产品的日历时间、使用时间与广义时间t的函数。在使用率方法中，假设U（t）=RT（t），二者为线性关系，其中R为非负的系数。由于本文假设产品的使用率为随机变量，不同的消费者对产品的使用率不同，且同一消费者的使用率保持长期恒定不变，同时R服从一定的分布，G（r）=P（R≤r），根据实际使用消费者的不同，R服从不同的分布。

产品的故障是一个点过程，通过故障率函数进行建模，根据泊松过程，产品在使用率为r时的故障率函数可以表示为

式中：φ（T（t），U（t））是关于T（t）与U（t）的增函数，这表示产品的故障率是日历时间与使用时间的增函数。Iskandar等［12］给出了如下的故障率函数公式：

Moskowitz等［13］考虑了以下形式：

Iskandar等［2］与 Yun等［14］都采用了下面的形式：

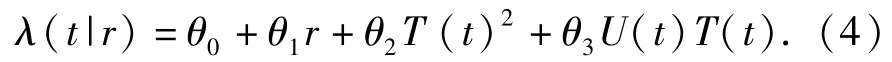
本文在第3节算例分析中也采用（4）式的形式，本文假设T（t）=t，U（t）=rt，所以最终的故障率函数表达式为

对于传统的故障率而言，故障率只是关于变量t的增函数，但是对于二维故障率来说，其是关于时间变量t与使用率变量r的增函数。通过（5）式无法直观地看到故障率与两个变量之间的最终关系，所以结合本文后续示例分析中所给出的参数，4个参数的取值为θ0=0.1，θ1=0.2，θ2=0.3，θ3=0.3时，二维故障率函数图像如图1所示。

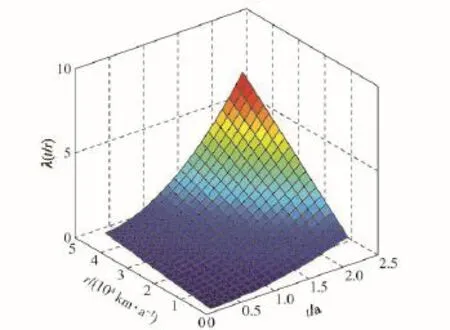
图1　二维故障率函数图像Fig.1 Two-dimensional failure rate function

由图1可以发现二维故障率函数是关于变量t 和r的增函数。这样的结果与实际中的情况也是相符的，可以证明用使用率法来表示二维故障率函数是合理的。

2.2不完全维修下故障率函数的应用

在不完全预防性维修中，产品的二维故障率会随着不完全预防性维修的实施发生改变，如图2所示。

图2　不完全维修情况下故障率变化Fig.2 Variation in failure rate under imperfect maintenance

在图2中，产品有3种不同的使用率，分别是r0、r1、r2，三者的关系为r1＞r0＞r2.传统的一维预防性维修都是在T0时刻对产品开展预防性维修，二维预防性维修对于使用率低的产品以日历时间进行预防性维修，对于使用率高的产品以使用时间提前对它进行预防性维修。如图2中r1所示，这样相对于一维预防性维修而言就可以有效地降低产品整体的维修费用。

本文考虑在产品寿命周期中的时间序列（T0，U0），2（T0，U0），…，j（T0，U0），j∈N上对产品进行二维周期不完全预防性维修，二维预防性维修间隔期为（T0，U0）。假设预防性维修工作起始时间为0，本文在Kijima［15］提出的虚拟工龄法基础上，结合Sahin等［16］对产品保修期过后维修策略的研究来处理不完全预防性维修策略建模问题。假设本阶段维修效果只与前一阶段状态相关，令vj表示第j次不完全预防性维修后产品的虚拟工龄，其中 j≥1.θ（m）表示不完全预防性维修改善因子，它是取值范围为［0，1］的关于m的减函数，因此，当维修水平m提高时，θ（m）减小，虚拟工龄减少程度就越大，即维修效果越好。令M为维修水平的最大值，此时θ（M）=0，即“修复如新”状态；当θ（0）=1时，即“修复如旧”状态。由于本文中采取的是不完全预防性维修策略，所以维修水平m的取值范围应为（0，M）。那么，对于给定的维修水平m，当产品以日历时间T0进行不完全预防性维修时，则第j次预防性维修后产品的虚拟工龄vj为

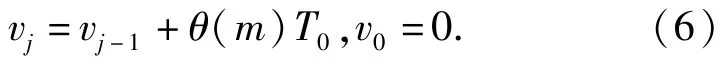
当产品以使用时间U0进行不完全预防性维修时，

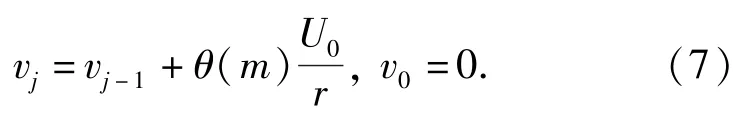
当产品以日历时间T0进行不完全预防性维修时，产品在t时刻的虚拟工龄v（t）可表示为

当产品以使用时间U0进行不完全预防性维修时，

当产品以日历时间T0进行不完全预防性维修时，产品在t时刻的故障率函数可表示为

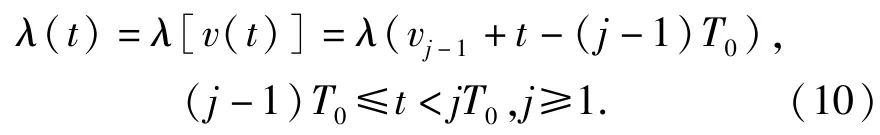
当产品以使用时间U0进行不完全预防性维修时，

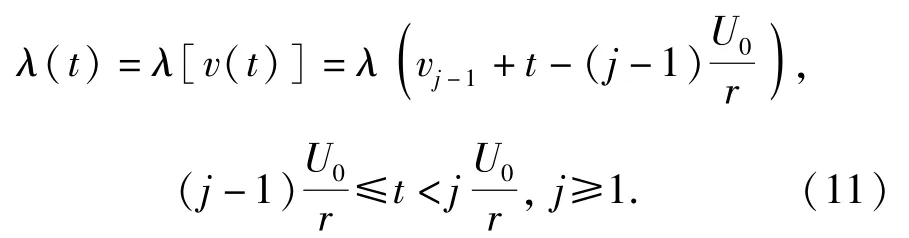
当产品以日历时间T0进行不完全预防性维修时，产品在不完全维修强度为m时的故障率函数λ（t）表达式为

式中：n表示在有限期限内完整的不完全预防性维修间隔期的个数。

当产品以使用时间U0进行不完全预防性维修时，

2.3产品的维修费用模型

对二维周期不完全预防性维修费用模型的建立分为两种情况分别进行分析讨论，分别是r0≤rW与r0＞rW.表1表示在不同的期限下开展二维不完全预防性维修的次数。

表1　不同期限下不完全预防性维修的次数Tab.1 The frequency of imperfect preventive maintenance under different periods

2.3.1r0≤rW情况时的分析

如图3所示，在这种情况下，又分为3种情况，分别是r≤r0、r0＜r≤rW和r＞rW.

图3　r0≤rW时二维预防性维修周期图Fig.3 Two-dimensional preventive maintenance cycle for r0≤rW

当r≤r0时，产品的不完全预防性维修间隔期为T0，对应的预防性维修次数为n1，即int［TW/T0］。此时产品的期望维修费用由总故障后维修费用与总预防性维修费用组成，分别用Cft与Cpt表示，此时产品的期望维修费用C 可以表示为

当r0＜r≤rW时，产品的不完全预防性维修间隔期为 U0/r，对应的预防性维修次数为 n2，即int［（TWr）/U0］，此时产品的期望费用C2为

当r＞rW时，产品的不完全预防性维修间隔期为U0/r，对应的预防性维修次数为 n3，即int［UW/U0］，此时产品的期望费用C3为

此时在有限期（TW，UW）内，r0≤rW情况下定期二维不完全预防性维修下产品的总期望费用为

2.3.2r0＞rW情况时的分析

如图4所示，情况与上文类似。当r≤rW时，产品的期望费用C4为

图4　r0＞rW时二维预防性维修周期图Fig.4 Two-dimensional maintenance preventive cycle for r0＞rW

当rW＜r≤r0时，产品的期望费用C5为

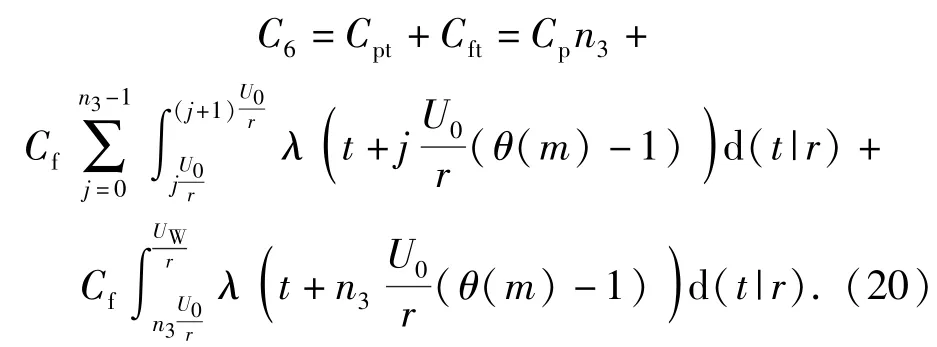
此时在有限期（TW，UW）内，r0＞rW情况下定期二维不完全预防性维修下产品的总期望费用为

综合考虑以上两种情况，即r0≤rW与r0＞rW，在有限期（TW，UW）内，定期二维不完全预防性维修下，产品的总期望费用为

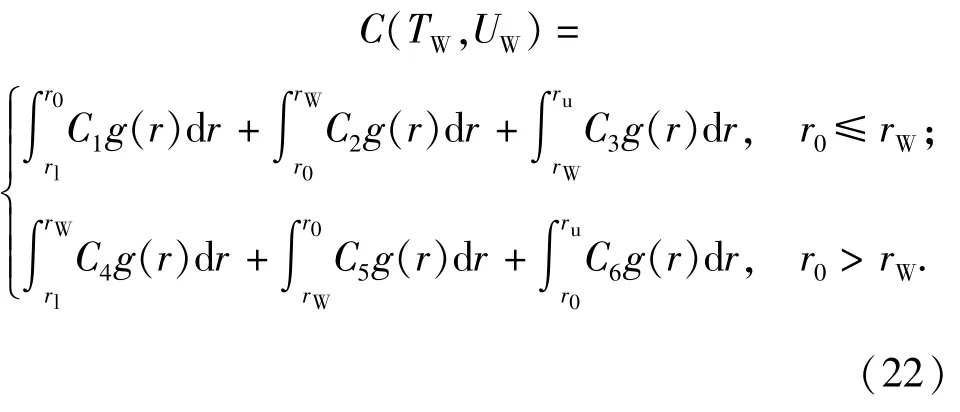
3 算例分析

3.1问题描述

在对某部队的某型按批投入使用的轮式装备调研时发现，该装备中的底盘系统只是按照传统的方式进行修复性维修，修复性维修费用很高。该装备的使用具有日历时间与使用时间（行驶里程）两个测量维度，同时发现使用率高的底盘系统出现的故障更为频繁，严重地影响到部队的正常训练。由于该装备的底盘系统是可修的产品，且维修后的效果介于修复如新与修复如旧之间。实际中的情况与上文所建模型的描述比较切合，为了降低底盘系统的维修保障费用，故对轮式装备中的底盘系统开展定期二维不完全预防性维修，在预防性维修间隔期内出现故障进行最小维修。

假设底盘系统的故障函数表达式形式为λ（t|r）=θ0+θ1r+（θ2+θ3r）t2，装备的使用期限为8 a，2×105km，根据文献［16］中所给的公式，假设不完全预防性维修程度与改善因子的关系为

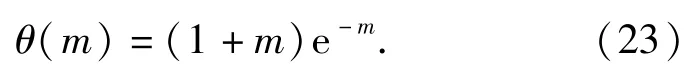
在汽车领域中，均匀分布、正态分布与威布尔分布是使用率r最为常见的分布形式［17］，为了便于比较，3种分布有相同的上下限，最高使用率 ru为5.05×104km/a，最低使用率rl为0.1×104km/a，同时假设正态分布的均值为2.5×104km/a，标准差为0.8 km/a，威布尔分布的尺度参数为2，形状参数为2.1.具体参数设置如表2所示。

表2　参数设置Tab.2 Parameter setting

将具体参数代入（22）式，可得二维不完全预防性维修费用表达式。

3.2模型优化求解

二维预防性维修是一种更先进、效果更好的预防性维修方式，本文从费用的角度对二维预防性维修间隔期进行优化决策。由于模型的表述过于复杂，无法用函数的方法对其直接求解，因此本文采用数值算法，通过Matlab仿真进行求解。根据底盘系统的故障特点选取T0与U0的适当取值范围与相应步长，生成有限组（T0，U0）；通过Matlab进行迭代计算，分别计算每组（T0，U0）所对应费用的值，绘制不同使用率分布下的二维不完全预防性维修费用模型三维图。在费用值中最小的一个所对应的（T0，U0）即为本文要求的最优二维预防性维修间隔期。

3.3结果分析

根据Matlab软件的计算结果，分别绘制出r服从均匀分布、正态分布与威布尔分布下各自的费用模型，如图5～图7所示，同时为了比较二维预防性维修与传统的一维预防性维修之间的关系，绘出图8和图9，最终根据仿真计算的结果分别如表3与

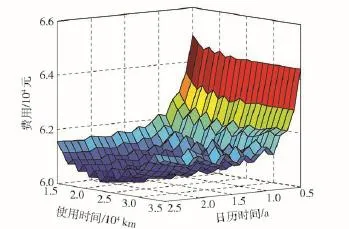
图5　均匀分布下二维费用模型Fig.5 Two-dimensional maintenance cost model under uniform distribution

图6　正态分布下二维费用模型Fig.6 Two-dimensional maintenance cost model under normal distribution

图7　威布尔分布下二维费用模型Fig.7 Two-dimensional maintenance cost model under Weibull distribution

图8　一维费用模型（按日历时间进行预防性维修）Fig.8 One-dimensional maintenance cost model with calendar time interval

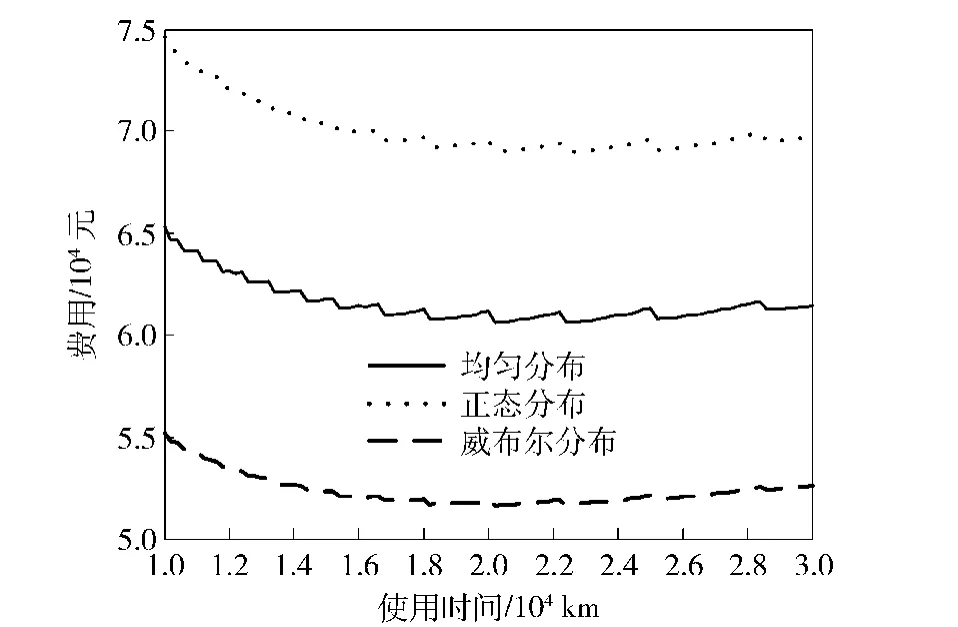
图9　一维费用模型（按使用时间进行预防性维修）Fig.9 One-dimensional maintenance cost model with service time interval

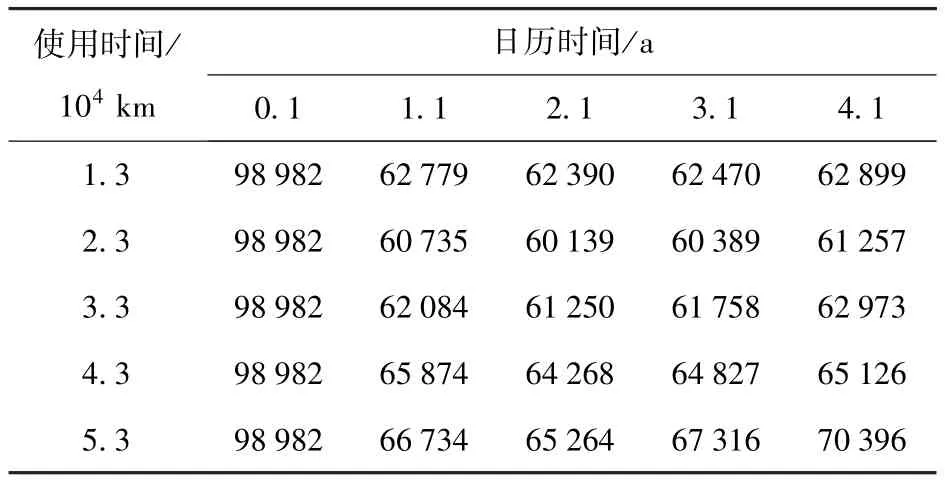
表3　均匀分布下不同间隔期费用分析表Tab.3 Cost analysis at different intervals when r subjects to uniform distribution　元

通过图5～图7可知，费用模型三维图明显是一个凹面，存在最低点，表明在以费用为约束的情况下二维周期不完全预防性维修存在最优的二维预防性维修间隔期（T0，U0）。通过计算，均匀分布最优的二维预防性维修间隔期为（2.1 a，2.3×104km），所对应的期望最低费用为60 139元；正态分布最优的二维预防性维修间隔期为（1.35 a，2.25×104km），所对应的期望最低费用为68 516元；威布尔分布最优的二维预防性维修间隔期为（1.65 a，2.25×104km），所对应的期望最低费用为50 825元。由此也可以发现使用率服从不同分布时，所优化出的最优二维不完全预防性间隔期是不同的。

通过图8与图9可知，按照传统的方法同样可以给出最优的一维不完全预防性维修间隔期。在只以日历时间进行不完全预防性维修时，均匀分布在期望费用最低时对应的最佳一维日历时间间隔期为0.9 a，正态分布与威布尔分布在期望费用最低时所对应的最佳一维日历时间间隔期分别为0.7 a与1.16 a；在只以使用时间进行不完全预防性维修时，均匀分布在期望费用最低时所对应的最佳一维使用时间间隔期为2.02×104km，正态分布与威布尔分布在期望费用最低时所对应的最佳一维使用时间间隔期分别为2.24×104km与2.02×104km.

通过表3分析可知，当使用率服从均匀分布时，不同组合下日历时间与使用时间对应的费用不尽相同。在固定日历时间T0=1.1 a时，费用随着使用时间的增加出现先降低、后升高的趋势；在固定使用时间U0=2.3×104km时，费用也随着日历时间呈现先降低、后升高的趋势。在两个变量的共同作用下，最终在（2.1 a，2.3×104km）时，取得最小值，使用率服从正态分布与威布尔分布时情况与此类似。

而在不采用任何预防性维修措施的情况下，均匀分布下装备的期望维修费用高达103 450元，正态分布与威布尔分别对应的期望费用为119 920元与85 850元，通过图5～图9以及表3、表4对比分析可知，二维预防性维修可以大大降低装备的维修保障费用，可以使装备的维修变得更为科学、合理，通过本例也进一步验证了该模型的有效性与适用性。

表4　不同分布下不同维修方式对应的费用最优值Tab.4 Optimal costs with different maintenance modes under different distributions

4 结论

本文针对故障受日历时间与使用时间双重影响的产品，提出了二维预防性维修的概念，建立了二维有限使用情况下二维周期不完全预防性维修费用模型，通过实例对比分析，验证了二维预防性维修的优越性，同时验证了模型的有效性与适用性。二维预防性维修是一个新的概念，本文只是进行了初步的探讨，研究还比较有限，下一步可以针对更为复杂的产品，采用更通用的二维故障函数表达式，选择最小维修、不完全维修以及完善维修等组合维修策略，进行二维预防性维修多目标优化的相关研究。

（References）

［1］ 陈相侄.基于不完全维修的二维产品保证成本研究［D］.杭州：杭州电子科技大学，2010. CHEN Xiang-zhi.Research on the cost of two-dimensional product warranty based on imperfect repair［D］.Hangzhou：Hangzhou Dianzi University，2010.（in Chinese）

［2］ Iskandar B P，Murthy D N P，Jack N.A new repair-replace strategy for items sold with a two-dimensional warranty［J］.Computer and Operations Research，2005，32（3）：669-682.

［3］ Chukova S，Johnston M R.Two-dimensional warranty repair strategy based on minimal and complete repairs［J］.Mathematical and Computer Modelling，2006，44（11/12）：1133-1143.

［4］ Jack N，Iskandar B P，Murthy D N P.A repair-replace strategy based on usage rate for items sold with a two-dimensional warranty ［J］.Reliability Engineering and System Safety，2009，94（2）：611-617.

［5］ Varnosafaderani S，Chukova S.A two-dimensional warranty servicing strategy based on reduction in product failure intensity［J］. Computers and Mathematics with Applications，2012，63（1）：201-213.

［6］ Chen T，Popoval E.Maintenance policies with two-dimensional warranty［J］.Reliability Engineering and System Safety，2002，77（1）：61-69.

［7］ 甘茂治，康建设，高崎，等.军用装备维修工程学［M］.北京：国防工业出版社，2005：210-211. GAN Mao-zhi，KANG Jian-she，GAO Qi，et al.Military equipment maintenance engineering［M］.Beijing：National Defense Industry Press，2005：210-211.（in Chinese）

［8］ Yeh R H，Chen M Y，Lin C Y.Optimal periodic replacement policy for repairable products under free-repair warranty［J］.European Journal of Operational Research，2007，176（3）：1678-1686.

［9］ Shahanaghi K，Noorossana R.Failure modeling and optimizing preventive maintenance strategy during two-dimensional extended warranty contracts［J］.Engineering Failure Analysis，2013，28：90-102.

［10］ Hu Q W，Bai Y S，Zhao J M，et al.Modeling spare parts demands forecast under two-dimensional preventive maintenance policy［J］.Mathematical Problems in Engineering，2015，2015：1-9.

［11］ Shafiee M，Chukova S.Two-dimensional warranty cost analysis for second-hand products［J］.Communications in Statistics— Theory and Method，2011，40（4）：684-701.

［12］ Iskandar B P，Murthy D N P.Repair-replace strategies for twodimensional warranty policies［J］.Mathematical and Computer Modelling，2003，38（11/13）：1233-1241.

［13］ Moskowitz H，Chun Y H.A poisson regression model for two-attribute warranty policies［J］.Naval Research Logistics，1994，41（3）：355-376.

［14］ Yun W Y，Kang K M.Imperfect repair policies under two-dimensional warranty［J］.Journal of Risk and Reliability，2007，221（4）：239-247.

［15］ Kijima M.Some results for repairable systems with general repair ［J］.Journal of Applied Probability，1989，26（1）：89-102.

［16］ Sahin I，Polatoglu H.Maintenance strategies following the expiration of warranty［J］.IEEE Transactions on Reliability，1996，45（2）：220-228.

［17］ Huang Y S，Chen E，Ho J W.Two-dimensional warranty with reliability-based preventive maintenance［J］.IEEE Transactions on Reliability，2013，62（4）：898-907.

Research on Optimization of Two-dimensional Imperfect Preventive Maintenance Intervals of Products

HAN Yu-cheng，JIA Xi-sheng，BAI Yong-sheng，LI Xin-yue
（Department of Equipment Command and Management，Ordnance Engineering College，Shijiazhuang 050003，Hebei，China）

For the products of which the failures are affected by the calendar time and service time，the traditional one-dimensional preventive maintenance can’t meet the actual demand.A concept of two-dimensional preventive maintenance is proposed.The two-dimensional preventive maintenance decision is made according to calendar time and service time.A failure rate function expression of two-dimensional maintenance is established，and the process of two-dimensional imperfect preventive maintenance is analyzed in detail.A cost model of two-dimensional imperfect preventive maintenance is proposed to minimize the consumer’s total expected cost in finite life span.An optimal two-dimensional imperfect preventive maintenance interval is derived through examples，and the the applicability and validity of the proposed model are verified through comparison and analysis.A brief discussion about future research area of two-dimensional maintenance is presented.

ordnance science and technology；two-dimensional imperfect preventive maintenance；math model；virtual age

TJ07

A

1000-1093（2016）03-0496-09

10.3969/j.issn.1000-1093.2016.03.015

2015-07-29

国家自然科学基金青年科学基金项目（71401173）

韩玉成（1990—），男，硕士研究生。E-mail：hanyucheng805@163.com；贾希胜（1964—），男，教授，博士生导师。E-mail：xsh_jia@hotmail.com