双循环圆液力缓速器叶片顶弧优化设计
穆洪斌,魏巍,2,闫清东,2,刘城
(1.北京理工大学机械与车辆学院,北京100081;2.北京理工大学车辆传动国家重点实验室,北京100081)
双循环圆液力缓速器叶片顶弧优化设计
穆洪斌1,魏巍1,2,闫清东1,2,刘城1
(1.北京理工大学机械与车辆学院,北京100081;2.北京理工大学车辆传动国家重点实验室,北京100081)
为提高双循环圆液力缓速器制动效能,对其弯叶片顶弧参数进行优化设计。基于叶片顶弧参数化设计方法,建立缓速器内流道计算模型。以顶弧半径与顶弧间距为设计变量,利用三维流场仿真技术进行试验设计研究,并开展制动力矩影响参数的敏感性分析。通过构建制动力矩近似模型,采用梯度优化算法进行寻优以得到优化结果。就设计参数对液力缓速器内流场流动状态与制动外特性影响开展分析,并与样机仿真以及试验数据进行对比。结果表明,优化后缓速器制动性能得到明显提高,制动力矩平均增幅可达70.8%,且叶片结构满足强度要求。
动力机械工程;双循环圆;液力缓速器;顶弧;优化设计
0 引言
为提高液力缓速器的制动效能,现有的缓速器内腔多采用无内环的结构形式,即油液进出动、定轮通过同一平面完成,两叶轮间没有明确的进出油口。当油液流经叶片顶廓进行循环流动时,受其结构形式影响会在叶轮进出油口附近形成不稳定流动,产生一定的扩散与收缩损失,抑制了油液在循环圆中的流动速度。而在其他几何参数不变的情况下,油液的循环流速决定了其循环流量大小。由束流理论可知,循环流量又决定了缓速器的制动力矩,且呈现正相关性。综上所述,由于没有内环结构,叶片顶廓的结构形式直接影响了油液在缓速器动、定轮进出油口处的流动状态与循环流速,因此其应成为提高缓速器制动性能的研究重点之一。
双循环圆液力缓速器具有制动功率大,径向尺寸小,动轮轴向载荷小等优点[1-2],其叶片多采用弯叶片结构,叶片整体呈弯曲状,其工作面与叶轮入出口平面夹角约为90°,即叶片径向顶廓与整体叶形保持一致,图1为某双循环圆液力缓速器结构图。文献[3-4]针对弯叶片结构形式,提出参数化设计方法,对其径向叶形开展了优化设计研究,并揭示了各叶形参数对制动力矩的影响。
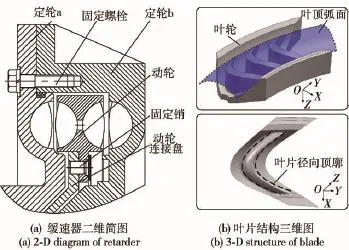
图1 双循环圆液力缓速器结构图Fig.1 Structure of dual torus hydrodynamic retarder
弯叶片顶廓为圆弧绕缓速器轴线回转生成,这里将此叶顶弧面简称为“顶弧”,如图1(b)所示。本文在前期研究基础上[3-4],针对双循环圆液力缓速器弯叶片顶弧,基于参数化设计方法,搭建优化设计仿真平台。结合试验设计、近似模型及梯度优化算法[5],对叶片顶弧开展优化设计研究。
1 几何模型

图2 叶片顶廓结构简图Fig.2 Schematic diagram of blade top profile
基于径向叶形参数建模方法[3],针对叶片顶廓结构,建立相应的参数化设计模型。图2为双循环圆液力缓速器弯叶片顶廓结构简图。
对于叶片顶弧,定义其与动、定轮交互面最小间距即顶弧间距为zt;轴面轮廓呈圆弧状,定义其顶弧半径为rt,如图2(b)所示。其中,动、定交互面是为数值计算方便而假想规定的平面。定义交互面与叶轮入出口面间距为zi,工作腔循环圆半径为R.其中,zi与R均为常值。由此可提出叶片顶弧设计参数,记为


式中:{Cxy}为径向叶形轮廓点集;点P、Q、S分别为叶片径向顶廓边界点。为避免动、定轮叶片相互干涉,并满足几何结构与实际加工要求,令边界点P、Q位于上,点S处于交互面A'B'左侧,且圆心角小于180°.
根据上述限定条件,在参数设计区间内,将设计参数zt与rt离散化,用以绘制有效设计点分布范围,如图3所示。其中,zt与rt预先取定的范围为

由图3可见,有效设计点分布在一个连续空间里,而无效计算点则分布在a、b两个无效区中。因此,在进一步的数值计算与优化设计中,应将设计点更多地取定在图中蓝点分布范围内,以提高优化设计效率。
图4为只改变参数rt而zt保持不变的定轮周期流道设计模型,由此可看出rt的不同取值对叶片顶廓(蓝线所示)设计结果的影响。
2 优化设计
将弯叶片顶弧参数rt与zt作为设计变量,以提高制动力矩为优化目标,开展优化设计研究。由图3可知,当无效区 a出现时,rt取值需大于120 mm,而工作腔循环圆半径R仅为19 mm,因此为减小计算量,暂且忽略无效区a,取顶弧参数设计空间如下:

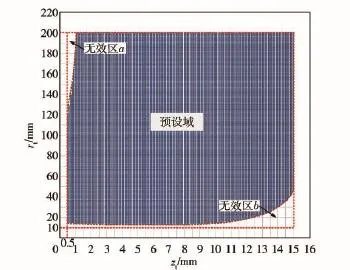
图3 有效设计点分布图Fig.3 Distribution of effective design points

图4 定轮流道设计结果(黑线为流道轮郭,蓝线为叶片顶廓)Fig.4 Design results of stator flow passage(black line:flow passage profile;blue line:blade top profile)
在设计计算前,须对模型可信度进行分析,并在保证计算精度的前提下尽量降低计算时间[6]。文献[3]对模型计算方法与网格独立性进行了研究,证明了数值计算方法具有良好的计算精度,且计算用时较少。
为了缩短寻优过程,采用优化拉丁方设计方法进行试验设计(DOE),基于径向基函数(RBF)神经网络方法构建制动特性近似模型,利用梯度优化算法在近似曲面上寻取优化解[7],并对优化结果进行三维流场数值验算,设计流程如图5所示。
在参数区间内开展DOE,生成400组均布的设计点[8-9],通过计算流体力学(CFD)求解计算,获得各参数对应下的计算结果,其中可行解数目为327个。基于DOE试验样本计算结果,就设计参数rt与zt对制动力矩的影响进行分析。图6为取动轮转速1 000 r/min时,两参数对制动力矩T的敏感性分析图。
图6(a)和图6(b)为参数rt与zt对制动力矩T的主效应图,表征了因变量随单自变量的变化规律。由图6(a)和图6(b)可见,制动力矩随zt的增加呈递减的趋势,而随着rt增大,制动力矩先增大,后减小,当rt取在17 mm附近,制动力矩出现极大值。对比图6(a)和图6(b)可见,在取定的设计区间中,zt对制动力矩影响范围更大。图6(c)为rt与zt两参数对制动力矩的交互效应图,反映了自变量共同对因变量影响的关系与程度。由图6(c)可见,随着zt的增加,rt分别处于“高”,“低”水平下对应的制动力矩曲线存在相交,说明参数rt与zt存在一定的交互性。另外,图6(d)为表征各参数对制动力矩影响程度的Pareto图,主要有线性相关程度、平方相关程度、自变量交互影响程度。由图6(d)可见,zt与制动力矩具有明显的线性相关性,贡献率Rp占总体的58%,而zt与rt的交互效应对制动力矩亦有明显影响,贡献率Rp占总体的21%.
采用RBF模型进行近似模型的构造,其对制动数据的拟合度达到了99.8%,拟合效果良好,保证了寻优精度。基于近似模型,建立制动力矩关于rt与zt的二维等值线图,如图7所示。由图7可见,在位于设计区间边缘处,优化目标存在一个明显的峰值,即当zt处于15 mm附近,rt处于1 mm附近出现制动力矩的极大值点,但此处亦存在无效设计区b,因此为了得到优化的设计结果,需要使用合适的优化算法进一步寻优。
在弯叶片顶弧优化设计中,其设计空间具有单峰性与连续性,因而采用梯度优化算法,通过设置初始点,即可获得良好的优化结果。经过195次循环迭代,得到优化解为

将优化解Xz代回原模型,进行CFD验算后的制动力矩Ty=6 122 N·m.由此可见,基于RBF与梯度优化方法获得的优化制动力矩较为精确,相对误差仅为0.87%.
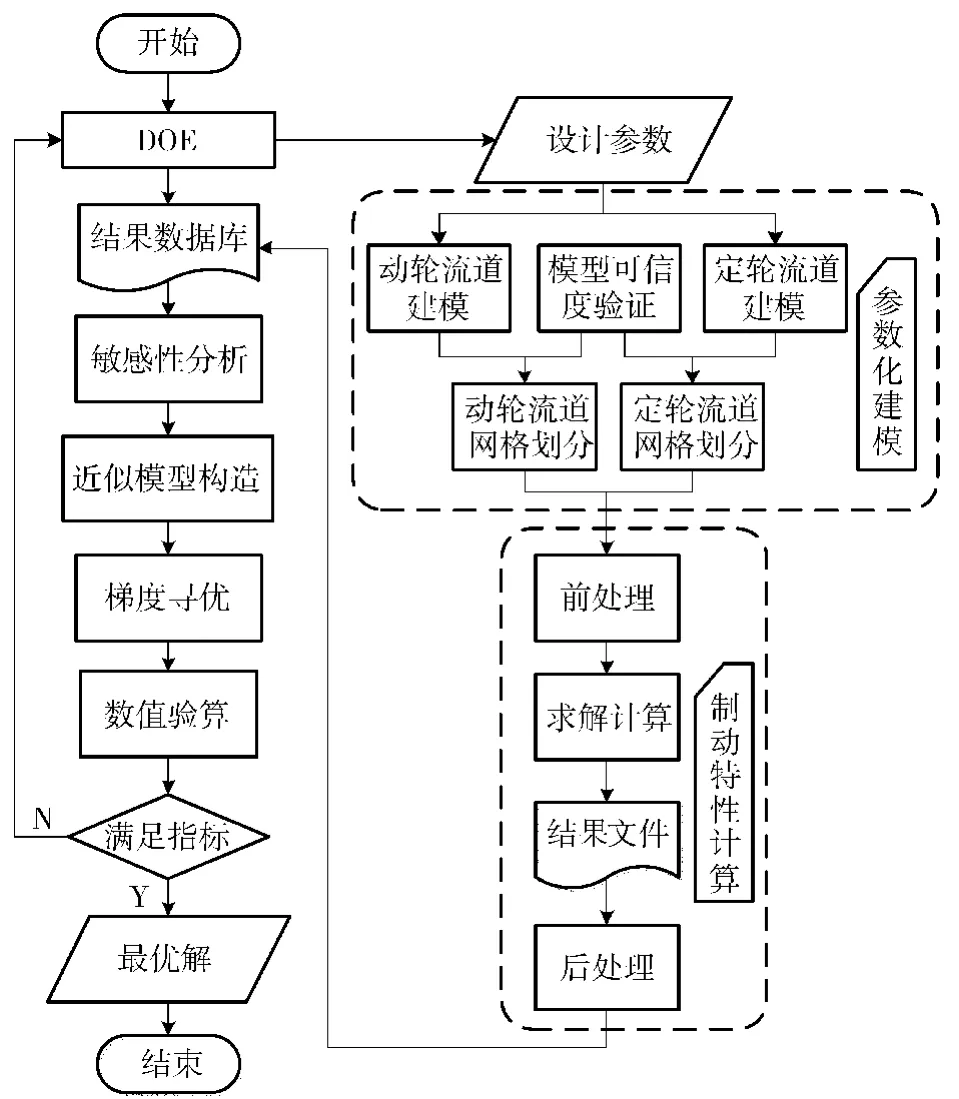
图5 优化设计流程图Fig.5 Flow chart of optimization design
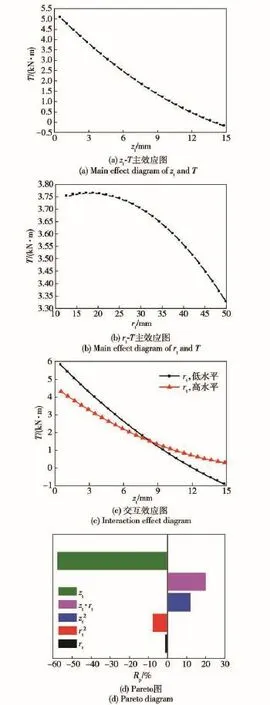
图6 参数敏感性分析图Fig.6 Analysis graphics of parameter sensitivity
3 制动特性对比分析
基于叶片顶弧优化设计结果,分别对两参数数值进行修改,获得两个对比方案,以分析顶弧参数对制动性能的影响。同时,对相同工况下样机叶片进行数值模拟,进行对比研究。其中,优化方案与对比方案的径向叶形参数与样机叶片一致。优化方案、样机方案、对比方案顶弧参数如表1所示。
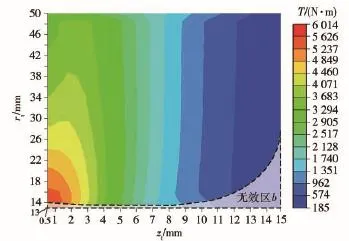
图7 等值线图Fig.7 Contour map

表1 各方案参数表Tab.1 Parameters of each scheme

图8 定轮周期面与交互面速度矢量分布图Fig.8 Velocity vector distribution of stator periodic and interactive surfaces
图8为定轮流道周期面与交互面速度矢量分布情况。整体可见,4个方案油液均呈明显的循环流动,低速区出现在循环圆中部,定轮入口处流速最高,随着油液高速冲击定轮叶片,导致其流速不断降低,而后油液脱离叶片,其流动阻力减小,因此在定轮出口处油液速度略有增加。
从优化方案到对比方案,优化方案中油液整体流速更高,循环流道从外到内的油液流速变化梯度亦更大,因此所形成的涡旋区(A、B、C处)更为明显,其单流道循环流量Qo高达404 L/min.对于对比方案1,与优化叶片相比,其顶弧曲率更小,导致油液经过叶片流入与流出轮腔的空间狭小(D、E处),收缩与扩散阻力增加,油液循环流速受到抑制,其循环流量Q1仅为313 L/min.对于对比方案2,其顶弧半径与优化方案一致,但其顶弧间距zt较大,导致叶片有效冲击面积减小,叶片对油液流动的导向性减弱,因此对比方案2中油液整体流速较低,涡旋区亦不明显,其循环流量Q2也仅为301 L/min.至于样机方案,其整体流速与循环流量Qp介于优化方案与对比方案之间。
在定轮入口处,绕缓速器旋转轴(z向)做入口截面,如图9所示,图10即为定轮入口截面速度矢量分布图。整体可见,高速油液流入叶片吸力面入口处,在图中A处形成加速区,而后在叶片导向作用下,沿着叶片弯曲方向流动。对比4个方案可以明显看出,优化方案油液流速最高,与图8描述一致。
图11展示了定轮入口截面x与z方向上的速度梯度分布情况,速度梯度值可以表征流体与流体,以及流体与壁面接触处的黏性力大小,即能量损失大小。由图11可见,无论是优化方案还是对比方案,速度梯度极大值均出现在叶片顶部靠近吸力面位置(A、B处),亦如图10中A处所示。对比图11中各方案可以看出,对比方案1中叶片对入口油液流动的阻碍作用显著,因而其速度梯度变化最为剧烈,产生的能量损失也更高,抑制了整体的循环流量大小,对比方案2中油液的速度梯度最小,但由于其整体流速较低,因此循环流量亦较小,而对于样机方案,其高梯度区域也较明显,分布范围略小于对比方案1,表明样机顶廓也会对油液流动造成较强的阻碍。

图9 定轮入口截面图Fig.9 Sectional view of stator inlet

图10 定轮入口截面速度矢量分布图Fig.10 Velocity vector distribution of stator inlet section

图11 定轮入口截面速度梯度分布图Fig.11 Velocity gradient distribution of stator inlet section
由前文分析可知,优化方案油液整体流速较样机方案有了显著提升,即油液对叶轮叶片冲击作用增强,叶片所受应力亦增加。因此,有必要对优化结果的叶轮强度进行校核,以保证缓速器在极限工况下的安全使用。液力缓速器样机在动轮转速1 000 r/min时,工作腔近似达到全充液状态,此时缓速器产生最大制动效能。因此,在此制动工况下,对优化方案叶轮进行单向流体-固体耦合分析,得到优化后缓速器叶轮等效应力分布,如图12所示。
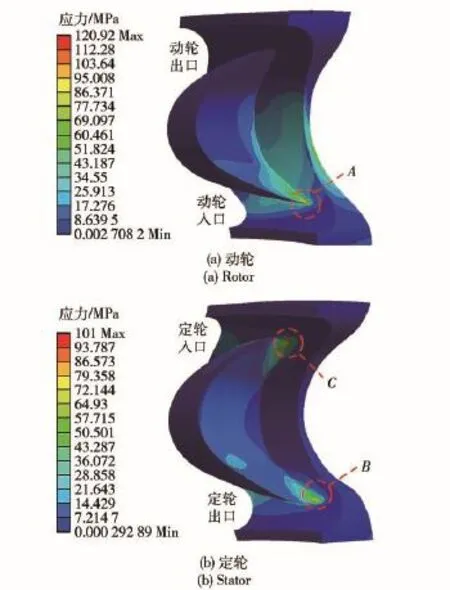
图12 优化方案叶轮等效应力分布Fig.12 Equivalent stress distribution of optimized impeller
由图12可见,动、定轮叶片所受的等效应力极大值均出现在叶片下部与流道内壁交界处(A、B处);另外,在定轮叶片上部与流道内壁交界处(C处)亦出现应力极大区域。定轮叶片最大等效应力值为101 MPa,动轮由于同时受到离心力作用,其最大等效应力值较高,达到了120.92 MPa.优化方案中叶轮材料拟采用合金钢,其抗拉强度高于840 MPa.显然,在此工况下,动、定轮叶片所受的应力值均明显小于材料强度极限,即优化方案满足强度要求。
图13为优化方案、对比方案、样机方案制动力矩计算结果以及样机台架试验数据对比图。在分析转速区间内,样机仿真结果与试验数据吻合较好,平均相对误差仅为4.8%.由于仿真过程未考虑缓速器工作腔进出口以及叶片铸造圆角对流场产生的影响,因此计算误差在可接受范围,证明了此数值计算方法具有良好的可靠性,应用相同计算方法的优化与对比方案数值结果亦应具有一定可信度。
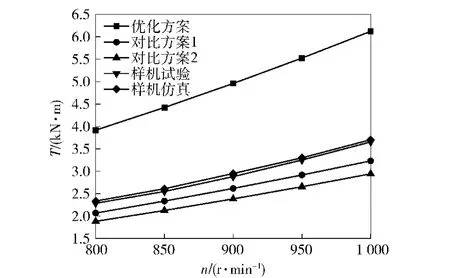
图13 制动特性对比图Fig.13 Comparison of brake performances
两对比方案制动力矩远低于优化方案计算值,结合上文流场分析结果可知,任一设计参数取值较大时,均会对缓速器制动性能产生不利影响,因此忽略rt>50 mm的情况,并不会影响优化解的获取。另外,优化方案制动力矩整体高于样机计算结果,其力矩增幅可达70.8%.由此可见,在缓速器循环圆尺寸与径向叶形参数不变的情况下,通过改变叶片顶弧参数rt与zt可以有效提高缓速器的制动效能。
4 结论
1)提出了双循环圆液力缓速器叶片顶弧参数化设计方法,明确了有效设计点分布范围,实现了缓速器内流道模型的快速生成。
2)结合优化拉丁方设计方法、神经网络模型及梯度优化算法,对双循环圆液力缓速器叶片顶弧参数进行了优化设计。结果表明,本文采用的优化方法适用于弯叶片顶弧参数优化,具有较高精度。
3)制动特性对比分析结果表明,叶片顶弧参数rt与zt均会对缓速器制动性能产生较大影响。优化方案流场速度分布值与循环流量均最大,且较样机计算结果,其制动力矩平均可提高70.8%,且叶轮叶片结构满足强度要求。
(References)
[1] Allison Transmission Inc.MD/HD/B series on-highway transmissions operator’s manual[M].Indiana:Allison Transmission Inc,2005.
[2] Allison Transmission Inc.3000/4000 operator’s manual[M].Indiana:Allison Transmission Inc,2010.
[3] 闫清东,穆洪斌,魏巍,等.双循环圆液力缓速器叶形参数优化设计[J].兵工学报,2015,36(3):385-390. YAN Qing-dong,MU Hong-bin,WEI Wei,et al.Design optimization of blade parameters of dual torus hydraulic retarder[J].Acta Armamentarii,2015,36(3):385-390.(in Chinese)
[4] 穆洪斌,闫清东,魏巍,等.不同叶型双循环圆液力缓速器制动性能与流动特性对比分析[J].液压与气动,2015(4):18-23. MU Hong-bin,YAN Qing-dong,WEI Wei,et al.Comparative analysis of braking performance and flow characteristics for dual torus hydraulic retarder with different blades[J].Chinese Hydraulics&Pneumatics,2015(4):18-23.(in Chinese)
[5] 王健,葛安林,雷雨龙,等.基于三维流动理论的液力变矩器设计流程[J].吉林大学学报:工学版,2006,36(3):315-320. WANG Jian,GE An-lin,LEI Yu-long,et al.Design flow of torque converter based on three dimensional flow theory[J].Journal of Jilin University:Engineering and Technology Edition,2006,36(3):315-320.(in Chinese)
[6] Habashi W G,Fortin M,Vallet M G,et al.Anisotropic mesh adaptation:towards user-independent,mesh-independent and solver-independent CFD solutions.PartⅠ:theory[J].International Journal for Numerical Methods in Fluids,2000,32(6):725-744.
[7] 罗虹,李英强,李兴泉,等.液力变矩器叶片参数的正交试验优化设计[J].兵工学报,2012,33(7):782-787. LUO Hong,LI Ying-qiang,LI Xing-quan,et al.Optimal design of vanes in hydrodynamic torque converter based on orthogonal DOE[J].Acta Armamentarii,2012,33(7):782-787.(in Chinese)
[8] Jin R C,Chen W,Sudjlanto A.An efficient algorithm for constructing optimal design of computer experiments[J].Journal of Statistical Planning and Inference,2005,134(1):268-287.
[9] Alejandro S H.Breaking barriers to design dimensions in nearly orthogonal Latin hypercubes[D].Monterey,California:Naval Postgraduate School,2008.
Optimization Design of Blade Top Arcs of Dual Torus Hydrodynamic Retarder
MU Hong-bin1,WEI Wei1,2,YAN Qing-dong1,2,LIU Cheng1
(1.School of Mechanical Engineering,Beijing Institute of Technology,Beijing 100081,China 2.National Key Lab of Vehicle Transmission,Beijing Institute of Technology,Beijing 100081,China)
In order to improve the braking efficiency of dual torus hydrodynamic retarder,the parameter optimization design of blade top arcs is studied.A numerical model of internal flow passage is established based on the parametric modeling method of blade top arcs.The computational fluid dynamics method is used for design of experiments with the radius and distance of blade top arcs as design variables,and the sensitivity analysis of two parameters having the effect on brake performance is made.A gradient optimization algorithm is used to get the optimum result by building an approximate model of braking torque. The influence of design parameters on internal flow field and external brake performance is analyzed,and the simulated results are compared with the experimental data.The results show that the brake performance of hydrodynamic retarder after optimization is significantly improved,the braking torque is increased by 70.8%,and the blade structure meets the strength requirement.
power machinery engineering;dual torus;hydrodynamic retarder;top arcs;optimization design
TP137.332
A
1000-1093(2016)03-0400-08
10.3969/j.issn.1000-1093.2016.03.003
2015-07-07
国家自然科学基金项目(51475041);车辆传动国家重点实验室基金项目(9140C35020905)
穆洪斌(1989—),男,博士研究生。E-mail:muhongbin_bit@126.com;闫清东(1964—),男,教授,博士生导师。E-mail:yanqd@bit.edu.cn;魏巍(1978—),男,副教授,博士。E-mail:weiweibit@bit.edu.cn

