基于非对称模型的欠驱动无人海洋运载器轨迹跟踪控制

董早鹏，万磊，孙玉山，刘涛，李岳明，张国成

（1.哈尔滨工程大学水下机器人技术重点实验室，黑龙江哈尔滨150001；2.哈尔滨工程大学船舶工程学院，黑龙江哈尔滨150001）

基于非对称模型的欠驱动无人海洋运载器轨迹跟踪控制

董早鹏1，2，万磊1，2，孙玉山1，2，刘涛1，李岳明1，2，张国成1，2

（1.哈尔滨工程大学水下机器人技术重点实验室，黑龙江哈尔滨150001；2.哈尔滨工程大学船舶工程学院，黑龙江哈尔滨150001）

研究一类欠驱动无人海洋运载器（UMV）的轨迹跟踪控制问题，提出了一种基于非对称模型的积分反步控制方法。建立了非完全对称（左右对称、前后不对称）的欠驱动UMV水平面运动模型，考虑了系统阻尼系数矩阵和惯性系数矩阵非对角线元素存在非零项的问题；通过设计虚拟状态和控制输入反馈变换，解决了UMV轨迹跟踪控制过程中存在的角速度持续激励问题，得到了直线轨迹和曲线轨迹通用的跟踪控制器；在轨迹跟踪控制器当中引入跟踪误差的积分项，提高了UMV系统的全局稳定收敛速度，基于Barbalat引理和Lyapunov稳定性理论分析了系统的稳定性。借助实验室半物理仿真平台进行仿真实验，与传统基于对称模型的控制算法对比，体现出了基于非对称模型的欠驱动UMV轨迹跟踪控制方法的优越性。

控制科学与技术；无人海洋运载器；非对称模型；欠驱动控制；轨迹跟踪；积分反步法

0 引言

伴随着全球海洋开发和海军装备竞争热潮的涌起，无人海洋运载器（UMV）的研制越来越受到世界各国科研人员的关注与重视［1-3］；UMV通常包括无人水下机器人（UUV）和水面无人艇（USV）两大类［4-5］，由于它们具有无人化、智能化等特点且通常具备搜索、测量、数据与信息搜集、辅助通信和导航、跟踪定位与循迹等功能，因而备受各国海军和海洋开发机构的关注和重视［6-7］。UMV的轨迹跟踪控制技术是它完成各项使命的关键技术之一，近年来已有部分学者对其进行了研究，取得了一定的成果。UMV的运动通常可分解为水平面运动和垂直面运动，由于它们具有一定的相似性，因而目前大多数UMV的运动控制技术研究主要集中在其水平面运动控制问题方面［8-9］。

Xia等［10］、Chen等［11］、Yang等［12］研究了一类全驱动UMV的轨迹跟踪问题，而出于成本与实际使用性能等方面的考虑，目前大多数UMV均设计为欠驱动形式［13-14］，因此文献［10-12］中控制方法的推广使用存在一定的局限性。Harmouche等［15］、Liao等［16］讨论了 UMV的曲线轨迹跟踪问题，由于均存在角速度持续激励的假设条件，因而所设计控制器无法进行直线轨迹的跟踪控制。董早鹏等［17］、Katayama等［18］研究了UMV的直线轨迹跟踪控制问题，同样他们所提出的直线跟踪控制方法对曲线轨迹的跟踪又存在一定的使用限制。文献［19-23］基于自抗扰控制技术、非线性反步法、滑模法等现代非线性控制方法，文献［24-26］基于模糊滑模反步法、自适应神经网络反步法等混合智能控制技术，研究了UMV的轨迹跟踪控制问题，其中对于UMV的模型均考虑为完全对称（前后、左右均对称），忽略了前后不对称性的影响。对于模型非对称性在UMV运动控制方面的研究，万磊等［27-28］基于复杂的多次微分同胚变换和级联系统理论进行了讨论，仅是采用了非对称模型对运动控制问题进行分析，而并没有深入的研究非对称模型对控制系统性能的影响。

虽然针对UMV轨迹跟踪问题的研究目前已经取得了不少的成果，但通过上述分析可知，对于其中的欠驱动控制、角速度持续激励、控制器的直线和曲线轨迹跟踪通用性、模型非对称性影响分析等问题，目前还没有相关文献进行综合统一的详细论述。本文在上述已有研究成果的基础上，基于积分反步法设计了一种能够同时解决上述问题的UMV轨迹跟踪控制器，并对模型非对称性对控制性能的影响进行了详细的分析和讨论。

1 UMV轨迹跟踪问题描述

1.1UMV运动建模

欠驱动UMV的水平面三自由度运动学和动力学模型［9］如下：

式中：η=［x，y，φ］T，x、y、φ分别为UMV在大地坐标系下的纵向位置、横向位置、艏摇角度；ν= ［u，v，r］T，u、v、r分别为UMV的纵荡速度、横荡速度、艏摇角速度；τ=［τu，0，τr］T，τu、τr分别为推进器和舵给UMV的纵向力和转艏力矩，由于欠驱动UMV不含侧推，因而横向控制力为0；R（φ）、M、C（ν）、D分别为UMV系统的艏摇旋转矩阵、惯性系数矩阵、科氏力和向心力矩阵、阻尼系数矩阵，它们定义如下：

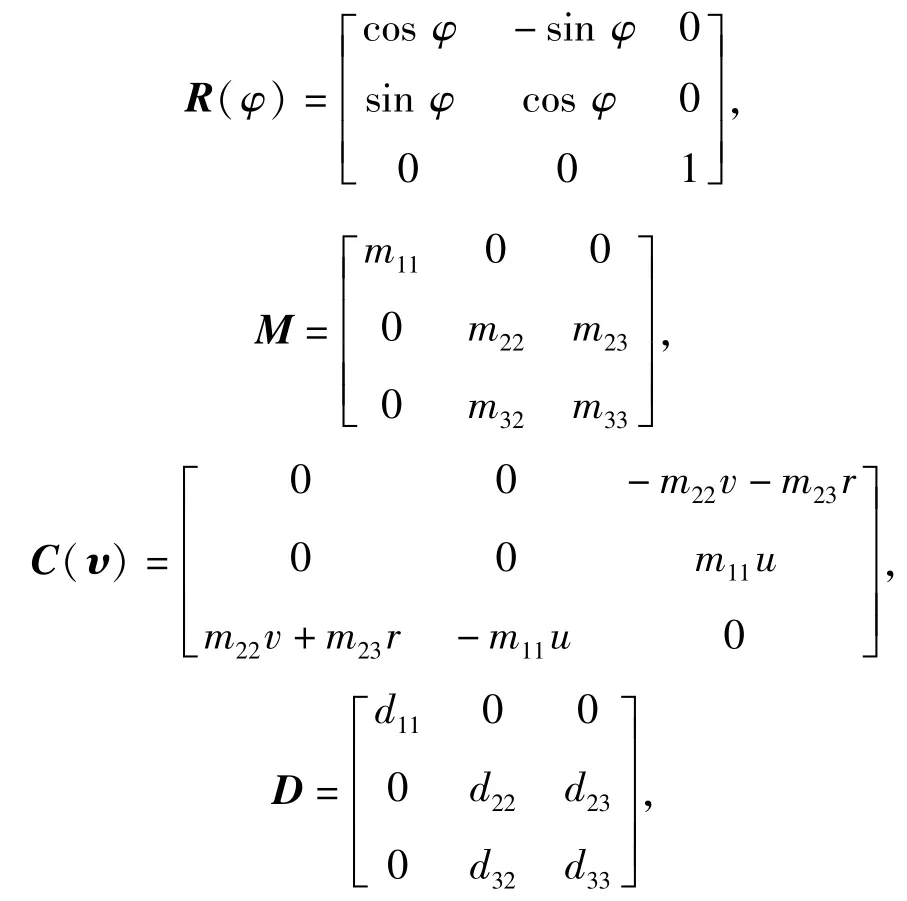
1.2轨迹跟踪模型设计

对（1）式中第一个表达式两边求导可得

（1）式第2个表达式可变换为

将（3）式带入（2）式可得

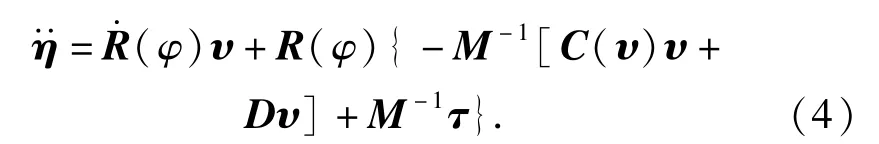
对（4）式移项化简可得

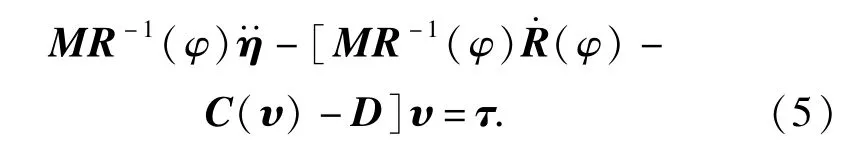
展开（5）式可得

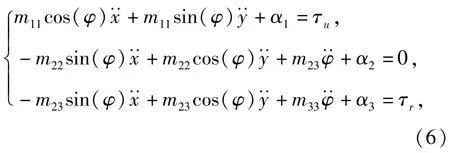
定义如下变量：

设计输入反馈变换：

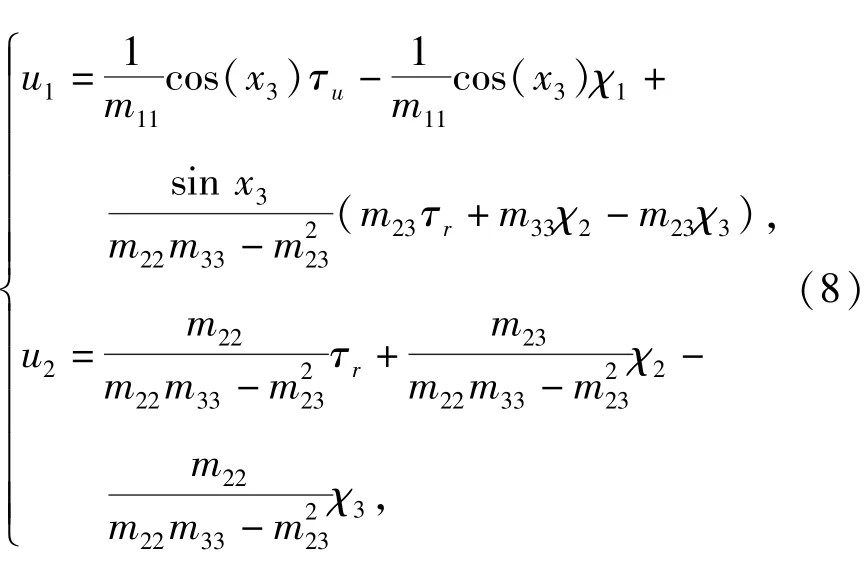
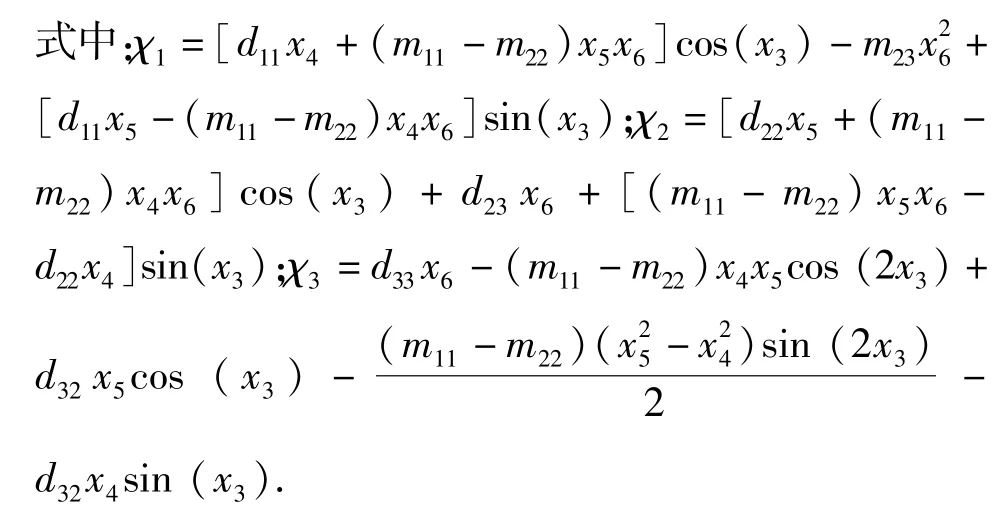
则系统（6）式可以转换为

同理，对参考目标轨迹进行类似变换可得

定义如下轨迹跟踪误差变量

对（11）式两边求导可得

至此，UMV轨迹跟踪控制问题转换为了跟踪误差系统（12）式的镇定控制问题。

2 控制器设计

UMV轨迹跟踪控制系统设计主要包括3大部分：系统模型变换、控制输入设计、控制执行与反馈，如图1所示。

本节主要研究由跟踪误差变量设计执行器所需要的最终控制输入，同时使得整个轨迹跟踪控制系统全局稳定。首先设计变量

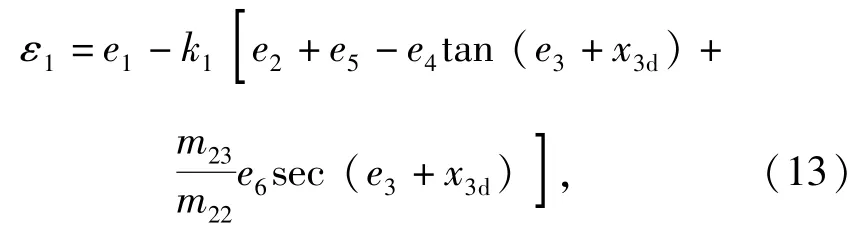
对（13）式求导可得

图1　轨迹跟踪控制系统设计流程图Fig.1 Flow chart of trajectory tracking control system design

式中：

设计变量：

则

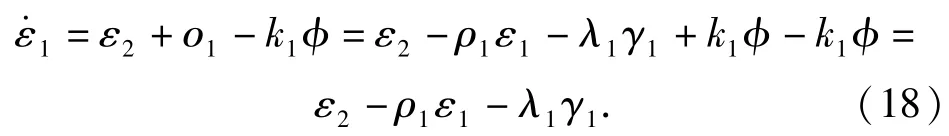
对（17）式求导可得

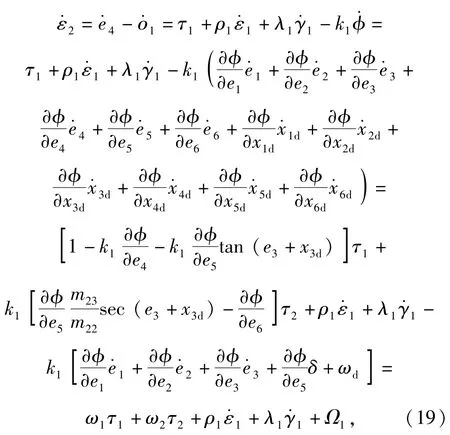
设计变量：

对（20）式求导可得

定义变量：

则有

对（24）式求导可得

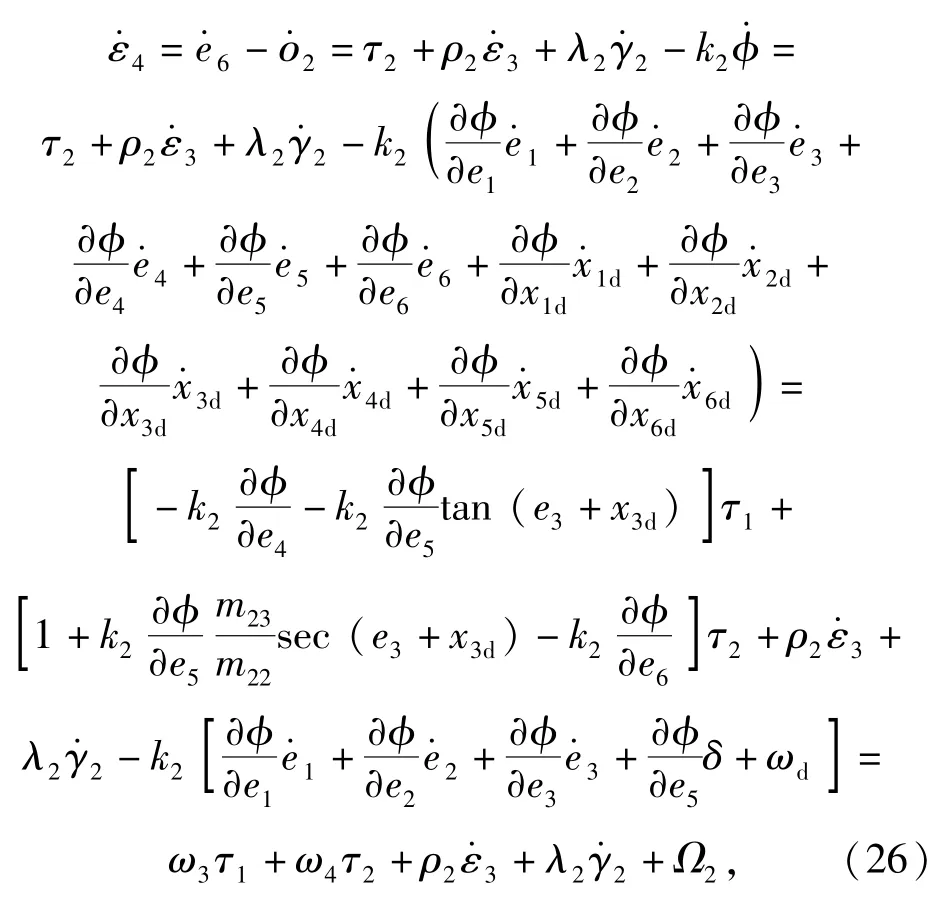
根据（19）式、（26）式，可设计控制律：

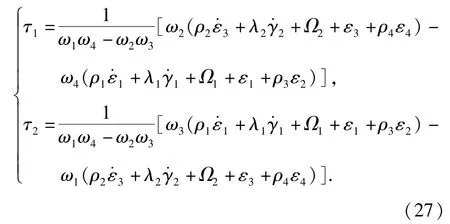
根据（8）式、（12）式、（27）式，可得UMV轨迹跟踪控制律：

3 稳定性分析

定理 对于由（29）式生成的参考轨迹：

式中：ud（t）和rd（t）分别为任意给定的UMV参考速度和角速度，它们决定了参考轨迹的形式。对于任意初始状态的UMV和任意给定的参考速度和角速度，轨迹跟踪控制律（28）式可使跟踪误差（30）式全局成立：

即证明所设计控制律能够实现任意参考轨迹的跟踪控制。

证明 分3步证明定理：

1）将（27）式代入（19）式、（26）式，联合（15）式、（18）式、（22）式和（25）式可得

考虑如下Lyapunov函数：

对（32）式求导可得

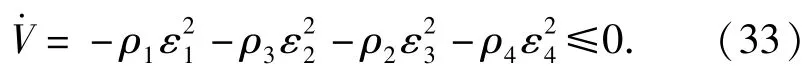
（33）式表明Lyapunov函数递减，从而V（t）＜V（0），因此均有界，同时由（31）式可知均有界。对求导可得

2）由于k1、k2为选择参数，根据（13）式、（20）式和（35）式可得

同理，根据（16）式、（17）式、（23）式、（24）式和（35）式可得

根据（14）式φ定义，结合（36）式、（37）式可得

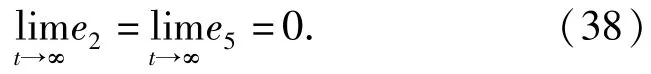
从而有

3）由（7）式、（11）式、（30）式和（39）式易得

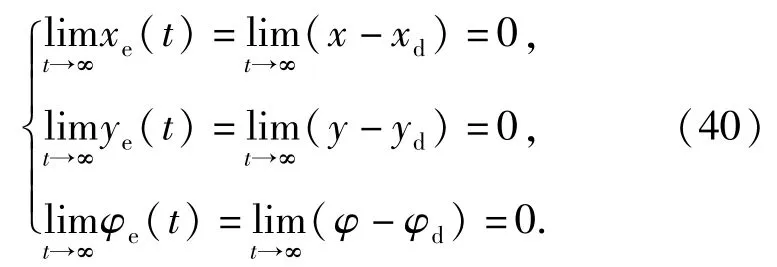
（1）式的第一个表达式可展开为

可等价变换为

由于ei（i=3，4，5，6）收敛于0，可得收敛于从而由（42）式有u、v、r收敛于则有

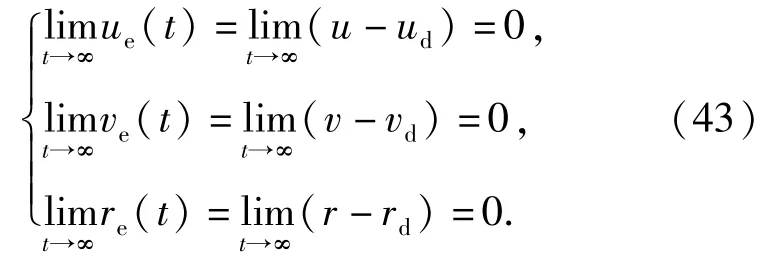
由（40）式、（43）式可知（30）式成立。定理证明完毕。

4 仿真实验

为了验证本文所提出基于非对称模型的欠驱动UMV轨迹跟踪控制方法的有效性和优越性，在实验室半物理仿真平台下进行轨迹跟踪仿真实验。所选载体见文献［8］，详细模型参数如表1所示。

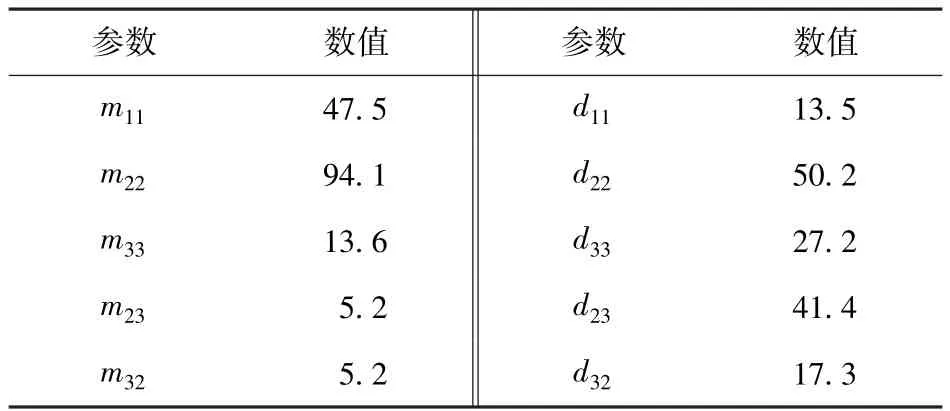
表1　UMV模型参数Tab.1 Model parameters of UMV

选择控制器参数 k1=1.5，k2=4.5，λ1=1，λ2=1，ρ1=0.5，ρ2=2，ρ3=0.5，ρ4=1，进行UMV轨迹跟踪控制仿真实验。

实验1：选择ud=5 m/s，rd=0 rad/s，期望直线轨迹由（29）式生成，选择UMV初始状态为（x（0），y（0），φ（0），u（0），v（0），r（0））=（10，10，0，0，0，0），所得结果如图2～图5所示，其中：S1表示期望轨迹，S2代表本文所提出基于非对称模型控制方法跟踪结果，S3代表传统基于对称模型控制方法跟踪结果。

图2　直线轨迹跟踪结果Fig.2 Tracking results of straight line path

图3　位姿跟踪误差Fig.3 Tracking errors of position and heading angle

实验2：选择ud=5 m/s，rd=0.1 rad/s，目标曲线轨迹由（29）式生成，选择 UMV初始状态为（x（0），y（0），φ（0），u（0），v（0），r（0））=（10，-5，0，0，0，0），所得结果如图6～图9所示。

上述采用本文所提出基于非对称模型（S2）和传统基于对称模型（S3），进行UMV直线和曲线轨迹跟踪控制仿真实验。

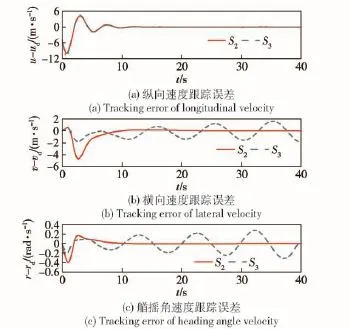
图4　速度跟踪误差Fig.4 Tracking errors of velocities

图5　UMV控制输入Fig.5 Control inputs of UMV

分析图2和图6可知：

1）在仅有纵向推进器和舵（即仅有纵向控制力τu和转艏控制力矩τr）、没有侧推进器（即不含侧向控制力τv）的欠驱动情况下，本文所提出控制方法可实现UMV的轨迹跟踪控制，控制器性能良好。

2）本文所设计的控制器，能够同时适用于直线轨迹和曲线轨迹的跟踪控制，相比文献［15-18］所设计控制器通用性更强，且本文所提出控制方法彻底地解决了角速度持续激励问题。

3）控制器设计过程中跟踪误差积分项的引入，使得轨迹跟踪过程中跟踪误差快速收敛于0，UMV迅速进入期望轨迹。

由图7的位姿跟踪误差曲线可以看出，在15 s左右，y轴方向跟踪误差y-yd发生波动，这主要是因为在y轴方向没有控制输入（即没有侧推器），y轴方向的跟踪控制是需要由x轴方向跟踪控制和艏向角跟踪控制间接实现的；而在10 s左右艏向角的跟踪控制出现了较大波动，这直接影响了x轴和y轴方向的位置跟踪控制。此外，综合分析图3～图5、图8～图9可知：

1）考虑UMV模型的非对称性，在控制器设计过程中引入非对称性影响因素，与传统的基于对称模型的控制器相比，本文所设计基于非对称模型的UMV轨迹跟踪控制器跟踪精度更高，控制稳定性更好。

2）UMV模型的非对称性因素的忽略会给控制系统带来很大误差，甚至导致轨迹跟踪控制的失败，因此在实际控制器设计过程中UMV模型非对称性是一项不可以忽略的因素。

图6　曲线轨迹跟踪结果Fig.6 Tracking results of curve path

图7　位姿跟踪误差Fig.7 Tracking errors of position and heading angle

图8　速度跟踪误差Fig.8 Tracking errors of velocities

图9　UMV控制输入Fig.9 Control inputs of UMV

5 结论

考虑UMV系统阻尼系数矩阵和惯性系数矩阵非对角线元素存在非零项的问题，本文提出了一种基于非对称模型的欠驱动UMV轨迹跟踪控制方法。基于非线性反步法的虚拟状态和输入反馈变换设计，解决了UMV轨迹跟踪过程中存在的角速度持续激励问题，设计了直线和曲线轨迹跟踪的通用控制器。引入跟踪误差积分项，提高系统跟踪误差的收敛速度，通过Barbalat引理和Lyapunov稳定性理论分析了系统的稳定性。通过进行基于本文提出非对称模型和传统对称模型的UMV轨迹跟踪对比，发现模型非对称性对系统控制性能影响较大，在控制系统设计过程中不可忽略，模型非对称性影响因素的引入能提高系统的控制精度和稳定性。实验室半物理仿真环境下进行的轨迹跟踪控制实验验证了所提出方法和所设计控制器的有效性、可靠性和优越性。

（References）

［1］ Gomariz S，Masmitja I，Gonzalez J，et al.GUANAY-II：an autonomous underwater vehicle for vertical/horizontal sampling［J］. Journal of Marine Science and Technology，2015，20（1）：81-93.

［2］ 万磊，张英浩，孙玉山，等.基于重构容错的智能水下机器人定深运动控制［J］.兵工学报，2015，36（4）：723-730. WAN Lei，ZHANG Ying-hao，SUN Yu-shan，et al.AUV’s depth control based on reconstructive fault-tolerant control［J］.Acta Armamentarii，2015，36（4）：723-730.（in Chinese）

［3］ Bonin-Font F，Oliver G，Wirth S，et al.Visual sensing for autonomous underwater exploration and intervention tasks［J］.Ocean Engineering，2015，93：25-44.

［4］ Fang M C，Wang S M，Wu M C，et al.Applying the self-tuning fuzzy control with the image detection technique on the obstacle-avoidance for autonomous underwater vehicles［J］.Ocean Engineering，2015，93：11-24.

［5］ Han J，Park J，Kim T，et al.Precision navigation and mapping under bridges with an unmanned surface vehicle［J］.Autonomous Robots，2015，38（4）：349-362.

［6］ Yang J M，Tseng C M，Tseng P S.Path planning on satellite images for unmanned surface vehicles［J］.International Journal of Naval Architecture and Ocean Engineering，2015，7（1）：87-99.

［7］ Xu Y M，Mohseni K.Bioinspired hydrodynamic force feedforward for autonomous underwater vehicle control［J］.IEEE/ASME Transactions on Mechatronics，2014，19（4）：1127-1137.

［8］ Dong Z P，Wan L，Li Y M，et al.Point stabilization for an underactuated AUV in the presence of ocean currents［J］.International Journal of Advanced Robotic Systems，2015，12：1-14，100.

［9］ Fossen T I.Handbook of marine craft hydrodynamics and motion control［M］.Hudson County，New Jersey：John Wiley&Sons，2011.

［10］ Xia G Q，Shao X C，Zhao A，et al.Adaptive neural network control with backstepping for surface ships with input dead-zone ［J］.Mathematical Problems in Engineering，2013，530162：1-9.

［11］ Chen X T，Tan W W.Tracking control of surface vessels via fault-tolerant adaptive backstepping interval type-2 fuzzy control ［J］.Ocean Engineering，2013，70：97-109.

［12］ Yang Y，Du J L，Guo C，et al.A trajectory tracking robust controller of surface vessels with disturbance uncertainties［J］.IEEE Transactions on Control Systems Technology，2014，22（4）：1511-1518.

［13］ 李晔，姜言清，张国成，等.一种基于电子海图的欠驱动AUV区域搜索方案［J］.机器人，2014，36（5）：609-618. LI Ye，JIANG Yan-qing，ZHANG Guo-cheng，et al.An underactuated AUV-oriented region search method based on electronic chart［J］.Robot，2014，36（5）：609-618.（in Chinese）

［14］ Park B S.Adaptive formation control of underactuated autonomous underwater vehicles［J］.Ocean Engineering，2015，93：1-7.

［15］ Harmouche M，Laghrouche S，Chitour Y.Global tracking for underactuated ships with bounded feedback controllers［J］.International Journal of Control，2014，87（10）：2035-2043.

［16］ Liao Y L，Su Y M，Cao J.Trajectory planning and tracking control for underactuated unmanned surface vessels［J］.Journal of Central South University，2014，21（2）：540-549.

［17］ 董早鹏，刘涛，万磊，等.基于Takagi-Sugeno模糊神经网络的欠驱动无人艇直线航迹跟踪控制［J］.仪器仪表学报，2015，36（4）：863-870. DONG Zao-peng，LIU Tao，WAN Lei，et al.Straight-path tracking control of underactuated USV based on Takagi-Sugeno fuzzy neural network［J］.Chinese Journal of Scientific Instrument，2015，36（4）：863-870.（in Chinese）

［18］ Katayama H，Aoki H.Straight-line trajectory tracking control for sampled-data underactuated ships［J］.IEEE Transactions on Control Systems Technology，2014，22（4）：1638-1645.

［19］ 万磊，张英浩，孙玉山，等.欠驱动智能水下机器人的自抗扰路径跟踪控制［J］.上海交通大学学报，2014，48（12）：1727-1731. WAN Lei，ZHANG Ying-hao，SUN Yu-shan，et al.ADRC pathfollowing control of underactuated AUVs［J］.Journal of Shanghai Jiao Tong University，2014，48（2）：1727-1731.（in Chinese）

［20］ Yang Y C，Yang K S，Chen C Y，et al.Robust trajectory control for an autonomous underwater vehicle［C］∥OCEANS 2013 MTS/IEEE Conference.Bergen，Norway：IEEE，2013.

［21］ Adhami-Mirthosseini A，Yazdanpanah J，Aguiar A P.Automatic bottom-following for underwater robotic vehicles［J］.Automatica，2014，50（8）：2155-2162.

［22］ Joe H，Kim M，Yu S C.Second-order sliding-mode controller forautonomous underwater vehicle in the presence of unknown disturbances［J］.Nonlinear Dynamics，2014，78（1）：183-196.

［23］ Liao Y L，Zhang M J，Wan L.Serret-Frenet frame based on path following control for underactuated unmanned surface vehicles with dynamic uncertainties［J］.Journal of Central South University，2015，22（1）：214-223.

［24］ 周佳加，严浙平，贾鹤鸣，等.改进规则下自适应神经网络的UUV水平面路径跟随控制［J］.中南大学学报：自然科学版，2014，45（9）：3021-3028. ZHOU Jia-jia，YAN Zhe-ping，JIA He-ming，et al.Improved pathfollowing in horizontal plane for UUV using adaptive neural network controller［J］.Journal of Central South University：Science and Technology，2014，45（9）：3021-3028.（in Chinese）

［25］ 张国庆，张显库，关巍.欠驱动船舶简捷鲁棒自适应路径跟踪控制［J］.哈尔滨工程大学学报，2014，35（9）：1053-1059. ZHANG Guo-qing，ZHANG Xian-ku，GUAN Wei.Concise robust adaptive path-following control for underactuated ships［J］. Journal of Harbin Engineering University，2014，35（9）：1053-1059.（in Chinese）

［26］ Miao B B，Li T S，Luo W L.A DSC and MLP based robust adaptive NN tracking control for underwater vehicle［J］.Neurocomputing，2013，111：184-189.

［27］ 万磊，董早鹏，李岳明，等.非完全对称欠驱动无人艇全局渐近镇定控制［J］.华中科技大学学报：自然科学版，2014，42（8）：48-53. WAN Lei，DONG Zao-peng，LI Yue-ming，et al.Global asymptotic stabilization control of incomplete symmetry underactuated USV［J］.Journal of Huazhong University of Science&Technology：Natural Science Edition，2014，42（8）：48-53.（in Chinese）

［28］ 万磊，董早鹏，李岳明，等.非完全对称欠驱动高速无人艇轨迹跟踪控制［J］.电机与控制学报，2014，18（10）：95-103. WAN Lei，DONG Zao-peng，LI Yue-ming，et al.Trajectory tracking control of incomplete symmetry underactuated USV at high speed［J］.Electric Machines and Control，2014，18（10）：95-103.（in Chinese）

［29］ Isidori A.Nonlinear control systems［M］.London：Springer-Verlag，1995.

Trajectory Tracking Control of an Underactuated Unmanned Marine Vehicle Based on Asymmetric Model

DONG Zao-peng1，2，WAN Lei1，2，SUN Yu-shan1，2，LIU Tao1，LI Yue-ming1，2，ZHANG Guo-cheng1，2
（1.Science and Technology on Underwater Vehicle Laboratory，Harbin Engineering University，Harbin 150001，Heilongjiang，China；2.College of Shipbuilding Engineering，Harbin Engineering University，Harbin 150001，Heilongjiang，China）

Trajectory tracking control problem of an underactuated unmanned marine vehicle（UMV）is addressed，and an integral backstepping control method based on asymmetric model is proposed.A horizontal motion model of incomplete symmetry underactuated UMV with port/starboard symmetry and without fore/aft symmetry is established，in which the off-diagonal elements of damping coefficient matrix and inertia coefficient matrix are considered to be non-zero.A feedback transformation of virtual state and control input is designed to relax the well-known persistent exciting conditions of yaw velocity in trajectorytracking control of UMV，and then a general trajectory tracking controller for both straight line path and curve path is obtained.The global stable convergence rate of UMV system is improved by introducing an integral item of tracking errors into trajectory tracking controller.The stability of the system is proved by Lyapunov theory and Barbalat’s lemma.With the help of the semi physical simulation platform，the advantages of the asymmetric model-based underactuated UMV trajectory tracking control method proposed in this paper is demonstrated in simulation experiments by comparing with the traditional symmetric model-based method.

control science and technology；unmanned marine vehicle；asymmetric model；underactuated control；trajectory tracking；integral backstepping method

TP273

A

1000-1093（2016）03-0471-11

10.3969/j.issn.1000-1093.2016.03.012

2015-07-29

国家“863”计划项目（2012AA09A304）；国家自然科学基金项目（51409054、51409059、51409061、51509057）

董早鹏（1988—），男，博士研究生。E-mail：dongzaopeng@hrbeu.edu.cn；万磊（1964—），男，研究员。E-mail：wanlei@hrbeu.edu.cn