有限维Hilbert空间中紧框架的构造
林玉珍, 朱玉灿
(福州大学数学与计算机科学学院, 福建 福州 350116)
有限维Hilbert空间中紧框架的构造
林玉珍, 朱玉灿
(福州大学数学与计算机科学学院, 福建 福州350116)
讨论了R2上单位模紧框架的一些性质, 以及R2上的单位模紧框架上可执行(r,k)手术的一个充要条件. 最后推广了R2上的单位模紧框架可执行((a-1)·(k+u),k)手术的条件, 并举例说明.
框架; 紧框架; 图向量; 框架手术
0 引言
1952年, Duffin等[1]在研究非调和Fourier级数问题时引入框架的概念. 目前, 框架理论是一个应用广泛的研究方向, 而对有限维空间上的框架的研究已经引起越来越多国内外学者的重视, 并取得了一系列重要的研究成果[2-3].
由于紧框架在许多实际问题诸如信号处理中有非常重要的应用, 因此越来越多的人重视对紧框架的研究[3-8]. 跟一般框架相比, 紧框架的重构公式比较简单, 紧框架能避免在框架重构时框架算子的逆算子不容易计算、 运算量大的麻烦. 所以在实际应用时需要构造一些紧框架. 文献[9]给出构造紧框架的一种方法, 即由一个Bessel序列通过添加一些向量后使它构成紧框架, 而文献[10]给出构造紧框架的另一种方法, 即先去除原框架中的一些向量后再添加一些向量使它构成一个新的紧框架.

首先简要介绍框架的一些基本概念和性质.
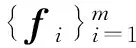
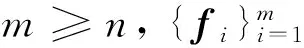
一个紧框架可执行(r,k)手术是指在去除紧框架里r个向量的同时再添加k个向量后仍是紧框架. 文献[10]得到R2的单位模紧框架可执行(r,k)手术的一个充要条件如下.
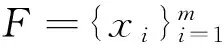

定理1得到R2的单位模紧框架在任意正整数k下可执行(r,k)手术的一个充要条件, 但事实上在k=1时是不成立的(见例1), 对定理1进行适当的改正, 并且给出详细的证明. 讨论正整数a和u满足一定的条件, 都可在去除(a-1)·(k+u)个向量的同时只需再添加k个单位模向量后得到的一个新的还是单位模紧框架. 这种方法可以在构造新的单位模紧框架时有更多的选择性, 并且可以在添加的向量个数一样的前提下去除更多的向量后还构成新的单位模紧框架, 使得新的单位模紧框架的向量个数可以更少.
1 主要结论
下面给出k=1时定理1不成立的例子.


定理1的原证明过程太过简略, 下面对k>1的情况进行详细的证明.
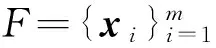
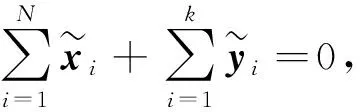
又由于
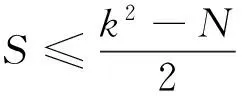
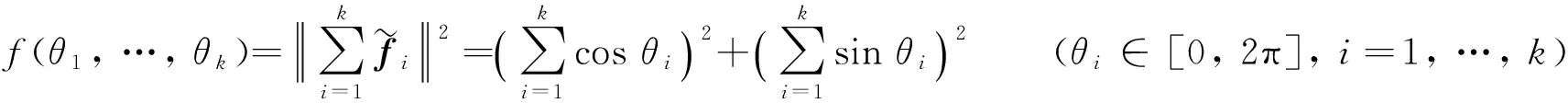

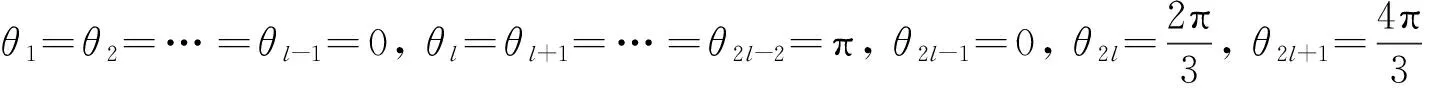
则
所以,f(θ1,θ2, …,θk)可以取得到0.
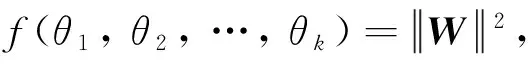
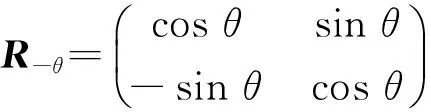
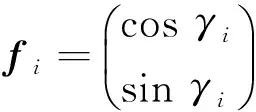

所以由定理3可知存在一个((a-1)·(k+u),k)手术, 使得其构成R2的一个新的单位模紧框架.

表1 新框架的向量个数分布Tab.1 The distribution of the number of vectors for a new frame
定理3讨论的是在k>1的情况下, 可以执行(r, k)手术的一个充要条件. 以下是在k=1的情况下, 可以执行(r, 1)手术的一个充要条件.

[1]DUFFINRJ,SCHAEFFERAC.AclassofnonharmonicFourierseries[J].TransAmerMathSoc, 1952, 72: 341-366.
[2]CASAZZAPG,KUTYNIOKKG.Finiteframes:theoryandapplications[M].Boston:BostonBirkhauser, 2012.
[3]CHRISTENSENO.Framesandbases:anintroductorycourse[M].Boston:BostonBirkhauser, 2008.
[4]CASAZZAPG,LEONMT.Existenceandconstructionoffinitetightframes[J].JConcrApplMath, 2006, 4(3): 277-289.
[5]CASAZZAPG,FICKUSM,MIXONDG.Constructingtightfusionframes[J].ApplComputHarmonAnal, 2011, 30(2): 175-187.
[6]BENEDETTOJJ,FICKUSM.Finitenormalizedtightframes[J].AdvComputMath, 2003, 18(2/3/4): 357-385.
[7]CASAZZAPG,FICKUSM,KOVACEVICJ.Aphysicalinterpretationoftightframes[M].Boston:BostonBirkhauser, 2006: 51-76.
[8]CASAZZAPG,KOVACEVICJ.Equal-normtightframeswitherasures[J].AdvComputMath, 2003, 18(2/3/4): 387-430.
[9]LIDF,SUNWC.Expansionofframestotightframes[J].ActaMathematicaSinica:EnglishSeries, 2009, 25(2): 287-292.
[10]NARAYANSK,RADZWIONEL,RIMERSP.Robustnessandsurgeryofframes[J].LinearAlgebraAppl, 2011, 434(8): 1 893-1 901.
[11]COPENHAVERMS,KIMYH,LOGANC,etal. Maximum robustness and surgery of frames in finite dimensions[J]. Linear Algebra Appl, 2013, 439(5): 1 330-1 339.
(责任编辑: 洪江星)
Constructing tight frames in finite dimensional Hilbert spaces
LIN Yuzhen, ZHU Yucan
(College of Mathematics and Computer Science, Fuzhou University, Fuzhou, Fujian 350116, China)
We discuss some properties of unit-norm tight frames in R2, and give a necessary and sufficient condition for an (r,k)-surgery on unit-norm tight frames in R2. Finally, we generalize the condition under which a unit-norm tight frame can carry on the ((a-1)·(k+u),k)-surgery, and give an example to illustrate it.
frame; tight frame; diagram vector; frame surgery
10.7631/issn.1000-2243.2016.01.0001
1000-2243(2016)01-0001-05
2013-05-31
朱玉灿(1963-), 教授, 主要从事框架理论及其应用、 多复变函数几何理论、 几何函数论研究,zhuyucan@fzu.edu.cn
福建省自然科学基金资助项目(2012J01005); 国家自然科学基金资助项目(11226099)
O177.1
A

