基于Remington模型的列车滚动声模型

张琪　刘妞　刘畅

(广西科技大学　电气与信息工程学院, 广西柳州　545006)



基于Remington模型的列车滚动声模型

张琪刘妞刘畅

(广西科技大学电气与信息工程学院, 广西柳州545006)

列车滚动声是列车运行时产生的噪声最主要的组成部分，要深入研究它需先建立相应的数学模型。Remington模型是应用最广泛的一种滚动声模型，在Remington模型的基础上将轮轨振动分为垂向的Euler梁振动和横向的棒振动，并分别对这两种振动展开分析。通过一些基本的列车轨道参数各自求出它们的一阶特征频率和二阶特征频率，最后对比这两组数据，得出钢轨在低频段振动特点。

滚动声模型；垂向振动；横向振动；特征频率

铁路运输是我国国民经济的大动脉,铁路高速发展给我们出行带来便捷的同时，列车运行时产生的噪声也给人们带来很多不必要的麻烦。研究表明列车运行时产生的噪声中，列车运行轮轨噪声占的比例最大，轮轨噪声主要分为冲击声、尖啸声、滚动声三种类型[1]：冲击声主要是由于车轮在通过钢轨与钢轨接头凸出处、道岔以及擦伤后的车轮在钢轨上滚动产生的；尖啸声主要是由列车尤其是大吨位的货运列车通过小曲率半径(转弯)的列车线路时,车轮边缘挤压外轨以及内侧车轮踏面在钢轨上滑动产生的；滚动声则主要是因为钢轨接触表面有微小和不可避免的凸凹不平(即钢轨的表面粗糙度),当车轮在粗糙表面的钢轨上滚动时,遇到这些小的凸起部分或者凹槽部分时,必然会引起车轮和钢轨的振动,同时产生滚动噪声[2]。随着铁路技术的高速发展，无缝钢轨技术在我国铁路线路中大面积使用，钢轨需要接头的数量大大减少了，同时修建的铁路线路的曲线半径也大大增大，列车运行时产生的尖啸声和击噪声基本上得到了控制。现在技术还无法保证钢轨表面绝对光滑，因此滚动噪声成为如何降低轮轨噪声的重点。国内外建立了各种滚动声模型，其中Remington教授建立的轮轨噪声模型,被认为是最全面的轮轨振动及噪声分析模型[3]。在Remington模型的基础下，将列车滚动声的产生的原因归为是钢轨的垂向振动和横向振动共同作用的效果，并分建立垂向振动模型和横向振动模型。

1　列车车轮与钢轨间的作用力

声音是由振动产生的，列车运行时轮轨与钢轨之间的作用力使车轮和钢轨振动，这种作用力十分复杂，为方便研究，Remington模型将行驶中列车车轮作用在钢轨上的力，分解成为垂直于钢轨的横向水平力和平行于钢轨的纵向水平力等三个分力[4](如图1所示)。在垂向分力Fy的作用下,钢轨有沿着垂向方向的振动；横向分力Fz使得车轮轮缘与钢轨内侧面发生摩擦挤压作用，钢轨在这种挤压力作用下横向振动；而纵向分力Fx成为列车行驶中牵引力的一部分。

2　钢轨的垂向振动

列车运行时钢轨横向振动产生的轮轨滚动噪声，不仅是由某单个车轮对某段钢轨随机振动产生的，而是整列车所有的车轮及其对应的一段轨道的振动所产生的整体作用的结果[5]。简化受力分析模型(如图2所示)，其中，虚线框模拟一辆每节车厢长度为lt，以速度v向前移动的列车，pi为车轮对钢轨的作用力，Frsi(i=1，…，N)是轮轨支点反力，N为长度l范围内轨枕支点总数，ox为固定于钢轨的固定坐标系，o′x′是连接车辆的移动坐标系。

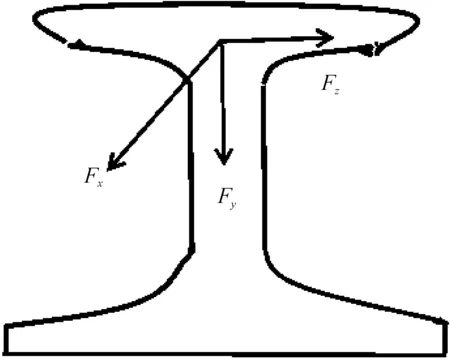
图1　列车运行时车轮与钢轨的作用力

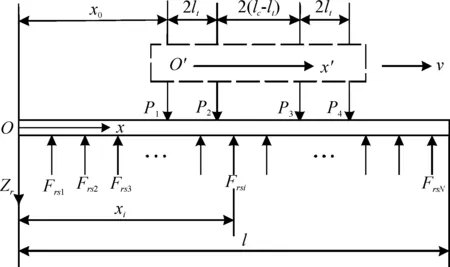
图2　垂向振动钢轨受力分析图

将此钢轨垂向振动简化为一个Euler梁模型，根据 D’Alembert 原理，获得钢体构件的二阶振动微分方程[6]。设钢轨的振动位移为zr(x,t)，钢轨弹性模量为E，截面惯量为I，其振动微分方程为：

(1)

(2)

式中：Zr(xi,t)为枕木的垂向振动位移，K(p)为轮轨下胶垫阻尼，C(p)轮轨下胶垫钢度。

方程(1)是一个四阶偏微分方程，为了方便对方程进行数值分析，引入一个正则坐标即正则振型函数qk(t)，将此四阶偏微分方程函数转化为一个二阶常微分方程组，应用简支梁的正则振型函数，令Zsi(t)=Zsi(t)=0，可以求得钢轨振动的各阶特征频率，其中一阶特征频率150 Hz，二阶频率为305 Hz。

3　钢轨的横向振动

钢轨在横向分力的作用下，使钢轨在该方向上横向振动，由于枕木扣件将钢轨固定在枕木上，可以将钢轨看作一段段两端固定的棒的振动[7-8]，如图3所示。

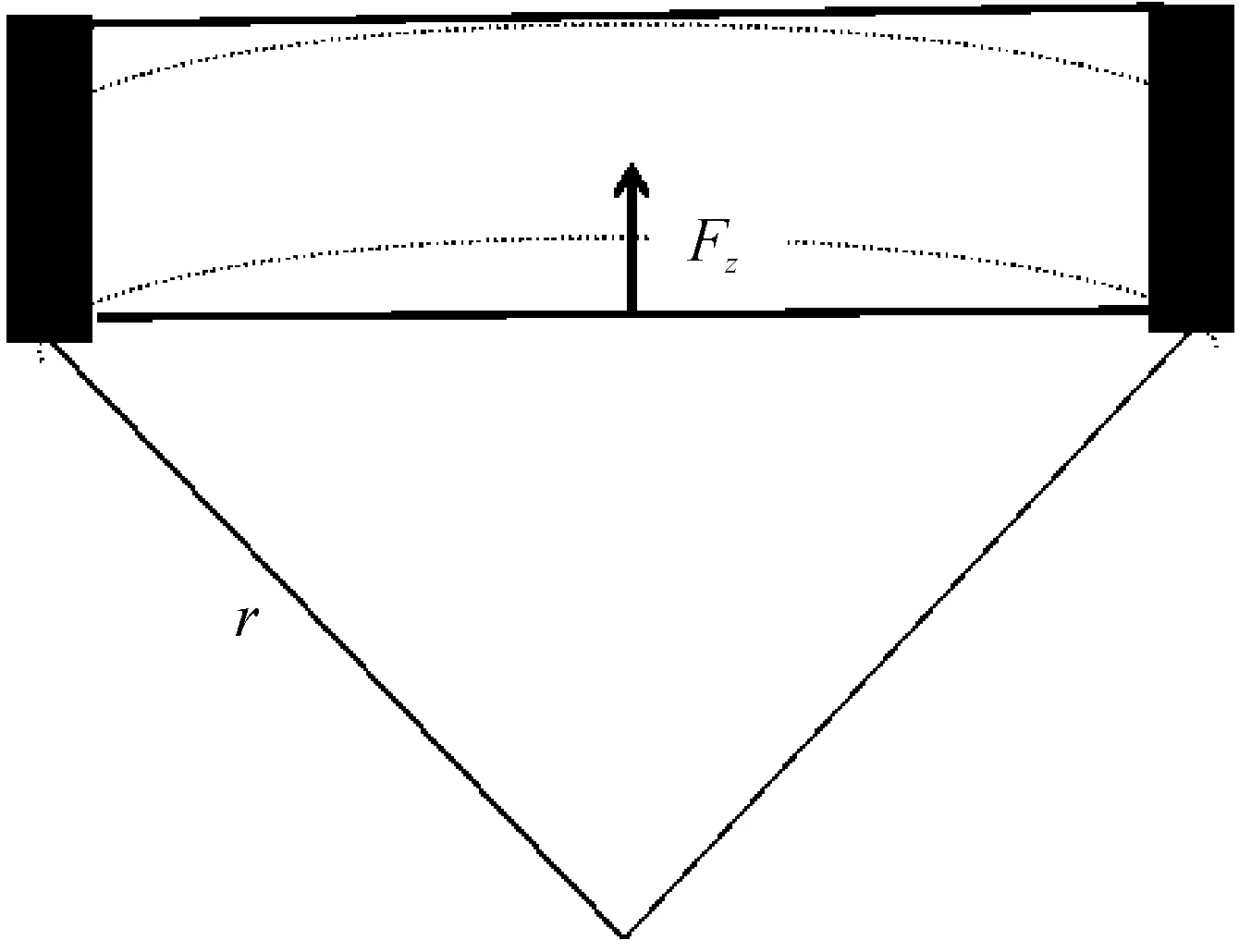
图3　横向振动钢轨受力分析图

根据棒振动的特点[9]，可以得到棒的横振动方程为：

(3)

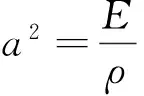
(4)

钢轨在横向振动频率可以用以下方程来计算

(5)

以我国铁路钢轨普遍采用的60 kg/m标准钢轨为例[11],钢轨与枕木之间的距离大约为d=0.54m，声音在钢轨中的传播速度c=5 050m/s，轨道参考回转半径k=5.7×10-3m，最后将频率阶数n代入计算可得一阶特征频率f1=155Hz,二阶特征频率f2=310Hz。

4　结语

讨论钢轨在Remington滚动声模型基础上，将由轮轨激励力作用产生的滚动声，分为钢轨的垂向振动和横向振动。对于轮轨激励力作用下的垂向振动分析，将钢轨垂向振动简化为Euler梁模型模型，通过降阶、数值仿真等方法，获得了60 kg/m的钢轨振动的特征频率值(一阶特征频率大约是150 Hz，二阶特征频率大约是305 Hz)。分析钢轨横向振动时，将钢轨简单成两端固定的棒振动模型，根据的60 kg/m钢轨的回转半径的大小计算了钢轨横向振动的特征频率值(一阶特征频率大约是155 Hz，二阶特征频率大约是310 Hz)，二者数据符合度较好，说明钢轨在低频段的振动形式是整体振动。

[1]熊芯.列车滚动噪声的仿真分析研究[D].北京：铁道部科学研究院,2002.

[2]刘正平,程蔚,冯召勇,等.基于轮轨噪声检测的列车接近报警研究[J]. 机械设计与制造, 2011, 4(4):1-3.

[3]Remington P J.Wheel/Rail rolling noise I:Theoretical Analysis[J].J Acoust Soe A M，1987,81(6):1805-1821.

[4]杨清雷,傅圣雪,王泽华.基于固体声检测的列车接近报警系统 [J]. 青岛科技大学学报，2005, 26(6): 1-3.

[5]韩光旭.高速列车车轮非圆化对振动噪声的影响及演变规律研究[D].成都：西南交通大学，2015.

[6]韩军.铁路轮轨系统中轮辐结构式与振动噪声关系的分析研究[D].大连：大连铁道学院，1999.

[7]万淑敏.铁路钢轨振动与声辐射分析与控制[D]. 上海：上海交通大学，2009.

[8]Remington P J.Wheel/rail Rolling noise:what do we know?don’t we know Where are we go from here?[J]. Journal of Noise and Vibration，1988, 120(2): 203-226.

[9]孙月明,唐任仲.机械振动学[M].杭州:浙江大学出版社,1999.

[10]刘晓波,刘剑.LEVanbration.轨道列车振动与噪声研究现状与发展[J]. 电力机车与城轨车辆，2013(6): 12-18.

[11]黄婧.列车车轮振动与声辐射仿真分析[D].南昌：华东交通大学，2004.

Rail Rolling Noise Model Based on Remington Model

ZHANG QiLIU NiuLIU Chang

(Electrial and Information Engineering Academy, Guangxi University of Science and Technology, Liuzhou 545006, China)

Rail rolling noise as an important role in train running noise, is needed to establish its mathematical model. On the basis of Remington model, the most widely used in all kinds of rail rolling noise model, the rail rolling is divided into Vertical Euler vibration and Transverse steel vibration, so that some basic rail parameters can be made into the first-order and second-order characteristic frequency. Finally, comparing the two groups of data obtains the characteristics of rail in low frequency vibration.

rolling noise model; vertical vibration; transverse vibration; characteristic frequency

2015-12-23

张琪(1990—)，男，安徽安庆人，硕士生，主要从事智能控制及应用研究。

TP183

A

1009-0312(2016)03-0024-03