电磁场散度概念的形象化教学

何思远　朱艳（武汉大学 电子信息学院，湖北 武汉 430072）

电磁场散度概念的形象化教学

何思远朱艳
（武汉大学 电子信息学院，湖北 武汉 430072）

矢量场的散度是描述矢量场空间分布和变化规律的有力工具，同时也是电磁场理论中理解麦克斯韦方程的重要基础。但是由于散度概念性强、描述抽象，初学者难以掌握而畏难。文章在教学过程中，首先介绍了描述矢量场的另外两个更形象和具体的方法，即矢量线和通量。文中详细讨论了矢量线，通量和散度三种描述方法的联系和区别，指出他们各自的优点和不足，将散度的概念建立在前面两种方法的基础之上。从矢量线和通量对矢量场形象化的具体描述再过渡到散度对矢量场的抽象描述，文章的教学方法由浅入深、由易转难。同时在教学过程中将数学形式和物理含义紧密联系，可以帮助学生建立起正确的概念图像。

散度；矢量场；通量抗

引言

麦克斯韦方程是宏观电磁场的核心理论。矢量场的散度是描述矢量场空间分布和变化规律的有力工具，同时也是理解麦克斯韦方程的重要基础。但是由于散度的定义涉及求极限，散度的运算包含偏微分，散度作为数学概念非常难以理解，散度对矢量场的描述特别抽象，初学者通常很难掌握而对电磁场理论这门课程产生畏难。针对这一问题，在散度教学过程中，首先介绍了描述矢量场的另外两种更形象和具体的方法，即矢量线和通量的概念，并且借助于矢量线和水流线，通量和水流流量，通量源和水源等具体概念的类比，帮助学生理解通量的物理含义。文中详细讨论了矢量线，通量和散度三种描述方法的联系和区别，指出他们各自的优点和不足，将散度的概念建立在前面两种方法的基础之上。从矢量线和通量对矢量场形象化的描述过渡到散度对矢量场的抽象描述，由浅入深，由易转难，文章的教学方法可以让学生更好的理解和掌握散度的概念。同时文章也将数学形式和物理概念紧密联系，帮助学生建立起正确的概念图像。

一、矢量场与矢量线

矢量场是空间某个区域上既有大小又有方向的物理量，如电场强度、磁场强度、力场、流速场等。矢量线是描述矢量场大小和方向的有向曲线，如描述电场和磁场的电力线与磁力线都是学生非常熟悉的图像。矢量场的强度由矢量线的疏密程度描述，线越密则场值越大，线越疏则场值越小。矢量场的方向由矢量线上每一点的切向方向给出。矢量线对矢量场的描述非常形象，初学者比较容易理解。但是矢量线只能定性描述矢量场，不能定量描述。定量化是我们科学研究的重要方法，因此我们需要引入通量的概念。

二、矢量场的通量

通量是定义在空间一定场区域上，我们先讨论矢量场对于一个无限小面元的通量。矢量场对于任意曲面的通量为曲面上所有小面积元通量的叠加。

在矢量场分布区域任取一个面元ds，穿过该面元的矢量线的总数称为矢量场对于该面元的通量。用数学式来表述其定义:

可以看出矢量场的通量是一个标量，影响其大小的关键因素有两个：第一，通量的值和面元的法向有关。当面元法向和矢量场垂直时通量为零。当面元法向和矢量场平行时，通量取最大。第二，通量的值和单位面积的矢量线数目有关。当面元法向和矢量场平行时，单位面积的矢量线数目表征了矢量线疏密程度，由该点处的矢量场值决定。那么当面元法向和矢量场有夹角时，矢量场垂直穿过面元的分量才是计算通量的有效分量。

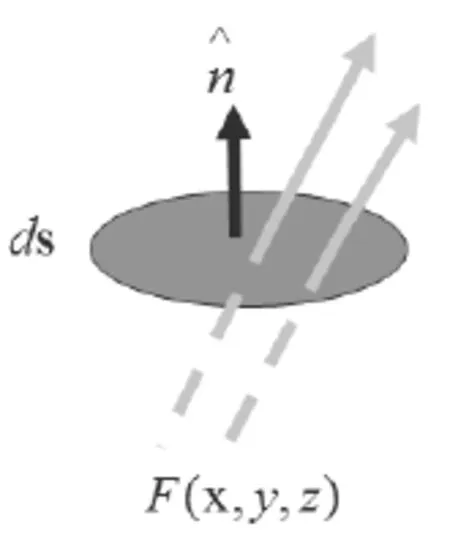
图1　面元法向与矢量场方向

为了便于学生加深对通量的理解，将通量和流量作类比，那么矢量线就对应水流线，矢量场就对应流速场。流量的计算公式就和通量的计算公式非常相似：

从对物理量的单位进行分析可以得出为什么等式左边是流量。流速的单位是米每秒，面积的单位是平方米，相乘得到立方每秒，也就是流量的单位。

为了引出通量源的概念，我们需要讨论闭合曲面的通量。那么什么是通量源呢？通量和通量源是什么关系呢？也可以借助于流量的例子来理解。闭合曲面有水流流出，闭合曲面的流量大于零时，很自然会问，水流是从哪里来的？这个问题也可以借助古诗形象提问：问渠哪得清如许？答案就是，为有源头活水来！也就是说闭合曲面包围区域产生水流的能力来自于内部存在的水源。通量源就类似于水源。水源越强，流量越大。因此，通量和通量源成正比。闭合曲面的通量定量反映了闭合曲面内部激励矢量场的能力，这种能力来自于闭合曲面内部的通量源。通量源有三种情况。当通量大于零，表明该区域有净的矢量线流出，具备发散矢量线的能力，区域内部对应一个正源。这个现象也有古诗为其描述：泉眼无声惜细流。当通量小于零，表明该区域有净的矢量线流入，具备汇聚矢量线的能力，区域内部对应一个负源，比如一个蓄水池或者大海。当通量等于零，表明该区域内部无源，或者流进的矢量线等于流出的矢量线。

为了进一步理解通量源，以图2电力线分布为例，具体讨论电场的通量源。穿过黑色虚线所包围的闭合曲面的矢量线数目大于零，电场通量大于零，那么意味着区域内部有一个正源，也就是正电荷。同理，电场针对闭合曲面通量小于零时，区域内部对应一个负源，也就是负电荷。闭合区域通量为零时区域内部无源。

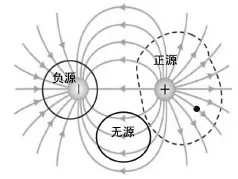
图2　电力线分布图

闭合曲面的通量从宏观上建立了矢量场和源的关系。从通量的值，可以反映出闭合曲面内部源的大小，但是并不能判断出源的位置具体在哪里？通量的值描述了闭合曲面包围区域激励起矢量场的能力，但是不能描述区域内部具体某一点上具备的激励场的能力。因此，为了定量研究一点的场和一点的源的关系，要引入散度的概念。

三、矢量场的散度

矢量场在一点的散度，定义为矢量场通过包含该点在内的任意闭合小曲面的通量与曲面元体积之比的极限，并记做div F，其数学表达式如下：

散度建立在通量的基础上，散度和通量有联系又有区别。通量是描述一个大的区域上，具备的激励矢量场的能力，是一个积分量。散度是描述一点上，具备的激励矢量场的能力，是一个微分量。

由于散度的定义涉及的体积求极限非常抽象，通常也是学生理解的难点。在作者的教学过程中，借助于PPT动画给学生们展示了体积求极限趋近于一点的动态过程，帮助学生理解从通量到散度的过渡。

理解散度的定义，还要注意对闭合曲面选取的任意性。闭合曲面的选取可以按照计算简易的原则来取。通过在直角坐标系下选取平行六面体导出散度计算的简洁公式，

散度的性质有三条。第一、由散度的定义可知，散度表示在一点处单位体积内散发出来的矢量场的通量，所以散度具有矢量场通量体密度的量纲，在空间内构成一个标量场。二、矢量场的散度反应了空间各点的净通量状态。若div F> 0，则该点有发出矢量线的正通量源。若div F<0，则该点具有汇聚矢量线的负通量源；若divF=0，则该点无通量源。第三、散度与源的关系：矢量场相对于小体积元的通量与通量源成正比。已知

其中p（x，y，z）为通量源密度，k为比例常数，通常由实验获得。结合散度的定义可得：

四、结束语

矢量线、通量、散度是描述矢量场空间分布和变化规律的三种方法。文章详细讨论了矢量线，通量和散度三种描述方法的联系和区别，指出他们各自的优点和不足。教学过程中通过与具体水流流量、水源等概念的类比，阐述了通量与通量源的联系。并将散度的概念建立在通量的基础上，通过PPT动画演示了由通量到散度求极限的过程，帮助学生更好的理解物理概念。文章由浅入深、由易转难、逐层递进的教学方法在教学实践中获得了有效的教学效果。

［1］Jin Au Kong.电磁波理论.第四版［M］.吴季，等译.北京:电子工业出版社，2003.

［2］毕德显.电磁场理论［M］.电子工业出版社，1985.

［3］谢处方，饶克谨.电磁场与电磁波.第四版［M］.高等教育出版社，2007.

［4］孙玉发.电磁场与电磁波［M］.合肥工业大学出版社，2006.

The divergence of vector field is a powerful tool to describe the spatial distribution and variation law of vector field.It is also an important foundation for understanding the Maxwell equation in the theory of electromagnetic field.But because the concept of divergence is strong，it is so difficult to grasp the abstract description that beginners fear.In this paper，it firstly describes the other two more vivid and specific methods of the vector field in the teaching process，namely，vector line and flux.In this paper，the relations and differences between three methods are discussed in detail，and it points out their respective advantages and disadvantages.The concept of divergence is established on the basis of the previous two methods.It reflects the transition that from the specific description of vector line and flux of vector field visualization to abstract description of the divergence to vector field.The paper adopts the method of from the shallower to the deeper.At the same time，the mathematical form and physical concepts are closely linked.It can help students understand the physical meaning of divergence and establish the correct concept of image.

divergence；vector field；flux resistance

G642

A

2096-000X（2016）17-0113-02

何思远（1982-），女，博士，副教授，从事电磁场理论的教学研究工作。