一种交叠的Shuffled-BP LDPC译码算法

范亚楠 王丽冲 姚秀娟 孟 新



一种交叠的Shuffled-BP LDPC译码算法

范亚楠*①②王丽冲①②姚秀娟①孟 新①

①(中国科学院国家空间科学中心 北京 100190)②(中国科学院大学 北京 100190)

Shuffled-BP(SBP) 译码算法是一种基于变量节点的串行消息传递译码算法，其收敛速度快于原有的置信度传播译码算法，然而由于实际工程实现中的半并行化处理，其收敛速度和误码性能均有所降低。为了进一步提高SBP算法的性能，该文提出一种交叠的Shuffled-BP(Overlapped Shuffled-BP, OSBP)译码算法。该算法采用若干个相同的子译码器以不同的更新顺序同时进行更新，对于每个变量节点，在每次迭代更新后选取最可靠的信息参与下一次迭代，以此提高迭代的收敛速度。理论分析和仿真实验均表明，在不增加额外存储空间的条件下，OSBP算法相比于SBP算法有着更优的误码性能以及更快的收敛速度。此外，提出的OSBP算法对于规则和不规则LDPC码均有效。

LDPC码；收敛速度；译码算法；Shuffled-BP；交叠的Shuffled-BP

1 引言

LDPC码以其渐进香农限[1,2]的误码性能而被信道编码界所广泛关注。由于其校验矩阵的稀疏性，其译码算法的空间复杂度较低，并且相比于Turbo码有着更低的错误平台。1962年，Gallager在其博士论文[3]里提出了置信度传播(Belief-Propagation, BP)LDPC译码算法，BP算法是一种基于洪水消息传递机制的译码算法，其收敛速度慢，并且消耗的计算资源和存储资源均非常巨大。为弥补BP算法的不足，研究人员开始研究基于串行消息传递机制的译码算法，例如文献[4,5]中提出的分层译码算法以及文献[6,7]中提出的Shuffled-BP(SBP)译码算法。在该类算法中，消息逐节点依次进行更新和传递，这样使得在一次迭代中刚更新过的消息立刻参与到本次迭代的其他消息的更新中去，因而获得了较BP算法近两倍的收敛速度。另外，基于SISO的实现方式又节省了大量的存储空间，同时降低了计算复杂度。

由于SBP算法串行更新的缘故，其译码延时比较大。为了降低译码延时，实际工程应用中一般需要进行半并行化处理，如文献[8,9]中所做的那样。然而并行处理后，各组中更新的信息并没有被该组其他节点所利用，导致SBP算法的收敛速度和误码性能均有所降低。为了进一步提升SBP算法的性能，文献[10]通过按变量节点度数递减的顺序进行更新，来加快SBP算法的收敛速度，但是该方法只适用于非规则LDPC码，对于规则LDPC码并没有效果；文献[11,12]引入了残差幅度(Residual Magnitude, RM)的概念，每次迭代时选择RM最大的节点进行更新，以此来提高SBP算法的收敛速度和误码性能，但是由于该算法每次迭代都要计算RM，计算复杂度相当巨大，在实际工程中并不适用。

鉴于此，本文针对SBP算法提出了一种交叠的Shuffled-BP(OSBP)算法，该算法充分利用SBP算法的特点，将若干个相同的子译码器以不同的顺序同时进行译码。每次迭代后，保留更可靠的变量节点信息参与判决和下一次迭代，进而使得判决更可靠。最终提出的算法在不增加额外存储空间的条件下，使得SBP算法的误码性能和收敛速度均有明显的提升，并且该算法对于规则和非规则LDPC码均有效。

本文以下的结构如下：第2节介绍SBP译码算法以及该算法的特点；第3节在第2节的基础上引出了该文提出的交叠的Shuffled-BP算法，并详细介绍了子译码器偏移量和更新顺序的选取；第4节利用高斯近似的密度进化对OSBP算法的收敛性进行了理论分析；第5节分别对于规则和不规则LDPC码给出了相应的仿真结果；第6节对全文进行了总结。

2 Shuffled-BP(SBP)算法的基本原理

Zhang和Fossorier在文献[6]中提出的SBP算法是概念层面的描述，并没有考虑其具体的实现方式。SBP算法在实际应用中是一种基于SISO的迭代译码算法，本文以此方式对SBP算法进行描述，以便于解释后续本文的算法，同时这样的描述也可以给实际工程实现提供理论依据。

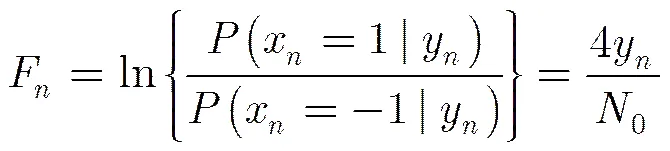
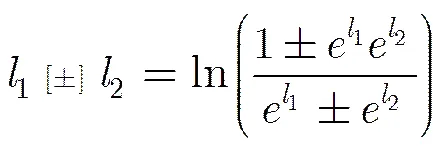
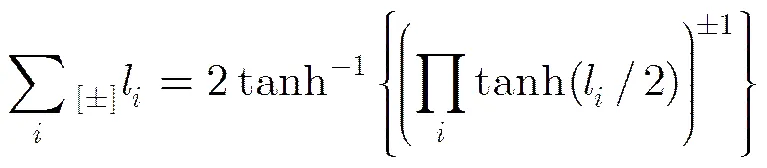
下面给出SBP算法的具体步骤：

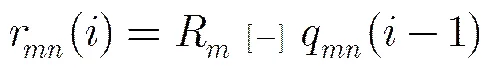
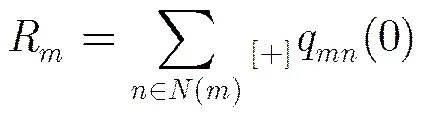
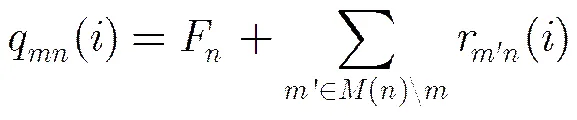
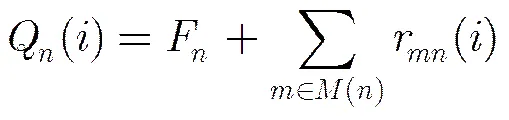
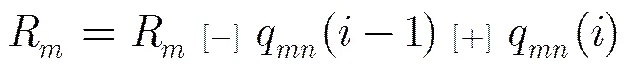
在实际工程实现中，SBP算法可以方便地进行并行处理：设并行度为，变量节点平均分成组，每组个节点，每组各节点并行更行，而不同组之间串行更新，此时在第1步中，对于，每个，以及，式(8)应变为

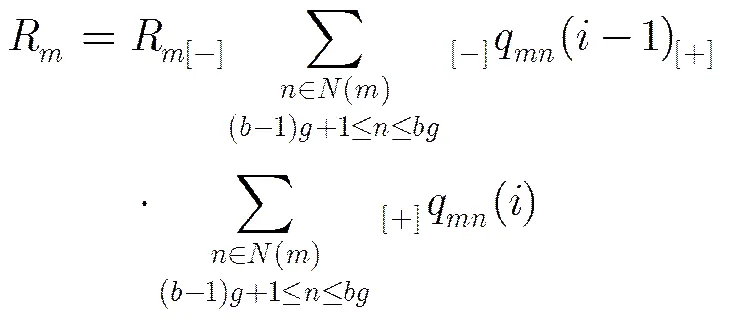
由于SBP算法是逐变量节点依次进行更新的，所以每列更新的时间不同。列更新的时间越晚，则有越多的更新后的信息参与到该列的更新中去，从而得到的变量节点信息更可靠。如果按升序的顺序进行更新，则越大，对应的变量节点信息越可靠，错误率越低；相应地，如果按降序的顺序进行更新，则越大，对应的变量节点信息越不可靠，错误率越高。

图1表示了在信噪比为3.0 dB时，通过对10000帧(192,96)(3,6)规则LDPC码编码数据分别采用升序与降序SBP算法进行仿真，得到的不同比特位置的错误比特数。从图中可以看出越晚更新的变量节点，节点的错误比特数越少，其对应的信息越可靠，错误率越低。如果将多个相同的子译码器以不同的节点顺序同时进行迭代，每次迭代后，针对于每一个变量节点在各个子译码器中选取最可靠的信息进入到下一次迭代，从而提高判决的可靠性以及译码器的收敛速度。基于此，本文提出了交叠的Shuffled- BP算法。

3 交叠的Shuffled-BP(OSBP)译码算法

正如第2节分析的那样，SBP算法中变量节点信息的可靠性随更新时间增加而提升，为了充分利用可靠度更高的信息，利用多个子译码器以不同的更新顺序同时进行译码。在每次迭代过程中，各子译码器生成并相互之间传递更可靠的信息，从而提高判决的正确率和译码收敛速度，这就是OSBP算法的基本思想。

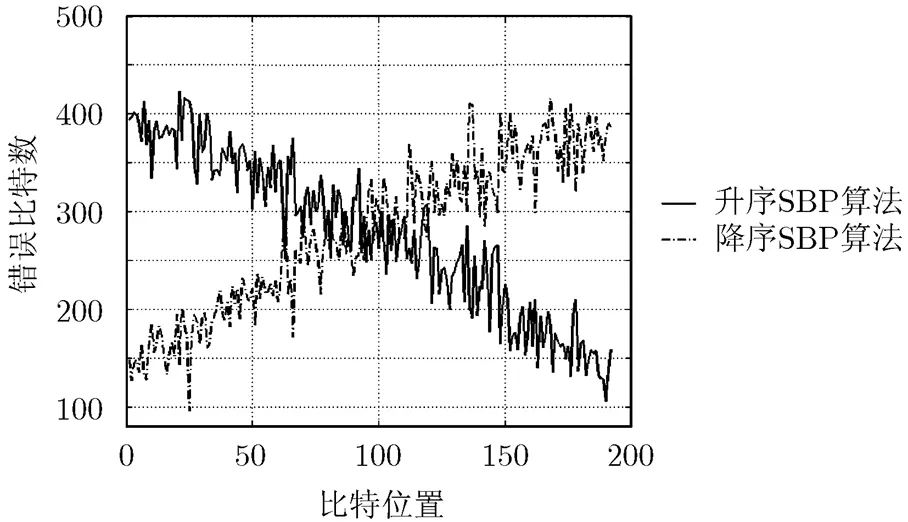
图1 采用不同更新顺序的SBP算法下各比特位置的错误比特数

3.1 OSBP算法

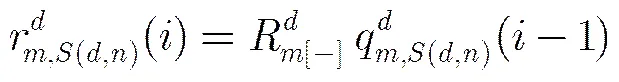
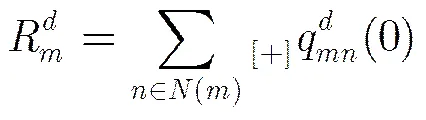
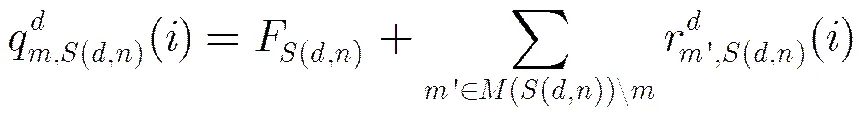
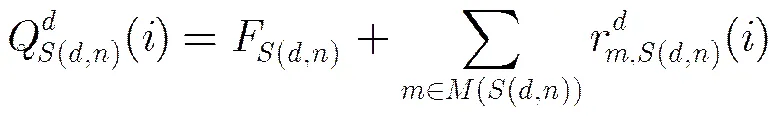
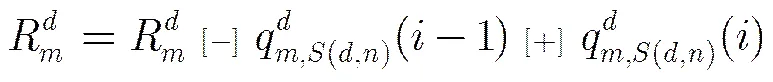
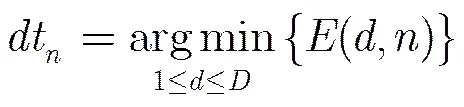
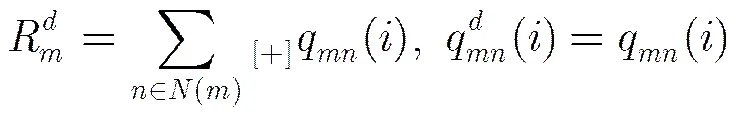
从第2步可以看出，不同于SBP算法，OSBP算法在每次迭代后只保留了最可靠的变量节点信息参与下一次迭代，所以得到了更好的性能。另外在每次迭代后，只需存储最可靠的信息，而可以方便地由得出，并不需要存储每个子译码器的变量节点信息，因此相比于SBP算法而言，并不需要额外的存储空间。

每个子译码器以不同的更新顺序同时进行迭代，每个变量节点都被各子译码器在不同的时间进行更新。正如3.2节里图2将要展示的那样，各子译码器的更新交叠在一起，相互之间传递更可靠的信息，故这里将该算法称之为交叠的Shuffled-BP算法。

与SBP算法一样，在实际工程实现中OSBP算法也可以方便地进行并行处理：设并行度为，变量节点平均分成组，每组个节点，对于每个子译码器而言，每组各节点并行更新，而不同组之间串行更新，此时在第1步中，当时，对于每个子译码器，每个，以及，式(14)应变为

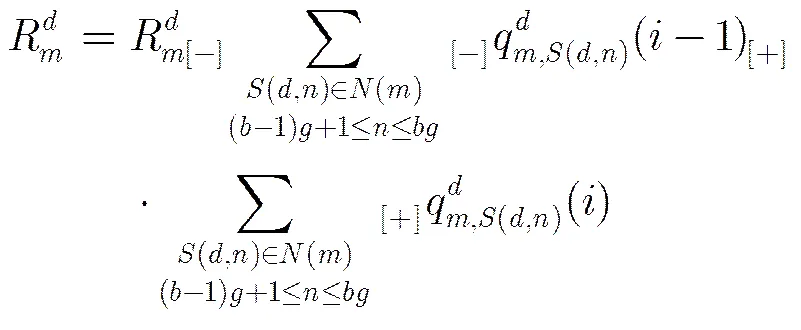
3.2最大化译码性能的更新顺序选取

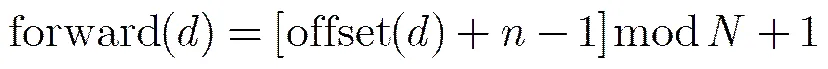
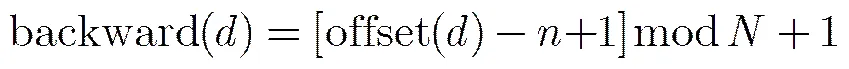
根据第2节的分析可知，越晚被更新的节点对应的错误率越低，所以不失一般性，这里将前向与后向更新顺序的错误率表示为如式(20)，式(21)的一种线性关系：

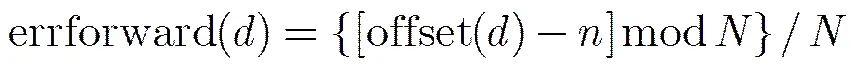
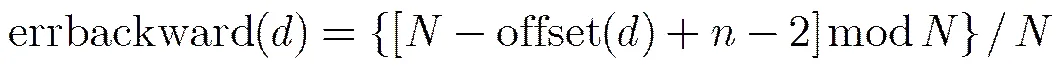
由此可见，各个子译码器的更新顺序直接影响OSBP算法的性能，为了最大化译码性能，将平均分成份，，并沿着变量节点等间隔地布置子译码器，每个等间隔点前后分别布置两个子译码器，子译码器的个数。在等间隔点处，，两个子译码器的偏移量分别为和，对应的更新方向分别为前向和后向更新，然后利用式(18)~式(21)就可以得出各子译码器的更新顺序和错误率。

图2表示了一次迭代中SBP算法与OSBP各子译码器更新过程的示意图：纵轴表示错误率，横轴表示节点位置。斜线上的箭头指示更新的方向，按箭头所指的方向进行更新，各斜线所对应横坐标的位置即为各子译码器更新的顺序。图中设子译码器的个数，在OSBP算法在每次迭代过程中，当时，各子译码器开始存储当前的信息，即对应于图2(b)中的阴影部分；而SBP算法在每次迭代中存储的信息对应于图2(a)中的阴影部分，可见OSBP算法在每次迭代后错误率更低。

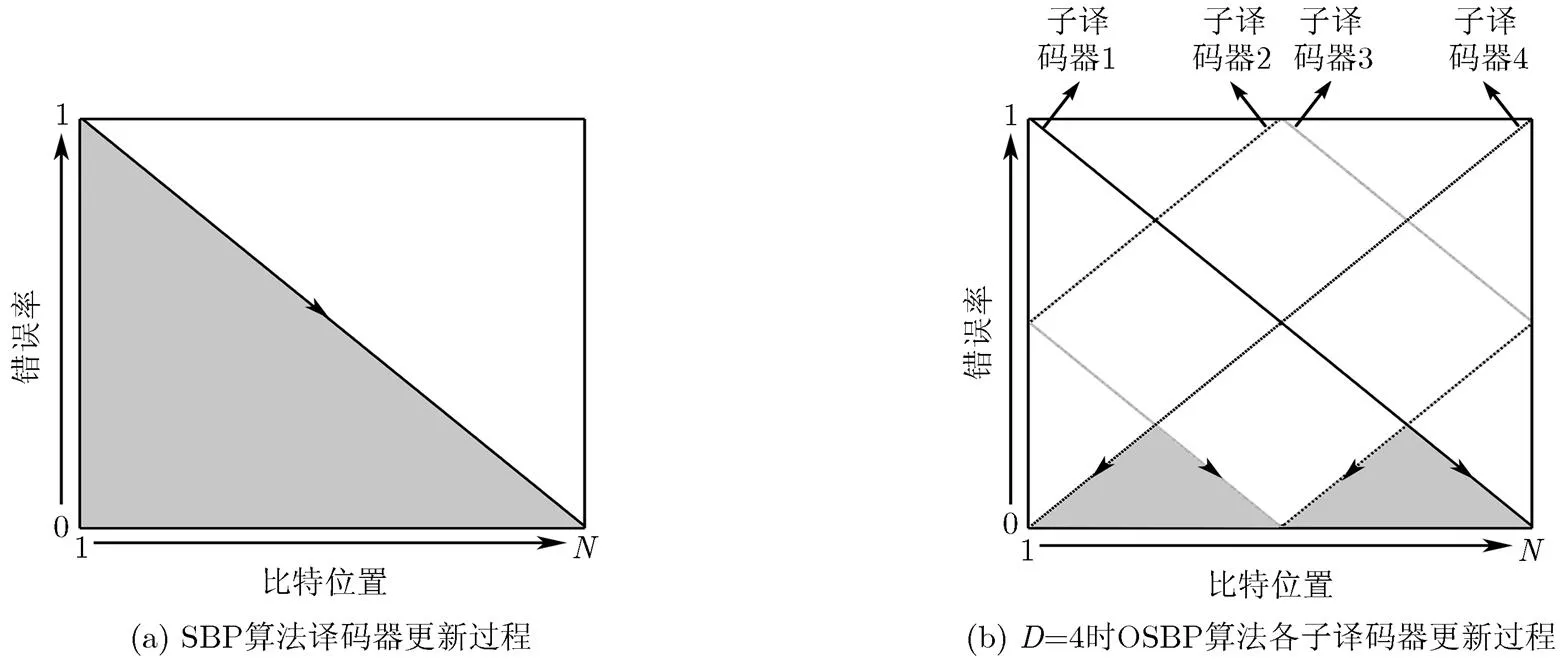
图2 SBP算法与OSBP各子译码器更新过程对比示意图

4 基于密度进化的收敛性分析

本节将采用高斯近似的密度进化理论，针对SBP和OSBP译码算法推导了其对应的消息均值进化，并基于该理论定量地分析了SBP算法和OSBP算法的收敛性。

密度进化(DE)是分析基于消息传递的迭代译码算法性能有效的理论工具，如果信道和译码算法均满足对称性条件，那么误码率与所传输的码字无关，这样可以假设传输码字均为0，以大大减化DE算法的复杂度。然而即便如此，由于需要精确计算节点消息的概率密度，DE算法的计算量仍然非常巨大，文献[14]提出了高斯近似的方法，将多维节点消息的DE简化为1维均值的进化，大大降低了DE的计算量，并且由其计算出来的译码门限与精确的DE所得到的结果仅仅相差0.3%~1.2%，保证了分析的有效性。

不同于BP译码算法，在SBP算法下，节点的概率密度与比特位置有关。令和分别为第次迭代中对应于第个比特位置的变量消息密度和校验消息密度的均值，则对于规则LDPC码来说(其中与分别为变量节点与校验节点的度数)，第次迭代时变量消息的均值进化与BP译码算法下的一致，表示为

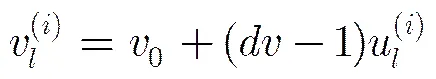
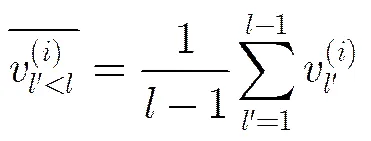
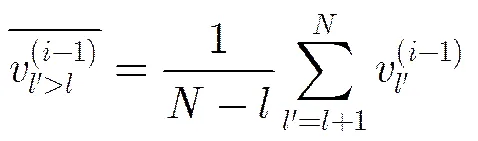
参与校验消息均值进化的变量消息均值的所有可能的组合数为

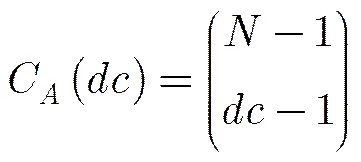
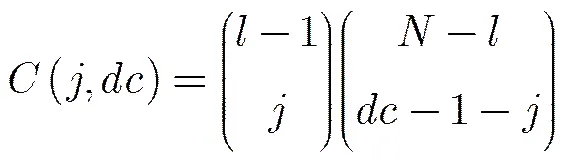
那么在SBP译码算法下，校验消息均值的进化可以表示为

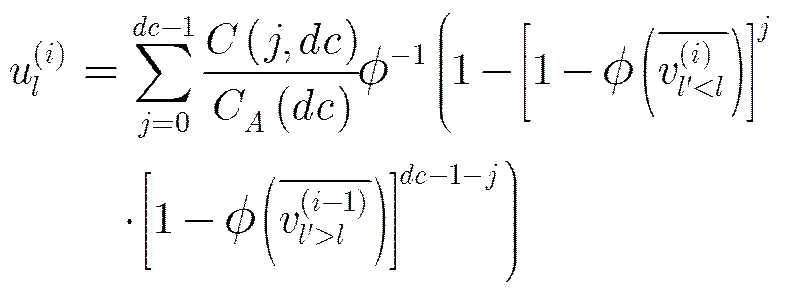
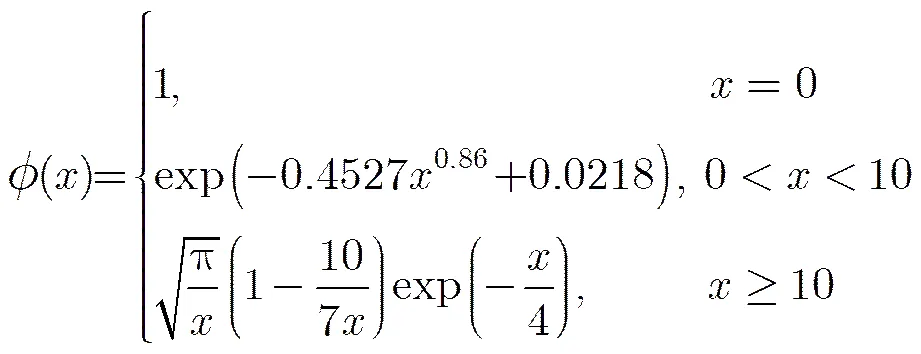
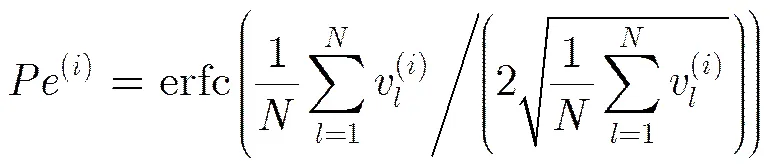
由SBP译码算法下的消息均值进化规则可以方便地得到OSBP算法的消息均值进化规则。由式(10)~式(16)可以看出，OSBP算法中变量消息均值的进化与SBP算法的一致，如式(22)所示，不同之处在于校验消息均值的进化。由于在OSBP算法中，每次迭代时只保留了对应每个比特位置最可靠子译码器的输出外信息，所以变量消息的均值进化需要加入如式(30)过程：

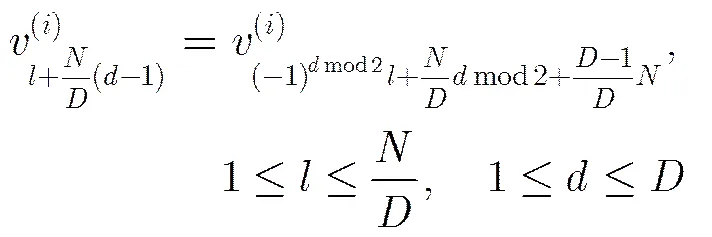
到SBP算法与OSBP算法下的消息均值进化。在SBP算法下，第次迭代过程中度数为的变量消息均值进化可以表示为

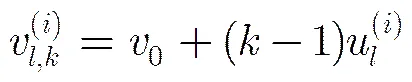
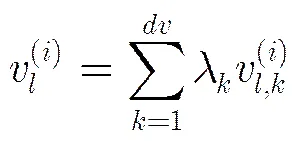
令

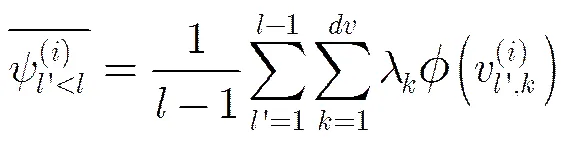
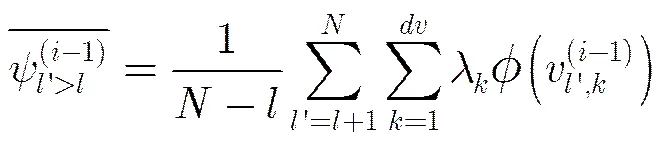
那么校验消息的均值进化可以表示为

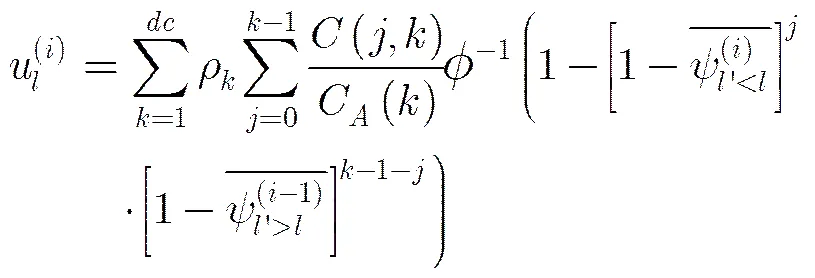
图3描绘了通过密度进化分析所得到的SBP算法和OSBP算法在不同迭代次数下的误比特率。图3(a)采用码率为1/2的(3,6)规则LDPC码，信噪比为1.2 dB；图3(b)采用码率为1/2的非规则LDPC码，最大变量节点度数为5，其度分布与文献[15]中的一致，信噪比为0.9 dB。由图3可知，无论对于规则还是非规则LDPC码，OSBP算法的收敛速度均快于SBP算法，并且子译码器个数越大，OSBP算法的收敛速度越快；在相同的迭代次数下，OSBP算法的误比特率低于SBP算法，并且误比特率随的增大而减小。

密度进化分析的前提是码长无限长、校验矩阵中的‘1’随机分布，故其得到的具体的迭代次数对于实际有限长的LDPC码来说是一个相对值，并不能反映实际所需的迭代次数。为了得到子译码器个数与译码延时的关系，这里将OSBP算法的迭代次数相对于SBP算法下的迭代次数进行归一化：令表示子译码器个数为时OSBP算法所需要的迭代次数，表示SBP算法所需要的迭代次数，则OSBP算法的译码延时为

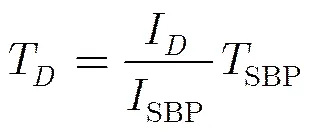
5 仿真结果及分析

为了验证本文所提出OSBP算法的性能，本文以两种码率为1/2的LDPC码为例：(1)文献[16]中准循环构造算法构造的环长为8、码长为192的(3,6)规则LDPC码，这里称之为C1码；(2)文献[15]中变量节点度分布为，并采用文献[17]中改进的PEG算法构造的码长为1024的非规则LDPC码，这里称之为C2码。在AWGN和BPSK调制的条件下，采用蒙特卡洛仿方法，对OSBP算法与SBP算法的性能做了对比仿真实验。

图4分别表示了C1码和C2码在采用OSBP算法和SBP算法下的误比特率。其中C1码的信噪比为3.0 dB; C2码的信噪比为2.0 dB; OSBP算法的子译码器个数分别取2, 4, 8。由图4可知，在相同的迭代次数和信噪比的条件下，本文算法的误比特率相比于SBP算法降低了一半以上，并且当增加时，误比特率会进一步有小幅度的降低，且越大，降低的幅度越小。

图5分别表示了C1码和C2码在采用两种译码算法下的误码曲线。其中OSBP算法的子译码器个数为4。由图5可以看出在相同的最大迭代次数下，相比于SBP算法，本文提出的OSBP算法有着更优的误码性能，最大迭代次数越少，这种优势越明显。对于C1码而言，在误比特率等于的条件下，误码性能提升了大约0.3 dB。对于C1码和C2码来说，当最大迭代次数分别大于5次和10次的条件下，本文提出的OSBP算法仍然保持有略微的优势。

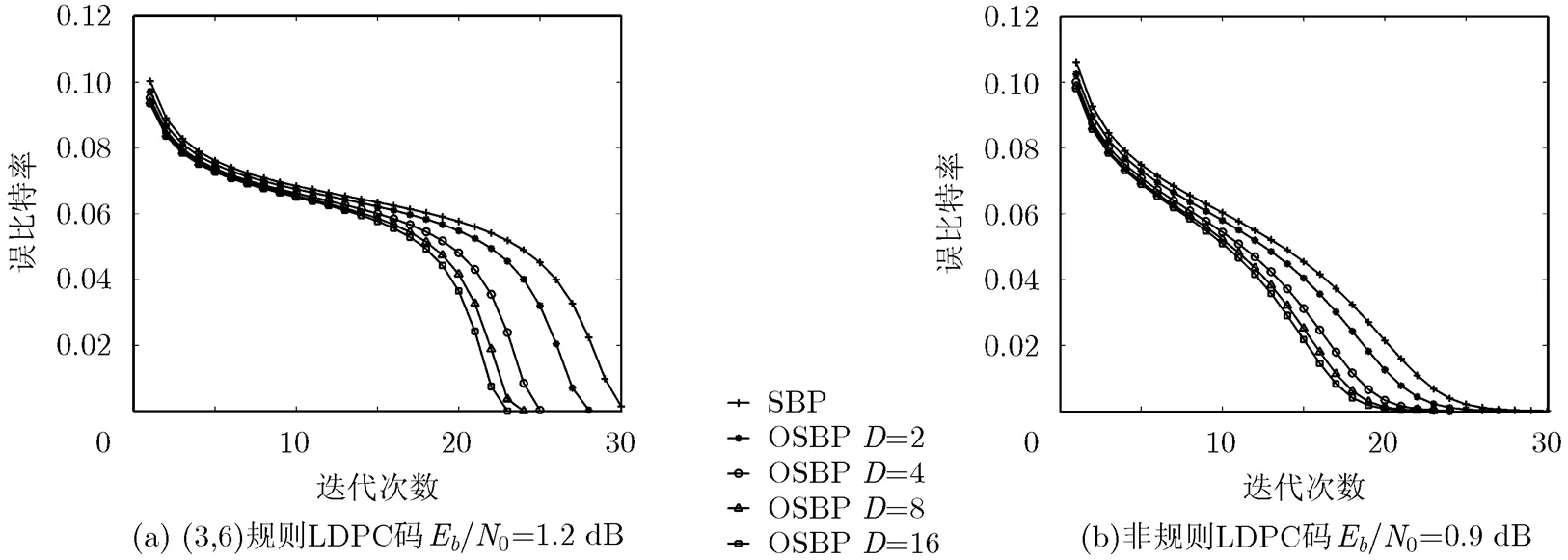
图3通过密度进化分析得到的不同迭代次数下的误比特率

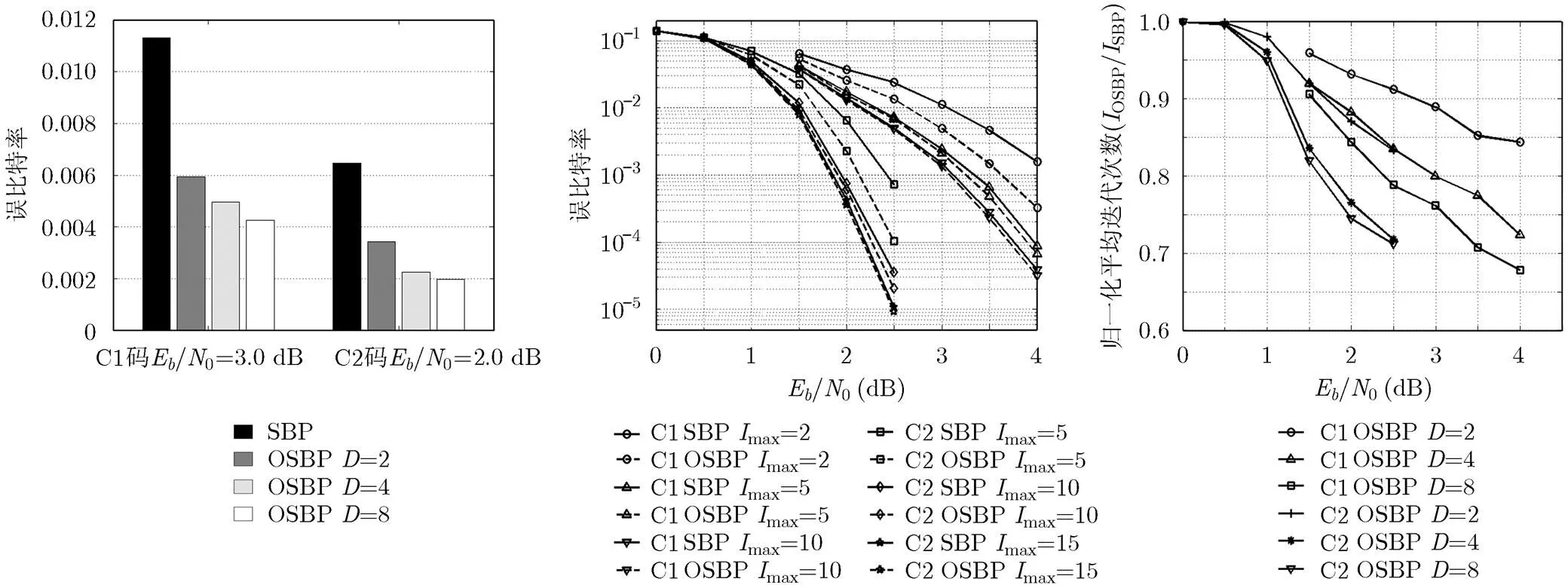
图4 OSBP算法与SBP算法     图5 OSBP算法与SBP     图6 OSBP算法与SBP算

在特定信噪比下的误比特率     算法误码性能的比较仿真     法平均迭代次数的比较仿真

6 结束语

本文为了进一步提升Shuffled-BP(SBP)算法的性能提出了一种交叠的Shuffled-BP(OSBP)迭代译码算法，通过充分利用SBP算法中变量节点信息的可靠性随更新时间增加而提升的特点，采用若干个相同的子译码器同时交叠地对LDPC码进行更新迭代，相互之间生成并传递更可靠的信息，从而进一步提高SBP算法的收敛速度和误码性能。基于密度进化理论对提出的算法进行了分析，证明了OSBP算法的误码性能和收敛速度均优于SBP算法。仿真实验表明，本文的算法对于规则LDPC码和非规则LDPC码均有效，在不增加额外存储空间的条件下，OSBP算法的误码性能优于SBP，并且其误比特率随着子译码器个数的增加而降低，尤其在中高信噪比区间下，误码性能较SBP算法提升约1倍。除此之外，相比于SBP算法，OSBP算法有着更快的收敛速度，并且其收敛速度随着码长和子译码器个数的增加而增加，所以在实际工程应用中，OSBP算法可以带来更大的编码增益和更低的译码延时。

[1] SHANNON C E. A mathematical theory of communi- cation[J]., 2001, 5(1): 3-55.

[2] MACKAY D J C and NEAL R M. Near Shannon limit performance of low density parity check codes[J]., 1996, 32(18): 1645-1646.

[3] GALLAGER R G. Low-density parity-check codes[J]., 1962, 8(1): 21-28.

[4] HOCEVAR, D. A reduced complexity decoder architecture via layered decoding of LDPC codes[C]. IEEE Workshop on Signal Processing Systems (SIPS), Austin, TX, USA, 2004: 107-112.

[5] ZHANG Xinmiao and TAI Ying. High-speed multi-block-row layered decoding for Quasi-cyclic LDPC codes[C]. IEEE Global Conference on Signal and Information Processing (GlobalSIP), Atlanta, GA, USA, 2014: 11-14.

[6] ZHANG J and FOSSORIER M. Shuffled belief propagation decoding[C]. Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 2002, 1: 8-15.

[7] WU Sheng, JIANG Xiaobo, and NIE Zhenghua. Alternate iteration of shuffled belief propagation decoding[C]. International Conference on Communications and Mobile Computing (CMC), Shenzhen, China, 2010, 2: 278-281.

[8] LAOUINI N, BEN Hadj Slama L, and BOUALLEGUE A. An optimized min-sum variable node layering for LDPC decoding[C]. International Conference on Multimedia Computing and Systems (ICMCS), Marrakech, Morocco, 2014: 794-799.

[9] SUN Yang and CAVALLARO J R. VLSI architecture for layered decoding of QC-LDPC codes with high circulant weight[J].(), 2013, 21(10): 1960-1964.

[10] ASLAM C A, GUAN Yongliang, and CAI Kui. Improving the belief-propagation convergence of irregular LDPC codes using column-weight based scheduling[J]., 2015, 19(8): 1283-1286.

[11] LIU Xingcheng, ZHANG Yuanbin, and RU Cui. Variable-node-based dynamic scheduling strategy for belief-propagation decoding of LDPC codes[J]., 2015, 19(2): 147-150.

[12] LI Jia, YANG Gaigai, and ZHAO Zhiqiang. An improved-performance decoding algorithm of LDPC codes for layered decoding[C]. IEEE International Conference on Communication Problem-Solving (ICCP), Beijing, China, 2014: 318-321.

[13] HAGENAUER J, OFFER E, and PAPKE L. Iterative decoding of binary block and convolutional codes[J]., 1996, 42(2): 429-445.

[14] CHUNG Saeyoung, RICHARDSON T J, and URBANKE R L. Analysis of sum-product decoding of low-density parity-check codes using a Gaussian approximation[J]., 2001, 47(2): 657-670.

[15] RICHARDSON T J, SHOKROLLAHI M A, and URBANKE R L. Design of capacity-approaching irregular low-density parity-check codes[J]., 2001, 47(2): 619-637.

[16] ZHANG Yi and DA Xinyu. Construction of girth-eight QC-LDPC codes from arithmetic progression sequence with large column weight[J]., 2015, 51(16): 1257-1259.

[17] JIANG Xueqin, XIA Xianggen, and LEE Moonho. Efficient progressive edge-growth algorithm based on Chinese remainder rheorem[J]., 2014, 62(2): 442-451.

An Overlapped Shuffled-BP LDPC Decoding Algorithm

FAN Yanan①②WANG Lichong①②YAO Xiujuan①MENG Xin①

①(,,100190,)②(,100190,)

Shuffled-BP (SBP) decoding algorithm is a variable-node-based serial decoding algorithm, which converges faster than the original Belief-Propagation (BP) decoding algorithm. However, due to the semi-parallel processing, there is a decrease in terms of convergence speed and error performance. An Overlapped Shuffled-BP(OSBP) decoding algorithm is proposed to enhance further the performance of the Shuffled-BP algorithm. In this algorithm, more than one sub-decoders are used to execute simultaneously, every sub-decoder has different updating order from each other. Regarding each variable node, the most reliable messages are kept and used for the next iteration, thus a faster convergence can be provided. Both theoretical analysis and simulation results show that, compared with SBP algorithm, OSBP algorithm possesses a better error performance as well as a higher convergence speed and introduces no extra storage requirement. Moreover, the proposed algorithm is effective for both regular and irregular LDPC codes.

Low Density Parity Check (LDPC) code; Convergence speed; Decoding algorithm; Shuffled-BP; Overlapped Shuffled-BP

TN911.22

A

1009-5896(2016)11-2908-08

10.11999/JEIT151477

2015-12-29；改回日期：2016-06-03；

2016-07-19

范亚楠 fanyanan_99@163.com

中国科学院创新基金(CXJJ14S126)

CAS Innovation Foundation (CXJJ14S126)

范亚楠： 男，1991年生，博士生，研究方向为星间通信系统中的信道编译码技术.

王丽冲： 女，1990年生，硕士生，研究方向为分布式卫星组网建模与仿真.

姚秀娟： 女，1977年生，研究员，研究方向为卫星组网通信与模式识别技术.