基于半正定松弛的MIMO盲检测

李 浩 彭 华



基于半正定松弛的MIMO盲检测

李 浩*彭 华

(解放军信息工程大学信息系统工程学院 郑州 450001)

为解决MIMO系统盲检测问题，该文以最大似然序列检测为估计准则，通过推导建立了一种新的半正定松弛(SemiDefinite Relaxation, SDR)求解模型，使得到的松弛解的秩等于发送天线数。为了解决了松弛解秩大于1时估计原始发送序列的难题，该文提出一种特征向量近似法和随机法相结合的方法。通过限定目标函数的取值上限，使算法能够根据目标函数值自适应判断求解发送序列个数，从而减少每次求解的约束个数和SDR的求解次数，分析表明算法的计算复杂度与发送天线数成线性关系。最后，通过仿真表明所提算法能够在与秩1的算法性能保持相当的条件下减少计算时间，并验证了算法计算复杂度与发送天线数成线性关系。

多输入多输出；盲检测；半正定松弛

1 引言

近年来，半正定松弛由于其低计算复杂的特点被广泛应用于信号处理和通信领域[1,2]，对于一些十分困难的优化问题，半正定松弛是一种十分有效的次最优算法，通常在计算复杂度和性能上具有较好的折中。BPSK信号的MIMO检测可以看作布尔二次规划(Boolean Quadratic Program, BQP)问题，对其做适当的替换和松弛就能够变为半正定规划(semidefinite program)，从而将NP-Hard问题转变为凸优化问题，该问题可以用内点法(interior point method)进行求解，而计算复杂度仅为多项式级，这种对原问题进行松弛、通过对半正定规划求解的方法被称为半正定松弛。

半正定松弛(SemiDefinite Relaxation, SDR)应用于MIMO非盲检测的文献出现在本世纪初[3]。紧接着，文献[4,5]对利用SDR实现MIMO软检测进行了讨论。之后，文献[6,7]分别利用SDR实现了对M-PSK信号和高阶QAM信号的MIMO检测，文献[8]对高阶信号检测的各种方法的性能与复杂度进行了分析与比较。与此同时，许多学者与对基于SDR的MIMO检测算法做了性能分析，其中文献[9,10]对SDR检测与最大似然(Maximum Likelihood, ML)检测的等价准则进行了讨论，给出了SDR算法与ML的等价条件。另外一些研究人员[11,12]则对算法在不同信噪比等条件下的检测性能进行了讨论，证明了许多重要的结论与定理，并对误码性能的理论限做了分析，进一步完善了基于SDR的MIMO检测算法的理论体系。

针对MIMO盲检测问题，文献[13]利用OSTBC的正交性实现了基于SDR的OSTBC盲最大似然检测，但对于BLAST (Bell Labs Layered Space Time)方案则无法应用。文献[14]通过加入信源相关性的约束条件用SDR实现了已知符号集的盲源分离，该算法可以应用于MIMO信号的盲检测，但算法建立的SDR模型的秩仅为1，对每一个信源都要进行一次求解，因此计算复杂度较高，为叙述方便我们称这种算法为秩1的盲检测算法。

本文致力于MIMO系统的盲检测问题，安排如下：第1节为前言；第2节介绍MIMO盲检测的信号模型和估计准则；第3节将MIMO盲检测问题转换为二次约束的二次规划(Quadratically Constrained Quadratic Program, QCQP)问题，并做适当的松弛建立一种新的MIMO盲检测SDR求解模型；第4节提出一种主特征向量和随机法相结合的方法估计原始问题的解，解决了松弛解秩大于1条件下估计原始问题解的难题；第5节通过分析SDR模型目标函数的误差上限来设定检测序列个数门限，加入信源相关性的约束条件，设计了松弛解的个数能够自适应变化的SDR MIMO盲检测算法，并对算法的计算复杂度了进行分析；第6节给出算法的仿真结果与对比；最后对全文算法进行总结。

2 信号模型

考虑MIMO系统接收端的接收信号模型，假设信号精确同步(包括载波同步和定时同步等)，系统中有个接收天线和个发送天线，每个天线发送个符号，且不失一般性假设各信源独立，定义：

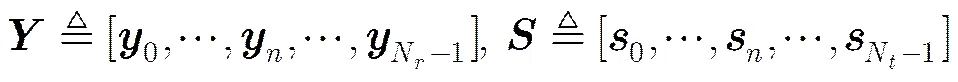
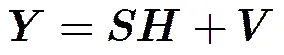
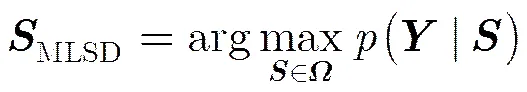
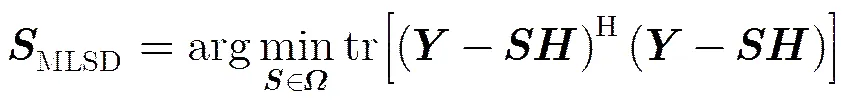
3 半正定松弛(SDR)求解模型

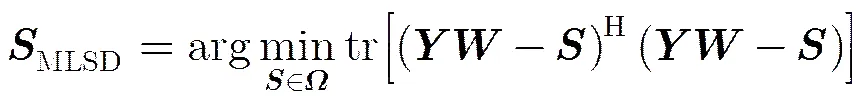
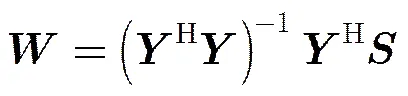
将式(6)代入式(5)可得发送信号的最大似然序列估计式等价为

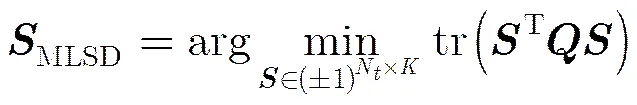
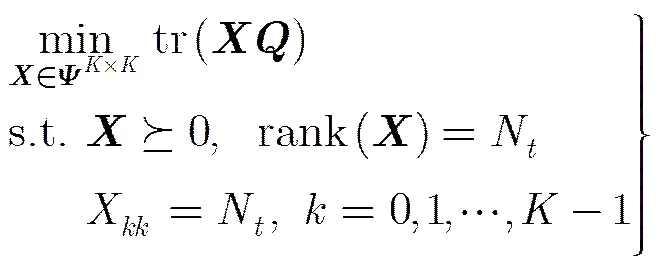
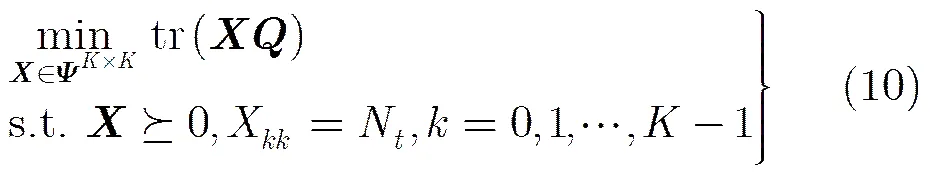
该问题是一个凸优化问题，文献[1,8]给出了用内点法、CVX工具箱等求解算法和工具，由此可以得到松弛解。上面论述虽然以BPSK信号为例进行说明，但是QPSK, 16QAM等复信号和多模的PAM信号也能够通过变量代换、实虚分解等变换得到QCQP模型并通过松弛得到式(10)，只是模型维数有所增加，具体方法可以参考文献[16]等。

4 原始问题求解

4.1 特征向量近似

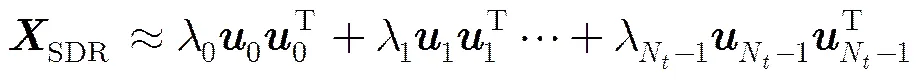
4.2随机法

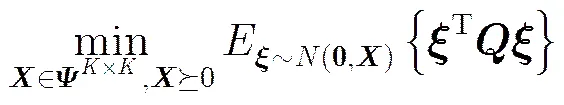
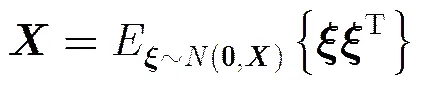
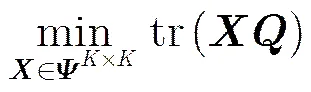
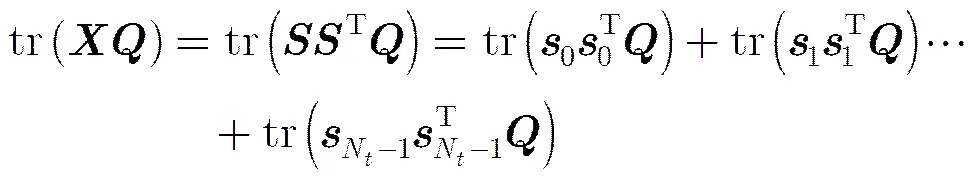
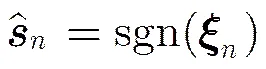
另外，信源之间虽然独立，但是因为数据长度有限，任意两个发送序列通常具有相关性，所以需要通过相关系数的大小判定两个序列是否“独立”。序列的期望为0，方差为1，根据相关系数的公式可得

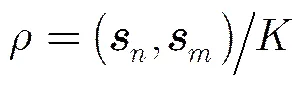
5 算法分析与总结

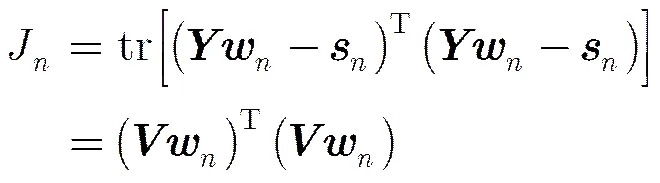
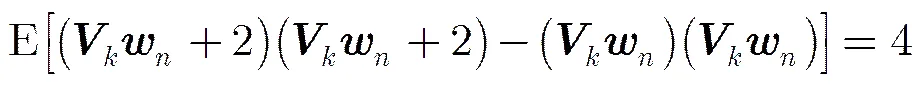
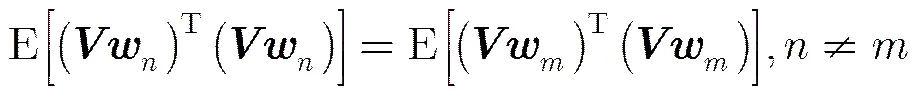
由此可以得出以下两个结论：(1)最小的目标函数值对应的发送序列的估计值最准确误码率最低；(2)如果其他发送序列估计值与最小的目标函数值对应的发送序列估计值具有相近的误码率，则两者的目标函数值相差不大。因此，可以通过其他目标函数值与最小的目标函数值的差值来判断该发送序列估计值的误码率能否与最优的估值序列相近。令

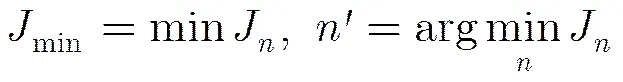
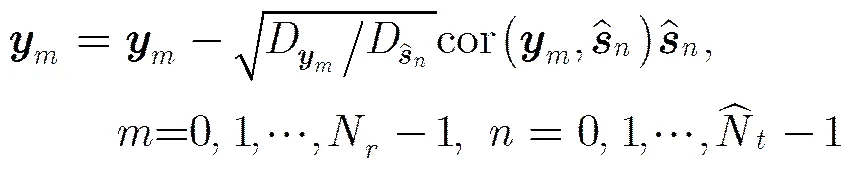
步骤2 加入表示发送序列“独立”的约束条件，令待求解序列的相关性与已求解序列的相关性小于相关阈值，即，其中，由此得到新的SDR模型：

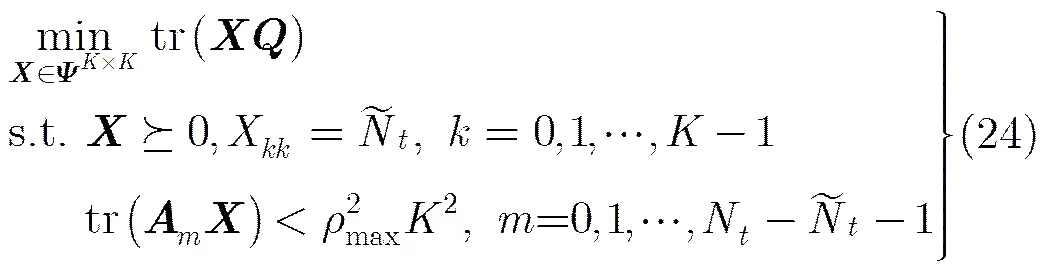
下面对算法的计算复杂度进行分析，每次SDR求解算法内点法在给定计算精度的条件下计算复杂度为，一般为常数，因而记为，其中表示约束条件个数，式(24)中对角线元素的约束互不相关，因而可看作1个约束条件。上述算法中特征值分解的计算复杂度是，秩1的算法和上述算法所应用的Cholesky分解的计算复杂度是，两种算法中每次SDR求解的随机的计算复杂度均是，由此可以看出两种算法的计算消耗主要集中在内点法求解。秩1算法做了次SDR求解，每次求解的约束条件个数都增加1个，可得次SDR求解的计算复杂度为

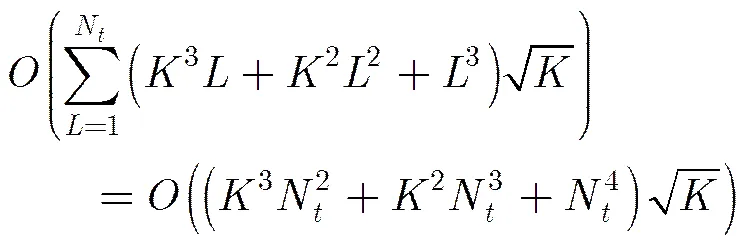
6 仿真实验

为了对比本文提出的算法(Rank-adaptive)和秩1的算法(Rank-1)的性能给出以下仿真实验，每组实验进行500次蒙特卡洛仿真，实验条件如下：(1)发送序列：发送序列为相互独立的随机序列，若无特殊说明则信号长度为100(即)，发送信号是调制方式为BPSK的信号；(2)发送接收天线数：若无特殊说明接收天线数与发送天线数相等，一般选取；(3)随机信道：试验采用随机信道，则每次蒙特卡洛仿真中MIMO信道矩阵的系数随机产生，各元素(若信道为复信道则实部和虚部独立)均服从均值为0、方差为1的高斯分布；(4)信噪比：定义信噪比为

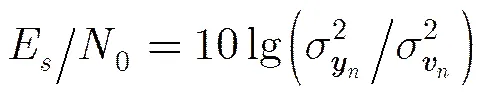
第1组实验对比本文提出的算法和秩1的算法在不同信噪比条件下的性能，实验进行了500次蒙特卡洛仿真，每次仿真的发送序列和信道系数均按上述方法产生。图1给出了该组实验的仿真结果，图中纵轴表示误比特率，横轴表示信噪比，4条曲线分别表示秩1的算法、本文提出的算法在,和时的性能曲线。由结果可以看出在相同的发送接收环境下，本文提出的算法在时与秩1算法的误比特性能几乎相同，算法性能随的增长而下降。由第5节的分析可知，两种算法的计算消耗主要集中在内点法求解过程，因此本文以SDR求解的次数和求解时间作为对比标准。表1给出了4种算法在不同信噪比下SDR平均求解次数，从仿真结果可以看出本文算法在时的SDR求解次数减少50% 以上，且随的增长而下降，当时则只需1次SDR求解。表2 给出了4种算法在不同信噪比下CVX工具箱求解SDR的平均时间，从求解时间来看计算复杂度降低了56%以上，比SDR求解次数降低的比例更高。这是因为SDR求解的计算复杂度随约束条件个数成多项式级增加，而求解次数与约束条件有线性关系，所以求解时间会随求解次数成多项式级增加，表1和表2中的数据恰好反映了这一关系。

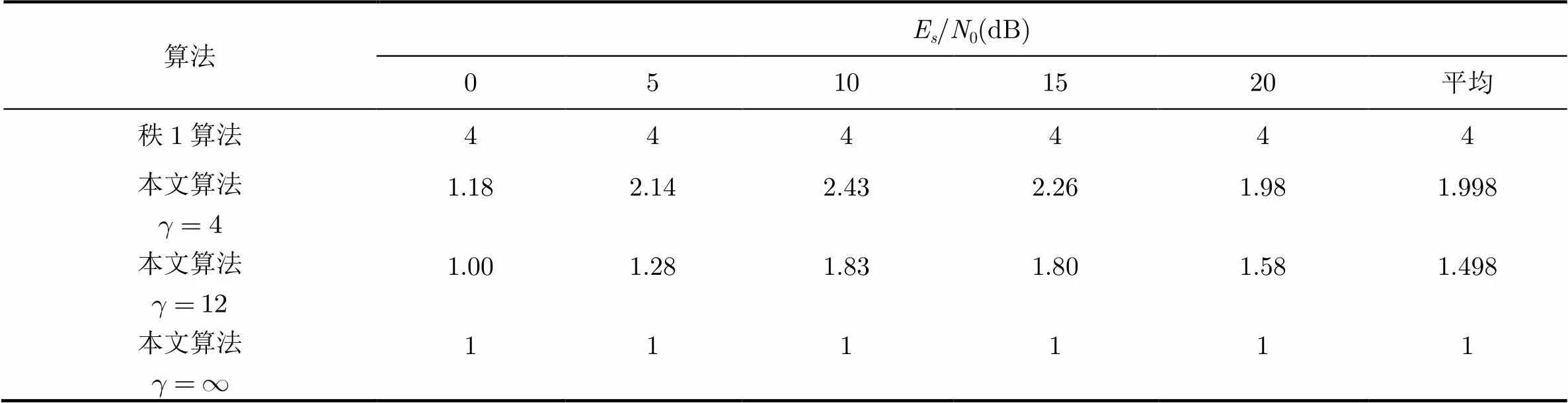
表1 4 种算法在不同信噪比下SDR平均求解次数

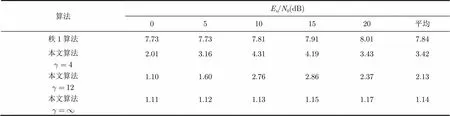
表2 4种算法在不同信噪比下平均求解时间(s)

由于发送天线数的增加会增加松弛解秩的维度，因此第2组实验将对比不同发送天线数对算法的影响。图2给出了该组实验的仿真结果，图中纵轴表示误比特率，横轴表示信噪比，其中两条实线分别表示发送天线数为6时秩1算法和本文算法()的性能曲线，虚线则表示发送天线数为8时秩1算法和本文算法()的性能曲线，可以看出两种算法的性能曲线几乎相同，表明发送天线数对本文算法与秩1算法的影响相同。由于平均求解时间更能反映计算复杂度，因此给出了不同发送天线数在不同信噪比下平均求解时间，如表3所示。可以看出本文算法的平均求解时间在时为5.16 s，在时仅为6.95 s，与秩1算法相比，分别减少66%和72%。为更加直观地给出算法复杂度的对比，在综合表2，表3的数据的基础上对,时进行算法仿真，记录两种算法的平均求解时间，图3给出了仿真结果。图中横轴表示发送天线数，纵轴表示平均求解时间，可以看出秩1算法的平均求解时间随发送天线数的增加近似成多项式级上升，而本文算法的平均求解时间与发送天线数则成线性关系，仿真结果验证了第5节中对算法计算复杂度的分析。

表3算法在不同发送天线数下平均求解时间(s)

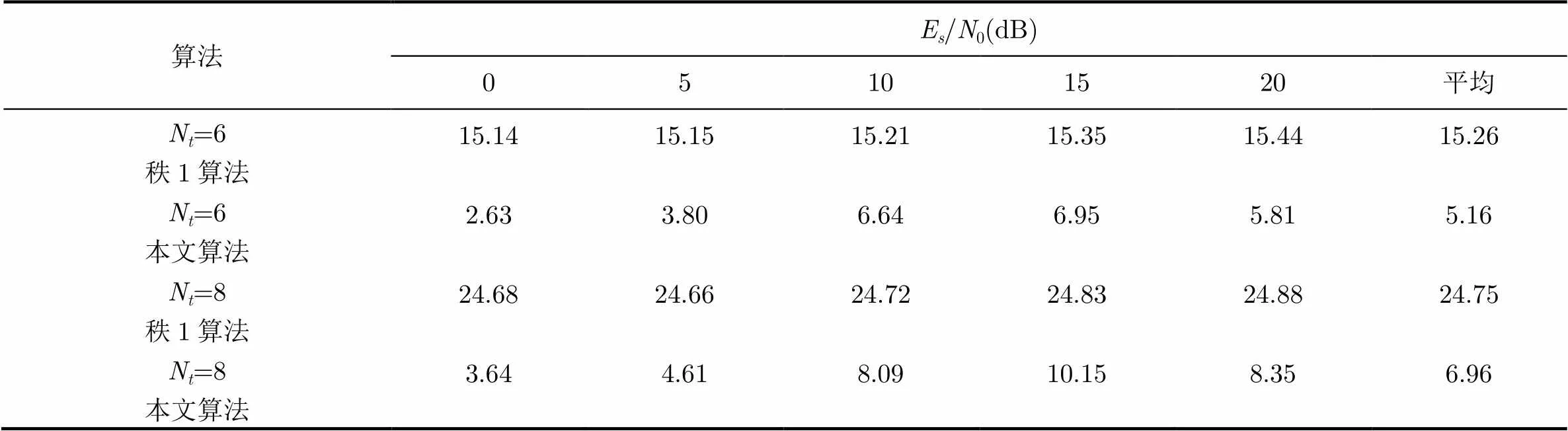
算法Es/N0(dB) 05101520平均 Nt=6秩1算法15.1415.1515.2115.3515.4415.26 Nt=6本文算法2.633.806.646.955.815.16 Nt=8秩1算法24.6824.6624.7224.8324.8824.75 Nt=8本文算法3.644.618.0910.158.356.96

第3组实验对比一定信噪比条件下不同发送序列长度的对算法的影响，图4给出了信噪比为15 dB时该组实验的仿真结果，图中纵轴表示误比特率，横轴表示发送序列的长度，两条曲线分别表示秩1的算法、本文提出的算法在时的性能曲线。仿真结果可以看出算法性能随数据量的增加而提升，该实验结果验证了信源“独立”对于算法的影响，数据长度越长信源的独立性越明显，盲检测的效果越好。

第4组实验对比不同接收天线数对算法的影响，图5给出了该组实验的仿真结果，图中纵轴表示误比特率，横轴表示信噪比，其中两条实线分别表示接收天线数为5时秩1算法和本文算法的性能曲线，虚线则表示接收天线数为3时秩1算法和本文算法的性能曲线。仿真结果表明当接收天线数增多时，由于接收到更多的信号副本使得两种算法的性能均得到提升，且两种算法的性能在超定的情况下几乎相同，但在欠定的情况下两种算法均有较大的性能损失，并且本文算法的性能损失更为明显，这是因为本文算法松弛解的秩与发送天线数相同，当接收天线数小于发送天线数时由于接收维度的缺失，会使松弛解的秩等于接收天线数，进而导致原始问题解的估计误差增大、误码率增加。

7 总结

本文致力于MIMO系统的盲检测问题，以最大似然序列检测为准则，建立了一种新的SDR求解模型，使得松弛解的秩等于发送天线数，并根据松弛解的秩大于1的特点还提出了一种特征向量和随机法相结合的估计原始问题解的方法，通过限定目标函数的取值上限，使算法自适应对多路发送序列进行检测，且算法的计算法复杂度与发送天线数成线性关系。最后，通过仿真验证了本文算法能够在与秩1的算法性能保持相当的条件下降低计算复杂度，计算复杂度的改善随发送天线数的增加而更加明显。

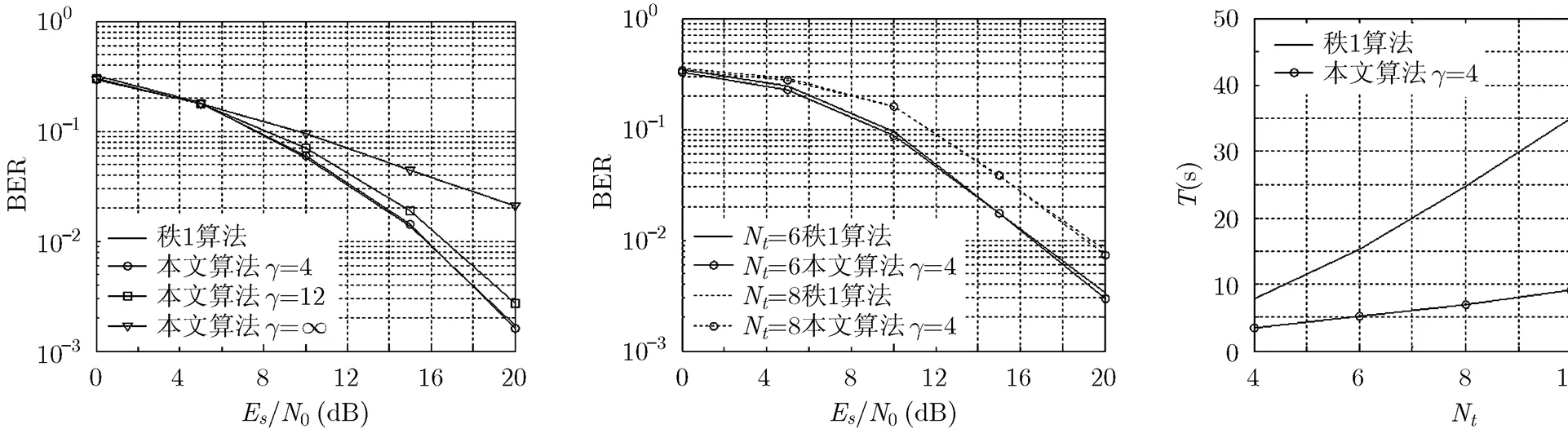
图1 不同信噪比下算法性能对比 图2 不同发送天线数算法性能对比 图3 不同发送天线数下平均求解时间

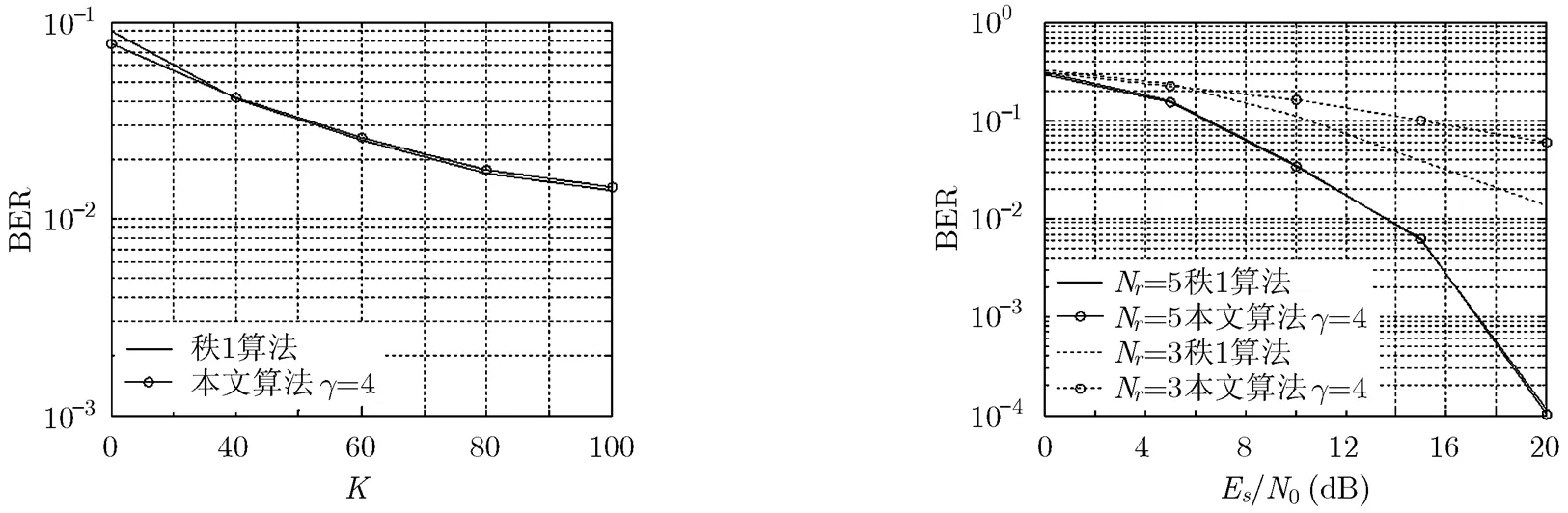
图4 不同数据量算法性能对比 图5 不同接收天线数算法性能对比

[1] LUO Zhiquan, MA Wingkin, ANTHONY S M,. Semidefinite relaxation of quadratic optimization problems[J]., 2010, 27(3): 20-34.

[2] 罗涛, 刘宏伟, 严俊坤, 等. 基于半正定秩松弛方法的稳健波束形成[J]. 电子与信息学报, 2014, 36(7): 1545-1551. doi: 10.3724/SP.J.1146.2013.01046.

LUO Tao, LIU Hongwei, YAN Junkun,. Robust beamforming via semidefinite rank relaxation[J].&, 2014, 36(7): 1545-1551. doi: 10.3724/SP.J.1146.2013.01046.

[3] MA Wingkin, DAVIDSON T N, WONG K M,. Quasi- maximum-likelihood multiuser detection using semi-definite relaxation with application to synchronous CDMA[J]., 2002, 50(4): 912-922.

[4] STEINGIMSSON B, LUO Zhiquan, and WONG K. Soft quasi-maximum-likelihood detection for multiple-antenna wireless channels[J]., 2003, 51(11): 2710-2719.

[5] NEKUII M, KISIALIOU M, DAVIDSON T N,. Efficient soft-output demodulation of MIMO QPSK via semidefinite relaxation[J]., 2011, 5(8):1426-1437.

[6] MA Wingkin, CHING Pakchung, and DING Zhi. Semidefinite relaxation based multiuser detection for M-ary PSK multiuser systems[J]., 2004, 52(10): 2862-2872.

[7] WIESEL A, ELDAR Y C, and SHAMAI S.Semidefinite relaxation for detection of 16-QAM signaling in MIMO channels[J]., 2005, 12(9):653-656.

[8] SHAO Z Y, CHEUNG S W, and YUK T I. Comparison of semidefinite relaxation detectors for high-order modulation MIMO systems[J]., 2014, 6(3): 1-8.

[9] JALDEN J, MARTIN C, and OTTERSTEN B. Semidefinite programming for detection in linear systems-optimality conditions and space-time decoding[C]. Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing, Hong Kong, 2003: 9-12.

[10] KIM Minjoon, PARK Jangyong, KIM Kilhwan,. Exact ML criterion based on semidefinite relaxation for MIMO systems[J]., 2014, 21(3): 343-346.

[11] JALDEN J and OTTERSTEN B.The diversity order of the semidefinite relaxation detector[J]., 2008, 54(4): 1406-1422.

[12] XU Zi, HONG Mingyi, and LUO Zhiquan. Probabilistic analysis of semidefinite relaxation for binary quadratic minimization[J]., 2014, 24(3): 1265-1293.

[13] 韩飞. 正交空时分组码的最大似然盲检测算法研究[D]. [硕士论文], 西南交通大学, 2014.

[14] LI Qingyu, BAI Erwei, and DING Zhi. Blind source separation of signals with known alphabets using epsi- approximation algorithms[J]., 2003, 51(1): 1-10.

[15] MANUEL A and MIGUEZ V J. Maximum-likelihood sequence detection in time- and frequency-selective MIMO channels with unknown order[J]., 2009, 58(1): 499-504.

[16] 薛江. 基于多通道接收的短波信道盲均衡算法研究[D]. [硕士论文], 解放军信息工程大学, 2012.

Blind Detection of MIMO via Semidefinite Relaxation

LI Hao PENG Hua

(,,450001,)

In order to solve the problem of blind detection of MIMO system, this paper takes maximum-likelihood sequence detection as the criterion and derives the formulas to get a model based on SemidDefinite Relaxation. The rank of SDRsolution equals to the number of the transmit antennas. For the rank of SDRsolution is greater than 1, a new method is proposed to approximate the solution of the original problem, which combines the eigenvector approximation method and randomization method. By setting the upper limit of objective function, the proposed method could judge the number of detection sequence adaptively and reduce constrains number and the number of solving SDR. The analysis shows that the computation complexity of proposed method has linear relationship with the number of transmit antennas. At last, simulation results indicate that compared with Rank-1 algorithm, the proposed detector could provide the same bit error performance with decrease of computation cost, and validate the linear relationship between the computation complexity and the number of transmit antennas.

Multiple-Input Multiple-Output (MIMO); Blind detection; SemiDefinite Relaxation (SDR)

TN92

A

1009-5896(2016)11-2893-07

10.11999/JEIT151444

2015-12-22；改回日期：2016-07-08；

2016-09-30

李浩 leo.lihao@163.com

国家自然科学基金(61401511)

The National Natural Science Foundation of China (61401511)

李 浩： 男，1986年生，博士生，研究方向为通信信号处理、盲信号处理.

彭 华： 男，1973年生，教授，研究方向为通信信号处理、软件无线电.