某框架-核心筒结构的pushover分析

李秋喜，李大华，王 帅，张朋仁

（安徽建筑大学 土木工程学院，安徽 合肥　230601）

某框架-核心筒结构的pushover分析

李秋喜，李大华，王 帅，张朋仁

（安徽建筑大学 土木工程学院，安徽 合肥230601）

以某工程为例，运用大型有限元分析软件MIDAS/GEN对框架-核心筒结构进行分析。并通过对层间位移角曲线、层间位移曲线、塑性铰分布状态等方面的模拟计算与分析对结构的抗震性能进行的评估，结果表明该结构在地震力作用下能够满足使用功能要求并分析出楼层薄弱环节，为楼层加固提供依据。

框架-核心筒 ；静力弹塑性分析 ；抗震性能 ；薄弱环节；MIDAS/GEN

0　引　言

框架-核心筒是高层、超高层建筑的主流形式，外框架与核心筒能联合抵制横向作用力，该结构十分有利于结构受力，并具有很好的抗震性［1-2］。当建筑物到达一定的高度后，侧向位移成为结构强度的主要控制因素，为确保建筑物在大震下的稳定性，抗震设计时增加结构的侧向刚度变得尤为重要，而框架-核心筒结构的核心筒恰好具有强大的侧向刚度，弥补了框架柱侧向刚度不足的缺陷。框架-筒体结构中的框架部分地震剪力应进行调整，直至调整后的剪力大于结构底部总地震剪力的20%和按侧向刚度分配的框架部分楼层地震剪力中最大值1.5倍二者的较小值［3］。MIDASGEN是一款大型有限元分析软件，被广泛用于结构抗震设计，下面我们通过软件中的静力弹塑性分析对框架-核心筒结构进行分析，验证结构的抗震性能。

1　工程概况

该工程为一个35层的钢筋混凝土框架-核心筒结构。建筑总高为126 m，标准层层高3.6 m,各标准层构件采取相同位置布置，建筑平面尺寸为32 m×32 m，核心筒尺寸为18 m×16 m，核心筒开洞尺寸为4 m×3 m，标准层布置如图1，主要尺寸表见表1。

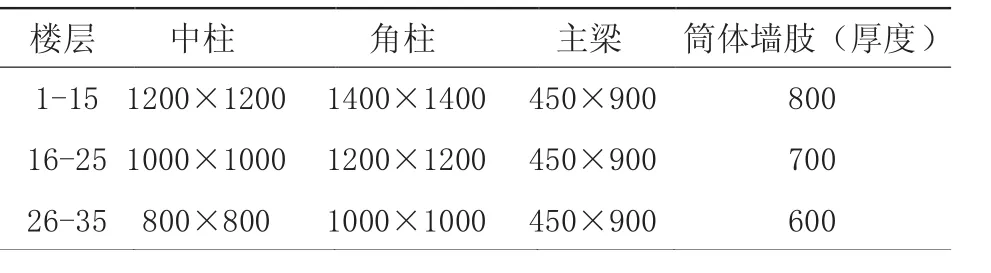
表1　建筑平面尺寸/mm

本工程按7度（0.1 g）进行抗震设防，设计地震分组为第一组，本工程为二类场地土，基本风压为0.35 kN/m²（100年一遇 ），场地特征周期为0.35 s，结构阻尼比取5%，地面粗糙类别为C类 罕遇地震为0.08，罕遇地震为 0.50，楼层恒载5.0 KN/m²，活载3.0 KN/m²。整楼模型如图2所示

图1　标准层

图2　整楼模型

2　静力弹塑性分析

静力弹塑性分析是将地震作用转换为横向静力荷载，然后对结构进行逐步施加单调荷载，直至结构最大位移超出允许位移限值或结构濒临破坏为止的一种非线性分析法［4］。静力弹塑性分析是一种经过简化的近似计算方法，该方法具有受地震波输入不确定性影响较小的优点，被广泛应用于高层结构的抗震性能分析中。在分析前先假定地震力为横向荷载，将假定的横向荷载施加在结构上并逐步增大，最终得到结构基底剪力-顶点位移关系曲线。能力谱法（CSM）、目标位移法（NSP）、和N2方法是常见的pushover分析方法。其原理是一样的，他们主要的不同之处于对结构抗震性能具有不同的评价的方法以及在地震作用下结构目标位移具有不同的确定方法。结构性能点是将某一水准地震的需求谱曲线与横向静力荷载作用下的能力谱曲线在同一坐标系中的交点，通过对结构性能点处各项性能指标进行分析来对结构抗震性能进行综合评定。

Midas/Gen程序中提供了两种方法计算性能点，两种方法原理相同，只是具体的操作不同，运用Procedure-A（图3）方法是可能会不收敛，Procedure-B（图4）方法可以很好的解决这种问题［5］。

图3　Procedure-A

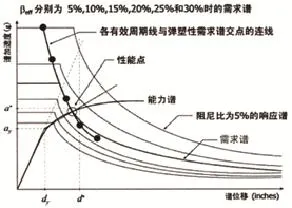
图4　Procedure-B

3　结构性能分析

采用MIDAS/GEN对结构进行静力弹塑性分析，能力谱采用性能点控制（FEMA），性能点评价方法选用 procedure-B，通过假定需求曲线并使用相应的等效周期和等效阻尼比，得到与能力谱相交点。在能力谱推覆曲线中，性能控制点由其中的一条需求谱与能力谱相交形成。

3.1X 方向的静力弹塑性分析

图5　X方向推覆曲线

结构在X方向进行加载，得到罕遇地震下结构的静力弹塑性（pushover）分析曲线，如图5所示。结构在性能点处的谱加速度Sa=0.108 g，谱位移Sd=101.6 mm，性能点位移为165.5 mm，基底剪力为 21320 KN。

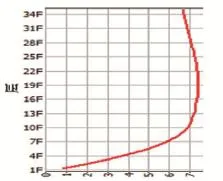
图6　X向层间位移（mm）

图7　X向层间位移角

根据图6、7所示层间位移和层间位移角曲线可以得出，X方向楼层在19层出现最大层间位移7.541 mm，最大层间位移角为1/488出现在19层，均能满足高层建筑混凝土结构技术规程。结构整体设计能做到大震不倒并满足使用要求。

3.2Y 方向的静力弹塑性分析

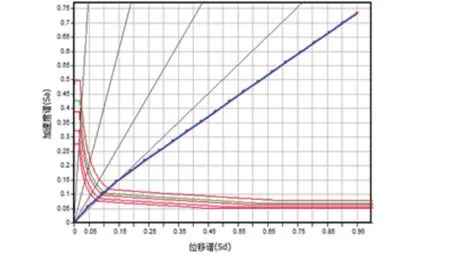
图8　Y方向推覆曲线

采用同样的方法对Y方向施加荷载，得到Y方向的静力推覆曲线，如图8所示。在结构性能点处结构的Sa=0.107 g，谱位移 Sd=100.5 mm，性能点位移为158 mm，基底剪力为18530 KN。

图9　Y向层间位移

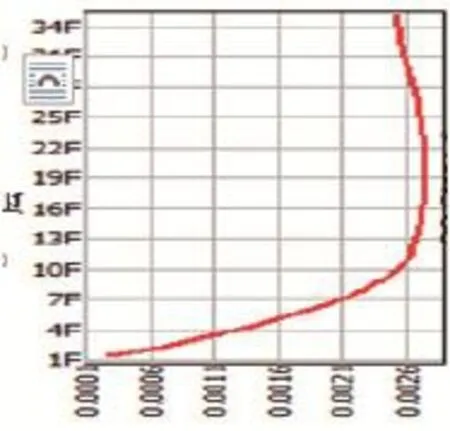
图10　Y向层间位移角

通过对图9和图10进行分析可知，结构在十九层出现最大层间位移与最大层间位移角1/340，满足高层建筑混凝土结构技术规程规定的最大层间位移角限值1/100［6］，结构能够达到使用功能要求。

3.3塑性铰分布

结构遭遇地震后可能出现的状态分为 IO、LS 和 SS （CP）等，状态代表铰的能力水平，在IO状态可以正常使用，在LS阶段有不同程度的损坏需要进行控制，当达到SS（CP）状态时结构严重失稳危害人身财产安全。由图11所示，其中，每个点的横坐标为相应的弹塑性位移限值，B点表示出现塑性铰点，C点表示出现倒塌点［7］。

图11　不同性能水准下的塑性铰弹塑性骨架曲线

4　结论

通过采用大型有限元软件MIDAS/GEN对该35层框架-核心筒结构进行静力弹塑性分析，得到以下结论：

1）通过对该框架-核心筒的静力弹塑性分析得知，该结构层间位移和层间位移角均能满足规范限值，并分析出最大层间位移角出现在结构的第十九层。

2）通过静力弹塑性分析，验证了框架-核心筒结构的双层防线大大提高了结构的抗震性能。

3）静力弹塑性分析能够很好地反应结构破坏机制，能够通过明确反应出结构的薄弱层位置，为设计加固提供了强有力的理论依据。

图12　塑性铰分布

由图12可知虽然结构出现了少量塑性铰，但结构绝大部分还处于弹性阶段，该结构核心筒绝大部分都处于能正常使用的弹性阶段，该结构框架梁几乎不出现塑性铰，塑性铰只在与剪力墙相连的梁端出现。框架柱基本不出现塑性铰，处于能正常居住阶段，由于核心筒有足够大的刚度来抵挡水平剪力，所以柱子几乎只承受竖向作用,因此结构少量的塑性铰出现在框架梁与核心筒相连的一端［8］。以上分析表明框架柱与核心筒分别为抗震设计的两道防线，能够满足大震不倒、中震可修的目标。

［1］陈宇,张明,沈蒲生.带加强层框架—核心筒结构的Pushover分析［J］.工程抗震与加固改造,2008,30 （6）：33-40.

［2］李一昕,陶慕轩,丁然,等.组合框架-核心筒体系抗震性能动力弹塑性分析方法［J］. 建筑结构学报,2015,36（s1）：1-7.

［3］中华人民共和国住房和城乡建设部.JGJ 3—2010高层建筑混凝土结构技术规程［S］.北京：中国建筑工业出版社，2011.

［4］陈佳琪,马克俭,聂世杰,等.钢筋混凝土空间网格盒式“成束筒”结构静力弹塑性分析［J］.贵州大学学报（自然科学版）,2014,31（5）：77-80.

［5］陈健.钢框架—混凝土核心筒结构弹塑性分析［D］.成都：西南交通大学,2013.

［6］GB 50011—2010 建筑抗震设计规范［S］.北京：中国建筑工业出版社,2010.

［7］侯高峰,王建国,张茂.基于MIDAS/GEN高层建筑结构静力弹塑性分析［J］.合肥工业大学学报（自然科学版）,2008,31（10）：1664-1667.

［8］王燕燕,莫海鸿.基于MIDAS-Building的某超限高层建筑静力弹塑性分析［J］.四川建筑科学研究,2012,38（6）：181-185.

Pushover Analysis of a Frame - core Tube Structure

Li Qiuxi,Li Dahua ,Wang Shuai ,Zhang Pengren
（School of Civil engineering, Anhui JianZhu University, Hefei 230601, China）

Taking an engineering as anexample, this paper applies the fnite element analysis software MIDAS/ GEN to make a static elastic-plastic analysis on frame-core tube structure.By Simulation and analysis of interstory drift ratio, inter-story displacement and the distribution of plastic hinge distribution state , this paper aimsto evaluate the structural seismic behavior. The results shows that under seismic action this structure can satisfy application requirement and can determine the weak links in the structureand thus offers foundation for consolidation of the foor.

Frame-core tube structure；pushover analysis；seismic behavior；weak link；MIDAS/GEN

TU312

A

2095-8382（2016）04-013-04

10.11921/j.issn.2095-8382.20160403

2016-01-07

李秋喜（1989—），男，硕士研究生，研究方向：结构工程。