基于稀疏时频分解的盲波束形成算法

陈 沛 赵拥军 刘成城



基于稀疏时频分解的盲波束形成算法

陈 沛*赵拥军 刘成城

(解放军信息工程大学导航与空天目标工程学院 郑州 450001)

针对现有盲波束形成算法通用性差，所需采样数据量大等问题，该文提出一种基于稀疏时频分解的盲波束形成算法。算法首先将传统的短时傅里叶变换转化为稀疏重构问题，利用交替分裂Bregman算法进行迭代求解。然后利用对各阵元的接收信号进行稀疏时频分解的结果，结合聚类和不确定集方法，实现导向矢量的最优估计。最后利用MVDR算法获得最优权矢量。该算法无需利用信号统计特性，实现了高效的盲波束形成。仿真实验结果表明，该算法所需数据量小，迭代步骤易于工程实现，较现有盲波束形成算法输出性能更优，适用范围更广。

盲波束形成；时频分解；稀疏重构；导向矢量估计

1　引言

自适应波束形成技术一直以来是阵列信号处理中的热点和难点，其在雷达、声呐、无线通信以及地震预测、医学诊断等诸多领域均取得到了广泛的应用。传统的自适应波束形成算法一般需要准确已知阵列的导向矢量和目标信号的来向信息，在实际应用中往往受到先验信息不准确的影响，输出性能降低。尽管已有研究通过各类稳健算法，在一定程度上提高了先验信息存在误差情况下的阵列输出性能，但仍无法克服对先验信息的依赖[4,5]。盲波束形成算法由于只需要极少的先验信息而无需训练数据[6]，在各类实际阵列天线系统中的需求最为迫切。

现有的盲波束形成算法通用性较差，一般要求信号具有一定的统计或结构特性，如恒模特性、循环平稳特性，非高斯特性等。其中，恒模约束准则是盲波束形成算法设计中最常用的准则之一，恒模算法(Constant Modulus Algorithm, CMA)利用源信号的恒模特性，对接收期望信号的阵列响应施加约束[7]，再利用随机梯度法等自适应算法进行迭代运算[8]，实现期望信号的增强和干扰抑制。该类算法收敛速度较慢，文献[9]提出基于最小二乘的改进算法，提高了收敛速度，但性能受迭代算法参数设置影响较大。另一类盲波束形成算法基于源信号的循环平稳特性[10]，在理想情况下输出性能较好，但实际应用中源信号准确的循环频率很难获得，且需要较大的数据量。此外，基于独立分量分析(Independent Component Analysis, ICA)的一类盲波束形成算法针对强干扰信号有更好的输出性能，但要求源信号具有非高斯性且满足独立性假设[11]。其中，峭度最大化算法(Kurtosis Maximization Algorithm, KMA)适用于任意非高斯信号[12]，但步长调节参数在信道未知条件下很难选择。基于高阶累积量的盲波束形成算法抗噪声性能好，但计算复杂度高，应用条件较为苛刻[13]。当存在多目标信号时，现有的盲波束形成算法需采用多模块级联或并联的方式，在实际系统中实现难度大，输出性能不高。

文献[14]将时频分解技术引入盲波束形成中，克服了对信号统计特性的严格要求，并且能够实现多目标信号的并行输出，但算法复杂度高，所需数据量大，不利于工程实现。因此，本文从稀疏信号恢复理论出发，设计稀疏时频分解算法，利用较少的数据量得到更准确的阵列接收信号时频分解结果，再通过对属于同一源信号的时频点聚类，并结合不确定集思想，实现导向矢量的准确估计，进而利用MVDR算法实现多目标信号的盲波束形成。该算法所需信号采样快拍数更少，收敛速度更快，仿真实验和结果分析将证明该算法的有效性和稳健性。

2 信号模型

考虑一个元均匀直线阵列，有个互不相关的窄带独立点源从远场空间以平面波形式入射，最大波长为，阵元间距设置为半波长。信号入射的方位角表示为,。时刻的阵列接收采样快拍矢量表示为

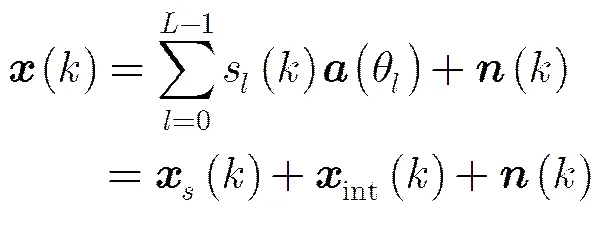
(2)

(3)

阵列的输出信干噪比(Signal-to-Interference- plus-Noise Ratio, SINR)定义为[4]

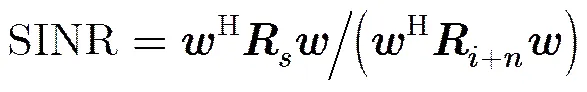
(5)

传统的最小方差无畸变(Minimum Variance Distortionless Response, MVDR)波束形成算法以最大化SINR为目标，求解式(6)所示优化问题。

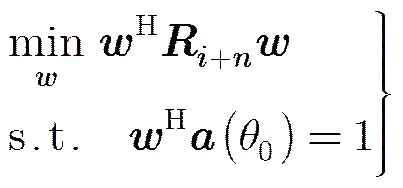
利用Lagrange乘数法可得最优权矢量为[15]

(7)

但在实际应用中，由于难以得到理想的干扰加噪声协方差矩阵，常用采样协方差矩阵代替，如式(8)所示。

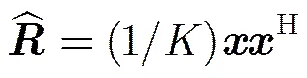
通过上述结论可以看出，传统的波束形成算法需要可靠的信号来向等先验信息，以获得准确的导向矢量。盲波束形成算法无需已知信号来向，直接得到导向矢量的估计，进而实现最优权矢量的求取。

3 基于稀疏时频分解的盲波束形成

时频分析技术是电磁信号处理中的一类基本手段，为了保证较高的时间分辨率和频率分辨率，时频分析所需数据量大，计算复杂度高，限制了其在实际系统中的应用。近年来，随着稀疏信号恢复技术的发展，当信号满足稀疏性条件时，可以通过少量观测数据实现对原始信号的精确恢复。在阵列信号处理中，接收信号在时频域中能够满足稀疏性条件[16]，因此本文考虑采用稀疏恢复与时频分析相结合的稀疏时频分解法，实现较少数据量和较低计算复杂度下的高精度信号时频分解，并进一步实现盲波束形成。

3.1 基于Bregman 迭代的稀疏时频分解

短时傅里叶变换(Short-Time Fourier Transform, STFT)是一种基本的时频分析方法，针对能量有限信号进行分解，其时频域表达式可表示为

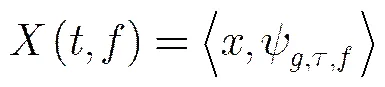
STFT通常以离散形式得到对信号时频域的网格化采样[17]，则考虑第个阵元接收信号的采样，得到离散形式,，其中，表示采样间隔，对于一个给定的窗函数，则接收信号的时频分解可表示为

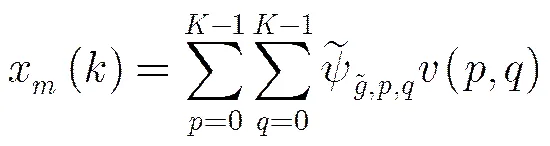
由于STFT是一种线性变换[17]，可将变换式(10)表达为矩阵形式，如式(11)所示。

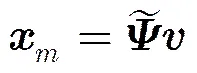
(12)

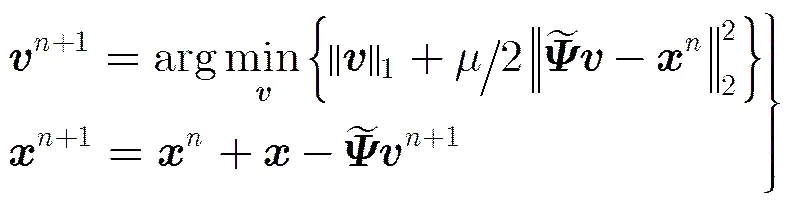
(14)

表1 基于Bregman迭代的稀疏时频分解步骤

初始化：。迭代步骤：收敛条件：输出：

(15)

3.2 导向矢量估计

由于任意两不同来向信号的导向矢量线性无关，因此，若时频分解所得的时频点仅由单个源信号产生，可利用该类时频点进行导向矢量估计。具体地，暂不考虑噪声，对每个阵元的接收信号进行时频变换，可得

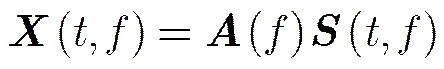
(17)

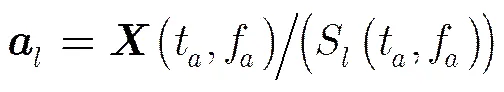
(19)

因此，对各阵元的接收信号进行时频分析后，可将各个时频点上求得的作为该时频点的特征矢量。在此基础上利用聚类算法，对所有时频点进行分类，这里采用若满足，则属于同一类的准则，其中

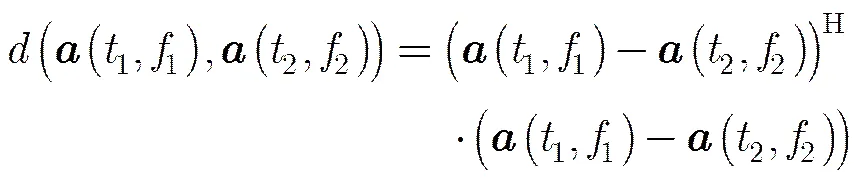
(21)

式(21)是一个凸优化问题，可运用内点法求解。文献[23]也提出了相应的简化求解算法，可在实际应用中予以考虑。

3.3 波束形成

将利用式(21)得到的各源信号的导向矢量估计值分别代入式(6)中，如式(22)所示。

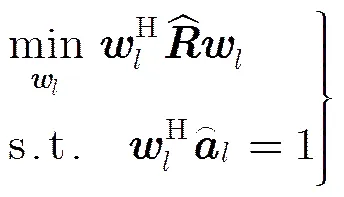
利用Lagrange乘数法对式(22)求解，可得到分别以各源信号为期望信号进行波束形成的最优权矢量为

(23)

综上所述，基于稀疏时频分解的盲波束形成算法步骤总结如表2所示。

表2 基于稀疏时频分解的盲波束形成算法步骤

初始化：设置常数，滑动窗长度，最大迭代次数N。步骤1 利用基于Bregman迭代的稀疏时频分解得到各个阵元接收信号的时频分布矩阵。步骤2 通过式(21)求得期望信号导向矢量的估计值。步骤3 通过式(23)求得加权系数，实现波束形成。输出：。

3.4 算法分析

噪声条件下，为提取单个源信号产生的时频点，需设置合理阈值，仅保留幅度较大的时频点。另一方面，当多个信号在时频域产生交叠，交叠位置上的幅度过大的时频点也应通过设置阈值除去。相应阈值的设置可根据实际应用环境灵活调整。此外，上述算法描述中，为便于说明，聚类部分要求已知信源数目，当信源数目未知时，可采用无需已知分类数的聚类算法[24]。值得指出的是，尽管本文算法对相干信号有一定的处理能力，但推导步骤没有针对相干信号进行分析，本文仍着重于考虑信源独立的一般条件。

与文献[14]算法相比，计算复杂度的主要差距在于本文算法进行稀疏时频分解的迭代步骤。分析迭代步骤，由于矩阵具有对角阵形式，其求逆运算的复杂度很低，矩阵的构造可以通过次点逆傅里叶变换快速实现，而clip函数的计算复杂度也很低。因此，每次迭代的主要计算复杂度为，较文献[14]算法更低，对比如表3所示。

表3 计算复杂度分析

算法类型计算复杂度 本文算法 文献[14]算法

4 仿真结果与分析

考虑一个10阵元均匀直线阵，阵元间距设置为载波波长的一半，为不失一般性，3个远场窄带线性调频信号分别从,,3个角度入射，调频范围分别为600~610 MHz, 605~615 MHz, 615~605 MHz(频率递减)，相互独立，信号带宽均为10 MHz, 相对带宽满足窄带条件。采样频率为50 MHz，信号输入信噪比均为10 dB。设置仿真实验对本文算法性能进行分析，并将本文算法与CMA算法，KMA算法，高阶累积量算法以及利用传统STFT的盲波束形成算法进行对比。

实验1 阵列响应性能分析 本实验中设置接收信号采样快拍数为50，稀疏时频分解算法的窗函数长度设置为11,,，最大迭代次数为100。分别将3个入射信号作为期望信号，本文所提盲波束形成算法得到的阵列响应波束图如图1所示。从图1中可以看到，在各信号强度相同，信号形式相近的条件下，本文算法所形成的3个阵列响应波束图的主波束均能准确指向期望信号来向，而将另外两个信号视作干扰信号并在其入射方向上形成较深的零陷，从而可以实现信号的有效分离。由于本文算法中，3个入射信号的导向矢量估计可以同时得到，因此以每个信号为期望信号进行波束形成的过程可以并行实现，从而实现接收信号的高效分离。而在入射信号相近的条件下，CMA算法，KMA算法，高阶累积量算法难以同时实现3个信号的有效分离。

通过仿真结果可以看到，在整个期望信号SNR变化范围内，本文稀疏STFT算法相较于CMA算法，KMA算法，高阶累积量算法达到了更好的输出性能，而由于采样数据量的不足影响了传统STFT盲波束形成算法的时频分解性能，使得其对导向矢量的估计不再准确，从而导致输出性能有所下降。

再将期望信号SNR固定为10 dB，采样快拍数变化范围设置为，步长为5，其他条件不变，比较算法输出SINR随采样快拍数变化关系，仿真结果如图3所示。从图3中可以看到，与现有算法相比，本文算法仅需要较少的采样快拍数，就能达到较高的输出性能，快拍数达到30个以上时，输出SINR已能够接近理想值。现有的各类盲波束形成算法在采样数据不足的条件下，输出性能均下降明显，其要达到可靠的输出性能，均需要大量的采样数据。

综上所述，本文算法相对于现有算法在输出性能和数据量需求方面有着较为明显的优势。

实验3算法稳健性分析 考虑本文算法的稳健性，在阵列流型矢量建模中引入幅相误差矢量，为每个阵元在通道内增加幅相扰动，即，其中，。令,分别在和的均匀分布中随机选取，其他仿真条件与实验2一致。分别比较各算法输出SINR随期望信号SNR的变化关系，以及随采样快拍数的变化关系，仿真结果如图4和图5所示。

通过仿真结果可以看到，当存在通道误差时，各算法输出性能均有所降低，这是由于幅相扰动使得估计所得导向矢量与理想条件下导向矢量的差异增大，干扰方位零陷变浅，对干扰信号抑制能力降低。但在较大的期望信号SNR变化范围和较少的快拍数条件下，本文算法相比现有算法仍有优势。

通过图6可以看到，窗长过窄或过宽均会引起盲波束形成算法输出性能的降低。当窗长过窄时，局部频谱的分辨率降低，使得时频分解结果的频域分辨率降低，各个阵元接收信号的时频分布矩阵中可用于导向矢量估计的单源时频点减少，从而影响导向矢量估计准确度。当窗长过宽时，窗宽超过非平稳信号的局域平稳长度，窗函数内的局部频谱表现不再准确，将影响单源时频点的准确聚类，同样会影响导向矢量的估计。实际应用中，窗长度可根据实测环境进行离线选取。

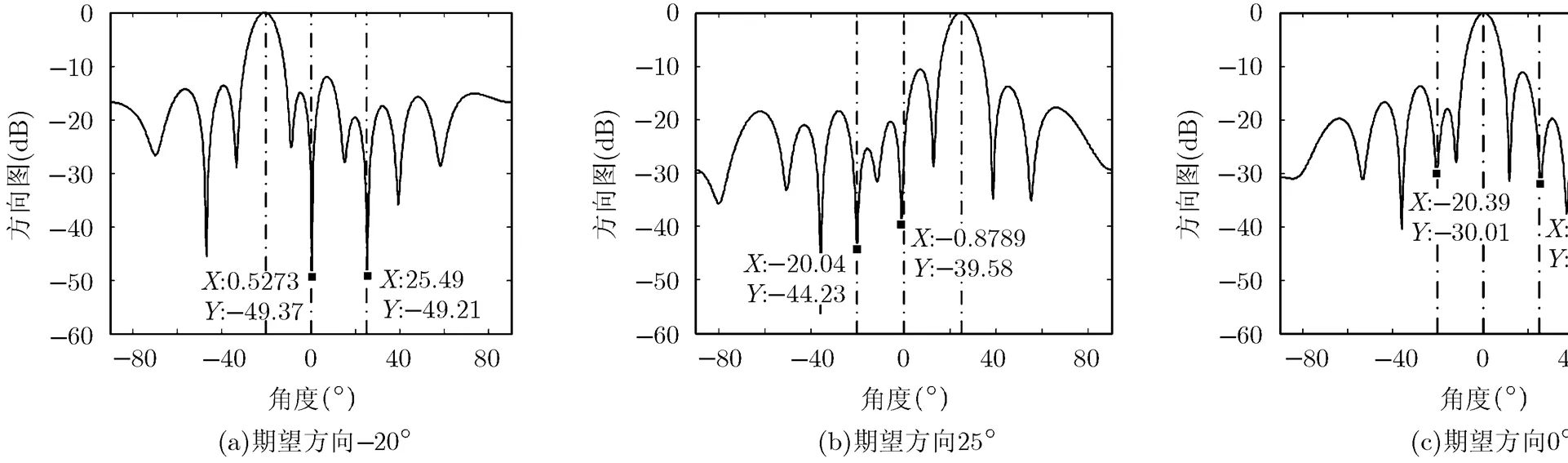
图1 本文算法阵列响应波束图

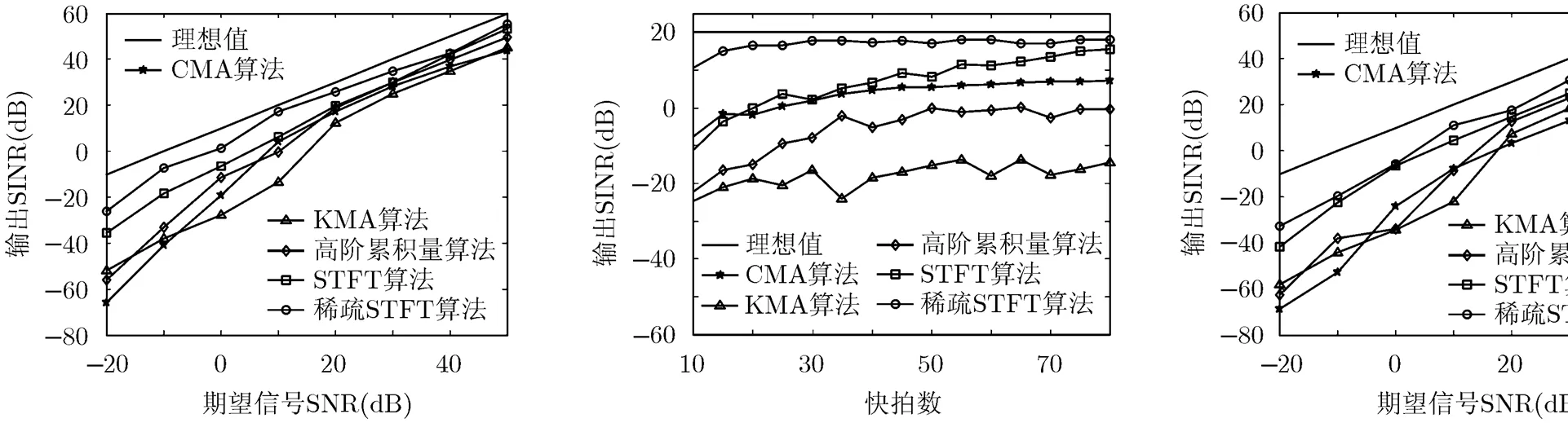
图2 各算法输出SINR随期望信号SNR变化关系  图3 各算法输出SINR随采样快拍数的变化关系  图4 误差条件下输出SINR随期望信号SNR变化关系

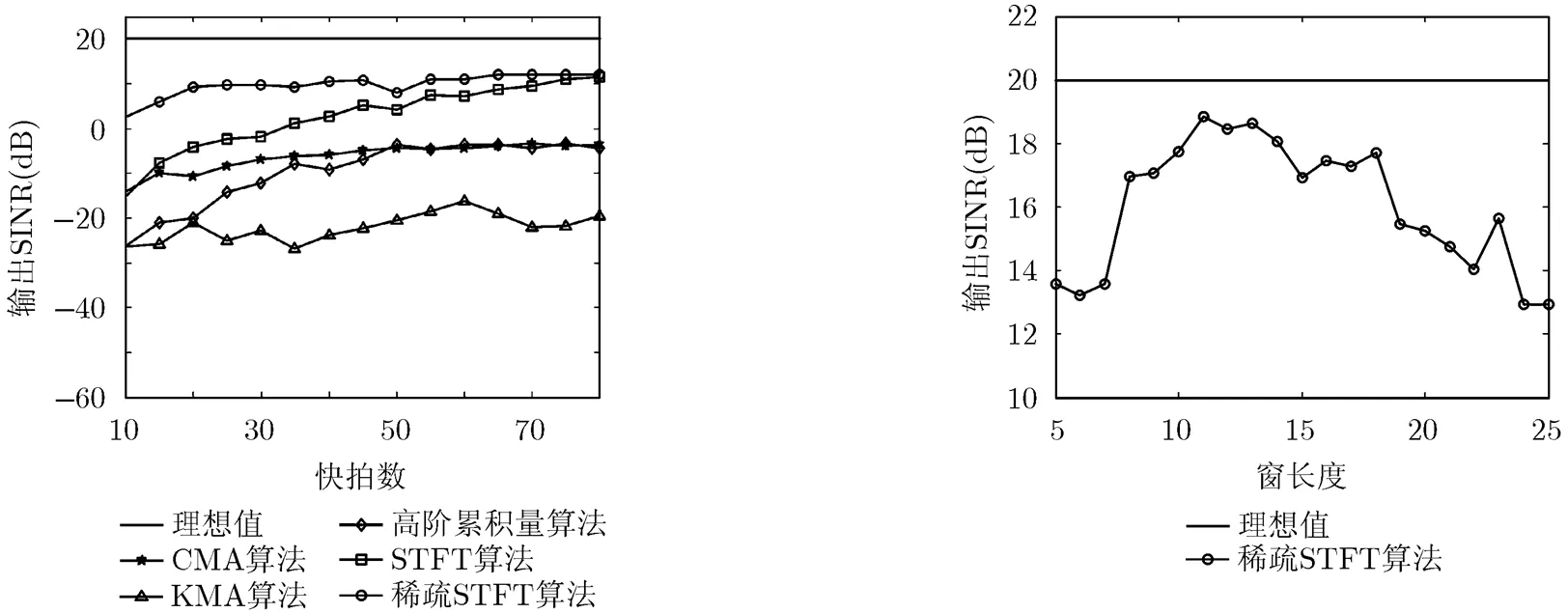
图5 误差条件下输出SINR随采样快拍数的变化关系     图6 输出SINR随窗长度的变化关系

5 结论

针对现有盲波束形成算法通用性差，输出性能不高等问题，本文通过引入稀疏时频分解，无需利用信号统计特性，实现了高效的盲波束形成算法。算法首先将传统的STFT算法转化为一个综合范数和范数的稀疏优化问题，随后利用交替分裂Bregman算法进行迭代求解，实现分辨率可调节的稀疏时频分解。进而利用对各阵元的接收信号进行稀疏时频分解的结果，结合聚类和不确定集方法，实现导向矢量的最优估计。最后利用MVDR算法获得最优权矢量。仿真实验结果表明，本文算法所需数据量更小，运算复杂度较低，迭代步骤更易于工程实现，相比现有盲波束形成算法输出性能更优，适用范围更广。

参考文献

[1] 李立欣, 白童童, 张会生, 等. 改进的双约束稳健Capon波束形成算法[J]. 电子与信息学报, 2016, 38(8): 2014-2019. doi: 10.11999/JEIT151213.

LI Lixin, BAI Tongtong, ZHANG Huisheng,. Improved double constraint robust capon beamforming algorithm[J].&, 2016, 38(8): 2014-2019. doi: 10.11999/JEIT151213.

[2] SHEN Feng, CHEN Fengfeng, and SONG Jinyang. Robust adaptive beamforming based on steering vector estimation and covariance matrix reconstruction[J]., 2015, 19(9): 1636-1639. doi: 10.1109/LCOMM.2015.2455503.

[3] 黄岩, 廖桂生, 李军, 等. 基于连续差联合阵列的非等距线阵无模糊波束形成方法[J]. 电子与信息学报, 2015, 37(12): 2891-2897. doi: 10.11999/JEIT150321.

HUANG Yan, LIAO Guisheng, LI Jun,. Non-ambiguity beamforming of nonuniform linear array based on consecutive difference coarray[J].&, 2015, 37(12): 2891-2897. doi: 10.11999/ JEIT150321.

[4] GU Yujie and LESHEM A. Robust adaptive beamforming based on interference covariance matrix reconstruction and steering vector estimation[J]., 2012, 60(7): 3881-3885. doi: 10.1109/TSP.2012. 2194289.

[5] ZHANG Zhenyu, LIU Wei, LENG Wen,. Interference- plus-noise covariance matrix reconstruction via spatial power spectrum sampling for robust adaptive beamforming[J]., 2016, 23(1): 121-125. doi: 10.1109/LSP.2015.2504954.

[6] COVIELLO C M and SIBUL L H. Blind source separation and beamforming: algebraic technique analysis[J]., 2004, 40(1): 221-235. doi: 10.1109/TAES.2004.1292155.

[7] XU Changjiang, FENG Guangzeng, and KYUNG K S. A modified constrained constant modulus approach to blind adaptive multiuser detection[J]., 2001, 49(9): 1642-1648. doi: 10.1109/26. 950350.

[8] CAI Yunlong, RODRIGO C D L, ZHAO Minjian,. Low- complexity variable forgetting factor mechanism for blind adaptive constrained constant modulus algorithms[J]., 2012, 60(8): 3988-4002. doi: 10.1109/TSP.2012.2199317.

[9] SONG Xin, WANG Jinkuan, LI Qiuming,. Robust least squares constant modulus algorithm to signal steering vector mismatches[J]., 2013, 68(1): 79-94. doi: 10.1007/s11277-011-0440-2.

[10] WU Qiang and WONG K M. Blind adaptive beamforming for cyclostatioanary signals[J]., 1996, 44(11): 2757-2767. doi: 10.1109/78.542182.

[11] 赵立权. ICA算法及其在阵列信号处理中的应用研究[D]. [博士论文], 哈尔滨工业大学, 2009: 1-18.

ZHAO Liquan. Research on ICA algorithm and its application in array signal processing[D]. [Ph.D. dissertation], Harbin Engineering University, 2009: 1-18.

[12] 赵立权, 杨莘元, 贾雁飞, 等. 针对任意非高斯信号的快速固定点盲波束形成方法[J]. 系统工程与电子技术, 2009, 31(7): 1577-1580. doi: 10.3321/j.issn:1001-506X.2009.07.012.

ZHAO Liquan, YANG Shenyuan, JIA Yanfei,. Fast fixed point blind beamforming algorithm for arbitrary non- gaussian signals[J]., 2009, 31(7): 1577-1580. doi: 10.3321/j.issn:1001-506X.2009. 07.012.

[13] JAFARI M G, WANG Wenwu, CHAMBERS J A,. Sequential blind source separation based exclusively on second-order statistics developed for a class of periodic signals[J]., 2006, 54(3): 1028-1040. doi: 10.1109/TSP.2005.863005.

[14] 刘亚奇, 刘成城, 赵拥军, 等. 基于时频分析的多目标盲波束形成算法[J]. 物理学报, 2015, 64(11): 114302. doi: 10.7498/ aps.64.114302.

LIU Yaqi, LIU Chengcheng, ZHAO Yongjun,. A blind beamforming algorithm for multitarget signals based on time- frequency analysis[J]., 2015, 64(11): 114302. doi: 10.7498/aps.64.114302.

[15] 李文兴, 毛晓军, 孙亚秀. 一种新的波束形成零陷展宽算法[J]. 电子与信息学报, 2014, 36(12): 2882-2888. doi: 10.3724/SP.J. 1146.2013.02018.

LI Wenxing, MAO Xiaojun, and SUN Yaxiu. A new algorithm for null broadening beamforming[J].&, 2014, 36(12): 2882-2888. doi: 10.3724/SP.J.1146.2013.02018.

[16] JOKANOVIC B and AMIN M. Reduced interference sparse time-frequency distributions for compressed observations[J]., 2015, 63(24): 6698-6709. doi: 10.1109/TSP.2015.2477056.

[17] 张贤达. 现代信号处理[M]. 第2版, 北京: 清华大学出版社, 2002: 349-367.

ZHANG Xianda. Modern Signal Processing[M]. Second Edition, Beijing: Tsinghua University Press, 2002: 349-367.

[18] GHOLAMI A. Sparse time-frequency decomposition and some applications[J]., 2013, 51(6): 3598-3604. doi: 10.1109/TGRS. 2012.2220144.

[19] SCHNASS K and VANDERGHEYNST P. Dictionary preconditioning for greedy algorithms[J]., 2008, 56(5): 1994-2002. doi: 10.1109/ TSP.2007.911494.

[20] CHEN Liwen, ZHENG Jiansheng, SU Mingkun,. A novel beamforming technique: Introducing a convex constrained optimization and compressed-sensing model[J]., 2016, 58(4): 48-59. doi: 10.1109/MAP.2016.2569476.

[21] ZOU Jian, FU Yuli, ZHANG Qiheng,. Split Bregman algorithms for multiple measurement vector problem[J]., 2015, 26(1): 207-224. doi: 10.1007/s11045-013-0251-6.

[22] HUANG Lei, ZHANG Jing, XU Xu,. Robust adaptive beamforming with a novel interference-plus-noise covariance matrix reconstruction method[J]., 2015, 63(7): 1643-1650. doi: 10.1109/TSP. 2015.2396002.

[23] LI Jian, STOICA P, and WANG Zhisong. On robust capon beamforming and diagonal loading[J]., 2003, 51(7): 1702-1714. doi: 10.1109/TSP. 2003.812831.

[24] LUO Yuhui, WANG Wenwu, CHAMBERS J A,. Exploitation of source nonstationarity in underdetermined blind source separation with advanced clustering techniques [J]., 2006, 54(6): 2198-2212. doi: 10.1109/TSP.2006.873367.

陈 沛： 男，1989年生，博士生，研究方向为阵列信号处理.

赵拥军： 男，1964年生，教授，研究方向为新体制雷达系统、阵列信号处理.

刘成城： 男，1986年生，讲师，研究方向为数字波束形成技术.

Blind Beamforming Algorithm Based on Sparse Time-frequency Decomposition

CHEN Pei ZHAO Yongjun LIU Chengcheng

(,450001,)

A novel blind beamforming algorithm based on sparse Time-Frequency Decomposition (TFD) is proposed to solve the problems of existing blind beamforming algorithms: poor universality and the requirement of large amount of sampling data. In the proposed algorithm, the traditional Short-Time Fourier Transform (STFT) is first formulated as a sparse reconstruction problem. Then, a fast and efficient algorithm based on the alternating split Bregman technique is utilized to carry out the optimization. By combining the clustering and uncertainty set methods, the sparse-TFD results of the receiving data at each sensor are used to realize the estimation of Steering Vectors (SV). Finally, the optimal weight coefficients are achieved by substituting the estimated SV into the MVDR beamformer. The proposed algorithm hardly needs any specific statistical property of the receiving signals. Simulation results demonstrate that this algorithm can achieve superior output performance over the existing blind beamforming methods. It needs few snapshots with lower computational cost and has fast convergence rate, which makes the algorithm easy to utilize in practical applications.

Blind beamforming; Time-frequency decomposition; Sparse reconstruction; Steering vector estimation

TN911.7

A

1009-5896(2016)12-3078-07

10.11999/JEIT160995

2016-09-29；改回日期：2016-12-05；

2016-12-13

陈沛 clevercpei@126.com

国家自然科学基金(61401469)

The National Natural Science Foundation of China (61401469)