高性能时不变LDPC卷积码构造算法研究
穆丽伟 刘星成 张 涵
高性能时不变LDPC卷积码构造算法研究
穆丽伟*①②刘星成③张 涵①②
①(华南师范大学物理与电信工程学院 广州 510006)②(华南师范大学广东省量子调控工程与材料重点实验室 广州 510006)③(中山大学电子与通信工程系 广州 510006)
该文基于由QC-LDPC码获得时不变LDPC卷积码的环同构方法,设计了用有限域上元素直接获得时不变LDPC卷积码多项式矩阵的新算法。以MDS卷积码为例,给出了一个具体的构造过程。所提构造算法可确保所获得的时不变LDPC卷积码具有快速编码特性、最大可达编码记忆以及设计码率。基于滑动窗口的BP译码算法在AWGN信道上的仿真结果表明,该码具有较低的误码平台和较好的纠错性能。
LDPC卷积码;有限域;快速编码;时不变;最大编码记忆
1 引言
众所周知,卷积码主要用于实时通信系统,然而,由于Viterbi译码算法的高复杂性,一般情况下仅使用具有较小约束长度的卷积码。近年来,LDPC卷积码[1,2]引起了研究人员的关注。与LDPC分组码一样,LDPC卷积码也由稀疏奇偶校验矩阵定义;但与LDPC分组码不同的是,它们可对输入码流进行连续编译码。在发送端,可用基于移位寄存器的编码器对输入信息流进行连续编码;在接收端,可用基于置信传播(Belief Propagation, BP)译码算法的滑动窗口译码器对从信道接收的码流进行连续译码[3]。而且,与LDPC分组码相比,它们还具有更好的译码性能[1]。LDPC卷积码,因具有比LDPC分组码更好的译码性能[1],比Viterbi更简单的BP译码算法,以及能对输入码流进行连续编译码的特性,而有更好的应用价值,比如,适用于Ethernet。除此之外,印度空间研究组织(Indian Space Research Organization, ISRO)已经开发出了用于全球导航卫星系统(Global Navigation Satellite System, GNSS) 的LDPC 卷积码的MATLAB 和C++模块。美国、俄罗斯、欧盟、中国、日本、印度、尼日利亚及许多其他国家正在频带1559~1610 MHz(L1频带)、1215~1300 MHz(L2频带)以及1164~1215 MHz(L5频带)上计划/开发GNSS。每个系统的信息和数据结构都各不相同,数据率变化范围为25 bit/s到500 bit/s。码率=1/2,信息长度=7 的卷积码已被推荐用于不同信息的前向纠错技术(Forward Error Correction, FEC)中。利用该编码方案的FEC 技术可用于深空通信、光纤通信以及计算机间的通信等。
LDPC卷积码主要有两种结构:具有随机结构的码[4]和具有固定结构的码。后者又称为时不变LDPC卷积码,因具有规则结构并能减少系统实现复杂度而受到学者的广泛关注,其奇偶校验矩阵可由单项式或多项式构成。文献[5]介绍了一种获得时不变LDPC卷积码奇偶校验矩阵的方法。然而,根据文献[5]的分析,由单项式构成的具有更好的环特性,这种结构可由准循环LDPC(Quasi-Cyclic LDPC, QC-LDPC)分组码或随机搜索算法[11,12]获得,显然,由QC-LDPC分组码获得的构造算法更简单。
本文根据由QC-LDPC分组码获得LDPC卷积码的方法,提出用有限域元素直接获得LDPC卷积码的由单项式组成的奇偶校验矩阵的算法,并举例给出了一种用截短的最大距离可分(Maximum- Distance Separable, MDS)卷积码获得的具体构造。到目前为止,几乎所有时不变LDPC卷积码的构造算法主要考虑其译码性能上的优异性,而忽视了其实现上的便利性,更没有考虑LDPC卷积码本身的一个特有优势:快速编码特性。本文算法旨在获得兼具快速编码特性与优异译码性能的时不变LDPC卷积码。该构造算法还具有任意时刻上的最大可达编码记忆以及结果码率与设计码率相等的特性。仿真结果表明,本文提出的时不变LDPC卷积码在小的约束长度下就具有很好的译码性能。
2 时不变LDPC卷积码的奇偶校验矩阵
2.1具有快速编码的LDPC卷积码的二元矩阵
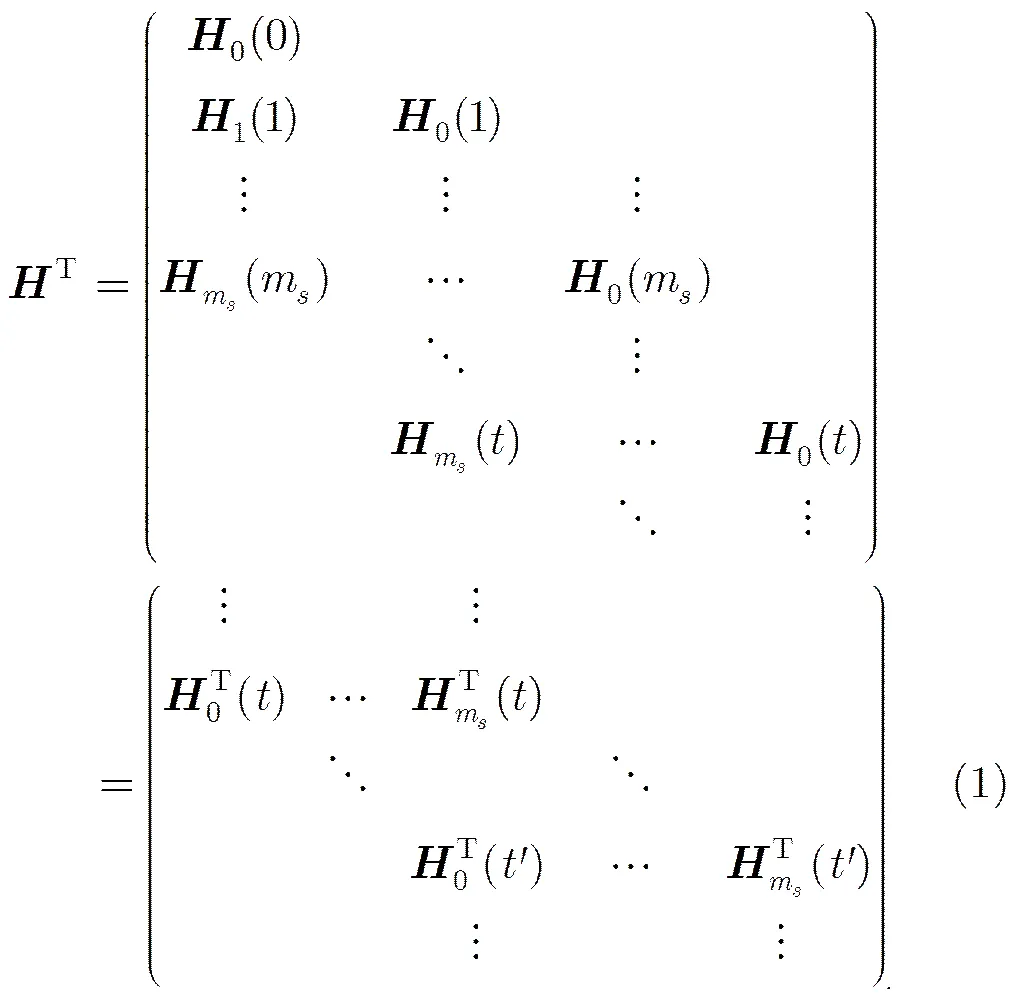
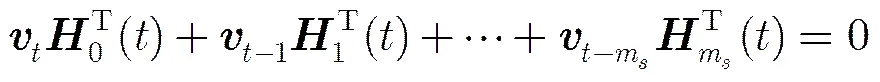
2.2具有快速编码的时不变LDPC卷积码的多项式矩阵
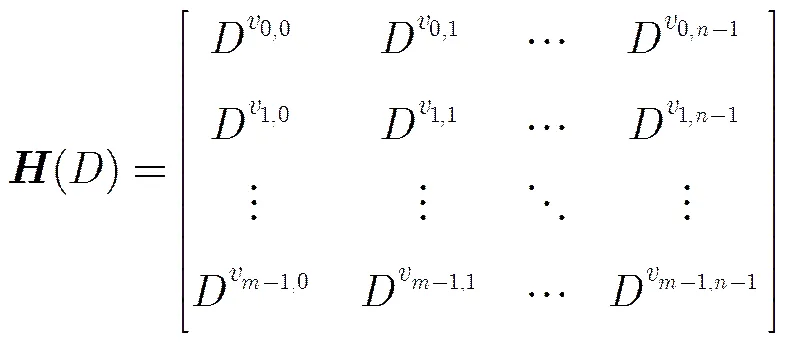
3 构造前准备:在有限域上构造时不变LDPC卷积码的多项式矩阵
本节回顾文献[13]用QC-LDPC分组码获得时不变LDPC卷积码的构造过程,提出在有限域上直接获得时不变LDPC卷积码多项式矩阵的方法。
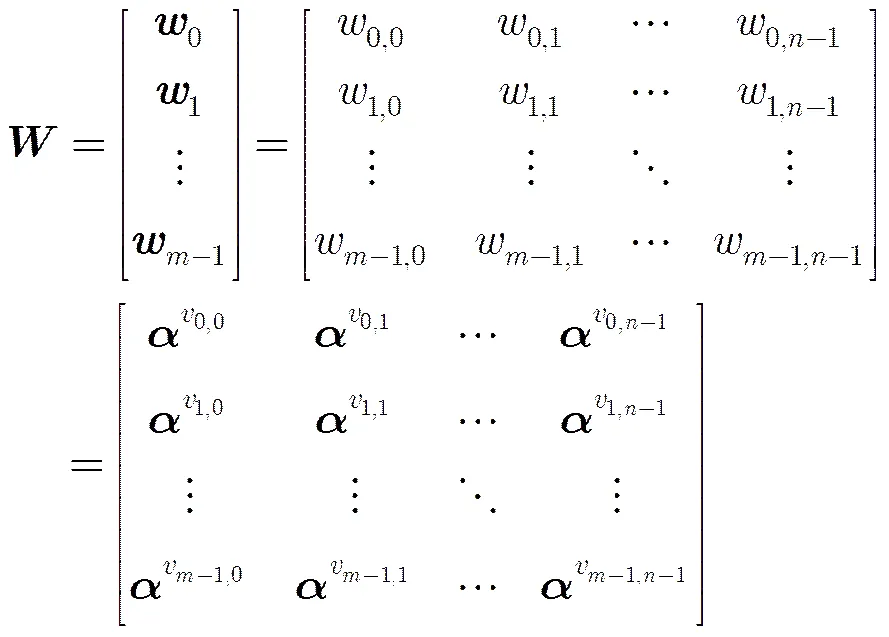
(4)
根据环同构,由式(4)可获得时不变LDPC卷积码多项式矩阵:
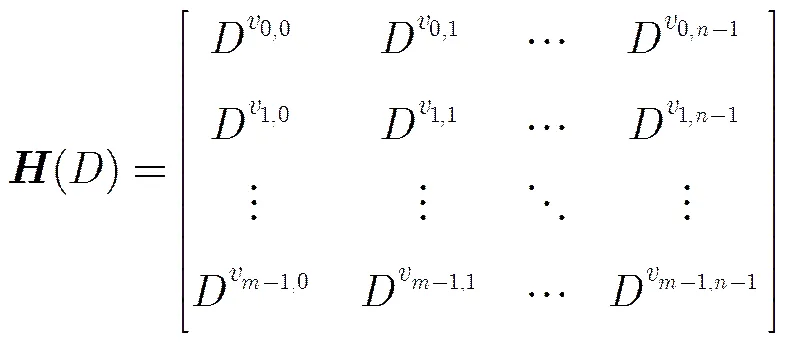
4 构造具有快速编码的时不变LDPC卷积码多项式矩阵
本节根据LDPC卷积码的两个独有特性:(1)快速编码特性,(2)译码性能与编码记忆成正比的特性[1];设计具有快速编码特性及最大可达编码记忆的LDPC卷积码多项式矩阵模型,并以MDS卷积码为例,给出获得该矩阵模型的具体构造方法。
4.1建立矩阵模型
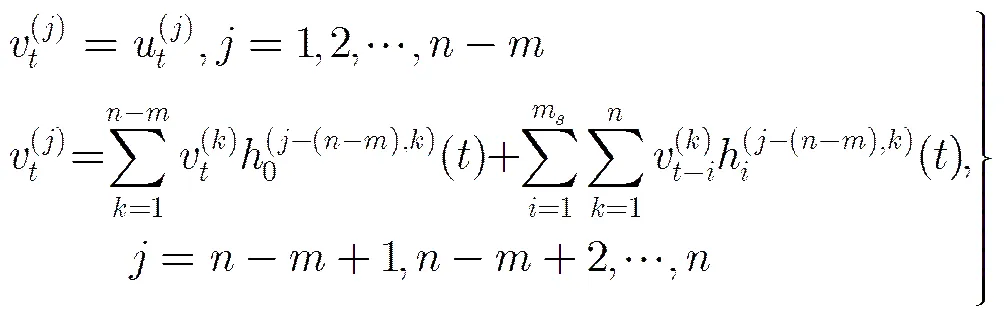
根据二元矩阵与多项式矩阵之间的关系,由式(6)可知令矩阵()最后列对角线上元素为,可确保快速编码特性;令矩阵()前列对角线上元素为,可确保每个编码时刻都有最大编码记忆(具体取值见4.2节),此时,校验模型记忆,多项式矩阵()可表示为

该矩阵可确保时不变LDPC卷积码具有快速编码特性和每个编码时刻上的最大可达编码记忆。
4.2构造算法
(5)所有码字重量(码字中非零码元个数)为。
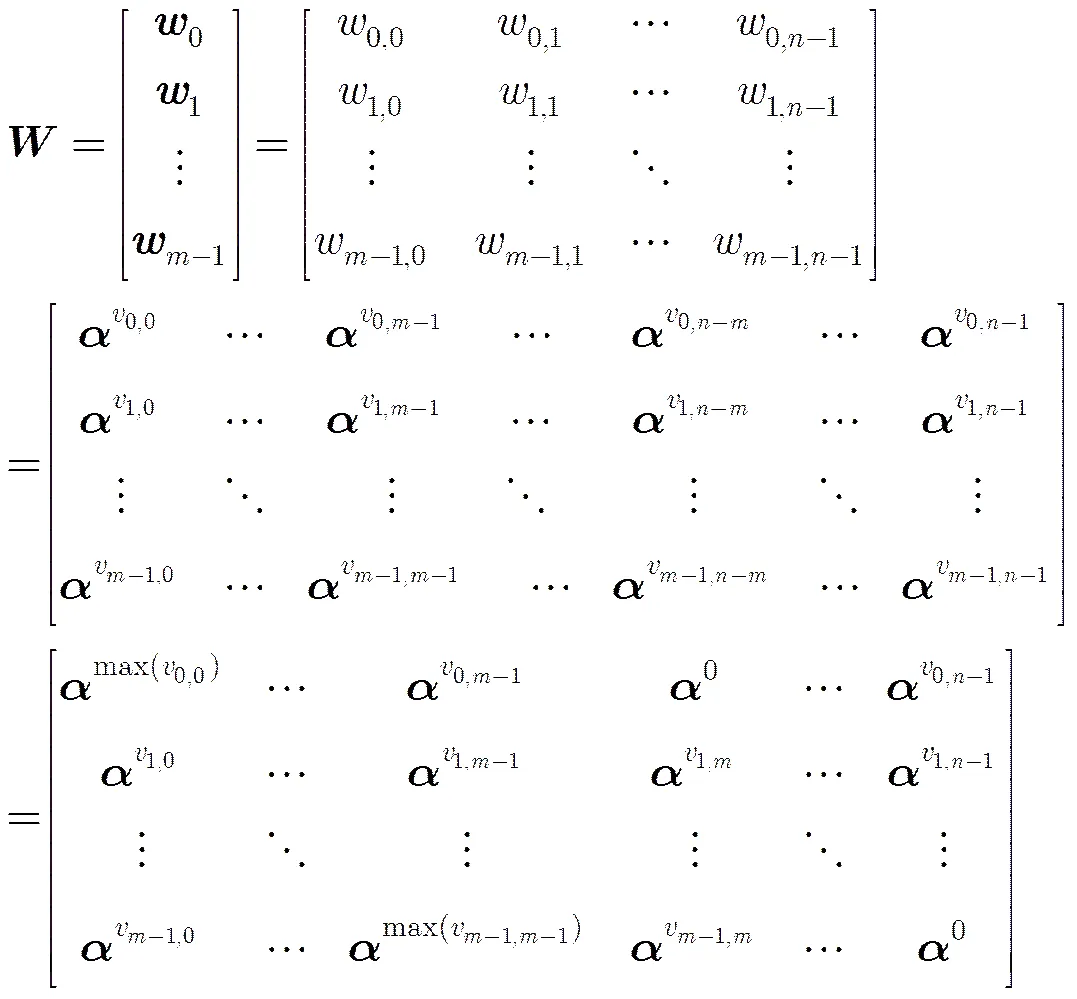
该矩阵具有下列特性:
因为由MDS码生成的QC-LDPC分组码具有更好的性能[15],本节考虑用码率为1/的截短MDS卷积码[15]的部分码字作为LDPC卷积码基矩阵的行元素,并给出一个具体的构造例子。
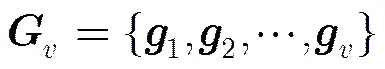
其中,满足约束条件:
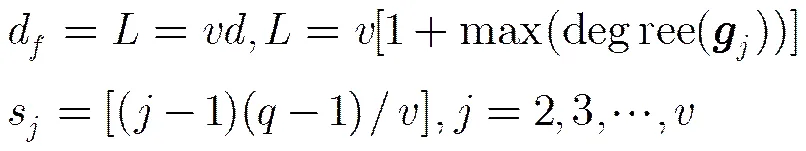
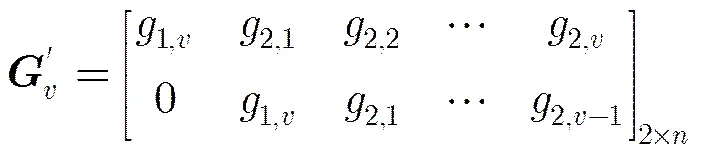
5 数值结果
本节用4.3节的方法构造生成LDPC卷积码及其对应的QC-LDPC分组码并进行性能仿真。用符号()表示码率为的LDPC卷积码,-校验模型记忆,-多项式矩阵行数,-多项式矩阵列数。用符号表示QC-LDPC分组码,-变量节点数,-校验节点数。为了进行性能比较,本文假设LDPC卷积码和QC-LDPC分组码的译码算法具有相同的处理器复杂度,即,分组码的分组长度和卷积码的约束长度相同:。仿真在AWGN信道下进行,最大迭代次数为50,采用文献[1]介绍的BP译码算法对LDPC卷积码及其相应的QC-LDPC分组码进行仿真。
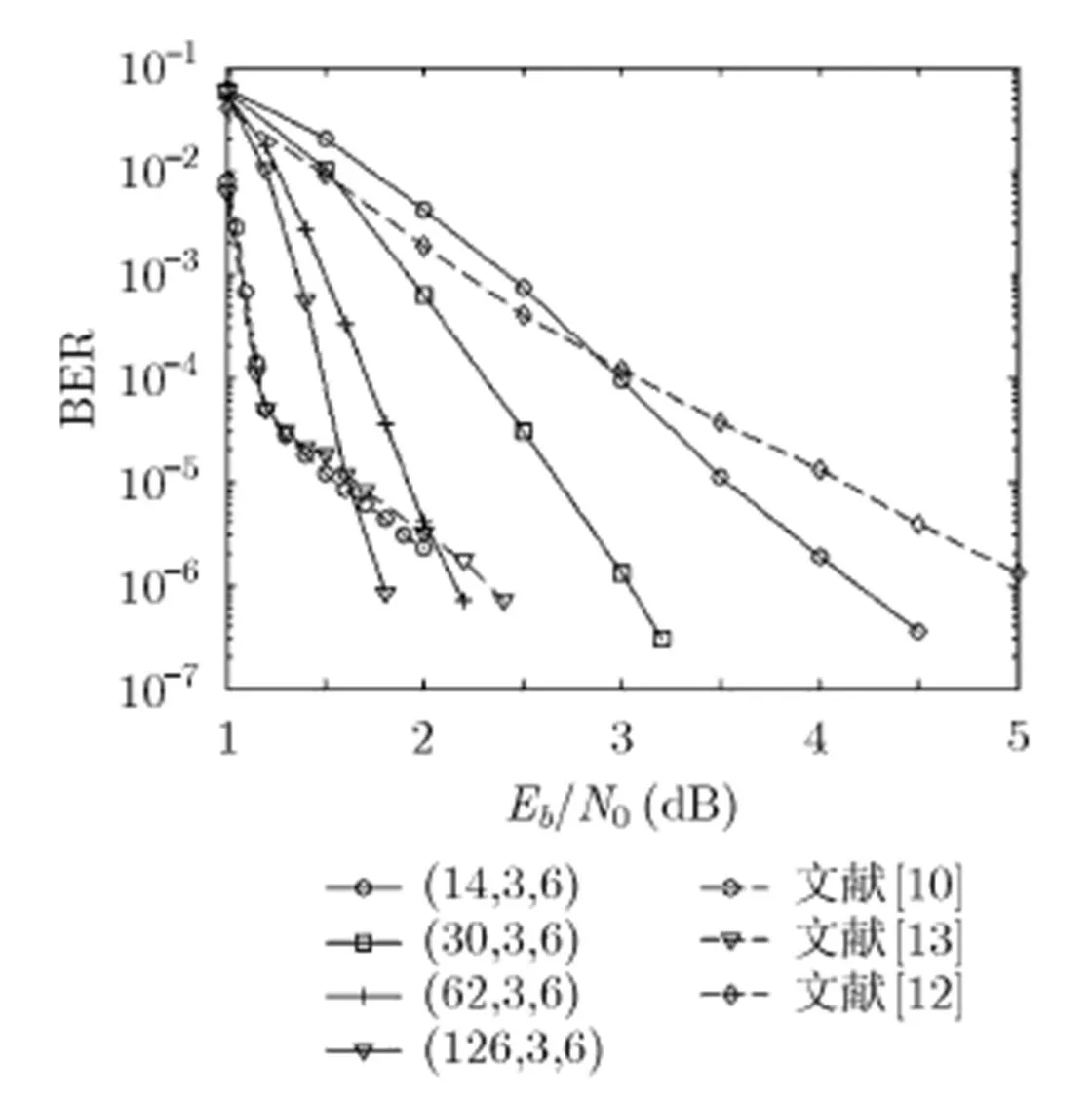
图1 有限域GF(24), GF(25), GF(26)和GF(27)上的LDPC卷积码性能
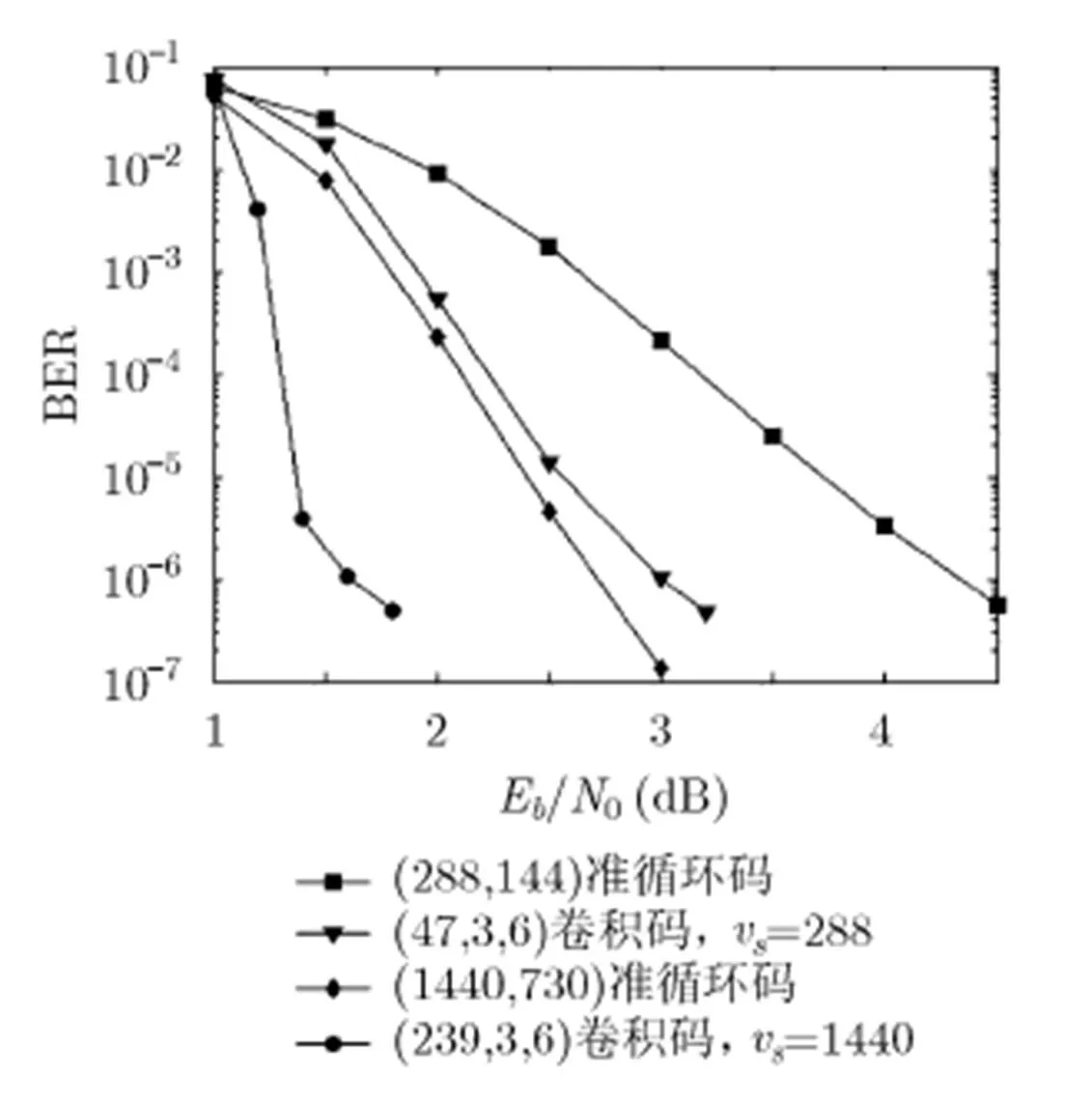
图2 QC-LDPC分组码与LDPC卷积码的BER性能
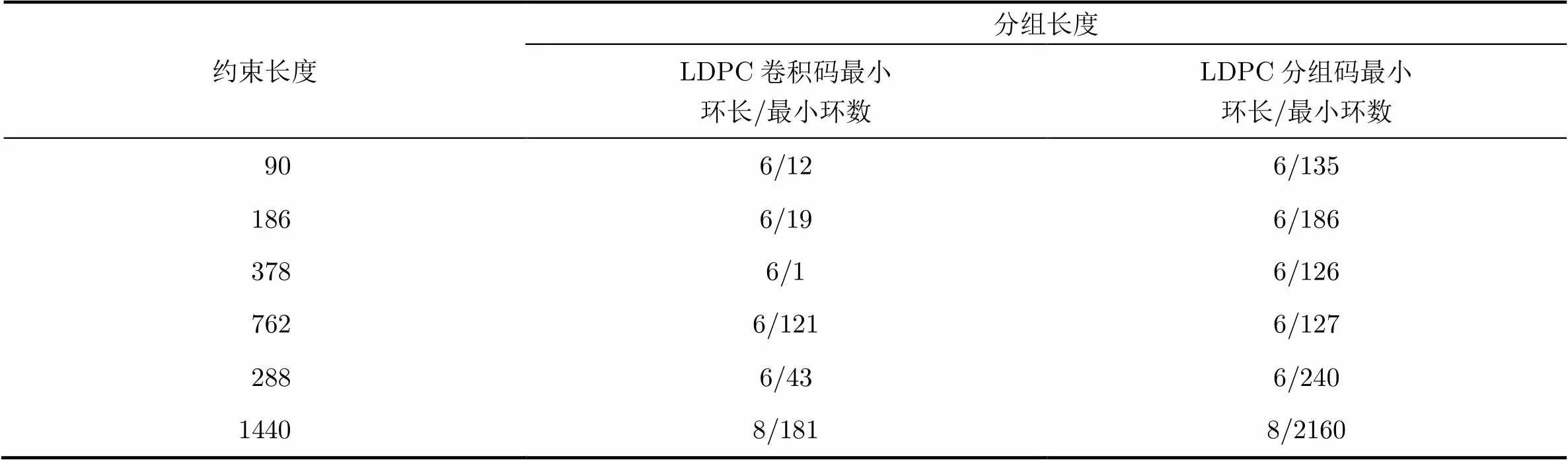
表1 码率3/6LDPC卷积码及其对应的QC-LDPC码环数
6 结束语
本文由QC-LDPC分组码获得LDPC卷积码的方法提出了用有限域上的元素构造时不变LDPC卷积码的新方法,并确保所获得的码具有快速编码特性、最大可达编码记忆以及设计码率。本文以码率为的MDS卷积码为例,给出了具体的构造方法及其仿真结果。在AWGN信道下的仿真结果表明,与具有类似结构的码相比,该构造方法所获得的LDPC卷积码在小的约束长度下就具有较低的误码平台和良好的译码性能。该码可用移位寄存器实现的快速编码算法以及可用滑动窗口译码器实现的BP译码算法使其适合于硬件实现。
[1] FELTSTROM A and ZIGANGIROV K. Time-varying periodic convolutional codes with low-density parity-check matrix[J]., 1999, 45(6): 2181-2191.
[2] BOCHAROVA I, KUDRYASHOV B, and JOHANNESSON R. Searching for binary and nonbinary block and
convolutional LDPC codes[J]., 2016, 62(1): 163-183.
[3] ZHAO Yue and LAU F. Implementation of decoders for LDPC block codes and LDPC convolutional codes based on GPUs[J]., 2015, 25(3): 663-672.
[4] ZHOU Hua and GOERTZ N. Recoverability of variable nodes in periodically punctured LDPC convolutional code[J]., 2015, 19(4): 521-524.
[5] BALDI M, CANCELLIERI G, and CHIARALUCE F. Array convolutional low-density parity-check codes[J]., 2014, 18(2): 336-339.
[6] GIOULEKAS F, PETROU C, VGENIS A,. On the construction of LDPC convolutional code ensembles based on permuted circulant unit matrices[C]. IEEE International Conference on Electronics, Circuits and Systems, Marseille, 2014: 407-410.
[7] JUNHO C and SCHMALEN L. Construction of protographs for large-girth structured LDPC convolutional codes[C]. IEEE International Conference on Communications, London, 2015: 4412-4417.
[8] SRIDHARAN A and COSTELLO D. A new construction for low density parity check convolutional codes[C]. Proceedings of the IEEE Information Theory Workshop, Bangalore, India, 2002: 212.
[9] ZHOU Hua and GOERTZ N. Girth analysis of polynomial- based time-invariant LDPC convolutional codes[C]. International Conference on Systems, Signals and Image Processing, Vienna, 2012: 104-108.
[10] TANNER R, SRIDHARA D, SRIDHARAN A,. LDPC block and convolutional codes based on circulant matrices[J]., 2004, 50(12): 2966-2984.
[11] ESMAEILI M and GHOLAMI M. Geometrically-structured maximum-girth LDPC block and convolutional codes[J]., 2009, 27(6): 831-845.
[12] PUSANE A, SMARANDACHE R, VONTOBEL P,. Deriving good LDPC convolutional codes from LDPC block codes[J]., 16(6): 897-900.
[13] MU Liwei, LIU Xingcheng, and LIANG Chulong. Construction of binary LDPC convolutional codes based on finite fields[J]., 2012, 16(6): 897-900.
[14] CHEN Chao, BAI Baoming, and WANG Xingmei. Construction of quasi-cyclic LDPC codes based on a two-dimensional MDS code[J]., 2010, 14(5): 447-449.
[15] JUSTESEN J. An algebraic construction of rate 1/convolutional codes[J]., 1975, 21(5): 577-580.
New Ensemble of Time-invariant LDPC Convolutional Codes with High Performance
MU Liwei①②LIU Xingcheng③ZHANG Han①②
①(School of Physics and Telecommunication Engineering, South China Normal University, Guangzhou 510006, China)②(Guangdong Provincial Key Laboratory of Quantum Engineering and Quantum Materials, South China Normal University,Guangzhou 510006, China)③(Department of Electronic and Communications Engineering, Sun Yat-sen University, Guangzhou 510006, China)
In this paper, a new ensemble of the polynomial matrix of a time-invariant LDPC convolutional code is proposed. Based on the method of deriving time-invariant LDPC convolutional codes from QC (Quasi-Cyclic)- LDPC block codes, the elements over finite fields are used to generate directly the polynomial parity-check matrices of LDPC convolutional codes. A concrete example of using MDS (Maximum-Distance Separable) convolutional codes to derive the polynomial matrices is given. The proposed method ensures the fast encoding property, maximum encoding memory and designed rate. Simulation results show that the proposed LDPC convolutional codes exhibit low error floor and good decoding performance under BP (Belief Propagation) decoding algorithm over AWGN (Additive White Gaussian Noise) channel.
LDPC convolutional codes; Finite fields; Fast encoding; Time-invariant; Maximum encoding memory
TN911.22
A
1009-5896(2016)09-2274-06
10.11999/JEIT151376
2015-12-08;
2016-05-06;
2016-07-04
国家自然科学基金(61401164, 61572534, 60141176, 61002012, 61501126),广东省自然科学基金(2014A030310308, S2013010016297),广东省优秀青年教师培养计划(YQ2015046)
The National Natural Science Foundation of China(61401164, 61572534, 60141176, 61002012, 61501126), The Natural Science Foundation of Guangdong Province of China (2014A030310308, S2013010016297), The High Education Excellent Young Teacher Program of Guangdong Province (YQ2015046)
穆丽伟 liweimu@m.scnu.edu.cn
穆丽伟: 女,1980年生,博士,讲师,研究方向为无线通信、信道编码.
刘星成: 男,1968年生,教授,博士生导师,研究方向为无线通信、信道编码.
张 涵: 男,1981年生,教授,硕士生导师,研究方向为信号处理、无线通信.

