基于知识的海杂波背景下距离扩展目标检测

许述文 薛 健 水鹏朗



基于知识的海杂波背景下距离扩展目标检测

许述文*薛 健 水鹏朗

(西安电子科技大学雷达信号处理国家重点实验室 西安 710071) (西安电子科技大学信息感知技术协同创新中心 西安 710071)

该文针对在辅助数据有限的情况下自适应检测器出现检测性能损失，提出基于杂波的先验知识分布的距离扩展目标自适应检测算法。复合高斯杂波的纹理和散斑的协方差矩阵分别被建模为服从逆伽玛分布的随机变量和逆复Wishart分布的随机矩阵。利用先验知识推导了纹理分量的最大后验估计，并结合广义似然比检验设计了不依赖辅助数据的距离扩展目标自适应检测器。仿真结果表明，提出的检测器在参数失配条件下具有好的鲁棒性，而且在辅助数据有限情况下检测性能优于传统的广义似然比检测器的检测性能。

距离扩展目标；先验知识；复合高斯杂波；逆伽玛分布；逆复Wishart分布

1 引言

随着宽带雷达的广泛应用，非高斯杂波背景下距离扩展目标的自适应检测获得了越来越多的关注[1,2]。宽带高分辨雷达(HRR)的分辨单元长度远小于目标的尺寸，因此观测目标会占据多个雷达距离单元，此时的目标称为分布式目标或者距离扩展目标。雷达目标检测中，认知杂波的特性是必不可少的并且可以改善检测方法的检测性能。目前，复合高斯模型被广泛地采用建模高分辨雷达下的非高斯杂波[1,3,4]。复合高斯模型采用两个独立的过程描述非高斯杂波：零均值复高斯过程的散斑分量和非负随机过程的纹理分量。文献[5]分析了杂波纹理分量的相干长度，分析结果表明纹理分量在一定的观测时间内可以看作是随机的常数。因此，复合高斯模型退化为了雷达目标检测中经常使用的球不变随机过程(SIRP)模型[6]。近年来，纹理分量为逆伽玛分布的广义Pareto功率分布被提出来建模高分辨雷达下的非高斯杂波[7,8]。文献[9]研究了实测杂波数据的幅度统计特性，研究结果表明逆伽玛纹理复合高斯模型可以很好地拟合实测的杂波。纹理分量先验分布的使用可以改善距离扩展目标检测器的检测性能。文献[1]根据3种广义似然比(GLRT)准则分别设计了3个逆伽玛纹理复合高斯杂波下距离扩展目标自适应检测器，仿真实验表明提出的检测器均优于传统广义似然比检测器。文献[10]分析了IPIX雷达采集的实测海杂波数据并表明相干雷达回波可以使用逆伽玛纹理复合高斯模型建模，同时也通过实测的海杂波数据评估了逆伽玛纹理下的线性门限广义似然比检测(LTGLRT)检测器和归一化自适应匹配滤波(NAMF)检测器。

许多自适应类的距离扩展目标检测器都需要使用足够的辅助数据估计真实的散斑协方差矩阵。然而有时辅助数据是有限的或者无法获得的，尤其是在非均匀杂波环境中[11]。辅助数据有限的情况下，需要估计协方差矩阵的自适应检测器的性能会出现严重损失，甚至无法检测。在这种情形下，可以使用杂波散斑分量的协方差矩阵的先验信息提高检测器的检测性能。文献[12,13]中分析了协方差矩阵的先验分布，表明可以使用逆复Wishart分布建模协方差矩阵。文献[14]考虑了逆伽玛纹理复合高斯非均匀杂波下点目标自适应检测，使用Gibbs抽样得到协方差矩阵的最小均方误差估计，设计的检测器在辅助数据较少的时候具有良好的检测性能，但是其具有较高的计算复杂度，而且仍然采用了辅助数据。文献[15]研究了MIMO雷达下K分布和广义Pareto功率杂波中的目标自适应检测，提出的检测器利用了主数据和辅助数据的散斑协方差矩阵均服从逆复Wisart分布的先验信息，仿真实验表明提出的检测器在辅助数据有限的情形下比一些已有的检测器检测性能好。逆伽玛纹理复合高斯杂波下的自适应距离扩展目标检测器在辅助数据有限情形下出现性能损失的问题尚未解决。鉴于此，本文将杂波的纹理分量建模为服从逆伽玛分布的随机变量，再将散斑分量的协方差矩阵的共轭先验分布建模为逆复Wishart分布。接着根据先验分布推导了纹理分量的最大后验估计，基于广义似然比设计了不依赖辅助数据估计协方差矩阵的自适应距离扩展目标检测器。最后通过仿真实验评估了检测器的检测性能，仿真结果表明，本文提出的检测器在辅助数据有限的情形下优于传统的广义似然比检测器，并且在参数失配情形下具有好的稳定性。

2 问题描述

2.1 假设检验描述

假设雷达发射个相干脉冲，待检测的目标占据个距离分辨单元。维复向量表示雷达回波中第个距离单元的回波数据。检测的目的是判决杂波背景中是否有距离扩展目标存在。因此该距离扩展目标检测问题可以转化为如式(1)的二元假设检验问题：

2.2 杂波模型

(4)

3 检测器设计

根据奈曼皮尔逊(NP)准则，最优的检测器可以通过似然比检验获得。然而，由于未知参数的存在，使得无法采用似然比检验推导出最优检测器。因此，在雷达目标检测中，通常采用广义似然比检验设计检测器。广义似然比检验可以描述检测问题为

(6)

(8)

(10)

将式(8)、式(9)、以及式(10)代入检验准则式(5)中，可得

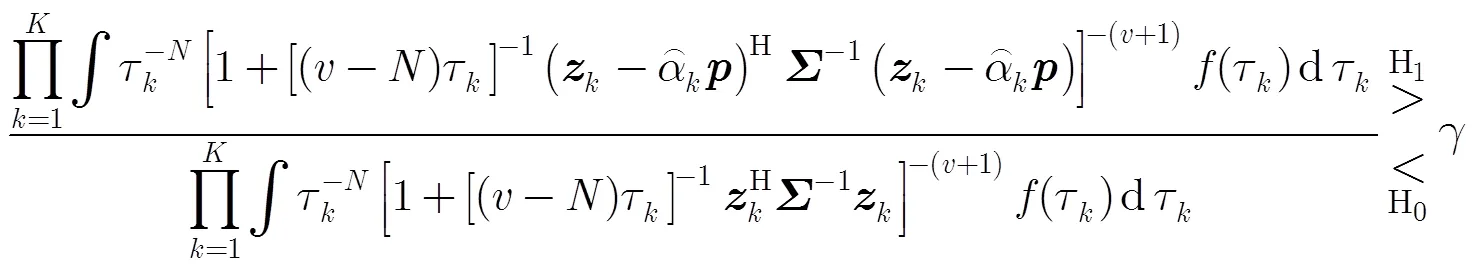
(12)

(13)

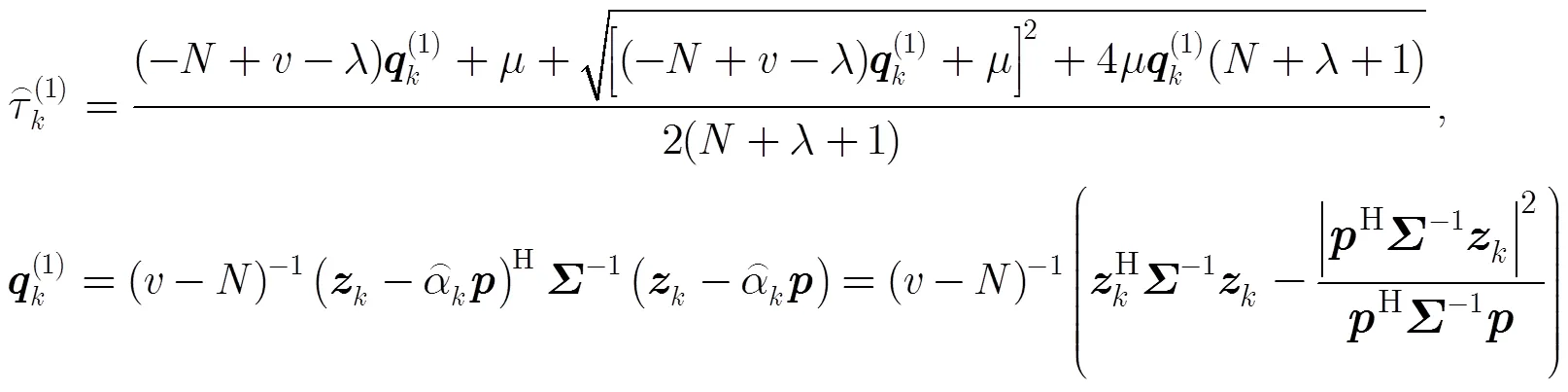
(15)

将式(14)和式(15)代入检验准则式(12)，经过整理得到检测器：

4 检测性能评估

4.1 仿真参数设置

本节采用蒙特卡洛仿真评估提出的检测器在逆伽玛纹理复合高斯杂波背景下距离扩展目标的检测性能。此外，将提出的检测器和传统的广义似然比(GLRT)检测器[17]进行检测性能比较。将提出的检测器记为BGLRT-IG检测器。

由于虚警概率的解析表达式无法获得，故采用纯杂波数据通过蒙特卡洛实验确定检测门限。虚警概率设置为，检测门限可以通过次独立的实验获得。试验中采用平均信杂比(A-SCR)，定义为[18]

4.2 目标模型的影响

本小节采用3种多主散射(MDS)模型评估检测器的检测性能。假设目标的总能量为1，表1列出了3种MDS模型。试验中，仿真参数设置为：脉冲数，距离扩展单元，逆复Wishart分布的自由度，逆伽玛纹理的形状参数，尺度参数，一阶迟滞相关系数。

表1 距离单元=8时3种MDS目标模型

距离单元编号12345678 目标模型M11/81/81/81/81/81/81/81/8 目标模型M21/41/41/41/40000 目标模型M310000000

图1显示了BGLRT-IG检测器在3种目标模型下的检测性能曲线。BGLRT-IG检测器在目标模型M1下的检测性能最优，从M1到M3模型，检测性能的损失逐渐增大。BGLRT-IG检测器是对每个距离单元处理过的能量进行累积，故在目标扩展程度匹配且能量分布均匀的时候，检测器的检测性能最优。随着目标扩展距离单元的失配，检测器对不包含目标能量的距离单元进行了累积，出现了坍塌损失，故而检测器的检测性能出现了损失。尤其是目标模型M3中，目标的能量集中到一个距离单元中。因此稀疏扩展目标的检测是将来需要解决的一个问题。

4.3 形状参数的影响

4.4 参数失配的影响

本小节讨论BGLRT-IG检测器在不同参数失配情形下的鲁棒性。生成数据时使用真实的参数，检测器中使用设定的参数。

图3仿真了形状参数失配情形下BGLRT-IG检测器的检测性能。仿真参数设置为：真实形状参数，设定的形状参数分别为,,,,,,,,。目标模型为M1模型。图3 中可以看出形状参数的失配几乎没有对检测器的检测性能造成损失。

图4仿真了一阶迟滞相关系数失配情形下BGLRT-IG检测器的检测性能。仿真参数设置为：真实一阶迟滞相关系数，设定的一阶迟滞相关系数分别为,,,,,,,。目标模型为M1模型。图4中显示一阶迟滞相关系数的失配对检测器的检测性能造成了轻微的损失，但在实际应用中这种损失可以忽略。图5仿真了自由度失配情形下BGLRT-IG检测器的检测性能。仿真参数设置为：真实自由度=12，设定的自由度分别为,,,,,,,,。目标模型为M1模型。图5中显示自由度的失配影响了检测器的检测性能，但影响是可以接受的。

总的来说，BGLRT-IG检测器在以上3个参数失配情况下具有稳定的检测性能。

4.5 仿真数据检测性能比较

本小节对逆伽玛纹理复合高斯杂波下BGLRT-IG检测器和传统的GLRT检测器的检测性能比较。仿真实验参数设置为：,,,,,, GLRT检测器的辅助数据单元个数分别为=8, 16和32。目标模型采用M1模型。

由图6可见，不依赖于辅助数据估计协方差矩阵的BGLRT-IG检测器的检测性能明显优于辅助数据分别为=8, 16和32时GLRT检测器的检测性能。由于GLRT检测器需要使用辅助数据估计的协方差矩阵代替真实的协方差矩阵，因此辅助数据的数量影响GLRT检测器的检测性能。随着辅助数据数量的越多，估计的协方差矩阵越接近真实的协方差矩阵，故GLRT检测器的检测性能越好。同样，辅助数据越少，检测器性能越差，甚至无辅助数据时导致其无法检测。BGLRT-IG检测器由于使用了协方差矩阵的先验信息，不需要估计协方差矩阵，所以在辅助数据有限情况下，BGLRT-IG检测器的检测性能好。

ROC曲线[19]通常也被用来评估检测器的检测性能。图7显示了A-SCR分别为-7 dB, -13 dB和-19 dB时BGLRT-IG检测器和GLRT检测器的ROC曲线。图7中曲线同样说明BGLRT-IG检测器优于辅助数据数量为32时GLRT检测器。因此，在数据有限条件下BGLRT-IG检测器比传统的检测器检测性能好。

4.6 实测数据检测性能比较

本小节使用南非的实测数据比较BGLRT-IG检测器和GLRT检测器的检测性能。南非数据采集于2006年，是南非Fynmeet海杂波测量实验的一部分[20]。本文采用数据集TFC15_005作为实测海杂波数据。

图8显示了实测海杂波下BGLRT-IG检测器和GLRT检测器的检测性能。实验参数设置为：,,=12和16。目标占据4个距离单元，并且目标模型采用M1模型。仿真的目标添加在实测海杂波数据的第25至28距离单元中。图8中曲线显示，实测海杂波数据中在辅助数据有限情形下，BGLRT-IG检测器的检测性能优于GLRT检测器。

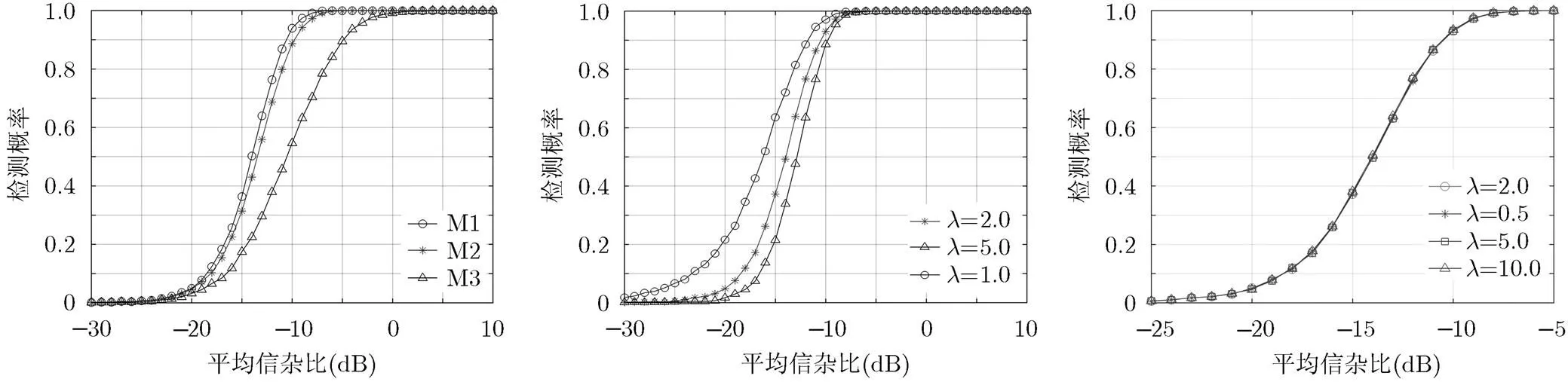
图1 目标模型M1, M2, M3下BGLRT-IG   图2 不同形状参数下BGLRT-IG    图3 形状参数失配下BGLRT-IG

检测器的检测性能曲线      检测器的检测性能曲线      检测器的检测性能曲线

图4 一阶迟滞相关系数失配下BGLRT   图5 自由度失配下BGLRT-IG   图6 仿真数据下BGLRT-IG检测器

-IG检测器的检测性能曲线      检测器的检测性能曲线      和GLRT检测器检测性能比较

图7 BGLRT-IG检测器和GLRT       图8 实测数据下BGLRT-IG检测器

检测器的ROC曲线          和GLRT检测器检测性能比较

5 结束语

为解决辅助数据有限情况下时复合高斯杂波下距离扩展目标的自适应检测问题，本文提出了基于杂波先验知识的BGLRT-IG检测器。杂波的纹理分量被建模为服从逆伽玛分布的随机变量，杂波散斑分量的协方差矩阵被建模为服从逆复Wishart分布的随机矩阵。然后基于先验知识和广义似然比检验准则设计了BGLRT-IG检测器。仿真实验表明，在形状参数、一阶迟滞相关系数和自由度失配时，本文提出的检测器具有良好的鲁棒性；在仿真数据和实测数据中，当辅助数据有限时，BGLRT-IG检测器优于传统的GLRT检测器，检测性能更优。

参考文献

[1] SHANG Xiuqin, SONG Hongjun, WANG Yu,Adaptive detection of distributed targets in compound-Gaussian clutter with inverse Gamma texture[J]., 2012, 22(6): 1024-1030. doi: 10.1016/j.dsp.2012. 05.002.

[2] YANG Xiaoliang, WEN Gongjian, MA Conghui,CFAR detection of moving range-spread target in white Gaussian noise using waveform contrast[J]., 2016, 13(2): 282-286. doi: 10.1109/ LGRS.2015.2511060.

[3] KEITH I, ORELANDE M R, SUVOROVA S,Parametric texture estimation and prediction using measured sea clutter data[J].,&, 2016, 10(3): 449-458. doi: 10.1049/iet-rsn.2015.0098.

[4] SANGSTON K J, GINI F, and GRECO M S. Adaptive detection of radar targets in compound-Gaussian clutter[C]. 2015 IEEE Radar Conference (RadarCon), Johannesburg, South Africa, 2015: 0587-0592. doi: 10.1109/RADAR.2015. 7131066.

[5] CONTE E, BISCEGLIE M D, GALDI C,A procedure for measuring the coherence length of the sea texture[J]., 1997, 46(4): 836-841. doi: 10.1109/19.650784.

[6] YI Lei, YAN Liang, and HAN Ning. Simulation of inverse Gaussian compound Gaussian distribution sea clutter based on SIRP[C]. Advanced Research and Technology in Industry Applications (WARTIA) of IEEE Workshop, 2014: 1026-1029. doi: 10.1109/WARTIA.2014.6976451.

[7] ROSENBERG L and BOCQUET S. Application of the Pareto plus noise distribution to medium grazing angle sea- clutter[J]., 2015, 8(1): 255-261. doi: 10.1109/JSTARS.2014.2347957.

[8] BOCQUET S, ROSENBERG L, and WATTS S. Simulation of coherent sea clutter with inverse Gamma texture[C]. 2014 International Radar Conference, Lille, France, 2014: 1-6. doi: 10.1109/RADAR.2014.7060347.

[9] BALLERI A, NEHORAI A, and WANG J. Maximum likelihood estimation for compound-Gaussian clutter with inverse gamma texture[J]., 2007, 43(2): 775-779. doi: 10.1109/ TAES.2007.4285370.

[10] STINCO P, GRECO M, and GINI F. Adaptive detection in compound-Gaussian clutter with inverse-gamma texture[C]. Proceedings of 2011 IEEE CIE International Conference on Radar, Chengdu, China, 2011: 434-437. doi: 10.1109/CIE- Radar.2011.6159570.

[11] RICHMOND C D. Performance of a class of adaptive detection algorithms in nonhomogeneous environments[J]., 2000, 48(5): 1248-1262.doi: 10.1109/78.839973.

[12] SVENSSON L and LUNDBERG M. Analytical expression for the posterior distribution of signals in colored Gaussian noise[C]. Conference Record of the Thirty-Sixth Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 2002: 1767-1771. doi: 10.1109/ACSSC.2002. 1197078.

[13] SVENSSON L and LUNDBERG M. On posterior distributions for signals in Gaussian noise with unknown covariance matrix[J]., 2005, 53(9): 3554-3571. doi: 10.1109/TSP.2005. 853102. doi: 10.1109/TSP.2005.853102.

[14] 谢洪森, 邹鲲. 一种非均匀场景复合高斯杂波下的自适应检测器[J]. 电子与信息学报, 2011, 33(10): 2433-2437. doi: 10.3724/SP.J.1146.2010.01412.

XIE Hongsen and ZOU Kun. Adaptive detector in compound Gaussian clutter of nonhomogenous environments[J].&, 2011, 33(10): 2433-2437. doi: 10.3724/SP.J.1146.2010.01412.

[15] KONG Lingjiang, LI Na, CUI Guolong,Adaptive Bayesian detection for multiple-input multiple-output radar in compound-Gaussian clutter with random texture[J].,&, 2016, 10(4): 689-698. doi: 10.1049/iet-rsn.2015.0241.

[16] LI Na, CUI Guolong, YANG Haining,Knowledge-aided Bayesian detection with MIMO radar in compound-Gaussian clutter[C]. IET International Radar Conference, Hangzhou, 2015: 1-6. doi: 10.1049/cp.2015.1118.

[17] SHUAI X F, KONG L J, and YANG J Y. Performance analysis of GLRT-based adaptive detector for distributed targets in compound-Gaussian clutter[J]., 2010, 90(1): 16-23. doi: 10.1016/j.sigpro.2009.05.008.

[18] XU Shuwen, Shui Penglang, and CAO Yunhe. Adaptive range-spread maneuvering target detection in compound- Gaussian clutter[J]., 2015, 36(1): 46-56. doi: 10.1016/j.dsp.2014.09.010.

[19] BENEDETTO A, BENEDETTO F, DE BLASIIC M R,Reliability of signal processing technique for pavement damages detection and classification using ground penetrating radar[J]., 2005, 5(3): 471-480. doi: 10.1109/JSEN.2005.846176.

[20] HERSELMAN P L and BAKER C J. Analysis of calibrated sea clutter and boat reflectivity data at C- and X-band in South African coastal waters[C]. IET International Conference on Radar Systems, Edinburgh, UK, 2007: 1-5. doi: 10.1049/cp:20070616.

许述文： 男，1985年生，副教授，研究方向为雷达目标检测、时频分析.

薛 健： 男，1993年生，硕士生，研究方向为宽带雷达距离扩展目标检测.

水鹏朗： 男，1967年生，教授，研究方向为雷达信号处理和图像处理.

Adaptive Detection of Range-spread Targets Based on Knowledge in Sea Clutter Background

XU Shuwen XUE Jian SHUI Penglang

(,,’710071,) (,’710071,)

For the problem of detection performance loss of adaptive detectors on the condition that the secondary data are limited, the adaptive detection method of range-spread target based on the prior knowledge of clutter is proposed. The texture and the covariance matrix of speckle of clutter are respectively modeled as the random variable which follows the inverse Gamma distribution and the random matrix which follows the inverse complex Wishart distribution. Based on the prior knowledge, the Maximum(MAP) estimation of texture component is obtained and the adaptive detector of range spread target which does not need the secondary data is designed via utilizing the generalized likelihood ratio test. Finally, the detection performances of the proposed detector are evaluated and the experimental results illustrate that the proposed detector is robust in parameters mismatched situation and outperforms the conventional generalized likelihood ratio test detector for range-spread target in limited secondary data scenarios.

Range-spread target; Prior knowledge; Compound Gaussian clutter; Inverse Gamma distribution; Inverse complex Wishart distribution

TN957.51

A

1009-5896(2016)12-3004-07

10.11999/JEIT160905

2016-09-07；改回日期：2016-11-09；

2016-12-02

许述文 swxu@mail.xidian.edu.cn

国家自然科学基金(61201296, 61372136)，中央高校基本科研业务费(JB160224)，陕西省科协青年人才托举计划(20160205)

The National Natural Science Foundation of China (61201296, 61372136), The Fundamental Research Funds for the Central Universities (JB160224), Young Talent Fund of University Association for Science and Technology in Shaanxi Province (20160205)