一种多路并行盲搜索的空时二维抗干扰算法
秦明峰,惠沈盈,范广伟
一种多路并行盲搜索的空时二维抗干扰算法
秦明峰1,2,惠沈盈1,2,范广伟1,2
(1.卫星导航系统与装备技术国家重点实验室,河北石家庄050081;2.河北省卫星导航技术与装备工程技术研究中心,河北石家庄050081)
针对卫星导航抗干扰中传统的空时自适应处理算法运算量大、处理速度较慢的问题,在介绍多级维纳滤波基本原理的基础上,提出了一种多路并行的盲搜索空时二维抗干扰自适应处理算法。该方法采用多级维纳滤波降维处理的方法求解信号子空间和干扰子空间,从而使输出信号的信干噪比达到最优,实现干扰的有效抑制。仿真结果表明,该算法具有较好的抗干扰性能,且运算量较低,有较好的工程应用前景。
空时自适应;多级维纳滤波;盲搜索;干扰抑制
引用格式:秦明峰,惠沈盈,范广伟.一种多路并行盲搜索的空时二维抗干扰算法[J].无线电工程,2016,46(5):29-32.
0 引言
随着卫星导航系统在民用和军事等领域中的广泛应用,其易于受到干扰的问题日益显现出来[1]。为了保证卫星导航接收机在复杂的电磁干扰环境下能提供有效的导航服务,必须研究适用于卫星导航系统的干扰抑制技术[2-3]。多级维纳滤波[4-6]是一种快速的维纳滤波算法,不需矩阵求逆,计算量低,在空时二维自适应处理中具有较好的应用前景,如通信干扰抑制中的应用[7-8],在导航接收机干扰抑制中的应用[9-10]。
本文研究了基于盲搜索的线性约束空时自适应处理算法,结合多路数字信号处理技术,既能够有效抑制快变干扰,又能够在感兴趣的卫星方向上形成多路波束,实现干扰场景下卫星信号的有效接收。
1 空时二维自适应处理
在卫星导航系统中,干扰的功率、形式及个数来波方向都无法做到事先预知,因此采用空时二维的自适应滤波器,可在不知道干扰数目及形式的条件下实现干扰信号的有效抑制。空时二维处理器由M个阵元组成,阵元2~M对应通道后的FIR滤波器阶数为N,W=[1,w21,w22,…,w2N,…,wM1,w22,…,wMN]T为加权系数,每个节拍延时为τ。功率倒置空时自适应处理[11-14]阵列结构如图1所示。
功率倒置的空时自适应处理的空时二维抗干扰处理算法通常在保证输出总功率最小的条件下,使期望信号s的增益尽可能为常数。自适应地在各个干扰方向产生相应的零陷,即零陷的深度随干扰功率的增强而加深。由于导航卫星的发射功率限制,导航信号到达地面时已经非常微弱,通常在噪底以下20~30 dB左右,因此算法翻转后不会对导航信号的接收造成影响;并且算法通过产生的零陷实现对干扰信号的抵消,相对地提高了接收机的输出信干噪比。根据最小均方准则,功率倒置算法实质上是一种使输出信干噪比最大的算法。

图1 功率倒置空时自适应处理阵列结构
但是如果不加约束,算法输出 Pout最小值在W=0时取得,得到的结果没有实际工程意义,因此需要在考虑实际工程应用的条件下,增加合适的约束条件,工程应用中常采用滤波器对期望信号为常数的约束方法,即WHs=常数,s为期望信号矢量。从而最优化准则成为:
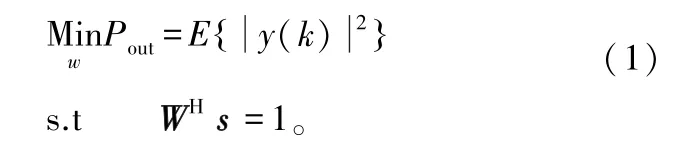
功率倒置算法实质上是一种具有严格约束条件的自适应算法,其约束条件为WHs=1。如果直接把期望信号的导向矢量设为s=[1,0,0…,0]T,则权矢量为,即把阵元1上的信号作为参考信号,通过选择加权矢量使阵元2~M加权输出与期望信号之间误差信号的均方值最小。
2 算法描述
功率倒置的算法虽然有较好的干扰抑制性能,但是本身结构较为复杂,在复杂电磁环境下,受到闪烁干扰和突发干扰等的影响,干扰抑制的性能较差,且运算量较高,不利于实时实现。为了降低算法运算量,本文采用一种基于多级维纳滤波的空时二维盲搜索算法来求解信号子空间和干扰子空间,从而实现干扰的有效抑制。
多级维纳滤波空时二维处理算法是利用信号子空间和干扰子空间的正交行对输入数据进行多次正交投影分解[15],依次正交分解可得到2个正交的子空间,一个与期望信号平行,另一个垂直于这个子空间,逐次分解下去,可构造空时二维抗干扰滤波器。
从公式推导中可以看出,张成的子空间满足:

AJ零空间的正交基矢量的求解可采用QR分解实现。AJ=QU,其中列正交矩阵Q为MN×MN维,上三角矩阵U为MN×D维,由于AJ是一个列满秩矩阵,设矩阵Q的列矢量表示为,那么,
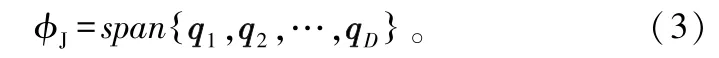
正交矩阵Q的后MN-D个列矢量张成的子空间与前D个矢量所张成的子空间相互正交,因此这MN-D个正交矢量可以作为AJ的正交基矢量,其形式可用下式表示:

通过式(4)求得MN-D个基矢量后,可继续求解空时二维权矢量W(MN×1维),,即对正交基进行线性组合,可得:

在实际应用中,为了增强期望信号的能量,通常是在卫星信号的波达方向上增加约束,则需要使得,也就是,其中θ0为卫星信号的来向,fc为卫星信号的载频。系数矩阵H为列满秩的超定方程,所以矢量d可以用最小二乘法求得:
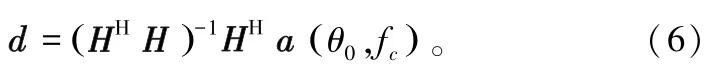
代入式(5),可以得到权矢量的表达式为:

假定卫星信号来向的搜索范围θ∈[θ1θ2],设定搜索步进为Δθ,基于多级维纳滤波的空时二维盲搜索算法的实现步骤如下:
迭代初始化:
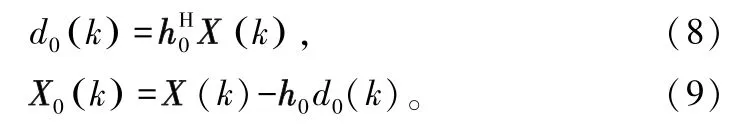
多级维纳滤波前向迭代过程,由以下几个公式构成:

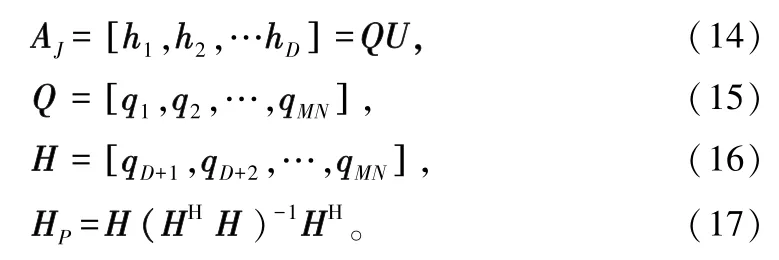
则滤波器的最优权系数描述为:
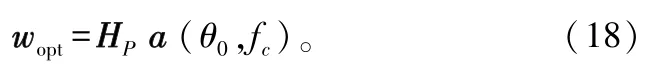
本文提出算法每搜索一个角度,仅需要做MN次乘法,相比2次矩阵求逆的运算量O((MN)4-2(MN)3+2(MN)2-1),远不在一个数量级,很容易在硬件平台上实现。
3 仿真结果分析
为了验证本文提出的一种多路并行盲搜索的空时二维抗干扰算法的性能,设定如下仿真,并验证提出算法的性能。
天线阵采用4阵元均匀线阵,延时抽头数为4。卫星信号波达方向是0°,输入信噪比为-30 dB;宽带干扰方向为(120°,30°)和(300°,50°),带宽为20 MHz,输入干信比为60 dB。实验中比较了功率倒置空时处理算法和传统LCMV算法,空时抗干扰算法以及本文提出算法的性能。
仿真中天线采用4阵元均匀圆阵,时域上采用4阶时延,假设卫星信号的波达方向为俯仰方位(0°,0°)方向,信噪比为-30 dB,存在2个带宽为20 MHz的宽带干扰,方向为(120°,30°)和(300°,50°),实验中采用功率倒置算法、传统的LCMV算法与本文提出的算法进行对比,仿真结果如图2、图3和图4所示。
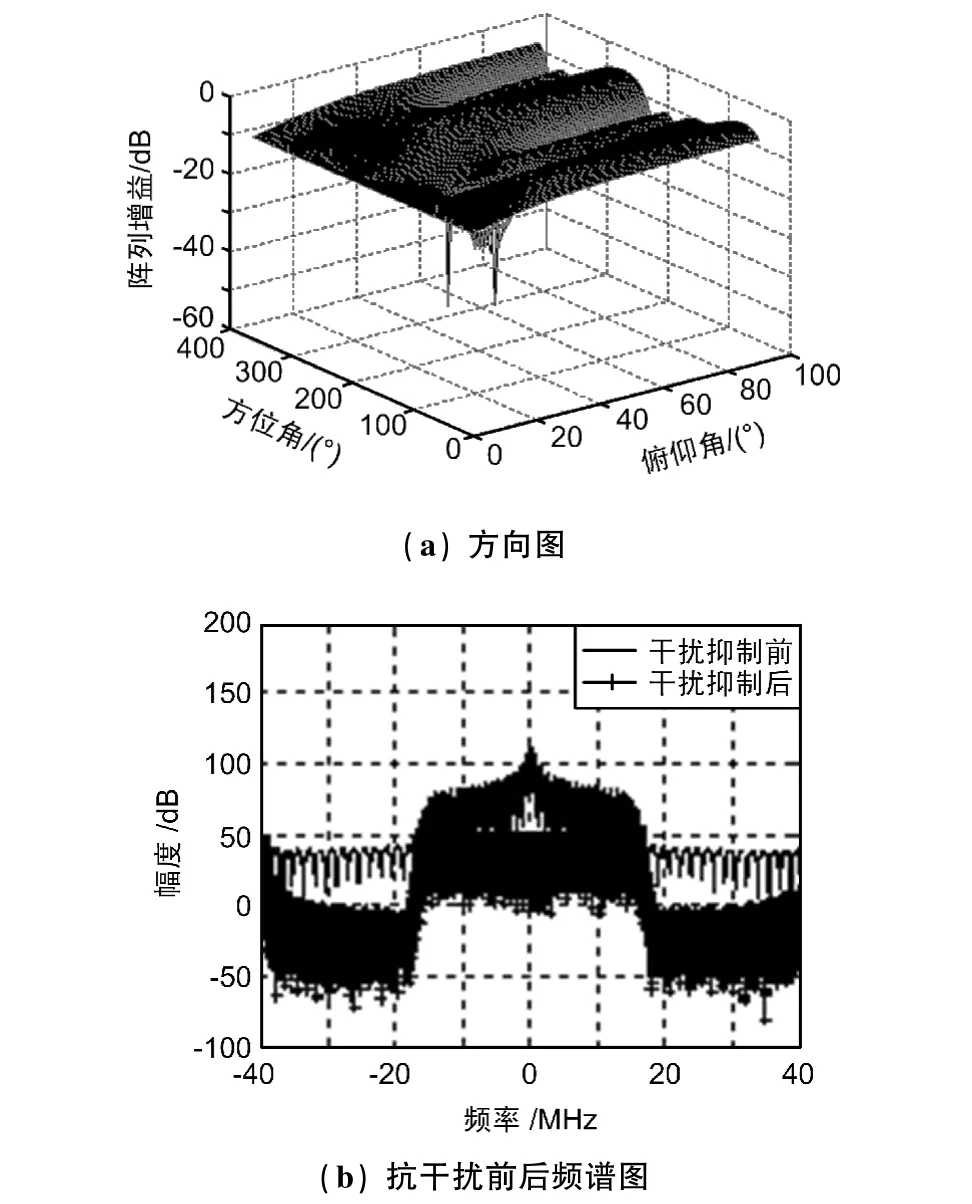
图2 功率倒置法的方向图及侧视图

图3 传统LCMV算法的方向图及侧视图
由图2、图3和图4可以看出,3种算法在干扰方向均产生较深的零陷,但是比较抗干扰前后的频谱图可以看出,本文提出算法抗干扰后的频谱图最为平滑,对信号的影响最小。
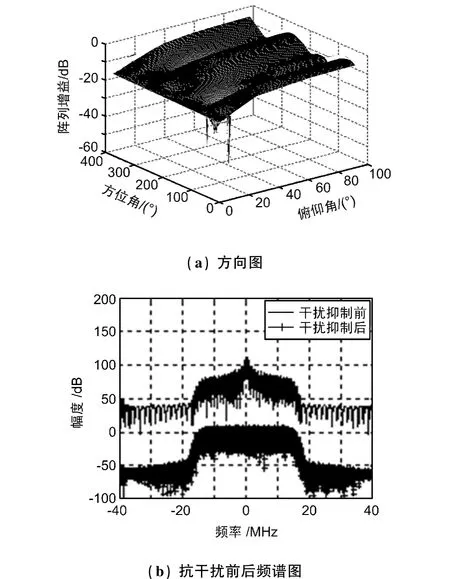
图4 本文算法的方向图及侧视图
3种算法抑制干扰后的性能参数如表1所示。从表1中可以看出,本文算法输出SINR明显高于功率倒置算法,其中本文算法相比功率倒置算法输出SINR接近改善了6 dB。相比传统LCMV空时抗干扰算法,本文算法性能仅仅恶化了约0.19 dB,但却换来了运算量的大大降低。
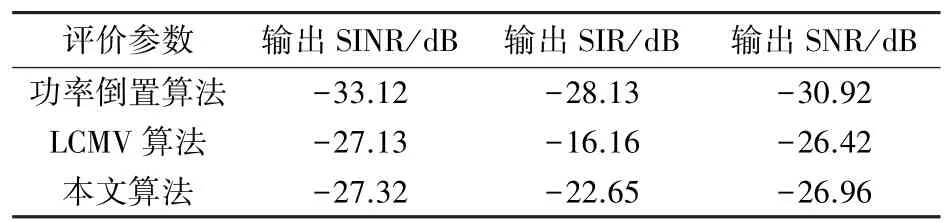
表1 滤波性能比较
4 结束语
本文根据GNSS接收机的特点,在约束均方误差最小准则下,提出了一种应用于GNSS接收机的盲搜索的多级维纳滤波自适应空时二维干扰抑制算法。经过仿真分析可以发现,该算法对干扰具有较好的抑制效果,输出信噪比相比功率倒置空时抗干扰算法要高,对卫星信号影响较小,且运算量较小,有利于在高动态接收机中实现。
[1] 项建弘,郭黎利,陈立明.GPS空时自适应抗干扰系统性能研究[J].系统工程与电子技术,2009,31(5):1 022-1 025.
[2] 王 和,刘光斌,程俊仁,等.卫星导航接收机抗干扰测试评估方法研究[J].无线电工程,2014,44(3):5-7.
[3] 张晓明,王莎莎.针对窄带干扰抑制的数字陷波器设计[J].无线电工程,2008,38(5):24-25.
[4] 杨 亮.通信系统中空时二维抗干扰方法研究[J].无线电通信技术,2013,39(6):74-77.
[5] GOLDSTEIN J S,REED I S,SCHARF L L.A Multistage Representation of the Wiener Filter Based on Orthogonal Projections[J].IEEE Trans on Information Theory,1998,44(7):2 943-2 959.
[6] SCHMIDT R O.Signal Subspace Approach to Multiple E-mitter Location Spectral Estimation[D].CA:Stanford Univ,1981.
[7] OHAM M,SUN Y,ZOLTOWSKI M D,et al.A New Backward Recursion for the Multistage Nested Wiener Filter Employing Krylov Subspace Methods[C]∥IEEE Military Communications Conference,2001:1 210-1 213.
[8] WERNERStefan,WITH Matias.Householder Multistage WienerFilterforSpaceTimeNavigationReceivers [J].IEEE Transactions on Aerospace and Electronic Systems,2007,43(3):975-988.
[9] 狄旻珉,张尔扬.一种多级 GPS抗干扰接收机设计[J].通信学报,2005,26(11):82-86.
[10]DELAMARERC,SAMPAIO-NETOR.Space-time Adaptive Reduced-rank Processor for Interference Mitigation in OS-COMA Systems[J].LET Communications,2008,2(2):388-397.
[11]司东晓,蔚保国.GPS接收机空时二维抗干扰技术研究[J].无线电工程,2010,40(3):33-35.
[12]刘 荣,王立平,陈杨.GPS接收机抗干扰性能仿真研究[J].无线电通信技术,2014,40(1):58-60,64.
[13]郭 艺.GPS空时抗干扰理论与实现关键技术研究[D].长沙:国防科技大学,2007.
[14]王永良,彭应宁.空时自适应信号处理[M].北京:清华大学出版社,2000.
[15]SADY.Iterative Methods for Sparse Linear Systems[M]. USA:SocietyforIndustrialandAppliedMathematic,1996.
A Space-time Anti-interference Algorithm of Multi-channel Parallel Blind Search
QIN Ming-feng1,2,HUI Shen-ying1,2,FAN Guang-wei1,2
(1.State Key Laboratory of Satellite Navigation System and Equipment Technology,Shijiazhuang Hebei 050081,China;2.Hebei Satellite Navigation Technology and Equipment Engineer Technology Center,Shijiazhuang Hebei 050081,China)
In satellite navigation anti-interference,the traditional space-time adaptation processing algorithm has such defects as heavy computation and low processing speed.Based on analyzing the principle of multi-stage wiener filtering,this paper puts forward a space-time two-dimensional adaptive processing algorithm of multi-channel parallel blind search.This algorithm uses the dimension reducing processing of multi-stage Wiener filter to solve the interference subspace and signal subspace so as to make the output SINR optimal and realize effective interference suppression.The simulation results show that this algorithm has better anti-interference performance,with low computation and a good application prospects.
space-time adaptation;multistage Wiener filtering;blind search;interference suppression
TN911.23
A
1003-3106(2016)05-0029-04
10.3969/j.issn.1003-3106.2016.05.08
2016-01-20
国家高技术研究发展计划(“863”计划)基金资助项目(2012AA121801)。
秦明峰 男,(1975—),硕士,高级工程师。主要研究方向:卫星导航接收终端设计。
范广伟 男,(1982—),博士,工程师。主要研究方向:卫星导航抗干扰、干扰监测。

