基于小波变换和改进萤火虫算法优化LSSVM的短期风速预测

方必武，刘涤尘，王 波，闫秉科，汪勋婷



基于小波变换和改进萤火虫算法优化LSSVM的短期风速预测

方必武，刘涤尘，王 波，闫秉科，汪勋婷

(武汉大学电气工程学院，湖北 武汉 430072)

准确预测风速对风电规模化并网至关重要。为提高短期风速预测精度，提出一种基于小波分解和改进的萤火虫算法优化最小二乘支持向量机超参数的风速预测模型。首先利用小波变换将风速时序分解为近似序列和细节序列，然后对各序列分别利用一种新颖的混沌萤火虫算法优化LSSVM进行预测，最后将各序列预测值叠加得到最终风速预测值。在两种时间尺度的实测数据上进行仿真计算。结果表明，该算法较交叉验证的LSSVM, IPSO-LSSVM, WD-DE-LSSVM及BP神经网络等多种经典算法预测精度更高，表明了该算法的有效性和优越性。

短期风速预测；小波分解与重构；混沌萤火虫算法；最小二乘支持向量机

0 引言

随着化石能源的日渐枯竭以及环境污染的日益严重，风电作为一种清洁可再生能源发电形式得到了世界各国的广泛重视。风电大规模并网后，可能会出现电压和频率偏差、电压波动甚至脱网等现象，在我国多个区域电网还存在风电上网后的系统调峰难题，这些问题产生的根源是风速的波动性和随机性导致风电出力呈现出间歇性和不确定性的特点。因此，对风电场短期风速进行准确预测至关重要[1-2]。

目前，国内外学者针对风速预测已进行了一些研究，主要可分为基于物理模型和基于历史数据预测两类方法[3]。物理模型法采用天气预报数据进行预测，但是由于我国数值气象模型难获取且气象预报数据更新频率低，仅适用于中长期风速预测[4]。基于历史数据预测的方法较多，主要有时间序列法[5]、空间相关法[6]、高斯过程回归[7]、神经网络[8]、支持向量机[9]、最小二乘支持向量机[10]等方法。其中最小二乘支持向量机(Least Squares support vector machines, LSSVM)因其训练时间短、泛化能力强、精度高等优点而得到了广泛的应用[11]。然而，由于风速的高度随机性和影响因素的复杂性，目前上述预测方法绝对平均误差为25%～40%，还未达到一定的满意程度[3]。

最小二乘支持向量机的预测效果与其模型超参数紧密相关，已有学者研究利用遗传算法、粒子群算法和改进的粒子群算法等智能仿生算法对LSSVM进行参数寻优[12-15]。研究结果表明参数寻优可以提高风速预测的精度，而且寻优算法的全局寻优能力越好则模型预测精度越高。可见，使用性能更好的智能寻优算法对最小二乘支持向量机的参数进行优化，是一种提高风速预测精度的有效方法。

基于此，本文使用一种新颖的智能优化算法—萤火虫算法(Firefly algorithm, FA)—对LSSVM进行参数寻优。在进行预测前，利用小波分解技术将原始风速数据分解为近似序列和细节序列，充分利用时序数据不同频率上的规律性。在基本萤火虫算法的基础上进行改进，引入自适应惯性权重(Adaptive inertia weight)，提高算法的收敛速度，同时引入混沌(Chaos)机制，解决算法的早熟问题，增强算法的全局寻优能力。在10分钟级和小时级两种尺度的实测数据上进行算例验证，结果表明本文提出的算法模型较多种现行的经典算法具有更高的预测精度和稳定性。

1  小波分解与重构

将实测风速序列视为时序信号，为更好地观察信号的细节并去除噪声，通常需要进行信号变换，小波分解(Wavelet decomposition, WD)是一种应用较多的手段[16-17]。其基本原理是根据Mallat 提出的多分辨率思想[18]，将非平稳的离散风速序列分解为不同频率的高频细节序列和一个低频近似序，为最大分解层数。通常采用db3小波基进行3层分解。其分解过程为

针对重构后的细节序列和近似序列分别进行预测，可以充分利用分解重构对信号特征的挖掘，从而减小预测误差。

2  最小二乘支持向量机回归模型

基于基本支持向量机改进的最小二乘支持向量机(LSSVM)，采用最小二乘线性系统作为损失函数，用等式约束代替支持向量机(Support Vector Machines, SVM)中的不等式约束条件，将二次规划问题求解转化为线性方程组求解，简化了计算的复杂性，提高了算法的收敛速度，被广泛应用于预测领域[19]。其基本原理如下[20-21]：

相应的拉格朗日函数为式(7)。

最终得到回归函数：

3  基于WD和改进萤火虫算法优化LSSVM的风速预测模型

3.1 基于改进萤火虫算法的LSSVM参数优化

3.1.1基本萤火虫算法原理

萤火虫算法(Firefly Algorithm, FA)是剑桥大学Dr. YANG 在2008年提出的一种新颖的生物群智能随机优化算法[23]。通过模拟萤火虫因觅食、择偶等习性而产生的相互因光吸引而移动的行为来解决最优问题。在算法中，每个萤火虫看作是搜索空间中的一个有位置没有体积的微粒，每个位置代表一个解，通过周围个体同伴所发荧光亮度和光强吸收系数决定移动的距离，不断在搜索空间进行搜索，最终找到最优解。基本萤火虫算法具有原理简单、参数少、易于实现、较强的全局寻优能力和收敛能力等特点，有学者使用14个著名的优化问题进行试验，结果绝大部分结果表现比PSO更为出色[24]。

萤火虫算法数学描述如下：

亮度和吸引度是萤火虫优化算法中的两个主要因素，分别定义如下。

3.1.2改进1-惯性权重

与其他进化算法相似，萤火虫算法在迭代后期存在容易在局部或全局极值附近反复振荡的问题。由(15)可知这是因为随着萤火虫距离的减小，彼此间的相对吸引度增大，导致移动距离过大而无法稳定到极值位置。为解决此问题，借鉴粒子群算法中的惯性权重改进策略[25-26]，使用如式(17)线性递减惯性权重对基本萤火虫算法进行改进。

3.1.3改进2-混沌机制

为进一步提高算法的寻优精度，考虑利用混沌运动的遍历性、随机性等特点，在惯性权重萤火虫算法的基础上，引入混沌思想，从而提高萤火虫种群的多样性和寻优的遍历性，增加算法跳出局部极值点的能力。

混沌优化基本思想是将优化变量通过混沌映射规则映射到混沌变量空间的取值区间内，利用混沌变量的遍历性和随机性寻优搜索，最后将获得的优化解线性转化到优化空间[27]。

产生混沌序列的方法有很多，目前应用最为成熟的是Logistic映射，本文即采用此方法，其数学表达式为

在得到混沌序列之后，用式(20)进行载波操作，映射到优化空间范围。

萤火虫的混沌优化过程为：在每一代优化过程中，选取表现最好的个萤火虫作为精英个体进行混沌优化，按设定的混沌搜索代数由式(19)产生混沌序列，然后按照式(20)将混沌序列映射回萤火虫搜索空间，最后对精英个体进行混沌搜索，若搜索到更优个体则予以替换。

3.1.4 CFA优化LSSVM参数流程

3) 按照式(14)计算萤火虫之间的欧式距离，按式(15)计算萤火虫之间的吸引度。

4) 按式(17)计算惯性权重，比较萤火虫之间的亮度，亮度较小的吸引亮度较大个体，按照式(18)更新萤火虫位置。

5) 重新计算萤火虫的适应度，取前个精英个体进行式(19)、式(20)的混沌操作并进行遍历搜索，若搜索到更优位置，则更新精英个体，否则直接转下一步。

3.2 WD-CFA-LSSVM风速预测

3.2.1原始数据预处理

从气象部门或风电场获取原始按10分钟级和 小时级两种尺度采集的时序风速数据，对数据进行归一化处理。归一化处理可以减小不健康数据对预测效果的影响，加快模型样本的训练速度和收敛速度。本文采用经典的线性归一化函方法，如式(22)所示。

3.2.2训练样本构造

3.2.3 WD-CFA-LSSVM风速预测框架

至此可得到本文提出的WD-CFA-LSSVM的风速预测模型如图1。

图1 WD-CFA-LSSVM风速预测流程

4  算例分析

4.1 数据准备

为验证本文算法的有效性，取10分钟级和小时级两种时间尺度的实测风速数据进行仿真计算。10分钟级数据为1天的每10 min的实测数据，对最后4小时的24个点进行提前10 min预测，小时级取6天的数据对最后1天的24个点进行提前1 h预测。原始风速如图2所示。

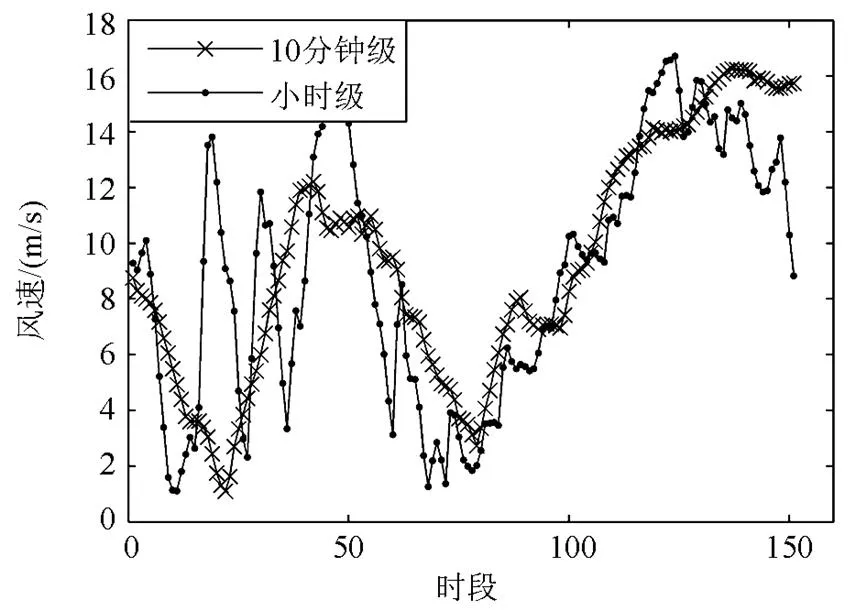
图2原始实测风速数据

4.2 算法设置说明

目前利用粒子群或微分进化算法进行LSSVM优化的研究已证明可在一定程度提升预测精度，因此将本文模型与目前预测效果较好的IPSO-LSSVM，WD-DE-LSSVM模型以及经典的BP神经网络模型进行仿真结果对比。IPSO及DE的参数分别参照文献[14，16]。BP神经网络采用3层列文伯格-马夸尔特(Levenberg-Marquardt, LM)算法“7-15-1”的网络结构，选择Tansig函数和logsig函数作为隐藏层和输出层的传输函数，学习率设置为0.1，目标误差为0.000 1，训练最大次数1 000。CFA算法中，分别设定为1和0.2，精英群体取表现最好的前10%，惯性权重分别取1.1和0.7。IPSO-LSSVM和CFA-LSSVM两种算法的种群规模均为30，最大进化代数为100。因为智能寻优算法具有一定的随机性，因此各进行50次实验取最优值。

4.3 仿真结果及分析

使用Matlab编程进行仿真，两种时间尺度的预测结果如图4、图5所示。

由图4、图5可知，本文提出的WD-CFA- LSSVM预测方法在两种时间尺度上的预测精度均最高。为具体对误差进行量化评价，定义平均绝对误差MAE、平均相对误差MAPE及均方根误差RMSE为

依据式(23)~式(25)得到各种算法的预测误差结果如表1所示。

图4 10分钟级各预测方法结果

图5小时级各预测方法结果

表1各预测方法的误差对比

Table 1 Prediction errors of different methods

由表1可知，在10分钟级及小时级两种时间尺度的预测表现上，本文算法的平均相对误差均小于2.5%，表明预测算法的有效性。同时通过3种典型误差分析，可知本文提出的WD-DE-LSSVM方法较LSSVM、BP、IPSO-LSSVM均明显更优。WD-DE- LSSVM在预测精度表现上也很优异，但仍然劣于本文算法，同时在相同环境进行仿真发现，在CPU时间消耗上本文算法为0.025 s，WD-DE-LSSVM为0.536 s，本文方法速度更快，进一步体现了本文算法的优越性。

同时，对比10分钟级和小时级的误差数据，可知10分钟级的预测误差较小时级的误差更小。表明本文算法在小时级尺度上适应性更强。

5  结论

为提高最小二乘支持向量机的短期风速预测精度，本文提出一种基于小波变换和改进萤火虫算法对最小二乘支持向量机进行参数寻优的预测模型。通过db3小波分解和重构将原始风速序列分解为近似序列和3层细节序列，分别利用参数优化后的LSSVM进行预测。在超参数寻优中，通过引入自适应惯性权重和混沌搜索机制对基本萤火虫算法进行改进，极大地提高了萤火虫算法的收敛速度和全局寻优能力。通过实测的风电场风速数据构造10分钟级和小时级两种时间尺度的算例样本，仿真结果表明与目前预测效果较好的CV-LSSVM，IPSO-LSSVM，WD-DE-LSSVM及经典的BP神经网络预测模型相比，本文提出的风速预测模型具有更高的精度和适应性。

[1] 刘兴杰, 岑添云, 郑文书, 等. 基于模糊粗糙集与改进聚类的神经网络风速预测[J]. 中国电机工程学报, 2014, 34(19): 3162-3169.

LIU Xingjie, CEN Tianyun, ZHENG Wenshu, et al. Neural network wind speed prediction based on fuzzy rough set and improved clustering[J]. Proceedings of the CSEE, 2014, 34(19): 3162-3169.

[2] 王娟娟, 赵闻蕾, 王兴强, 等. 基于Johnson分布直接转换法的风速预测[J]. 电力自动化设备, 2014, 34(6): 20-24.

WANG Juanjuan, ZHAO Wenlei, WANG Xingqiang, et al. Wind speed prediction based on Johnson direct transformation[J]. Electric Power Automation Equipment, 2014, 34(6): 20-24.

[3] 罗文, 王莉娜. 风场短期风速预测研究[J]. 电工技术学报, 2011, 26(7): 68-74.

LUO Wen, WANG Lina. Short-term wind speed forecasting for wind farm[J]. Transactions of China Electrotechnical Society, 2011, 26(7): 68-74.

[4] 史宇伟, 潘学萍. 计及历史气象数据的短期风速预测[J]. 电力自动化设备, 2014, 34(10): 75-80.

SHI Yuwei, PAN Xueping. Short-term wind speed forecasting considering historical meteorological data[J]. Electric Power Automation Equipment, 2014, 34(10): 75-80.

[5] 丁明, 张立军, 吴义纯. 基于时间序列分析的风电场风速预测模型[J]. 电力自动化设备, 2005, 25(8): 32-34.

DING Ming, ZHANG Lijun, WU Yichun. Wind speed forecast model for wind farms based on time series analysis[J]. Electric Power Automation Equipment, 2005, 25(8): 32-34.

[6] 李文良, 卫志农, 孙国强, 等. 基于改进空间相关法和径向基神经网络的风电场短期风速分时预测模型[J]. 电力自动化设备, 2009, 29(6): 89-92.

LI Wenliang, WEI Zhinong, SUN Guoqiang, et al. Multi-interval wind speed forecast model based on improved spatial correlation and RBFneural network[J]. Electric Power Automation Equipment, 2009, 29(6): 89-92.

[7] 孙斌, 姚海涛, 刘婷. 基于高斯过程回归的短期风速预测[J]. 中国电机工程学报, 2012, 32(29): 104-109.

SUN Bin, YAO Haitao, LIU Ting. Short-term wind speed forecasting based on Gaussian process regression model[J]. Proceedings of the CSEE, 2012, 32(29): 104-109.

[8] 肖迁, 李文华, 李志刚, 等. 基于改进的小波-BP神经网络的风速和风电功率预测[J]. 电力系统保护与控制, 2014, 42(15): 80-86.

XIAO Qian, LI Wenhua, LI Zhigang, et al. Wind speed and power prediction based on improved wavelet-BP neural network[J]. Power System Protection and Control, 2014, 42(15): 80-86.

[9] 杨锡运, 孙宝君, 张新房, 等. 基于相似数据的支持向量机短期风速预测仿真研究[J]. 中国电机工程学报, 2012, 32(4): 35-41.

YANG Xiyun, SUN Baojun, ZHANG Xinfang, et al. Short-term wind speed forecasting based on support vector machine with similar data[J]. Proceedings of the CSEE, 2012, 32(4): 35-41.

[10]杜颖, 卢继平, 李青, 等. 基于最小二乘支持向量机的风电场短期风速预测[J]. 电网技术, 2008, 32(15): 62-66.

DU Ying, LU Jiping, LI Qing, et al. Short-term wind speed forecasting of wind farm based on least square-support vector machine[J]. Power System Technology, 2008, 32(15): 62-66.

[11]曾杰, 张华. 基于最小二乘支持向量机的风速预测模型[J]. 电网技术, 2009, 33(18): 144-147.

ZENG Jie, ZHANG Hua. A wind speed forecasting model based on least squares support vector machine[J]. Power System Technology, 2009, 33(18): 144-147.

[12]杨洪, 古世甫, 崔明东, 等. 基于遗传优化的最小二乘支持向量机风电场风速短期预测[J]. 电力系统保护与控制, 2011, 35(11): 44-48.

YANG Hong, GU Shifu, CUI Mingdong, et al. Forecast of short-term wind speed in wind farms based on GA optimized LS-SVM[J]. Power System Protection and Control, 2011, 35(11): 44-48.

[13] 孙斌, 姚海涛. 基于PSO优化LSSVM的短期风速预测[J]. 电力系统保护与控制, 2012, 40(5): 85-89.

SUN Bin, YAO Haitao. The short-term wind speed forecast analysis based on the PSO-LSSVM predict model[J]. Power System Protection and Control, 2012, 40(5): 85-89.

[14] 王贺, 胡志坚, 张翌晖, 等. 基于IPSO-LSSVM的风电功率短期预测研究[J]. 电力系统保护与控制, 2012, 40(24): 107-112.

WANG He, HU Zhijian, ZHANG Yihui, et al. Short-term prediction of wind power based on IPSO-LSSVM[J]. Power System Protection and Control, 2012, 40(24): 107-112.

[15] 王贺, 胡志坚, 张翌晖, 等. 基于聚类经验模态分解和最小二乘支持向量机的短期风速组合预测[J]. 电工技术学报, 2014, 29(4): 237-245.

WANG He, HU Zhijian, ZHANG Yihui, et al. A hybrid model for short-term wind speed forecasting based on ensemble empirical mode decomposition and least squares support vector machines[J]. Transactions of China Electrotechnical Society, 2014, 29(4): 237-245.

[16] 彭春华, 刘刚, 孙惠娟. 基于小波分解和微分进化支持向量机的风电场风速预测[J]. 电力自动化设备, 2012, 32(1): 9-13.

PENG Chunhua, LIU Gang, SUN Huijuan. Wind speed forecasting based on wavelet decomposition and differential evolution-support vector machine for wind farms[J]. Electric Power Automation Equipment, 2012, 32(1): 9-13.

[17] 田中大, 李树江, 王艳红, 等. 基于小波变换的风电场短期风速组合预测[J]. 电工技术学报, 2015, 30(9): 112-120.

TIAN Zhongda, LI Shujiang, WANG Yanhong, et al. Short-term wind speed combined prediction for wind farms based on wavelet transfer[J]. Transactions of China Electro technical Society, 2015, 30(9): 112-120.

[18] MALLAT S G. A theory for multi-resolution signal decomposition: the wavelet representation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1989, 11(7): 674-693.

[19] 唐杰明, 刘俊勇, 杨可, 等. 基于灰色模型和最小二乘支持向量机的电力短期负荷组合预测[J]. 电网技术, 2009, 33(3): 63-68.

TANG Jieming, LIU Junyong, YANG Ke, et al. Short-termload combination forecasting by grey model and least square support vector machine[J]. Power System Technology, 2009, 33(3): 63-68.

[20] 曾鸣, 吕春泉, 田廓, 等. 基于细菌群落趋药性优化的最小二乘支持向量机短期负荷预测方法[J]. 中国电机工程学报, 2011, 31(34): 93-99, 11.

ZENG Ming, LÜ Chunquan, TIAN Guo, et al. Least squares-support vector machine load forecasting approach optimized by bacterial colony chemo taxis method[J]. Proceedings of the CSEE, 2011, 31(34): 93-99, 11.

[21] 傅美平, 马红伟, 毛建容. 基于相似日和最小二乘支持向量机的光伏发电短期预测[J]. 电力系统保护与控制, 2012, 40(16): 65-69.

FU Meiping, MA Hongwei, MAO Jianrong. Short-term photovoltaic power forecasting based on similar days and least square support vector machine[J]. Power System Protection and Control, 2012, 40(16): 65-69.

[22] 栗然, 陈倩, 徐宏锐. 考虑相关因素的最小二乘支持向量机风速预测方法[J]. 电力系统保护与控制, 2010, 38(21): 146-151.

LI Ran, CHEN Qian, XU Hongrui. Wind speed forecasting method based on LS-SVM considering the related factors[J]. Power System Protection and Control, 2010, 38(21): 146-151.

[23] YANG Xinshe. Nature-inspired matheuristic algorithms[M]. UK: Lunvier Press, 2008.

[24] LUKASIK S, ZAK S. Firefly algorithm for continuous constrained optimization tasks[C] // ICCCC 2009: 97-100.

[25] 程声烽, 程小华, 杨露. 基于改进粒子群算法的小波神经网络在变压器故障诊断中的应用[J]. 电力系统保护与控制, 2014, 42(19): 37-42.

CHENG Shengfeng, CHENG Xiaohua, YANG Lu. Application of wavelet neural network with improved particle swarm optimization algorithm in power transformer fault diagnosis[J]. Power System Protection and Control, 2014, 42(19): 37-42.

[26] 程泽, 董梦男, 杨添剀, 等. 基于自适应混沌粒子群算法的光伏电池模型参数辨识[J]. 电工技术学报, 2014, 29(9): 245-252.

CHENG Ze, DONG Mengnan, YANG Tiankai, et al. Extraction of solar cell model parameters based on self- adaptive chaos particle swarm optimization algorithm[J]. Transactions of China Electrotechnical Society, 2014, 29(9): 245-252.

[27] 易谷, 王清蓉. 基于CPSO-RLS的电力系统谐波估计融合算法[J]. 电力系统保护与控制, 2014, 42(12): 25-29.

YI Gu, WANG Qingrong. Fusion algorithm of harmonic estimation based on CPSO-RLS for power system[J]. Power System Protection and Control, 2014, 42(12): 25-29.

(编辑 葛艳娜)

Short-term wind speed forecasting based on WD-CFA-LSSVM model

FANG Biwu, LIU Dichen, WANG Bo, YAN Bingke, WANG Xunting

(School of Electrical Engineering, Wuhan University, Wuhan 430072, China)

Accurately predicting wind speed is of key importance for large scale wind power connecting to the grid. To improve the short-term wind speed forecasting accuracy, a least squares support vector machine wind speed prediction model based on wavelet decomposition and improved firefly algorithm is proposed. Firstly, the actual wind speed series is decomposed and reconstructed to approximate series and detail series, then the series are separately predicted by LSSVM optimized by chaotic firefly algorithm, at last the separate prediction series are superposed as the ultimate prediction wind speed. To verify the proposed model, two different time scale actual wind speed data are applied to simulation. The results show that the proposed model has higher prediction accuracy than classical model like CV-LSSVM, IPSO-LSSVM, WD-DE-LSSVM and BP neural networks, showing its validity and superiority.

This work is supported by National Natural Science Foundation of China (No. 51477121 and No. 51207113).

short-term wind speed forecasting; wavelet decomposition and reconstruction; chaotic firefly algorithm; least squares support vector machines

10.7667/PSPC150925

2015-06-03；

2015-07-16

方必武(1991-)，男，硕士研究生，研究方向为风电消纳与负荷调度；E-mail: bwfwhu@163.com

刘涤尘(1959-)，男，教授，博导，研究方向为电力系统运行与控制；

王 波(1978-)，男，副教授，研究方向为源荷协调及其高级应用。

国家自然科学基金资助项目(51477121，51207113)