覆冰情况下输电线路有限元计算及其结构优化
王 燕,皇甫成,杜志叶,阮江军
覆冰情况下输电线路有限元计算及其结构优化
王 燕1,皇甫成2,杜志叶1,阮江军1
(1.武汉大学电气工程学院,湖北 武汉 430072;2.国网冀北电力有限公司,北京 100053)
建立了塔-线耦合结构系统三维有限元力学计算模型。通过对覆冰输电线路耐张段位移及应力分布情况进行分析计算,提出了线路耐张段在一定风速与覆冰厚度条件下的临界失效曲线。经过多次计算并验证薄弱杆塔以及薄弱单元分布情况,得到了薄弱位置的分布特点和规律。以发生覆冰倒塔事故的实际线路为研究对象,并以力学分析计算结果为依据,提出了有针对性地更换杆塔最薄弱处钢材以及在耐张段内薄弱处增加一基杆塔的线路改进方案。通过结构优化前后线路耐张段薄弱单元应力比值以及临界失效曲线的对比分析,证明了所提出改进方案的正确性和有效性。
塔-线系统;有限元计算;覆冰;临界失效曲线;结构优化
0 引言
高压输电线路的导线、地线和绝缘子覆冰在一定程度上影响了塔-线系统的结构稳定性,对输电线路的安全稳定运行造成影响。由此导致的事故具有以下特点:(1) 输电线路破坏严重,事发地气候条件恶劣,抢修难度大,耗时长;(2) 事故波及面广,可能出现整片区域输电线路损毁的情况;(3) 如果交叉跨越处发生事故,可能导致铁路和公路交通受阻,社会影响较大。因此对高压输电线路承受覆冰荷载和风荷载条件下的力学稳定性进行计算,并据此提出结构改进方案具有重要意义[1-8]。
近年来,国内外诸多科研工作者和研究机构对覆冰输电线路数值计算进行了研究[9-11],但由于塔-线系统为强非线性耦联系统,且受到覆冰厚度和风力等因素影响,建立精细的有限元计算模型进行数值分析较为复杂。
数值分析方面,文献[12]通过对两组单、双塔段结构件模拟极限覆冰荷载下的加载试验和有限元分析,得到约束交叉斜撑的面外变形是提高整体结构抗冰承载力主要途径的结论;文献[13]提出了在风荷载下的塔线系统解析数值模型,应用该模型计算得到的数据用于分析塔线系统的动态特性和失效机理;文献[14]建立了多跨塔-线系统的二维有限元数值计算模型,分析了脱冰和断线等情况下,输电线路的杆塔和导线动力响应方面的问题;文献[15]对不平衡张力经典算法中存在的收敛速度慢、收敛于非正确解等问题提出解决办法,对在不同覆冰厚度情况下的不平衡张力进行了计算。以上文献在材料非线性以及考虑塔-线系统耦合特性的数值模型建立、分析方面还存在欠缺。
结构优化方面,文献[16]在总结输电线路典型覆冰事故的基础上,对输电线路覆冰事故特点、事故原因及防治技术措施进行了总结分析;文献[17]建立了以静力学力矩平衡为理论依据的架空输电线路综合荷载等值覆冰厚度预测模型,并通过试验验证了模型的精准性;文献[18]建立了以猫头直线塔为基础的“三线两塔”输电塔线体系耦合有限元模型,研究了风向角、覆冰风攻角和风速对输电塔线体系静态承载能力的影响。以上文献在输电塔-线系统的研究方面取得了较好的成果,但或未对塔-线系统提出具体改进措施,或未对改进措施进行详细论证分析。
本文以某实际同塔双回线路为例,首先建立了其单塔有限元力学计算模型,并以此为基础建立耐张段模型;计算了不同风速和覆冰情况下耐张段的位移情况及其临界失效曲线,输出了薄弱单元及薄弱杆塔;最后以某实际发生倒塔的线路为研究对象,提出了线路结构改进方案,对现有输电线路设计、管理以及运维人员进行防冰、抗冰工作提供参考,提高输电线路防覆冰安全运行能力。
1 输电线路有限元计算模型
1.1 塔-线结构系统计算模型
高压输电线路塔-线结构系统为典型的单索体系,高压架空四分裂导线可等效为一根悬索,具有大位移小应变的几何特性[19],其等效直径以式(1)进行计算。
式中:为分裂根数;为分裂直径;为导体直径。
式(2)为导线悬链线数学模型,据此可以得到悬链线上各离散节点的坐标,同时通过调节和0值大小,可调整线路的弧垂。
式中:为两悬挂点的水平距离;为两悬挂点的垂直距离;为单位长度导线所受重力与导线截面的比值;0为导线最低点的应力。
为精确计算多档距高压输电线路塔-线系统的档距、高差和不均匀负荷导致的应力和形变,有限元模型建模所应用的力学单元如图1所示,其中:LINK10截面为四边形,用以模拟导、地线的悬链线模型;采用BEAM188模拟杆塔使用Q345和Q235两种型号的角钢,通过设定188单元的实常数来模拟L形角钢的形状及其截面尺寸;采用梁单元BEAM188的ctube模型模拟覆冰[20]。

图1 力学单元应用示意图
1.2 荷载的施加与计算
导地线水平档距为H时,其风荷载为
对导线风荷载采用单位荷载进行施加,覆冰时,单位风荷载为
式中:为风压不均匀系数;sc为体型系数;c为风载调整系数;为设计风速;为导地线外径;为覆冰厚度;为风向与导地线轴向间夹角。
绝缘子的风荷载J为
式中:1为绝缘子串数;2为每串绝缘子的片数;p为绝缘子受风面积;z为风压高度变化系数。
导地线覆冰重力单位荷载为
=9.8×0.9π(+)×10-3(6)
式中:为导、地线外径;为覆冰厚度。
式中:为构件数目;为覆冰密度;h为覆冰直径随高度变化系数;l为单个构件长度。
2 覆冰线路力学计算
以某实际运行的500 kV同塔双回线路为例,结合途经区域微气候带的地形地貌、杆塔结构及环境因素等特征,对各基杆塔进行逐塔逐档距分析,进而得到各杆塔和易发生覆冰事故1-2个耐张段内的力学分析计算结果,为制定防覆冰结构改进方案奠定基础。
2.1 单塔有限元计算
首先建立一塔两线系统计算模型,为后续耐张段模型的建立奠定基础。以覆冰荷载和风荷载为基本荷载,导线覆冰时,根据覆冰质量及导地线覆冰重力单位荷载计算公式计算出力荷载施加在相应的节点上。风荷载可用不同高度处的平均风速计算得到,对于杆塔的不同高度,平均风速用指数函数来描述[20]。风力对杆塔覆冰时整体受力情况有较大影响,且风的方向比较随机,本文仅考虑如图2所示横向风荷载情况下逆转角方向风速和顺转角方向风速两种风向,即沿Z-方向和Z+方向。

图2输电线路典型风向示意图
按前文所述方法建立该线路28#杆塔的塔-线系统有限元计算模型,风速从0~30 m/s、覆冰厚度从0~30 mm进行循环计算,按照前文所述加载方法,对导、地线及杆塔进行加载,杆塔塔基计算时认为是固点,对各塔基节点所有自由度均施加约束。为平衡输电塔顺导线方向的张力载荷,对两端输电塔上绝缘子(或横担)与导线连接处的结点施加顺导线方向约束。
图3所示为28#杆塔模型应力分布有限元计算结果示意图,计算结果表明,随着荷载的增大应力值逐步增大且在465~500、1 026~1 060、1 590~1 630及2 150~2 190四个位置的单元应力出现较大值,这四个位置对应于杆塔的塔腿部分。28#杆塔最大轴向应力随覆冰和风速变化的曲线如图4所示,在风速一定时,随着覆冰厚度在10~22 mm之间逐渐增加,杆塔的轴向应力逐渐增大;在覆冰厚度保持不变,随着风速的增加杆塔的轴向应力也逐渐增大。

图3 28#杆塔模型有限元计算结果

图4 28#杆塔轴向应力最大值随覆冰增长变化曲线图
2.2 耐张段有限元计算
该线路在地形上以高山大岭和山地为主,其丘陵占17%、山区占45%、高山占38%,具有复杂气候环境的山区、高山地区是线路覆冰多发地域。
从表1所示耐张段相关数据分析,各基杆塔之间相对高差均较大,最大达到144.85 m,同时存在大档距,最大档距达到654 m,其所处区域地势起伏较大,地形较为复杂。以该实际耐张段线路为例建立其整体有限元计算模型,模型中杆塔、绝缘子、导地线所采用的单元与一塔两线系统完全相同,即可以调用一塔两线分析所采用的杆塔模型数据,然后根据表1所示线路实际档距、高差等结构参数,用导地线将各基杆塔有效连接,建立如图5所示模型。
2.3 耐张段主体位移分析
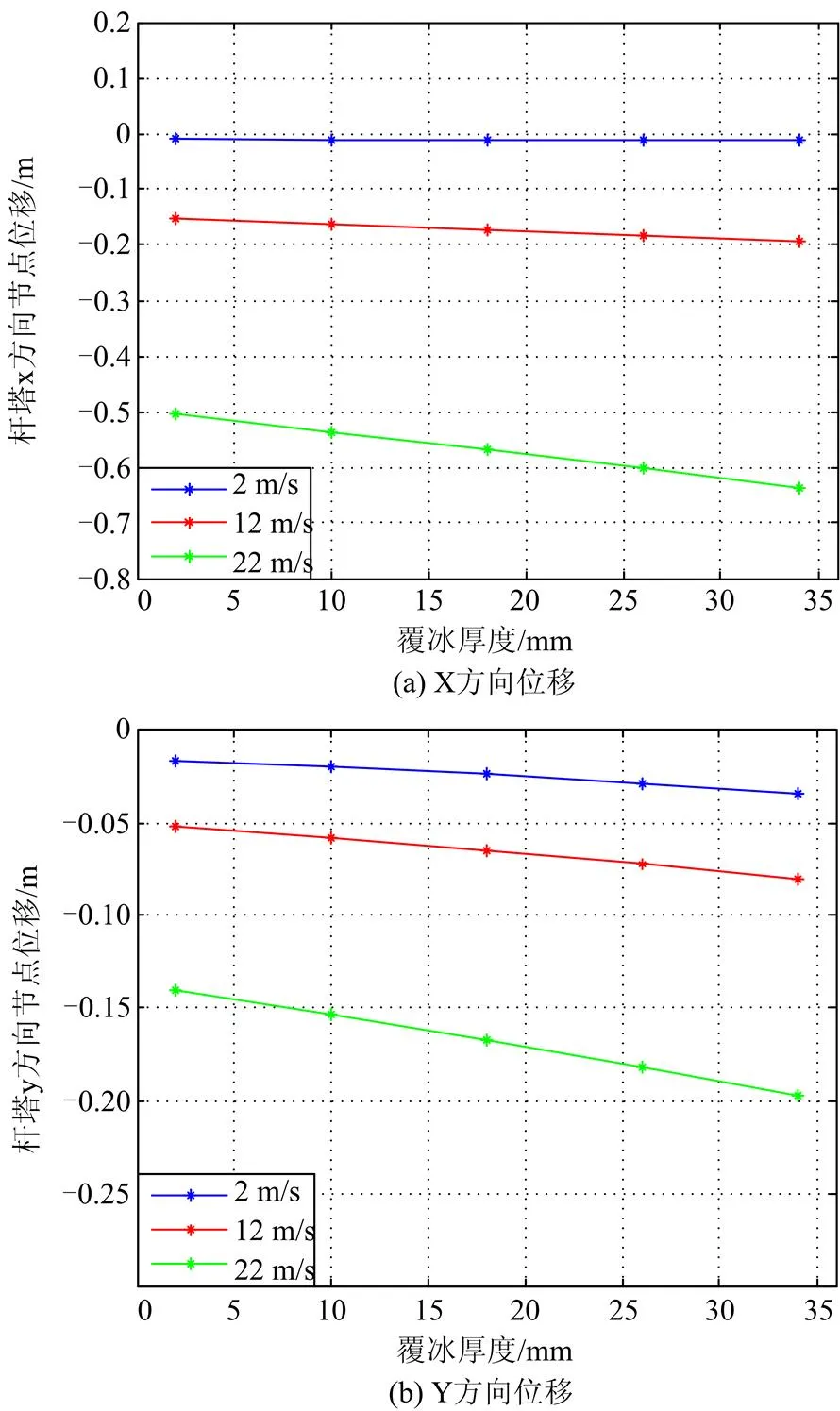
图6所示为杆塔节点在风速作用下,位移随覆冰厚度变化曲线图。从图中可以得出,X,Y方向位移与覆冰厚度呈线性关系,Z方向位移随着覆冰厚度的增大而增大,覆冰厚度越大,位移变化得越快。节点合位移与覆冰厚度也呈单调增加关系,随着覆冰厚度的增加而增大,与构件轴向应力变化趋势一致。

表1 耐张段模型参数

图5 同塔双回线路耐张段模型
2.4 安全裕度计算
安全裕度设计的关键在于安全裕度的计算,对于实际问题,准确地确定失效评定曲线和求解安全裕度数值是安全评定的必要条件[21-22]。
经过多次求解计算,在风速为0~30 m/s,覆冰厚度为0~30 mm区间内计算耐张段塔线耦合系统受力情况,得出整个耐张段内杆塔、导地线所受应力以及构件位移分布,用于杆塔薄弱位置的分析研究。为更直观描述耐张段在不同风速和覆冰厚度条件下杆塔的抵抗能力,根据杆塔临界情况下的风速与覆冰厚度,将获得的数据作为函数关系的因变量,通过回归分析,对仿真结果数据进行拟合,绘出失效评定曲线,得到式(8)所示耐张段安全裕度表达式。
2.5 耐张段薄弱点及薄弱塔输出
通过上述求解,可以得到在耐张段中各节点的位移以及各单元所受应力情况,以及在特定环境条件下(风速、冰厚)耐张段内最薄弱杆塔部件,进而找出最薄弱杆塔。
以风速24 m/s、覆冰厚度10 mm情况为例,根据计算结果得出该耐张段薄弱杆塔为26#和28#杆塔,其应力分布及薄弱位置如图8所示。从双回线路薄弱位置示意图可以得出,双回线路薄弱位置主要位于塔下部的塔腿位置。同时对比应力分布图,薄弱位置基本与应力绝对值较大位置重合。

图8 杆塔薄弱位置分布示意图
3 输电线路结构改进设计
为综合考虑同塔双回线路不同地域间的受力特性,选取在2008年因覆冰发生倒塔事故的某线路,应用前文提出的方法进行建模计算分析,提出结构改进设计方案并进行验证。研究线路涉及9基杆塔8个档距,其相关参数如表2所示。

表2 同塔双回线路参数
3.1改进方案一
选取较大风速、较大冰厚条件下的杆塔薄弱点作为参照,获取耐张段模型结构薄弱点。在不同边界气候条件下,同塔双回耐张段塔线系统模型的薄弱单元都主要集中在316号和317号塔,可以认为这两基杆塔是整个耐张段内最薄弱的杆塔。针对上述薄弱位置选取在冰厚20 mm,风速24 m/s条件下耐张段最薄弱的10个单元进行结构改进,该条件下最薄弱10个单元的相关信息如表3所示。

表3 杆塔薄弱单元计算结果
从表3可以得出杆塔薄弱处钢构主要是Q345号钢材,在杆塔设计中,一般都采用Q235、Q345和Q420这三种强度的钢材,在此选取Q420来替换薄弱处Q345钢材。通过与之前相同的加载求解方式,得出此种情况下同塔双回耐张段薄弱位置受力情况。
图9所示为改造前后薄弱单元应力比值对比图,通过有针对性地替换局部Q345钢材为Q420钢材,耐张段最大应力比值从0.956 9下降为0.863 9,说明提高局部钢材的强度能够改变耐张段结构的薄弱位置分布,使得较高强度的钢材承受更大应力,从而更充分发挥高强度材料的作用。
图10所示为替换Q420钢材后耐张段临界曲线与原有曲线对比,提高局部钢材强度后,耐张段的临界曲线所包含的范围得到扩大,在相同冰厚条件下,线路承受的最大风速提高了2 m/s左右。

图9 薄弱单元应力比值示意图

图10 耐张段临界曲线对比图
3.2改进方案二
通过前文分析可以得知,改造前该路段最薄弱位置出现在316号和317号杆塔,同时两基杆塔间档距达到1 200 m以上,在覆冰条件下产生不平衡张力较大,因此考虑在此处增加一基316+1号杆塔(塔型为SG2,呼高为36 m)的改进方案。
增加一基杆塔能够有效提高耐张段内杆塔承受外部荷载的能力,如图11所示,在相同冰厚条件下增加316+1号杆塔,路段所能承受的最大风速增加了4~6 m/s。

图11 优化前后临界曲线对比图
由图12可以得知,该改进方案能够有效降低耐张段最大应力比值。在两基薄弱杆塔之间增加新的杆塔,能够有效提高抵抗覆冰风险的能力。

图12 优化前后薄弱单元应力比值示意图
4 结论
(1) 建立了输电线路塔-线系统力学分析模型,该数值计算模型能够有效分析耐张段中各节点的位移以及各单元所受应力情况,进而精确确定耐张段内的薄弱杆塔及其部件。
(2) 通过高压输电线路结构优化前后薄弱单元应力比值以及临界曲线的对比可以得知,采用有针对性地提高薄弱部位钢材屈服强度和增加薄弱区域杆塔的改进方案,其能够承受的最大风速有所提高,线路的抗覆冰风险能力得到加强,改进效果明显。
[1] 张勇, 严承涌, 谢强. 覆冰特高压输电塔线耦联体系风致动力响应风洞试验[J]. 中国电机工程学报, 2010, 30(28): 94-99.
ZHANG Yong, YAN Chengyong, XIE Qiang. Wind tunnel test on wind-induced dynamic responses of icing ultra high voltage transmission tower-line coupling system[J].Proceedings of the CSEE, 2010, 30(28): 94-99.
[2] 王少华. 输电线路覆冰导线舞动及其对塔线体系力学特性影响的研究[D]. 重庆: 重庆大学, 2008.
WANG Shaohua. Study on iced conductor galloping and influence on dynamic properties of transmission tower-line system[D]. Chongqing:Chongqing University, 2008.
[3] FARZANEH M, SAVADJIEV K. Statistical analysis of field data for precipitation icing accretion on overhead power lines[J]. IEEE Transactions on Power Delivery, 2005, 20(2): 1080-1087.
[4] 李成榕, 吕玉珍, 崔翔, 等. 冰雪灾害条件下我国电网安全运行面临的问题[J]. 电网技术, 2008, 32(4): 14-22.
LI Chengrong, LÜ Yuzhen, CUI Xiang, et al. Research issues for safe operation of power grid in China under ice-snow disasters[J]. Power System Technology, 2008, 32(4): 14-22.
[5] 王少华, 蒋兴良, 孙才新. 覆冰导线舞动特性及其引起的导线动态张力[J]. 电工技术学报, 2010, 25(1): 159-166.
WANG Shaohua, JIANG Xingliang, SUN Caixin. Characteristics of icing conductor galloping and induced dynamic tensile force of the conductor[J]. Transactions of China Electrotechnical Society, 2010, 25(1): 159-166.
[6] 何宣虎, 王玮, 倪平浩, 等. 基于温度和倾角测量的供电线路覆冰在线监测研究[J]. 电力系统保护与控制, 2014, 51(14): 62-66.
HE Xuanhu, WANG Wei, NI Pinghao, et al. Research on temperature and inclination measurement based icing online monitoring of power supply line[J]. Power System Protection and Control, 2014, 51(14): 62-66.
[7] 陆佳政, 朱思国, 李波, 等. 特高压输电线路直流融冰变流系统设计[J]. 电力系统保护与控制, 2014, 42(11): 124-129.
LU Jiazheng, ZHU Siguo, LI Bo, et al. DC ice-melting converter system design for EHV transmission line[J]. Power System Protection and Control, 2014, 42(11): 124-129.
[8] 马冰, 陈忠华, 刘红恩, 等. 高压大功率电网新型 MMC-STATCOM 结构直流融冰装置研究[J]. 电力系统保护与控制, 2014, 43(11): 101-108.
MA Bing, CHEN Zhonghua, LIU Hongen, et al. Research of high voltage high power grid DC ice melting and static synchronous compensation device[J]. Power System Protection and Control, 2014, 43(11): 101-108.
[9] 黄文焘, 邰能灵, 范春菊. 基于杆塔结构力学测量的线路覆冰在线监测系统研究[J]. 电力系统保护与控制, 2012, 40(24): 71-83.
HUANG Wentao, TAI Nengling, FAN Chunju. Study on icing monitoring system of different tower overhead transmission lines based on mechanics measurements[J]. Power System Protection and Control, 2012, 40(24): 71-83.
[10]陈金熠, 范春菊, 胡天强, 等. 考虑架空输电线路状态的线路覆冰监测系统的研究[J]. 电力系统保护与控制, 2012, 40(15): 93-98.
CHEN Jinyi, FAN Chunju, HU Tianqiang, et al. Study on monitoring system of transmission line icing considering the state of overhead transmission lines[J]. Power System Protection and Control, 2012, 40(15): 93-98.
[11]段涛, 罗毅, 施琳, 等. 计及气象因素的输电线路故障概率的适时评估模型[J]. 电力系统保护与控制, 2013, 41(15): 59-67.
DUAN Tao, LUO Yi, SHI Lin, et al. A real-time fault probability evaluation model of transmission line considering meteorological factors[J]. Power System Protection and Control, 2013, 41(15): 59-67.
[12]谢强, 孙力. 覆冰荷载作用下500 kV输电杆塔结构破坏机理试验分析[J]. 高电压技术, 2010, 36(12): 3090-3096.
XIE Qiang, SUN Li. Experimental analysis on failure mechanism of 500 kV transmission tower under ice loading[J]. High Voltage Engineering, 2010, 36(12): 3090-3096.
[13] BATTISTA R C, RODRIGUES R S, PFEIL M S. Dynamic behavior and stability of transmission line towers under wind forces[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2003(91): 1051-1067.
[14] MCCLURE G, LAPOINTE M. Modeling the structural dynamic response of overhead transmission lines[J]. Computers & Structures, 2003(81): 825-834.
[15]宋刚, 张彤. 特高压直流输电线路直线塔重覆冰不平衡张力计算[J]. 电力自动化设备, 2014, 34(7): 119-123.
SONG Gang, ZHANG Tong. Unbalanced tension calculation of UHVDC transmission lines and suspension towers with heavy ice-coating[J]. Electric Power Automation Equipment, 2014, 34(7): 119-123.
[16]王少华. 输电线路典型覆冰事故及防治技术分析[J]. 高压电器, 2010, 46(10): 85-89.
WANG Shaohua. Analysis of typical ice accidents of transmission lines and presenting techniques[J]. High Voltage Apparatus, 2010, 46(10): 85-89.
[17]蒋兴良, 常恒, 胡琴, 等. 输电线路综合荷载等值覆冰厚度预测与试验研究[J]. 中国电机工程学报, 2013, 33(10): 177-183.
JIANG Xingliang, CHANG Heng, HU Qin, et al. Prediction and experimental study on combined load equivalent ice thickness of overhead transmission line[J]. Proceedings of the CSEE, 2013, 33(10): 177-183.
[18]彭家宁, 张栋梁, 赵高煜, 等. 覆冰输电塔线体系风载荷影响因素分析[J]. 固体力学学报, 2014, 35(增刊1): 208-214.
PENG Jianing, ZHANG Dongliang, ZHAO Gaoyu, et al. Analysis on influencing factors of wind load of iced transmission tower-line system[J]. Chinese Journal of Solid Mechanics, 2014, 35(S1): 208-214.
[19]彭迎, 阮江军. 模拟电荷法计算特高压架空线路3维工频电场[J]. 高电压技术, 2006, 32(12): 69-74.
PENG Ying, RUAN Jiangjun. Calculation of three- dimensional harmonic electric field around ultra high voltage overhead line based on the charge simulation method[J]. High Voltage Engineering, 2006, 32(12): 69-74.
[20]曹枚根, 徐忠根. 钢管组合大跨越输电塔导地线耦合效应研究[J]. 中国电力, 2006, 39(12): 36-39.
CAO Meigen, XU Zhonggen. Research on cables coupled effect of combo steel tube tower for large crossing transmission lines[J]. Electric Power, 2006, 39(12): 36-39.
[21]杜志叶, 张宇, 阮江军, 等. 500 kV架空输电线路覆冰失效有限元仿真分析[J]. 高电压技术, 2012, 38(9): 2430-2436.
DU Zhiye, ZHANG Yu, RUAN Jiangjun, et al. Failure analysis of 500 kV iced overhead transmission line by finite element method[J]. High Voltage Engineering, 2012, 38(9): 2430-2436.
[22]杜志明, 范军政. 安全裕度研究与应用进展[J]. 中国安全科学学报, 2004, 14(6): 6-10.
DU Zhiming, FAN Junzheng. Progress in study and application of safety margin[J]. China Safety Science Journal, 2004, 14(6): 6-10.
(编辑 葛艳娜)
Finite element calculation and structural optimization method for the high voltage transmission line under icing condition
WANG Yan1, HUANGFU Cheng2, DU Zhiye1, RUAN Jiangjun1
(1. School of Electrical Engineering, Wuhan University, Wuhan 430072, China; 2. State Grid Jibei Electric Power Company, Beijing 100053, China)
This paper proposes a 3D finite element mechanical calculation model of tower-line coupling system. Based on the analysis of the displacement and stress distribution of the strain section that under wind and icing condition, the safety margin curve under definite ice thickness and wind speed condition is proposed. As a result of calculated and verified the weak tower and weak elements of the tower, the characteristic of the weak position distribution is obtained. A working transmission line which happening a tower collapse accident is the subject investigated. The application of the mechanical calculation results to analyze the optimizing scheme of the operational transmission line, the methods that replace the steel type of the tower weak elements and add a tower in weak position of the strain section are proposed. Both the comparison critical curve of the strain section and the comparison curve of the tower weak elements stress ratio demonstrate the validity of the improved corrective recommendations.
tower-line system; finite element calculation; icing; critical failure curve; structural optimization
10.7667/PSPC150624
2015-04-15;
2015-08-24
王 燕(1981-),女,高级工程师,从事电磁场数值计算、高电压与绝缘技术等方面的研究工作;
皇甫成(1981-),男,通信作者,高级工程师,从事高压直流输电、高电压与绝缘技术等方面的研究工作;E-mail:chenghuangfu@163.com
杜志叶(1974-),男,博士,副教授,从事电磁场数值计算、高电压与绝缘技术、电磁无损检测等方面的研究工作。

