CVaR和EVaR安全运行风险管理下的电力系统经济调度

易国伟，童小娇，周 鹏，翟云峰，叶中行



CVaR和EVaR安全运行风险管理下的电力系统经济调度

易国伟，童小娇，周 鹏，翟云峰，叶中行

(长沙理工大学电气与信息工程学院，湖南 长沙410004)

针对风能入网给电网安全稳定运行带来的影响，基于风险管理方法和随机优化建模理论构建了考虑线路安全风险约束的经济调度模型。为了量化和限制风电随机性对系统安全性的影响，分别采用条件风险价值(conditional value-at-risk，CVaR)和熵风险价值(entropic value-at-risk，EVaR)来刻画电网的安全裕度，通过对安全裕度指标进行风险裕度门槛值限制作为系统的安全风险约束，并运用随机模拟方法将系统安全风险约束转换为确定性的凸约束形式。最后通过对IEEE 30节点的数值仿真验证了模型的合理性和方法的有效性，综合比较了不同安全裕度和置信水平下的调度结果以及两种安全裕度风险价值刻画方法的差别。

条件风险价值；熵风险价值；安全运行风险约束；安全裕度；安全经济调度

0 引言

保证线路的安全稳定运行、防止线路功率潮流越限是在电力系统有功经济调度时需要重点考虑的方面。传统的安全经济调度在给定的负荷预测值下合理安排机组出力，使电网线路有功潮流不发生越限，从而建立确定形式的经济调度模型[1]。随着传统化石能源供应紧张，风能等可再生能源得到了大规模开发与应用[2-3]，风能应用于电力系统一方面缓解了能源紧张，而另一方面风电的随机波动性导致相关线路的潮流波动[4]，给系统安全经济调度带来了极大的挑战。

考虑风电不确定性因素的经济调度问题成为研究热点[5]。针对风电接入给系统线路安全带来的影响，一些文献采用确定性风电出力形式描述线路安全，这种方式很难反映系统的真实运行情况[6-7]。而采用概率形式来描述系统的风险约束[2-3]能够比较真实反映风电波动性对系统安全及调度结果的影响。目前在不确定环境下系统经济调度采用的最多的方法就是用机会约束刻画系统安全运行限制。文献[8]采用机会约束形式刻画电网在正常情况和发电机-1情况下的安全风险，建立了考虑备用容量优化分配的调度模型；文献[9]基于机会约束刻画线路安全风险，利用序列运算理论求解概率性约束。另一方面，机会约束存在求解复杂、运算量大的弊端，特别在数学上的非凸性给优化模型求解带来困难；同时机会约束对系统安全风险量化指标没有明确的描述[10-11]。基于此，文献[11]应用经济学中的条件风险价值(conditional value-at-risk，CVaR)刻画系统的安全风险，该方法充分利用CVaR良好的数学性质对系统不确定因素下的安全风险进行量化处理[10-11]，构建了电力系统条件风险调度模型。

本文在文献[11]的基础上分别采用经济学领域中CVaR和熵风险价值(entropic value-at-risk，EVaR)刻画电网安全运行裕度，通过对电网安全裕度设置风险门槛值作为系统的安全风险约束，取代一般性的机会约束形式。利用CVaR和EVaR良好的数学性质结合随机模拟方法将安全风险约束由一般性的概率风险约束转化为确定性的凸约束形式。通过对IEEE 30节点系统的数值模拟验证了模型的有效性，数值计算分析了不同的安全裕度、风险置信水平与系统经济性的关系以及线路功率限值对系统的影响，并且比较了不同安全风险刻画方法下系统的调度结果差别。

1  VaR、CVaR和EVaR的数学描述

1.1 VaR的数学描述

考虑数学上的不等式约束问题(,)£,其中随机变量的概率密度函数为()。则不等式成立的累积分布函数为

文献[12]中，风险价值(value-at-risk，VaR)可以表示为

VaR表示的是在给定的置信水平下，累积分布函数满足置信水平下的最小的风险值。VaR将不确定性的影响由概率性指标量化为带风险置信水平的数值性指标，但是VaR是建立在概率计算的基础上，没有考虑概率约束不满足下的超额损失部分，对尾部风险识别不准确，且其计算也比较复杂[11-12],这些局限了VaR方法在实际中的应用。

1.2 CVaR的数学描述

文献[12-13]提出了CVaR(conditional value-at- risk)风险度量方法，CVaR在VaR的基础上考虑到了超额风险损失的平均水平，其与VaR的数学关系可以表示为

数学上CVaR的表达式如下[13]

式(4)计算复杂，文献[13]引入一个等价的连续凸函数(,)来计算CVaR()

且有：

实际计算中，对于(,)函数中的积分项，采用样本平均法进行近似。设为来自随机变量的样本点，为样本点数，则(,)相应的近似凸函数表示为[13]

相比VaR计算复杂,式(6)、式(7)对CVaR的计算提供了很大的方便，同时由文献[13]知，式(6)的最优解∗=VaR()。

1.3 EVaR的数学描述

基于VaR和CVaR的研究，文献[14]提出了一种新的风险度量方法—EVaR(entropic value-at -risk)，定义如下：

对任意常数，切比雪夫不等式有

其中，M(x,)(z)表示的是(,)的矩生成函数，其表达式为

(9)

解方程e-z×aM(x,)(z)=1-可得[14]

式(8)变为：Pr((,)³a(x,)(1-b,z))£1-b，这与式(2)中的Pr((,)£)³的表达形式互补。由式(10)，EVaR定义为[14]

EVaR具有凸性和连续性等一些优良特征，且其计算也容易实现。对于M(x,)(z)中含有的积分项，采用样本平均法近似，其近似函数表示为[14]

1.4 VaR、CVaR、EVaR的数学关系

CVaR和EVaR采用带风险置信水平的数值性指标量化不确定性的影响，通过对其进行风险槛值数值限制作为不等式约束。CVaR和EVaR不仅具有凸性、连续性等良好数学性质，而且由式(7)、式(12)知，其计算易于实现。

CVaR在VaR的基础上考虑了超额风险损失的平均水平，很显然，VaR()£CVaR()。由文献[14]中的定理3.2可知，EVaR是CVaR、VaR的上界，因此它们三者之间的关系可以表示为

更进一步的，由文献[14]中的证明可知，当®1时，CVaR()=EVaR()。

2  电网安全裕度风险刻画及安全运行约束

2.1 电网安全裕度及系统运行的安全风险约束

安全裕度的概念在各个行业受到广泛重视[6]。假设系统平衡节点不含风电和负荷，W、g、d分别为风电注入功率列向量、不含平衡节点的常规机组注入功率列向量、负荷注入功率列向量，其中g为系统调度的决策变量，W为随机变量，其概率密度函数为(W)。考虑线路电流有功潮流传输为电网安全运行目标，定义电网安全裕度为

式中：(g,W)为电网的安全裕度；(g+W-d)是第条支路在某个确定调度方案下的支路潮流；为第条支路节点灵敏度系数向量，由直流潮流法求得[11,15]；P,max为第条支路的最大传输功率限值；为支路总数。

由式(14)可以看出，保证电网安全运行的参考安全裕度的取值范围为[-1,0]。(g,W)=0时，表示电网中至少已有一条线路功率已经达到其功率上限值；(g,W)=-1时，表示电网中的所有线路功率均为0。所以，(g,W)£0是电网安全运行的必要条件。

裕度函数(g,W)中含有随机变量W，需要用概率方法进行处理，电网的安全约束通常采用机会约束的形式，表达为[8-9]

式中：-为电网安全裕度槛值；为电网安全的风险置信水平，反映的是约束满足的置信程度。

基于上节中的风险管理方法的分析，本文分别采用CVaR与EVaR法来刻画电网的安全裕度，替代式(15)中描述，并用不等式形式给出电网的安全运行风险约束。

2.2 CVaR安全裕度及安全风险约束

定义电网的CVaR安全裕度CVaR(g)如式(16)

式中，W,k为风电出力的样本点，可根据其概率分布函数由随机模拟法获得，具体过程参见文献[2]。

由此，系统的安全风险约束为

式中，为(0,1)中的常数，表示风险裕度槛值。

2.3 EVaR安全裕度及安全风险约束

基于前面的研究，定义电网的EVaR安全裕度EVaR(g)为

相应的，此时的系统安全风险约束为

2.4 两类安全裕度风险刻画方法说明及比较

结合前面的数学理论部分，电网的CVaR安全裕度和电网的EVaR安全裕度都采用带风险置信水平的数值指标来量化风电的不确定性对电网安全的影响，同时考虑了风险价值的尾部损失风险，更符合实际系统运行要求[11]。式(17)、式(19)采用常规数值不等式形式描述系统的安全风险约束，替代一般性的机会约束形式，使约束求解简化。

进一步，由1.4节数学比较关系可得出如下结论：在相同的和下，CVaR安全裕度因考虑了风险价值的尾部风险，因此对系统而言，式(17)刻画的安全性比式(15)刻画的安全性要高；而由EVaR和CVaR的数学关系结论可知，式(19)的安全性比式(17)的安全性更高，且在®1时，两者的安全性程度近似相同。

3  安全运行风险约束下的调度建模及计算

3.1 考虑安全风险约束的调度模型

3.1.1目标函数

不计风电发电成本，含风电系统的有功经济调度以发电机组总的燃料费用最小为目标[16-17]，总的原料成本函数表达如下

式中：G为常规发电机的总的燃料成本；g0为常规机组的注入功率列向量；0、0、0为机组的发电成本系数矩阵；为元素为1的列向量，其长度与其后所乘列向量相同，下同。

3.1.2约束条件

1) 功率平衡约束。

为了避免多个机组参与调频时潮流方程难以求解，本文暂时只考虑一个调频机组，即平衡节点就是调频机组，因此(21)式可以转化为

其中，g0为平衡节点的调频机组出力。

2) 线路安全风险约束。

模型中的线路安全风险约束就是第2部分所阐述的内容。采用CVaR刻画电网的安全裕度的安全风险约束为式(17)；采用EVaR刻画电网的安全裕度的安全风险约束为式(19)。

其中，安全裕度槛值的取值范围为[0，max]，有关最大裕度槛值max的具体讨论分析见下文数值仿真部分。

3) 常规机组出力约束。

3.2 调度模型计算处理

3.2.1目标函数的计算处理

将功率平衡约束(22)代入到目标函数(20)中得

式中：、、为不含平衡节点的常规机组的发电成本系数矩阵；g0、g0、g0为平衡节点调频机组的发电成本系数。

由于目标函数G中含有随机变量W，采用确定性的表达没有意义，因此取式(24)的期望函数最小化作为新的目标函数[2]，表示为

3.2.2安全风险约束的计算处理

由优化理论可知，约束式(17)、式(19)中的决策变量、可以直接与g一起作为调度模型整体的决策变量[11,18]，因此，式(17)、式(19)中的min、inf可以直接去掉。

对于CVaR松弛线性化[11]，因样本点过多时维数过于庞大不利于计算、过少时又无法反应真实情况，因此，本文不对其进行线性化处理，直接作为常规凸约束不等式。

4  数值仿真实验

4.1 算例系统

针对IEEE 30节点6机系统进行仿真测试[8]。功率基准值设为100 MVA，发电机的所有相关参数参见文献[11]。系统的平衡节点为节点1；风电场在22节点接入系统，风电场的相关参数见文献[8]，风电预测出力为0.581 p.u.，风速波动比例参数为10%；系统总的有功功率为2.834 p.u.。为了使仿真分析容易进行，线路5-7功率限值设置为0.18 p.u.，此线路作为本文的关键线路，其它所有参数为网络标准参数。随机样本点数=1000。

4.2 系统经济性与安全裕度风险刻画方法

本文分别采用了两种数学方法刻画电网安全裕度—CVaR法和EVaR法，针对两种电网安全裕度刻画方法下的系统经济性与电网安全裕度槛值、置信水平的关系变化总图如图1所示。

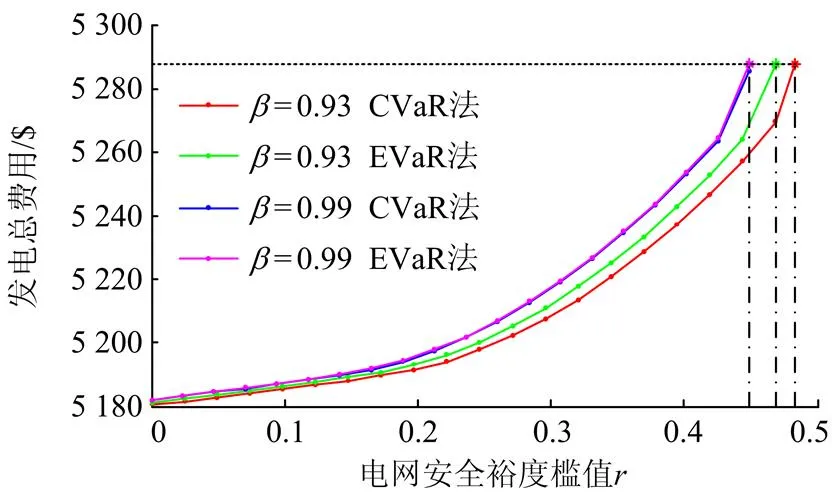
图1发电总费用随裕度槛值及风险置信水平变化曲线

图1不仅给出了两种刻画方法下等于0.93、0.99时系统经济性随的变化情况，还可看出关于两种刻画方法下的经济费用、最大安全裕度槛值max区别，同时可以发现两种方法在最大安全裕度槛值下的系统最大安全发电费用存在一定的规律。下面分别给予具体介绍。

4.2.1安全裕度槛值与经济性关系

图1给出了一个基本规律：不管是哪种刻画方法也不管置信水平取何值，随着电网安全裕度槛值的增加，系统的发电总费用均发生相应增加。这是因为随着槛值的增加，即要求电网安全裕度远离0而向-1靠近，因此就相应的增大了电网的安全性，而系统必须以牺牲经济性来换取电网安全性增加的要求。因此在调度中，需要根据实际情况，基于图1中经济性与裕度槛值之间的直观变化关系，选择合适的裕度槛值，使系统兼顾安全性和经济性要求。具体地，表1、2分别给出了置信水平=0.93、0.99下的机组调度结果及总发电费用。

表1置信水平=0.93的不同安全裕度刻画方法的调度结果

Table 1 Dispatch results of different methods of characterizing safety margin under confidence level b=0.93

表2置信水平=0.99的不同安全裕度刻画方法的调度结果

Table 2 Dispatch results of different methods of characterizing safety margin under confidence level b=0.99

进一步地，可以发现如下规律：不管置信水平取何值，针对一个固定的裕度槛值，采用EVaR法下的系统运行费用总比CVaR法要高。基于前面的理论部分，这是因为采用EVaR法刻画电网安全裕度下的电网安全性比采用CVaR法下的电网安全性要高，安全性程度越高，系统所需牺牲的经济性就越大。这个数值结论也验证了前面的理论阐述。

4.2.2 风险置信水平与经济性关系

从图1中可以发现风险置信水平对系统运行费用的影响：针对某一种刻画方法，在同一槛值下，置信水平的增加会导致系统的总运行费相应的增加。这是因为，对于同一裕度槛值，当置信水平由0.93变化为0.99时，电网的安全性要求增高，而安全性的增加会导致经济性的变差。对比表1、2 两种刻画方法下的前4行可以具体看出置信水平对系统经济性以及调度结果的影响。

观察图1进一步可以发现：针对一个确定的槛值，EVaR方法下的发电总费用比CVaR方法下发电总费用要高，但是在=0.99时两者的差别比=0.93时两者的差别要小很多，下面给予详细的分析说明。

图2分别给出了=0.44时两种安全裕度刻画方法下的发电总费用和费用差别关于风险置信水平的变化曲线。从图中可以看出，在确定的槛值下，随着置信水平的增加，不管是哪种刻画方法，系统的发电总费用均相应增加，而两种刻画方法下的系统发电总费用差别却随着的增加逐渐降低，到后面基本上看不出差别。基于前面理论说明，这是因为EVaR方法下的电网安全性比CVaR方法下的电网安全性要高，但是当®1时，两种方法下的电网安全性程度近似相同了，电网的安全性程度直接反映在了经济性上面，因此®1时，两种方法的经济差别减小为0。两种安全裕度刻画方法通过经济性反映了安全性的差别，验证了前面理论阐述。

图2发电总费用及费用差别随风险置信水平变化曲线

4.2.3最大安全裕度槛值max及最大安全运行费用

图1中的竖、横黑色虚线所对应的数值分别代表不同安全裕度刻画方法、不同风险置信水平下的电网最大安全裕度槛值max及在最大安全裕度槛值下的系统最大安全运行费用，下面给予详细讨论。

以TolCon=10^(-6)作为检验电网的安全风险约束不等式(17)(19)是否满足的临界裕值，裕度槛值以d=0.0001的步长逐渐增大，测试得到的电网在不同安全裕度刻画方法下的电网最大安全裕度槛值max以及电网在最大安全裕度槛值max下的系统最大安全运行费用随风险置信水平的变化曲线如图3所示。

图3最大安全运行费用及最大安全裕度槛值随风险置信水平变化曲线

从图3可以看出，随着置信水平的变化，采用CVaR方法下的最大安全裕度槛值总是比采用EVaR方法下的最大安全裕度槛值要大，并且在®1的时候，两种方法下的最大安全裕度值就基本相同了。这可以解释：EVaR方法提供的安全性比CVaR提供的安全性要高，因此其裕度槛值的变化范围就相应的比CVaR方法相应的要小，当®1时，两者的安全性程度相同，因此两者的裕度槛值的变化范围就基本相同了。

从图3中还可以发现：不管是CVaR方法还是EVaR方法，随着置信水平的变化，系统在各自方法所对应的最大安全裕度槛值max下的系统最大安全费用基本上是固定不变的，始终维持在5288$附近。表1、2中两种刻画方法中的第5行提供了在其相应最大安全裕度槛值下的调度结果，从调度结果可以看出，在最大安全运行费用情况下的机组调度结果基本上是相同的，不随置信水平和刻画方法的变化而变化。电网这一固定的最大安全经济费用和最安全的调度结果可以为电网的安全运行提供一些经济和调度出力参考。

4.3 关键线路功率限值对系统的影响

4.3.1关键线路功率限值对经济性影响分析

图4给出了=0.93条件下，关键线路功率限值分别为0.16 p.u.、0.18 p.u.、0.20 p.u.时，两种安全裕度刻画方法下的发电总费用随安全裕度槛值的变化曲线。从图中可以看出，适当增加电网关键线路的功率限值可以减少系统的运行费用，提高系统的经济效益；而减少关键线路功率限值会增大系统的调度运行费用，并且随着的增大，线路功率限值的增减对经济效益的影响逐渐变大。

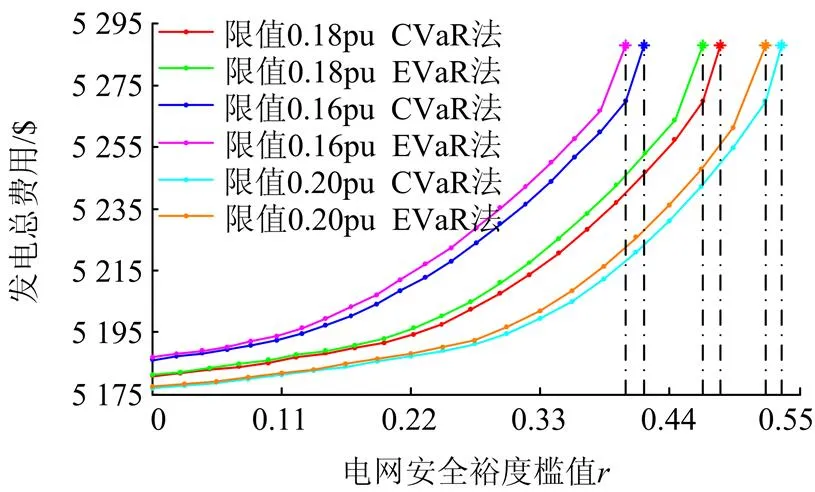
图4不同功率限值下的发电总费用随裕度槛值变化曲线

4.3.2关键线路功率限值对max影响分析

图5给出关键线路功率限值分别为0.16 p.u.、0.18 p.u.、0.20 p.u.时，两种安全裕度刻画方法下的最大安全裕度槛值max随风险置信水平的变化曲线。从图中看出，增加关键线路的功率限值能够增大电网的最大安全裕度槛值，为调度人员提供更大的取值范围，而减小关键线路功率限值会缩小的取值范围。结合图4不难发现，适当的增加关键线路的功率限值不仅能够提高电网的经济效益、减小运行成本，而且能够增大电网的裕度槛值取值范围，提供更高的电网的安全性。

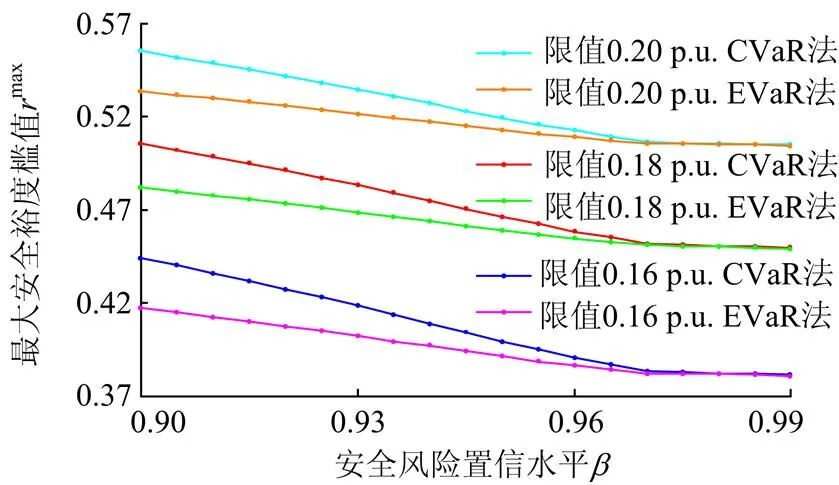
图5不同功率限值下的最大安全裕度槛值随风险置信水平变化曲线

5  结论

本文考虑了风电的不确定性对电网线路安全性的影响，建立了考虑线路安全风险约束的经济调度模型，并分别采用CVaR和EVaR方法刻画电网的安全裕度，建立了相应的电网安全风险约束，通过IEEE 30节点算例仿真，得到准确合理的调度结果，主要结论如下：

1) 针对风电的随机性，采用CVaR和EVaR方法刻画电网的安全裕度，能够量化风电的不确定性对电网安全性的影响，易于分析安全性和经济性的平衡关系，并且能够简化计算，是解决电力系统中带安全风险约束问题的一种新方法。

2) 通过数值实验，比较得出了两种安全裕度刻画方法对系统的影响。EVaR方法提供的安全性比CVaR方法提供的安全性要高，但是相应的经济费用比CVaR法要高，而且裕度槛值的范围也比CVaR法要小。同时电网的安全经济调度中存在一个最大不变的安全经济费用。

3) 适当提供网络中关键线路的功率限值，不仅能够降低电网的经济运行费用，而且可以提高全网运行的安全性。

4) 本文发展了CVaR和EVaR在电力系统中的应用，并且通过电力系统中仿真测试验证了两者的数学理论关系，是这两种风险刻画方法的新扩展，同时这两种方法可以用来解决电力系统中其它相关风险问题。

[1] 徐帆, 耿建, 姚建国, 等. 安全约束经济调度建模及应用[J]. 电网技术, 2010, 34(11): 55-58.

XU Fan, GENG Jian, YAO Jianguo, et al. Modeling and application of security constrained economic dispatch[J]. Power System Technology, 2010, 34(11): 55-58.

[2] 孙元章, 吴俊, 李国杰, 等. 基于风速预测和随机规划的含风电场电力系统动态经济调度[J]. 中国电机工程学报, 2009, 29(4): 41-47.

SUN Yuanzhang, WU Jun, LI Guojie, et al. Dynamic economic dispatch considering wind power penetration based on wind speed forecasting and stochastic programming[J]. Proceedings of the CSEE, 2009, 29(4): 41-47.

[3] 王健, 谢桦, 孙健, 等. 基于机会约束规划的主动配电网能量优化调度研究[J]. 电力系统保护与控制, 2014, 42(13): 45-52.

WANG Jian, XIE Hua, SUN Jian, et al. Study on energy dispatch strategy of active distribution network using chance-constrained programming[J]. Power System Protection and Control, 2014, 42(13): 45-52.

[4] 夏澍, 周明, 李庚银. 考虑线路安全校核的含风电电力系统有功和备用协调调度[J]. 中国电机工程学报, 2013, 33(13): 18-26.

XIA Shu, ZHOU Ming, LI Gengyin. A coordinated active power and reserve dispatch approach for wind power integrated power systems considering line security verification[J]. Proceedings of the CSEE, 2013, 33(13): 18-26.

[5] 夏澍, 周明, 李庚银. 含大规模风电场的电力系统动态经济调度[J]. 电力系统保护与控制, 2011, 39(13): 71-77.

XIA Shu, ZHOU Ming, LI Gengyin. Dynamic economic dispatch of power system containing large-scale wind farm[J]. Power System Protection and Control, 2011, 39(13): 71-77.

[6] 雷雪姣, 潘士娟, 管晓宏, 等. 考虑传输安全裕度的电力系统发电经济调度[J]. 中国电机工程学报, 2014, 34(31): 5651-5658.

LEI Xuejiao, PAN Shijuan, GUAN Xiaohong, et al. Transmission safety margin constrained unit commitment in power systems[J]. Proceedings of the CSEE, 2014, 34(31): 5651-5658.

[7] 任博强, 彭鸣鸿, 蒋传文, 等. 计及风电成本的电力系统短期经济调度建模[J]. 电力系统保护与控制, 2010, 38(14): 67-72.

REN Boqiang, PENG Minghong, JIANG Chuanwen, et al.Short-term economic dispatch of power system modeling considering the cost of wind power[J]. Power System Protection and Control, 2010, 38(14): 67-72.

[8] 罗超, 杨军, 孙元章, 等. 考虑备用容量优化分配的含风电电力系统动态经济调度[J]. 中国电机工程学报, 2014, 34(34): 6109-6118.

LUO Chao, YANG Jun, SUN Yuanzhang, et al. Dynamic economic dispatch of wind integrated power system considering optimal scheduling of reserve capacity[J]. Proceedings of the CSEE, 2014, 34(34): 6109-6118.

[9] 刘德伟, 郭剑波, 黄越辉, 等. 基于风电功率概率预测和运行风险约束的含风电场电力系统动态经济调度[J]. 中国电机工程学报, 2013, 33(16): 9-15.

LIU Dewei, GUO Jianbo, HUANG Yuehui, et al. Dynamic economic dispatch of wind integrated power system based on wind power probabilistic forecasting and operation risk constraints[J]. Proceedings of the CSEE, 2013, 33(16): 9-15.

[10]冉晓洪, 苗世洪, 刘阳升, 等. 考虑风光荷联合作用下的电力系统经济调度建模[J]. 中国电机工程学报, 2014, 34(16): 2552-2560.

RAN Xiaohong, MIAO Shihong, LIU Yangsheng, et al. Modeling of economic dispatch of power system considering joint effect of wind power, solar energy and load[J]. Proceedings of the CSEE, 2014, 34(16): 2552-2560.

[11]周任军, 姚龙华, 童小娇, 等. 采用条件风险方法的含风电系统安全经济调度[J]. 中国电机工程学报, 2012, 32(1): 56-63.

ZHOU Renjun, YAO Longhua, TONG Xiaojiao, et al. Security economic dispatch in wind power integrated systems using a conditional risk method[J]. Proceedings of the CSEE, 2012, 32(1): 56-63.

[12] URYASEV S. Conditional value-at-risk, optimization algorithms and applications[J]. Financial Engineering News, 2000, 2(3): 1-5.

[13] ROCKAFELLER T, URYASEV S. Conditional value-at- risk for general loss distributions[J]. Journal of Banking and Finance, 2002, 26(7): 1443-1471.

[14] AHMADI-JAVID A. Entropic value-at-risk: a new coherent risk measure[J]. Journal of Optimization Theory and Applications, 2012, 155(3): 1105-1123.

[15] VILLANUEVA D, PAZOS J L, FEIJOO A. Probabilistic load flow including wind power generation[J]. IEEE Transactions on Power Systems, 2011, 26(3): 1659-1667.

[16] BASU M. Economic environmental dispatch using multi- objective differential evolution[J]. Applied Soft Computing,2011, 11(2): 2845-2853.

[17]郭琳, 文旭, 赵志强, 等. 计及节能风险评估的月度随机规划调度模型[J]. 电力系统保护与控制, 2015, 43(16): 22-29.

GUO Lin, WEN Xu, ZHAO Zhiqiang, et al. A stochastic programming monthly generation dispatching model considering energy-saving risk assessment[J]. Power System Protection and Control, 2015, 43(16): 22-29.

[18]朱文昊, 谢品杰.基于CVaR的峰谷分时电价对供电公式购电组合策略影响分析[J]. 电力系统保护与控制, 2015, 43(14): 16-21.

ZHU Wenhao, XIE Pinjie. Infuluence analysis CVaR model based TOU electricity price on portfolio strategy[J]. Power System Protection and Control, 2015, 43(14): 16-21.

(编辑 张爱琴)

Power system economic dispatch under CVaR and EVaR security operation risk management

YI Guowei, TONG Xiaojiao, ZHOU Peng, ZHAI Yunfeng, YE Zhonghang

(College of Electrical and Information Engineering, Changsha University of Science and Technology, Changsha 410004, China)

For the influence of wind energy connected to the power grid on security and stability of power system, a security risk constraints economic dispatch model is established based on risk management method and random optimization modeling theory. In order to quantify and limit the impact of wind power generation randomness on the system security, this paper uses conditional value-at-risk (CVaR) and entropic value-at-risk (EVaR) to depict the security margin of power system and uses risk margin threshold value to limit the security margin as the power system security risk constraints. It uses stochastic simulation method to convert the system safety risk constraints to deterministic convex constraints. Numerical simulation of the IEEE 30 node validates the rationality of the model and the effectiveness of the method, then it contrasts the dispatch results under different safety margins and confidence levels comprehensively as well as the difference of two methods which depict the security margin risk value.

This work is supported by National Natural Science Foundation of China (No. 71371065 and No. 11171095).

conditional value-at-risk; entropic value-at-risk; security operation risk constraint; security margin; security economic dispatch

10.7667/PSPC151039

2015-06-22；

2015-09-10

易国伟(1989-)，男，通信作者，硕士研究生，研究方向为含风电电力系统经济调度；E-mail: 958212422@qq.com

童小娇(1962-)，女，博士，教授，硕士生导师，主要研究方向为优化理论与应用、电力系统分析；E-mail: tongxj@csust.edu.cn

国家自然科学基金项目(71371065, 11171095)