小学数学解题中常用的数学思维方法

江苏盐城市实验小学（224000） 姚婷婷

小学数学解题中常用的数学思维方法

江苏盐城市实验小学（224000） 姚婷婷

数学思维方法是数学思维能力的具体表现形式。引导学生运用数学思想方法分析和解决数学问题，有助于培养学生解题的灵活性、变通性以及创造性，发展学生的数学思维能力。

数学思维方法比较图解假设

综观学生的解题现状，不难发现，许多学生在解答数学问题时往往无从下手，从而产生畏难情绪，究其原因，是学生解题思想方法把握不当，解题思维僵化，思路不开阔。因此，教师要重视学生数学思维的训练，引导学生灵活巧妙地运用数学思维方法分析和解决数学问题，从而培养学生解题的灵活性、变通性以及创造性，发展学生的解题和思维能力，提高学生的解题效率。

一、巧用比较法，对比分析，把握本质

比较法，即通过对比数学问题的相同点和不同点，深入剖析产生差异的原因，从而全面深刻地认识问题的本质，探求解决问题的方法。巧用比较法进行对比分析，往往可以开拓学生思维，培养学生对比分析的思维能力。

［例1］小兰买了3支铅笔和5本数学本，用去了5.5元，小音买了同样的铅笔5支和5本数学本，用去了7.5元。求每本数学本和每支铅笔售价多少元。

解析：列表如下：

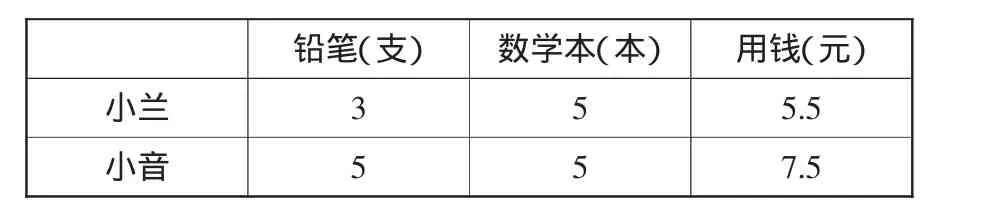
铅笔（支）　数学本（本）　用钱（元）小兰　3　5　5.5小音　5　5　7.5

比较小兰和小音两组数据可以发现，两人所买数学本相同，小音比小兰多买了（5-3）支铅笔，多用了（7.5-5.5）元，所以每支铅笔的售价应是（7.5-5.5）÷（5-3）=1.0（元），而每本数学本售价是（5.5-1.0×2）÷5=0.5（元）。

二、注重图解法，由数想图，化难为易

图解法，是指在解决某一数学问题时，通过画图的形式，将题意表达出来，然后观察分析图形，找出数量关系，从而找到解决问题的突破口。图解法是一种数形结合的思想方法，巧妙运用图解法，由数想图，往往可以达到化难为易、化繁为简、优化解题的目的。

［例2］ 一个正方形，若它的边长都增加6厘米，所得的正方形面积比原正方形的面积大216平方厘米，试求原来正方形的边长是多少厘米。

解析：该题若用一般方法进行解答，难度较大，若巧妙借助图解法，画出以下三幅图形就可以使问题得以快速解答。

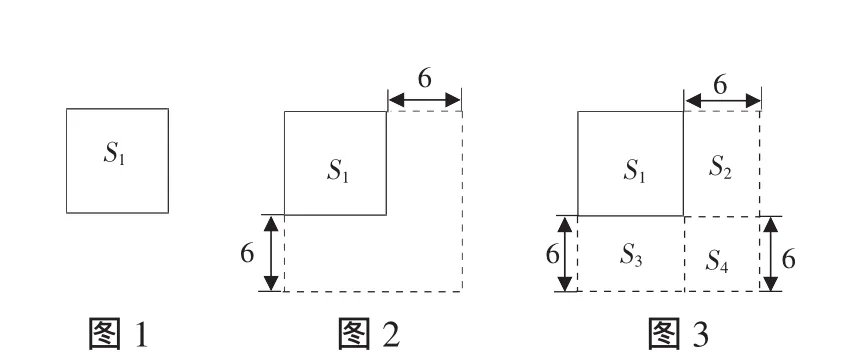
S1表示原正方形。

（1）S2+S3+S4=216（平方厘米）。

（2）S4是表示边长为6厘米的正方形，可求得面积是6×6=36（平方厘米）。

（3）S2与S3是两个等长、等宽的长方形，面积都为（216-36）÷2=90（平方厘米）。

已知其中一边宽是6厘米，就能求出另一条边的长，这两个长方形的长也就是原来正方形的边长。

列综合式得（216-36）÷2÷6=15（厘米）。

答：原来正方形的边长为15厘米。

三、尝试假设法，猜想推测，优化思路

假设法是数学解题中较为常用的一种推测性数学思想方法，主要通过假设问题中的某些数量相等或未知量为已知数量，使复杂问题简单化，进而猜想推测一些关系和结论，快速有效地解决问题。巧妙地运用假设法进行解题，往往可以使问题中的隐蔽条件清晰化，复杂的数学关系简单明朗化，从而快速找到最佳解题之道。

［例3］ 甲乙两人同时从相距44千米的A地向B地行驶，甲骑自行车每小时行16千米，乙步行每小时行8千米。甲到B地后休息2小时后返回A地，中途与乙相遇，相遇时乙行驶了多少千米？

解析：假设甲到B地后没有休息，继续行驶，那么相遇时甲乙两人共行的路程是44×2+16×2=120（千米）。由此可求出两人经过多长时间相遇，即乙行驶的时间为120÷（16+8）=5（小时），所以相遇时乙行驶了8×5=40（千米）。

总之，教师要立足实际，结合典型例题，加以巧妙引导，以帮助学生正确理解、掌握和运用数学思维方法，从而提升学生的数学解题能力，培养学生良好的思维品质，促进学生有效学习。

（责编童夏）

G623.5

A

1007-9068（2016）26-044