小议高中数学中的一题多解

张 轩

（河北衡水第一中学）

小议高中数学中的一题多解

张 轩

（河北衡水第一中学）

在考试中，同学们看到一道数学题，总想用最简捷的办法来解出来 。通过多年的学习经验,其实我认为，第一思路就是最好的思路。因为考试过程中没有太多的时间去尝试，所以怎样形成自己的第一思路，这就需要我们在平时的练习中注意一题多解的问题，并且形成对某一类问题最佳（适合自己）的第一思路。下面就以一道例题为例，浅谈一题多解的问题。

已知 x²＋y²＝1 m²＋n²＝3， 求 mx+ny 的最大值

思路一：遇到两数的平方和等于常数的问题。可选用三角换元，从而由三角函数得到最大值

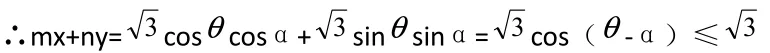
当cos（-α）=1时，取得最大值3

思路二：向量法

解：设P（x,y） Q(m,n)

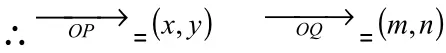
思路三：放缩法

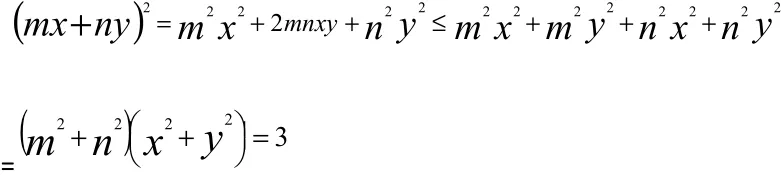
当且仅当my=nx时，取“=”

思路四：柯西不等式

∴mx+ny的最大值为3

通过上述这个例题，我认为遇到这一类题，选用思路一最佳。

其原因如下：思路四看似简单，但是在高中学习中是选修内容，在平时的做题过程很少用到，容易遗忘；思路三是借助的基本不等式进行放缩，但是放缩的方向不易寻找；思路二是与向量联系，必须能够由mx+ny想到一个向量的数量积；而思路一借助于三角换元，而三角换元是高考中，必考的内容。我们能够很容易的联想到。因此我自己遇到这一类题就选择思路一。

针对以上的分析，我自己认为，只有在平时练习时总结出自己某一类问题的第一思路，才能够在考试中能得到最好的发挥，即通题法。但是在平时的练习中注意一题多解问题，既可以让我们把握知识间的联系，也能够让我们在考试中能够产生“灵感”。灵感的产生就是源于平时的多思、多想、多总结。

以上是我对一题多解的一点小小的见解，也许有不当之处，望给予指正。