高中物理电磁问题的微观解析研究

李钰冰 指导教师：王建秋

（河北省唐山市第二中学高三（5）班 063000）

高中物理电磁问题的微观解析研究

李钰冰 指导教师：王建秋

（河北省唐山市第二中学高三（5）班 063000）

本文从几个典型的物理模型入手，研究了高中物理电磁问题在宏观处理困难时采用微观处理的简便性。应用微积分理论计算方法，思路清晰，可以使得题目计算简单明了。

电磁场；微积分；宏观；微观

一、简单问题宏观与微观处理对比分析

例1、在磁感应强度为B、方向垂直直面向里的均匀磁场中，一根长度为L的导体细棒，以角速度ω绕细棒的一端a做匀速运动，求导体细棒在两端的感应电动势。

解：宏观处理：

微观处理：

从微元角度考虑，导体棒是由无数个小段dL组成的，dL在磁场中做切割磁感线运动产生电动势，dE=Bv×dL ；v=ωL；所以dE=Bω L× dL ；

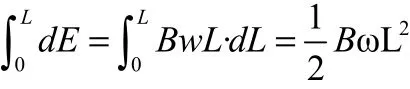
我们看到微观处理实际上就是把研究对象中的一个很小很小可以表征其运动规律的“元”提取出来，避开宏观处理时的困难之处，然后再推导到宏观。这实际上就是高等数学中先微分再积分的过程。

二、复杂问题的微观处理

例2、在矩形导线框的平面有磁感应强度为B、垂直平面向里的均匀磁场，在矩形导线框上有一质量为m，长为L的可移动导体细棒ab，矩形导线框上有一阻值为R的电阻，矩形导线框阻值不计。某一时刻，导体棒以速度v0向右运动，求导体棒的速度v随时间变化的函数。

分析：我们处理的变速问题一般都是加速度不变，然而本题中运动的导体棒切割磁感线产生感应电流，感应电流在磁场中受安培力，合力变化继而加速度变化，以宏观角度很难得到v随时间变化的关系，接下来我们尝试从微观角度处理该问题。

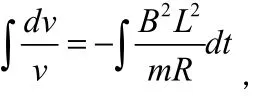
例3、有一个闭合线圈，一段直线一段弧线，通有电流I，置于均匀磁场B中，线圈平面与B垂直。求整个回路所受磁场力。

分析：对于直线部分我们很容易求解，但是对于弧线就不好解决了，可以猜想由于弧线电流方向与直线电流方向相反，由安培定律可知两者安培力方向相反，大小可能相等，整体回路所受安培力为零。但是我们需要用数学工具进行推导验证，确定猜想成立。

解：由安培定律，直线段所受安培力1F=IBab，方向为沿y轴负向。

弧线段bca可分解为无数个小段dL，其上的电流为电流元IdL，所受安培力为dF2=IBdL，方向沿径向向外，由于左半段弧与右半段弧的对称性，弧bca所受安培力在x轴方向的分量抵消。

经验总结：在匀强磁场中任意形状的闭合载流线圈所受合力皆为零。

结语：

我们知道物质是由很小的分子构成，每一个物理现象实际上都是无数个分子现象的整体表现。我们在应用中都是处理宏观问题，在处理过程中有时以宏观视角处理简便，有时以微观视角分析再推导到宏观更为容易，而且后种方式更利于了解现象本质。