一题多解示例

赵 茁

（河北衡水第一中学）

一题多解示例

赵 茁

（河北衡水第一中学）

1.已知O、A、B、C为同一直线上的四点、AB间的距离为l1,BC间的距离为l2,一物体自O点由静止出发，沿此直线做匀速运动，依次经过A、B、C三点，已知物体通过AB段与BC段所用的时间相等。求O与A的距离.

解法一

设物体加速度为a， 到达A点的速度为vA，通过AB 段和BC段所用的时间为t, 则有：

联立（1）（2）式得

O 与A 的距离为 l

解法二

联立（1）（2）式得

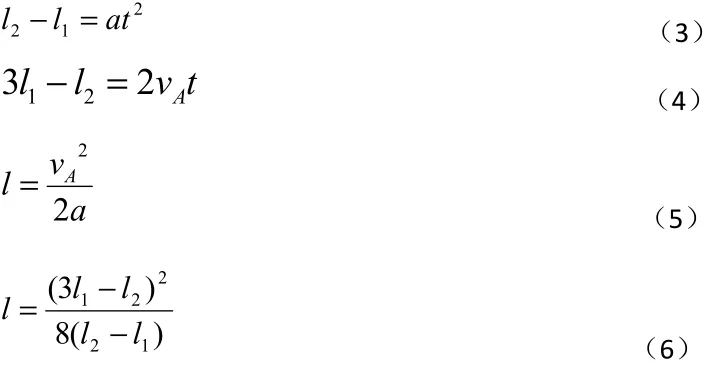
解法三

联立（1）（2）式得

解法四 （由距离公式计算）

由O 到A 距离为 l， 时间t1, 通过AB 段和BC段所用的时间为

联立（1）（2）（3）式得

解法五（利用平均速度计算）

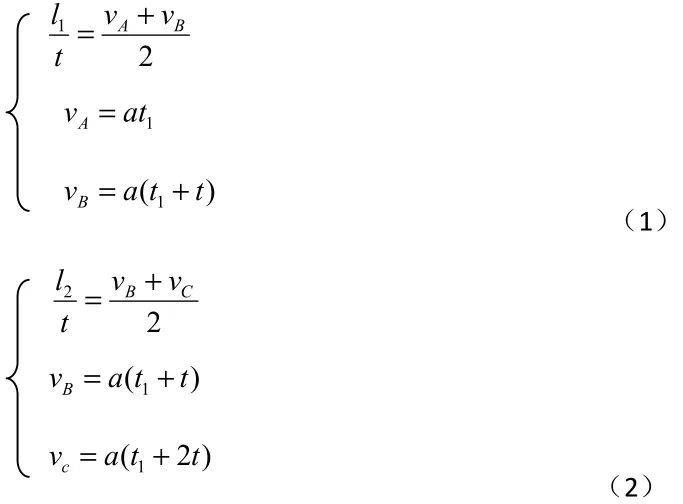
联立（1）（2）式得

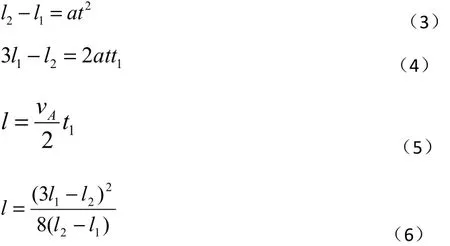
解法六

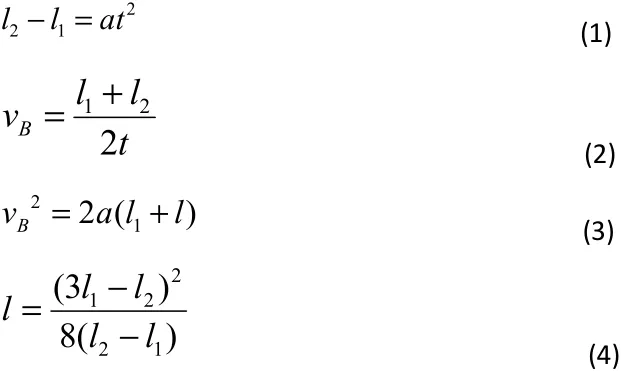
2． 天空有近似等高的浓云层，为了测量云层的高度，在水平地面上与观测者的距离为d＝3.0km处进行一次爆炸，观测者听到由空气直接传来的爆炸声和由云层反射来的爆炸声时间上相差△t＝6.0s。试估算云层下表面的高度。已知空气中的

方法一：

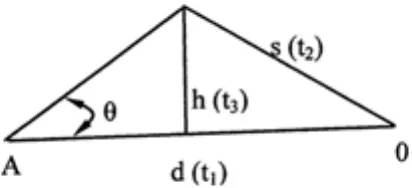
用t1表示爆炸声从A直接传到O处所经时间，有：d=vt1 ①

用t2表示爆炸声从A经云层反射到达O处所经时间，因为入射角等于反射角，有：

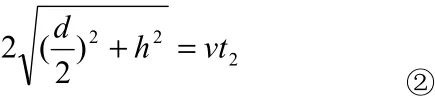
得：h=2.0×103m（或h=2.0km） ⑤

方法二：

方法三：

方法四：

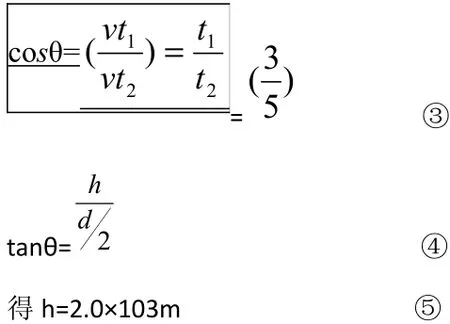
方法五：

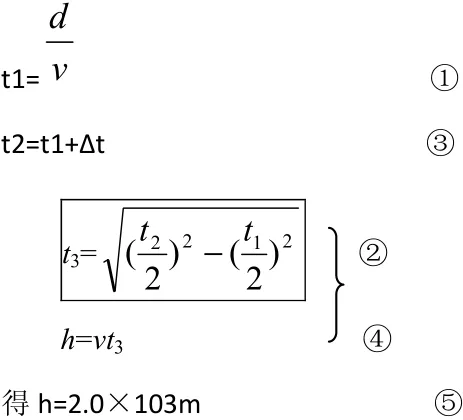
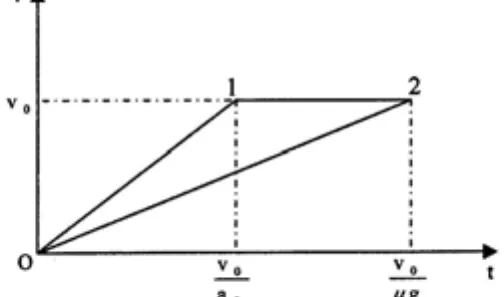
3．一水平的浅色长传送带上放置一煤块（可视为质点），煤块与传送带之间的动摩擦因数为。起始时，传送带与煤块都是静止的。现让传送带以恒定的加速度a0开始运动，当其速度达到v0后，便以此速度匀速运动。经过一段时间，煤块在传送带上留下了一段黑色痕迹后，煤块相对于传送带不再滑动。求此黑色痕迹的长度。

解法2：

坐标值如果是用其他符号表示，必须有相应的公式支持才能得分。

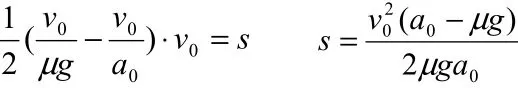
解法3：

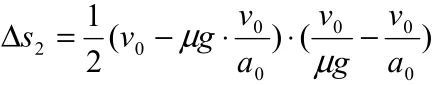
总的相对位移

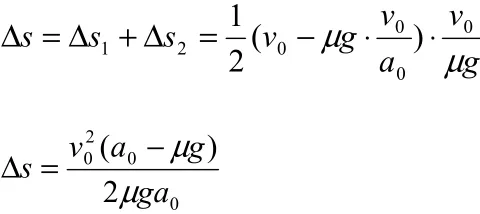
解法4：

对煤块：a=g，mg(t1+t2)=mv0

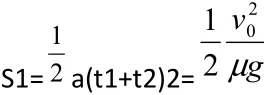
传送带：v0=a0t1

煤块相对于传送带的位移为：

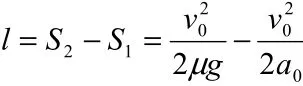
解法5：

解法6：

第一阶段相对位移

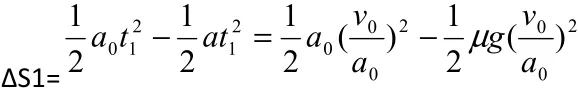
第二阶段相对位移：

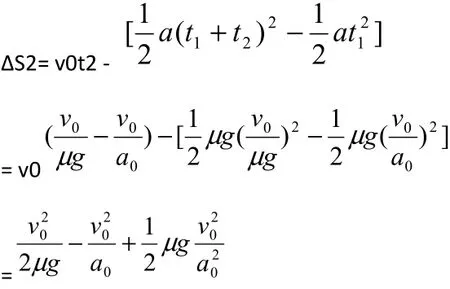
总相对位移：

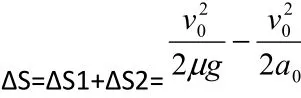
4．甲、乙两运动员在训练交接棒的过程中发现：甲经短距离加速后能保持9m/s的速度跑完全程；乙从起跑后到接棒前的运动是匀加速的。为了确定乙起跑的时机，需在接力区前适当的位置设置标记。在某次练习中，甲在接力区前S0=13.5m处作了标记，并以V=9m/s的速度跑到此标记时向乙发出起跑口令。乙在接力区的前端听到口令时起跑，并恰好在速度达到与甲相同时被甲追上，完成交接棒。已知接力区的长度为L=20m。

求：（1）此次练习中乙在接棒前的加速度a；

（2）在完成交接棒时乙离接力区末端的距离。

方法一：利用运动学公式

（1）求乙在接棒前的加速度a：

甲发出口令后，至甲乙达到共同速度这段时间内，对乙列方程：

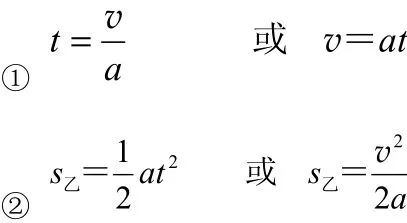
对甲列方程：

③ s甲＝vt

甲乙二人位移关系为：

④ s甲＝s乙＋s0或s甲＝s乙＋13.5

联立①—④式，得

⑤ a=3m/ s2

（2）求完成交接棒时，乙与接力区末端的距离：

这段时间内，乙在接力区的位移为：

⑥ s乙＝13.5m

完成交接棒时，乙与接力区末端的距离为：

⑦ d=6.5m

方法二：利用平均速度

（1）求乙在接棒前的加速度a：

甲发出口令后，至甲乙达到共同速度这段时间内，对乙列方程：

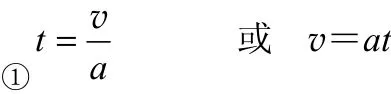
对甲列方程：

③—④ s乙＋s0=vt 或s乙＋13.5=vt

联立①—④式，得

⑤ a=3m/ s2

（2）求完成交接棒时，乙与接力区末端的距离：

这段时间内，乙在接力区的位移为：

⑥s乙＝13.5m

完成交接棒时，乙与接力区末端的距离为：

⑦d=6.5m

方法三：利用速度-时间图像+运动学公式

由于甲为匀速运动，乙为匀加速运动，交接棒时甲追上乙，并且甲乙速度相等，据此可画出速度—时间图像如下：

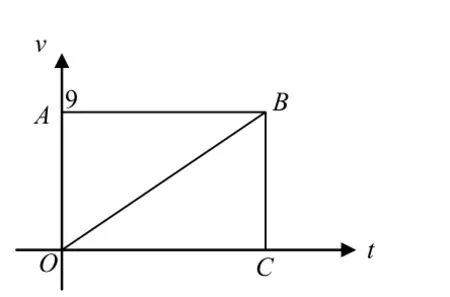
交接棒时，甲的总位移为矩形OABC的面积，乙的位移为三角形OBC的面积。图中三角形 OAB的面积为甲比乙多行的位移。由题可知，三角形 OAB的面积为13.5m。

由几何学知识可知，三角形OBC的面积与三角形OAB的面积相等，故有：

①（相当于方法I或II中的⑥式） s乙＝13.5m

② （相当于方法I或II中的①—④式）由运动学公式，知：

③ （相当于方法I或II中的⑤式） 由此可得：a=3m/ s2

④ （相当于方法I或II中的⑦式） 完成交接棒时，乙与接力区末端的距离为：

d=6.5m