有限长半充液圆柱壳振动特性分析

李天匀，王露，郭文杰，杨国栋，朱翔

华中科技大学船舶与海洋工程学院，湖北武汉430074

有限长半充液圆柱壳振动特性分析

李天匀，王露，郭文杰，杨国栋，朱翔

华中科技大学船舶与海洋工程学院，湖北武汉430074

基于能量泛函变分原理，研究有限长半充液圆柱壳自由振动特性和受迫振动特性。壳体各向位移采用三角级数与傅立叶级数的组合形式，利用三角级数与傅立叶级数的正交性，在变分后可消去其他2个方向的位移，只保留径向位移。通过对固液耦合接触面连续条件的正交化处理以及自由液面边界条件，可建立流体载荷幅值与径向位移幅值的关系，最终得到流固耦合控制方程。结果对比表明，能量泛函变分方法正确、有效，可为求解半充液圆柱壳固液耦合振动问题提供新的思路。

能量泛函变分；圆柱壳；振动特性；正交性

网络出版地址：http://www.cnki.net/kcms/detail/42.1755.TJ.20160317.1056.028.html期刊网址：www.ship-research.com

引用格式：李天匀，王露，郭文杰，等.有限长半充液圆柱壳振动特性分析［J］.中国舰船研究，2016，11（2）：106-110.

LI Tianyun，WANG Lu，GUO Wenjie，et al.Vibration characteristics analysis of finite cylindrical shells semi-filled

with liquid［J］.Chinese Journal of Ship Research，2016，11（2）：106-110.

0　引　言

圆柱壳结构在船舶工程中应用十分广泛，例如，水下潜艇就可以近似等效为浸没圆柱壳结构，可以将各类船舶管路看成充液圆柱壳结构。通常，都是在无限域中研究此类结构，但在许多工况下，结构往往处于部分充液或部分浸没情况，比如，在码头系泊情况下的潜艇，或者部分充液的管路。因此，研究此类工况下结构固液耦合振动特性就显得尤为重要。

国内外大量的学者曾做过有关全充液（浸没）圆柱壳的研究工作。Lee和Lu［1］以有限长简支充液圆柱壳为研究对象，提出了求解固有频率的一种简便算法。Zhang等［2］运用波传播法分析了充液圆柱壳的自由振动特性。Liu等［3］研究了静水压力下圆柱壳的声辐射特性。陈忱等［4-5］提出了水下圆柱壳的临界载荷预报方法。

而有关部分充液（浸没）圆柱壳的研究工作则较少。Selmane和Lakis［6］研究了圆柱壳部分充液时的自振特性，但并未计及自由液面的影响。王斌和汤谓霖［7］研究了半潜状态无限长圆柱壳的声辐射特性。叶文兵等［8-9］基于波传播方法，对潜浮状态下的无限长圆柱壳声振特性进行了研究，得出高频激励时远场声压近似于解析表达式。Amabili［10-11］基于瑞利—李兹法，求解了部分充液圆柱壳的固有频率和模态振型。Ergin等［12］利用镜像原理，结合边界元处理半无限域流体，对部分充液圆柱壳自振特性展开了分析。

本文将基于能量泛函变分原理，分析有限长半充液简支圆柱壳的振动特性。由于部分充液情况下的流体载荷解析表达式不易得到，故本文拟从特例出发来研究半充液情况，此时的流体载荷解析表达式就较易得到。利用结构和流体交界处速度连续条件，可以采用位移幅值表示流体载荷，根据三角级数和傅立叶级数的正交性最终得到总能量的简易表达式。最后，根据变分后三向幅值之间的线性关系，将控制方程简化为只与径向幅值相关的矩阵形式，以使求解受迫响应更为简便。

1　理论分析

半充液圆柱壳的长度为L，厚度为h，半径为R，周向角为θ，壳体两端简支，处于半充液状态。轴向x、周向θ和径向r的位移分别为u，v，w，点谐激励力为 fr，如图1所示。

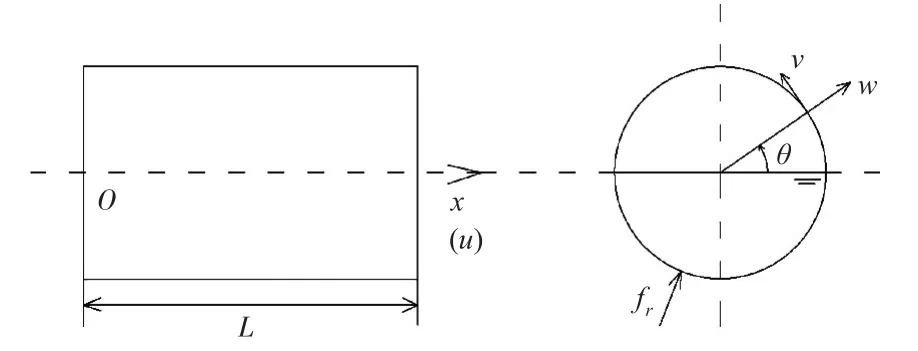
图1　半充液圆柱壳模型图Fig.1　Cylindrical shells model semi-filled with liquid

由于壳体两端简支，位移场如下所示：

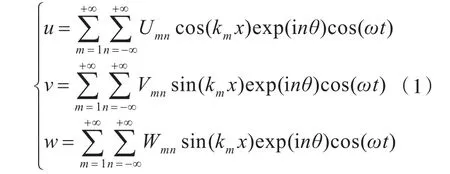
式中：m和n分别为轴向、周向波数；km=mπx/L；Umn，Vmn和Wmn分别为轴向、周向、径向位移幅值。

本文采用能量变分的方法研究有限长半充液圆柱壳的振动特性，首先，需得到各能量分量的表达式。壳体势能可以表示为

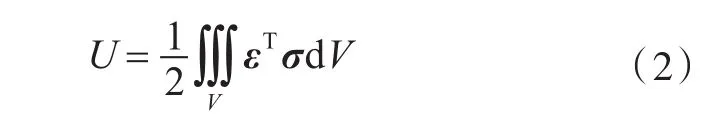
式中：ε为应变分量；σ为应力分量；V为体积。

根据正交性，也可以写成

式中：ξmn=｛Umn，Vmn，Wmn｝；Kmn为三阶Hermite矩阵。

壳体动能为

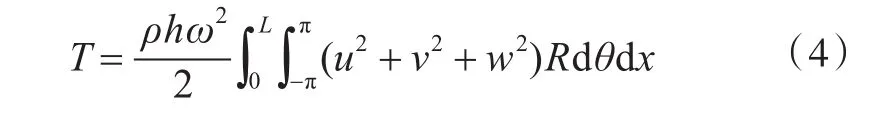
式中：ρ为结构密度；ω为角频率。

同理，根据正交性，上式可以表示为

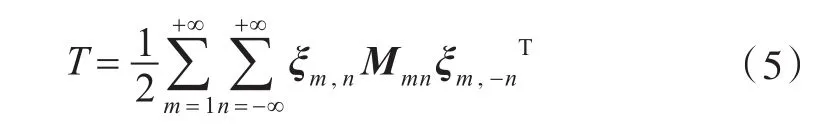
式中，Mmn为三阶对角矩阵。

流体做功为

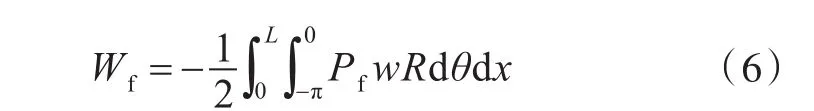
式中，Pf为结构表面流体载荷，分布区域位于角度-π～0处。

点激励力做功为

式中，F0为激励力幅值，其激励力位置位于（x0，θ0）处，激励力频率为 f0。

由上述各能量分量，可得到能量泛函表达式

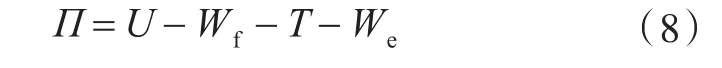
在流固耦合的求解过程中，通常是将液体看作不可压缩的理想流体。由此，可以引入速度势函数ϕ（x，r，θ，t），柱坐标系下流体的拉普拉斯方程为

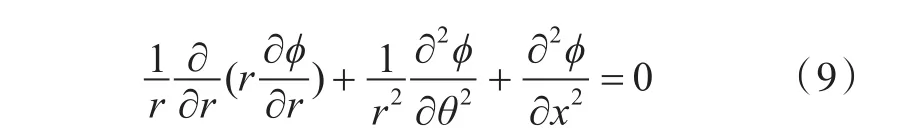
这里采用分离变量法求解拉普拉斯方程，考虑自由液面速度势为0：

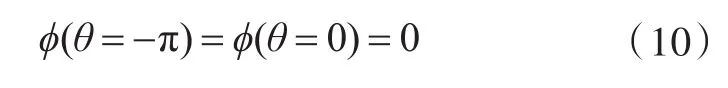
对于充液圆柱壳，满足在轴心处径向位移为0：

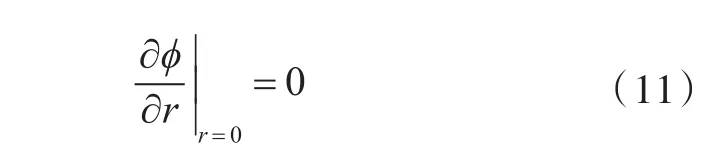
满足条件的速度势函数的表达式为

式中，Ik（）为第1类修正贝塞尔函数。

在流体与壳体的接触面上，流体的径向位移必须等于壳体的径向位移，即

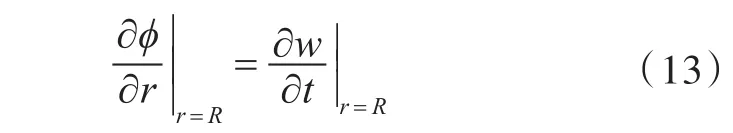
经正交化处理，得

由伯努利方程，可得壁面处的流体动压力为

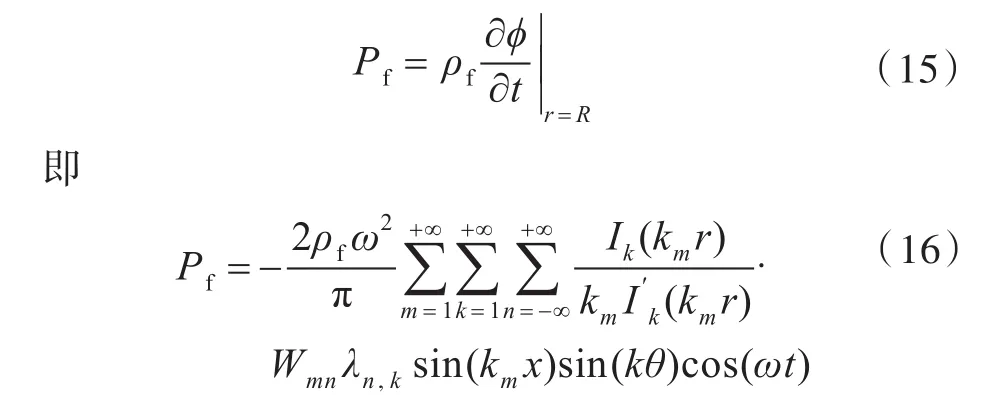
根据变分原理，满足

由对幅值Umn，Vmn的偏导为0，可以得到其与幅值Wmn的线性关系，简写为

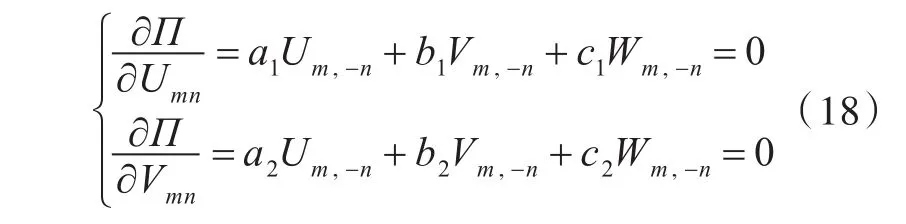
式中，a1，b1，c1和a2，b2，c2均为关于角频率ω、刚度矩阵Kmn和质量矩阵Mmn的系数，即Umn和Vmn可以由Wmn进行代换，最终根据对幅值Wmn的偏导为0，可以得到方程

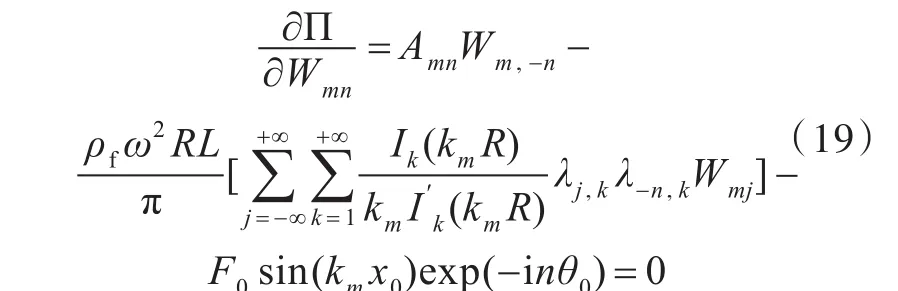
式中，Amn为关于角频率ω、刚度矩阵Kmn和质量矩阵Mmn的系数。

当n的截断数为-N～N，m的截断数为M，k的截断数为K时，上式可以写成矩阵形式，给定某一m值，方程可简写为

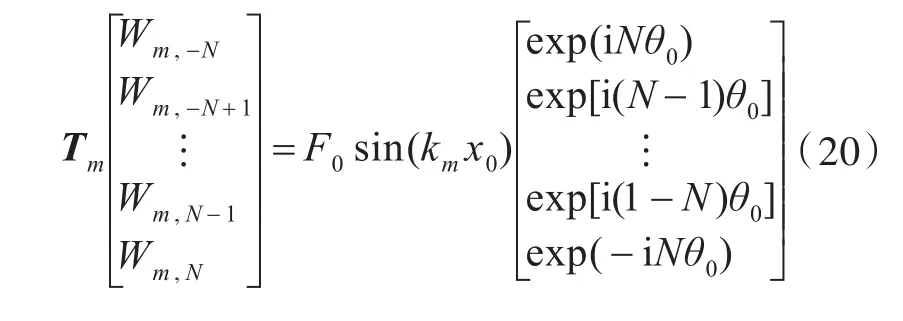
式中，Tm为2N+1阶方阵。当激励力频率 f0给定时，将Tm矩阵中的所有ω替换为2πf0便可求出Wmn；当求解自由振动时，可令Tm的行列式为0，以解得各阶固有频率。

2　数值计算

2.1半充液圆柱壳自由振动分析

模型参数取自文献［10］：壳长L=0.664 m，半径R=0.175 m，厚度h=0.001 m，壳体密度 ρ= 7 680 kg/m3，杨氏模量E=206 GPa，泊松比μ=0.3，流体密度 ρf=1 000 kg/m3。因采用本文的方法固有频率收敛较快，故取截断项数N=10，K=10；在固有频率已收敛，m=1时，取前4阶固有频率，数值仿真采用有限元软件Patran。频率及周向振型如表1和表2所示。

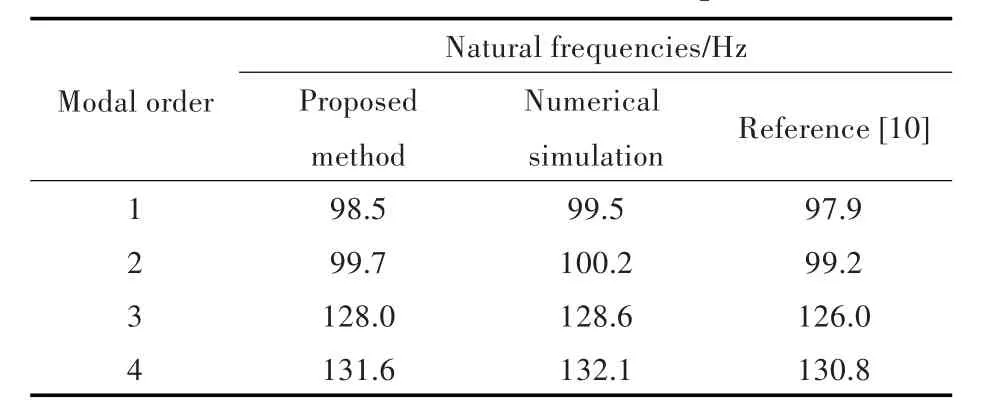
表1　前4阶固有频率Tab.1　First four order natural frequencies

表2　理论与数值仿真振型对比Tab.2　Comparison of vibration modes between theoretical method and numerical simulation

由表1和表2可以看出，采用本文方法计算自由振动固有频率准确、有效。相对于全浸没（充液）或者真空中的情况，从振型可以看出，并没有出现规则的周向波，实际上，每一阶模态振型都是由许多规则周向波按一定权重进行的叠加，这是区别于全浸没（充液）圆柱壳或者光壳的地方。

2.2半充液圆柱壳受迫振动分析

模型保持不变，点激励力幅值 F0=1，位于x0=L/2，θ0=-π/2处，激励力频率范围为2～200 Hz，扫频间隔为2 Hz。在壳体表面取4个测点，点1的坐标x1=L/2，θ1=-π/2；点2的坐标 x2=L/2，θ2=0；点3的坐标x3=L/4，θ3=-π/2；点4的坐标x4=L/4，θ4=0。定义位移响应级LW=20 log10（wa/w0），其中wa为测点径向位移绝对值，w0=10-12m。计算程序取截断项数N=10，K=10，M=8，此时，位移响应级收敛较好。由此，可以得到本文理论方法和数值仿真的测点位移响应级，如图2所示。

由图2可以明显看出，采用本文方法所得结果与数值仿真软件计算的各点位移响应级吻合较好，表明采用本文方法计算受迫响应正确、可行。同时还可看到，4个峰值点均位于100，130和 180 Hz附近，这些频率均为结构的前几阶固有频率，当激励力频率在此附近时，会引起结构共振，位移出现峰值。

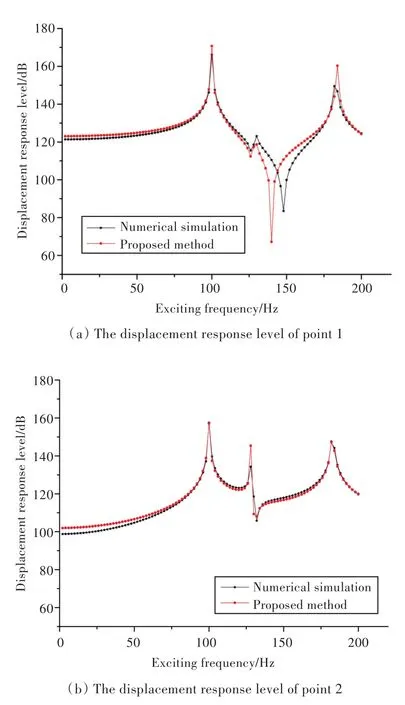
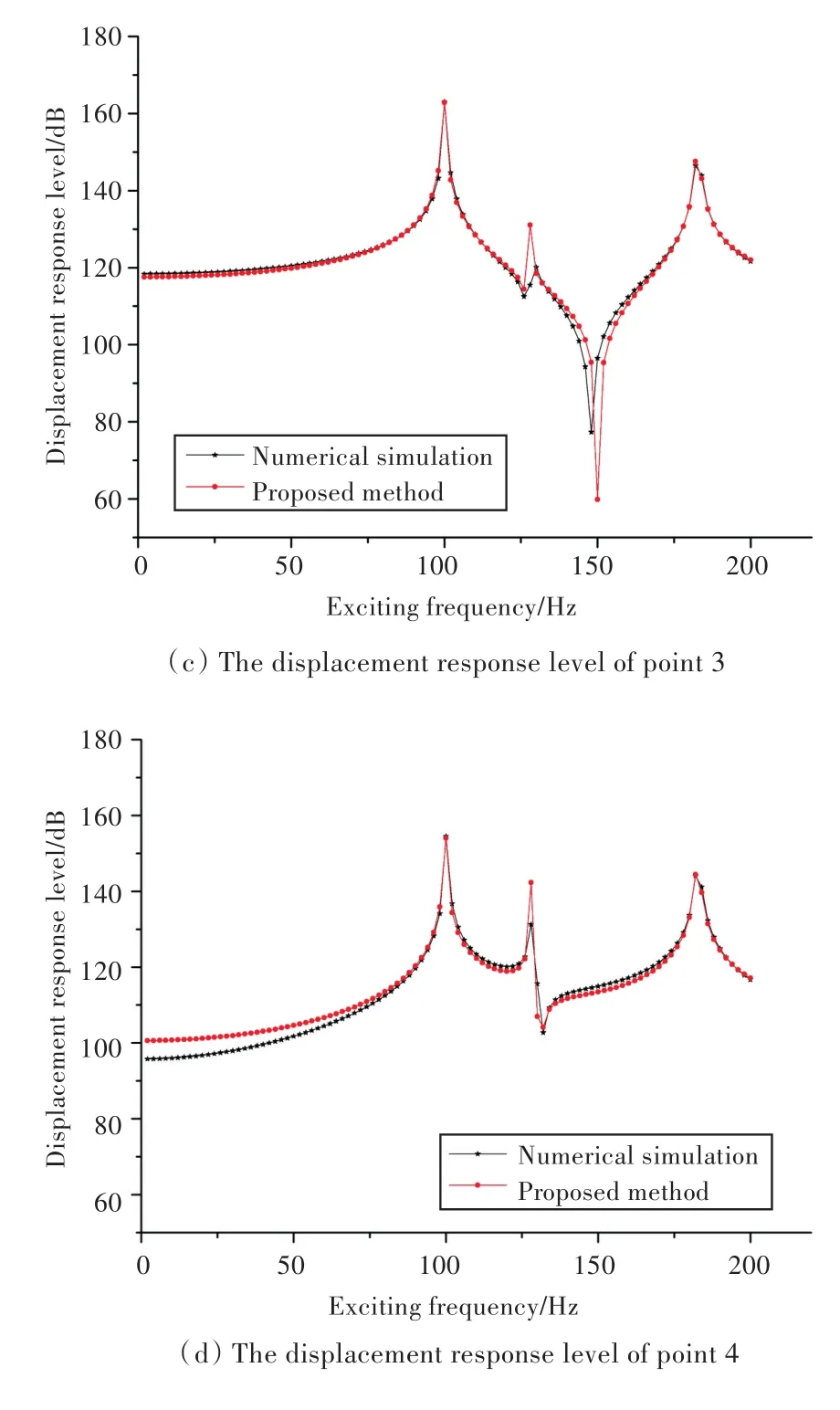
图2　各点位移响应级Fig.2　The displacement response level of each point

3　结　论

本文基于能量泛函变分原理，分析了有限长半充液简支圆柱壳的自由振动和受迫振动特性，得到以下几点结论：

1）相比于全充液或者不充液的情况，半充液简支圆柱壳的周向会产生不规则波，而非规则的周向波，这是因为部分存在的流体会引起周向模态的交互耦合，从而产生不规则的叠加波。

2）本文的位移在周向采用的是傅立叶复指数级数的展开形式，相比于傅立叶三角级数，这样可以避免因既有正弦又有余弦而带来积分方面形式的不统一，刚度矩阵和质量矩阵处理起来也更为便捷。

3）本文基于级数正交性，将三向位移幅值变换成径向位移幅值简化了算法，取得了较好的效果。

本文从部分充液的特例，即半充液情况出发，研究了圆柱壳的流固耦合振动特性。今后，还将就部分充液（浸没）情况开展更为深入的研究。

［1］LEE L T，LU J C.Free vibration of cylindrical shells filled with liquid［J］.Computer&Structures，1995，54 （5）：997-1001.

［2］ZHANG X M，LIU G R，LAM K Y.Coupled vibration analysis of fluid-filled cylindrical shells using the wave propagation approach［J］.Applied Acoustics，2001，62（3）：229-243.

［3］LIU Z Z，LI T Y，ZHU X，et al.The effect of hydrostatic pressure fields on the dispersion characteristics of flu⁃id-shell coupled system［J］.Journal of Marine Science and Application，2010，9（2）：129-136.

［4］ 陈忱，李天匀，朱翔，等.基于波传播法的水下圆柱壳临界载荷-频率特性分析［J］.中国造船，2012，53 （1）：130-136. CHEN Chen，LI Tianyun，ZHU Xiang，et al.Frequency characteristics analysis for critical load of a submerged cylindrical shell based on wave propagation approach ［J］.Shipbuilding of China，2012，53（1）：130-136.

［5］ 陈忱，李天匀，朱翔，等.水下环肋圆柱壳弹性失稳临界载荷无损预报方法［J］.海洋工程，2014，32（4）：89-95. CHEN Chen，LI Tianyun，ZHU Xiang，et al.Elastic critical pressure prediction of submerged ring-stiff⁃ened cylindrical shell based on frequency characteris⁃tics analysis［J］.The Ocean Engineering，2014，32（4）：89-95.

［6］SELMANE A，LAKIS A A.Vibration analysis of aniso⁃tropic open cylindrical shells subjected to a flowing flu⁃id［J］.Journal of Fluids and Structures，1997，11（1）：111-134.

［7］ 王斌，汤谓霖.半潜状态圆柱壳振动声辐射特性研究［C］//第十二届船舶水下噪声学术讨论会.北京：中国造船工程学会，2009：33-37.

［8］叶文兵.潜浮状态下圆柱壳结构的声振特性研究［D］.武汉：华中科技大学，2012. YE Wenbing.The vibro-acoustic characteristics of cy⁃lindrical shells in the state of immersion and floating ［D］.Wuhan：Huazhong University of Technology，2009.

［9］YE W B，LI T Y，ZHU X.The vibro-acoustic character⁃istics of the cylindrical shell partially submerged in the fluid［J］.Applied Mechanics and Materials，2012（170/ 171/172/173）：2303-2311.

［10］AMABILI M.Free vibration of partially filled，hori⁃zontal cylindrical shells［J］.Journal of Sound and Vi⁃bration，1996，191（5）：757-780.

［11］AMABILI M.Flexural vibration of cylindrical shells partially coupled with external and internal fluids［J］. Journal of Vibration and Acoustics，1997，119（3）：476-484.

［12］ERGIN A，TENAREL P.Free vibration of a partially liquid-filled and submerged，horizontal cylindrical shell［J］.Journal of Sound and Vibration，2002，254 （5）：951-965.

Vibration characteristics analysis of finite cylindrical shells semi-filled with liquid

LI Tianyun，WANG Lu，GUO Wenjie，YANG Guodong，ZHU Xiang
School of Naval Architecture and Ocean Engineering，Huazhong University of Science and Technology，Wuhan 430074，China

Free vibration and forced vibration characteristics of finite cylindrical shells semi⁃filled with liq⁃uid are studied in this paper，based on the energy functional variational principle.The combined form of the triangular series and the Fourier series is used to represent the displacement of the cylindrical shell，and the orthogonality is then used to eliminate the displacement on the other two directions after the varia⁃tion，where only the radial displacement is kept.The relationship between the amplitudes of fluid load and the amplitudes of the radial displacement is established with the orthogonal processing of the continuous conditions of the solid-liquid coupling contact surface and the boundary conditions of the free liquid sur⁃face.Finally，the fluid structure coupling control equation is obtained.The results show that the proposed method is both correct and effective；in addition，it provides a new thought for solving similar problems.

energy functional variation；cylindrical shells；vibration characteristics；orthogonality

U661.44

A

10.3969/j.issn.1673-3185.2016.02.014

2015-05-29网络出版时间：2016-3-17 10:56

国家自然科学基金资助项目（51379083）

李天匀（通信作者），男，1969年生，博士，教授。研究方向：船舶结构振动与噪声控制。

E-mail：ltyz801@hust.edu.cn

朱翔，男，1980年生，博士，副教授。研究方向：船舶与海洋工程结构力学，振动与噪声控制。

E-mail：zhuxiang@hust.edu.cn