破损舰船瘫船状态倾覆概率评估方法

吕振望，马坤，李新萌

1大连理工大学运载工程与力学学部船舶工程学院，辽宁大连116024

2工业装备结构分析国家重点实验室，辽宁大连116024

破损舰船瘫船状态倾覆概率评估方法

吕振望1，2，马坤1，2，李新萌1，2

1大连理工大学运载工程与力学学部船舶工程学院，辽宁大连116024

2工业装备结构分析国家重点实验室，辽宁大连116024

国际海事组织已基本确定了完整船瘫船状态下的第2层薄弱性倾覆概率评估方法。由于破损舰船在风浪中运动的复杂性，破损舰船瘫船状态下的倾覆概率评估方法还未提出。基于完整船瘫船失效模式评估方法的思想，对破损舰船的横摇运动进行简化，提出一种评价破损舰船瘫船状态下倾覆概率的方法，并利用实船进行计算分析。分析各参数对倾覆概率的影响，研究对称进水和非对称进水这2种情况下的倾覆概率。结果表明：所提的用于评价破损舰船瘫船状态下倾覆概率的方法可行，其中非对称进水更为危险，可为研究破损舰船瘫船稳性提供参考。

破损舰船；瘫船状态；倾覆概率；破损稳性

网络出版地址：http://www.cnki.net/kcms/detail/42.1755.TJ.20160317.1056.008.html期刊网址：www.ship-research.com

引用格式：吕振望，马坤，李新萌.破损舰船瘫船状态倾覆概率评估方法［J］.中国舰船研究，2016，11（2）：21-26.

LV Zhenwang，MA Kun，LI Xinmeng.Vulnerability assessment for dead-ship stability failure mode of the damaged warship［J］.Chinese Journal of Ship Research，2016，11（2）：21-26.

0　引　言

船舶稳性规范是船舶设计的指导性文件。第1代完整稳性规则，即《2008年国际完整稳性规则》（2008 IS Code）［1-2］现已开始执行，但该规则主要是基于经验，不足以防止因动态稳性而导致的舰船倾覆的发生［3］。因此，国际海事组织（IMO）启动了第2代完整稳性衡准的制定工作。完整舰船瘫船稳性作为其中的失效模式之一，是当今稳性研究的热点，并正在被逐步完善。

目前，不少学者和科研机构对完整舰船瘫船稳性进行研究并取得了丰硕的成果。2004年，Bulian和Francescutto［4］提出了风浪联合作用下瘫船倾覆概率的数学预报方法。王田华等［5-6］建立了内倾船型在横浪中的横摇运动数学模型，并结合试验进行了验证。曾柯等［7］根据第2代完整稳性衡准草案分析了不同复原力臂曲线拟合方法及有效波陡的计算方法对倾覆概率的影响，并对瘫船稳性提出了修改意见。

以上方法均是基于完整舰船来对其瘫船稳性进行的计算，对破损舰船瘫船状态下的倾覆概率评估还未见有公开发表的文献。本文将基于第2代完整稳性衡准草案中瘫船稳性评估方法的思想，将其扩展到舰船在某一破损状态下倾覆概率的评估中，并将评估过程中破损舱内的进水视为船上的液体载荷，利用增加重量法，通过反复迭代求出破损舰船进水最终平衡位置的浮态和稳性参数，建立破损舰船单自由度横摇运动方程，计算不规则横风和横浪作用下的倾覆概率，并通过实船计算验证该方法的可行性。

1　某一破损状态下倾覆概率评估方法

要评估破损舰船瘫船状态在风浪中的失效模式，就需要建立破损舰船的横摇运动模型。但横摇运动十分复杂，尤其是在进水过程中，涉及到舱内水的晃荡、舱内进水速度和船舶运动的耦合作用。因此，在时域内对破损舰船的横摇运动进行模拟十分困难。为此，本文进行如下简化：

1）本文的计算在2014 SDC1会议假定的基本条件上进行［8］，主要假定条件如下：

（1）假定舰船为在特定暴露时间下处于不规则波和阵风环境条件下的瘫船；

（2）风和浪假定同向传播，水深假定为无限水深；

（3）舰船假定处于横风横浪中。

2）在计算倾覆概率的过程中，需要计算舰船破损后的横摇角，而大量的时域模拟表明，进水阶段对破损舰船的横摇角幅值影响较小［9-11］，故本文在计算过程中不考虑进水过程的影响，即从破损后达到静平衡角时开始计算（此时类似于载有液体载荷的完整船舶，可采用计算完好油船倾覆概率的方法进行计算）。

3）在舰船横摇过程中，不考虑水的进出问题。

1.1单自由度横摇运动方程

破损舰船在不规则横风横浪作用下的单自由度非线性横摇运动物理模型按下式建立：

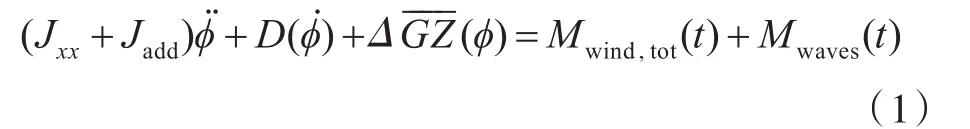
式中：Jxx为破损舰船的横摇惯性矩；Jadd为破损舰船随时间变化的横摇附加惯性矩；ϕ为横摇角；D（ϕ.）为非线性阻尼力矩，由池田（Ikeda）法求解；Δ为破损舰船的排水量；----GZ（ϕ）为破损舰船对应不同横倾角时的复原力臂，在计算过程中考虑了自由液面的影响，采用局部线性化方法近似；Mwind，tot（t）为风倾力矩；Mwaves（t）为由波浪引起的瞬时作用力矩，采用谱分析法进行求解。

波浪力矩谱SMwaves（ω）按下式计算：

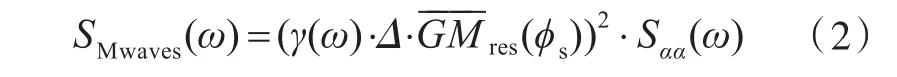
式中：γ（ω）为有效波倾系数；ω为波浪横摇频率；ϕs为破损舰船在定常风作用下的横倾角（平衡角）；------GMres（ϕs）为横倾角ϕs处的初稳性高；Sαα（ω）为波倾角谱。

有效波倾谱可表示为

式中，Szz（ω）为波浪升高谱，国际船模实验水池会议（ITTC）推荐的公式（2014 SDC1会议）［8］为：

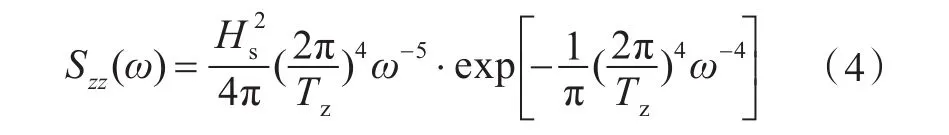
式中：Hs为有义波高；Tz为过零周期。

由风产生的作用力矩可以分为定常风和阵风2部分。其中，由定常风产生的横倾力矩及对应的作用力臂公式如下：

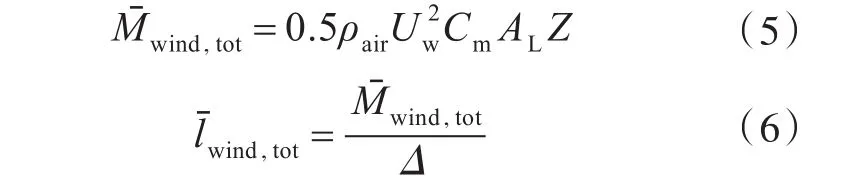
式中：ρair为空气密度，取 ρair=1.222 kg/m3；Uw为平均风速；Cm为横倾力矩系数，一般取Cm=1.22；AL为横向受风面积；Z为横向受风面积AL的形心至水线以下侧面积形心的距离，或近似到平均吃水一半处的距离。

阵风作用采用Davenport风谱表示［12］：

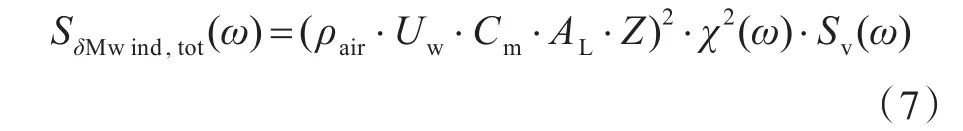
式中，χ（ω）为气动导纳系数。阵风谱Sv（ω）由下式获得：

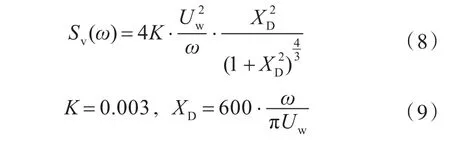
式中：K为非定常风系数；XD为气动导纳系数。

1.2求解横摇运动特性

风、浪联合的力矩谱可由下式表示：

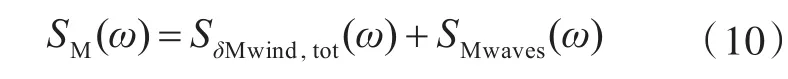
无因次风、浪联合力矩谱可表示为

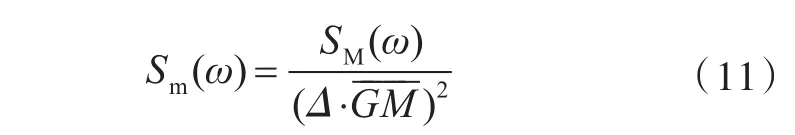
相对 ϕs的横摇角谱Sx（ω），可由下式得到：

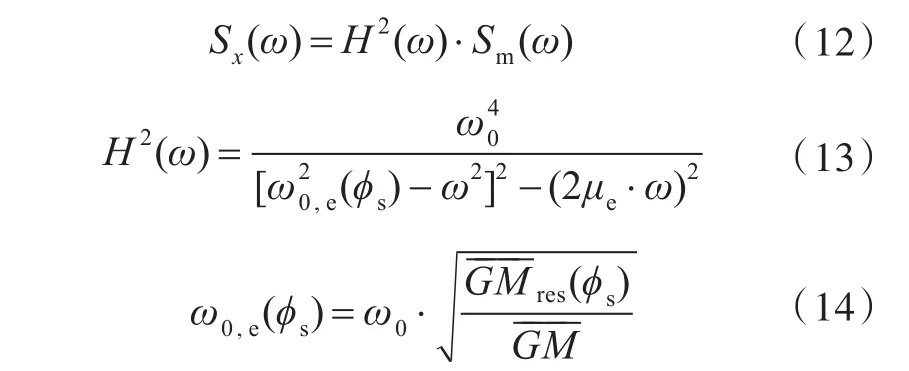
式中：ω0为横摇固有频率；H（ω）为横摇幅值算子；μe为阻尼系数；ω0，e（ϕs）为平衡角ϕs处修正后的横摇固有频率。

横摇角速度标准差σx.可表示如下：

代入式（11）和式（13），即为

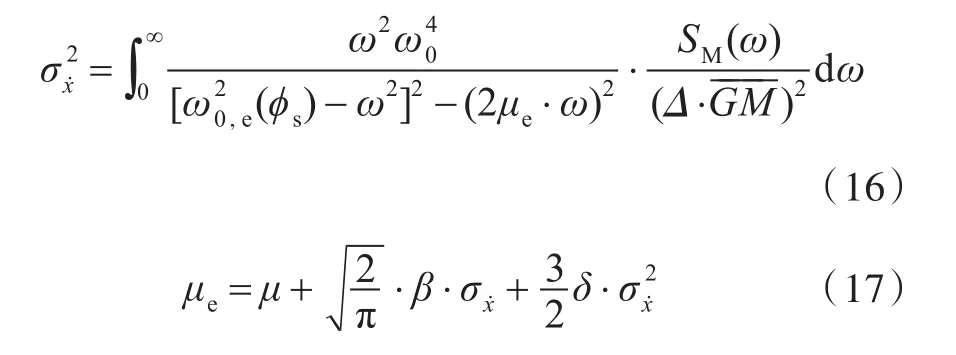
式中：μ为线性横摇阻尼系数；β为二次横摇阻尼系数；δ为三次横摇阻尼系数。横摇角速度标准差σx.根据式（16），通过迭代计算得到。

横摇角标准差σx可按下式计算得到：

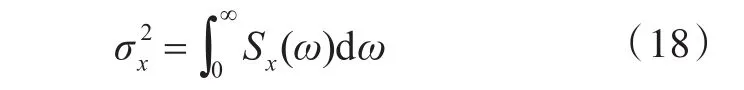
1.3倾覆概率计算

对破损后的GZ曲线，按“等效面积法”处理，以求得等效的倾覆角。复原力臂的线性化处理如图1所示（图中，ϕV，+和ϕV，-分别为左、右舷静水稳性消失角），破损后或因不对称进水而产生的横倾角ϕh，加上因定常风的作用而产生的静平衡角ϕs，可参考完整船恢复力臂曲线的处理方法对复原力臂进行等效化处理。

给定某一环境下的倾覆指数可表示为

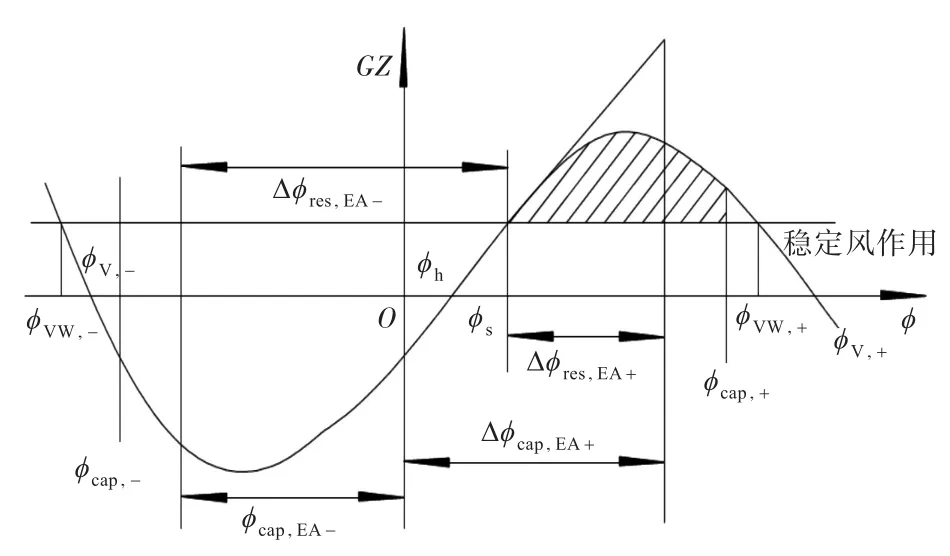
图1　“等效面积法”示意图Fig.1　The calculation method using the“equivalent area”approach

式中：Cs为倾覆指数；Texp为暴露时间，s（本文按1 h=3 600 s计算）；λEA，RIEA+，RIEA-为计算过程中的系数；Tz，Cs为横摇过零周期；σCs为Cs的标准差；Δϕres，EA+，Δϕres，EA-分别为通过“等效面积法”得到的下风侧和上风侧方向正稳性范围；ϕVW，+，ϕVW，-分别为下风侧和上风侧在定常风作用下的稳性消失角；ϕcrit，+，ϕcrit，-分别为下风侧和上风侧的临界角；ϕcap，+，ϕcap，-分别为下风侧和上风侧的最大横摇角；ϕcap，EA+，ϕcap，EA-分别为下风侧和上风侧的等效倾覆角。

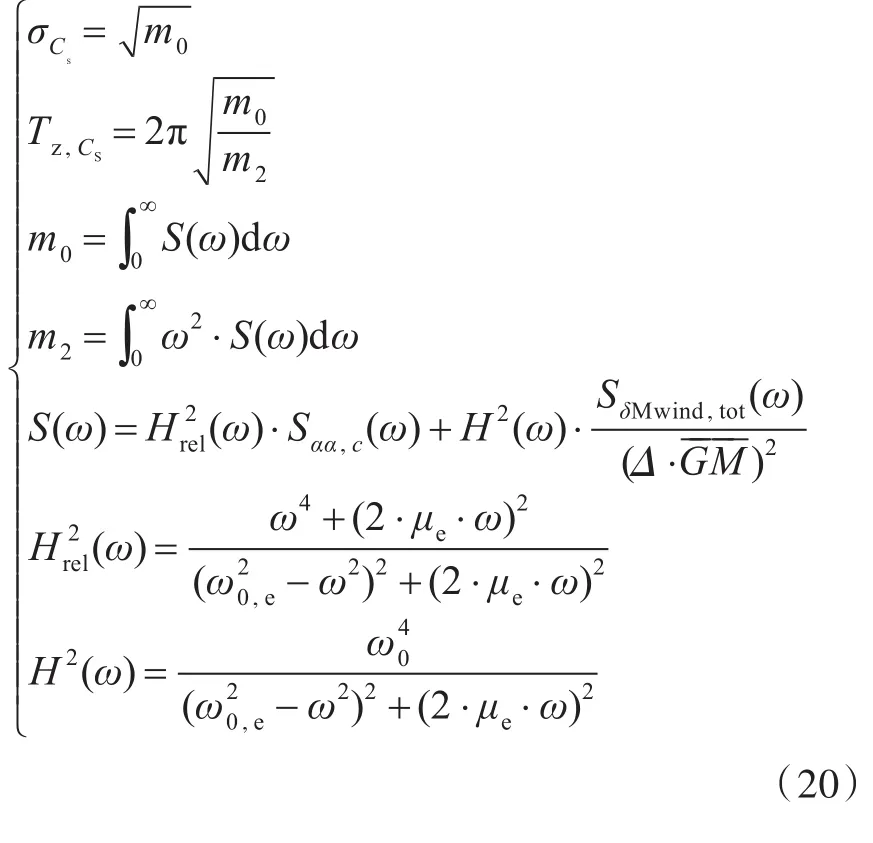
某海区给定暴露时间Texp下的平均舰船倾覆概率CIavg为

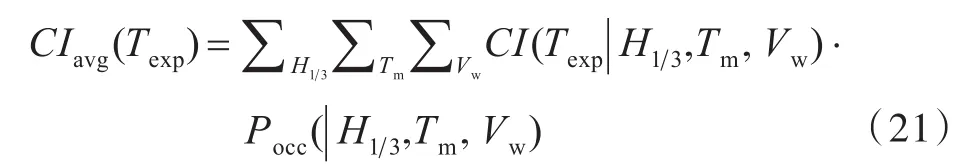
式中：H1 3为有义波高；Tm为模态周期；Vw为风速；Pocc（|H1 3，Tm，Vw）为H1 3，Tm，Vw对应的概率。

2　算例分析

基于论述的方法进行程序开发，本文以某一舰船为例进行破损后的倾覆概率计算。该船标准排水量下的基本参数如表1所示。

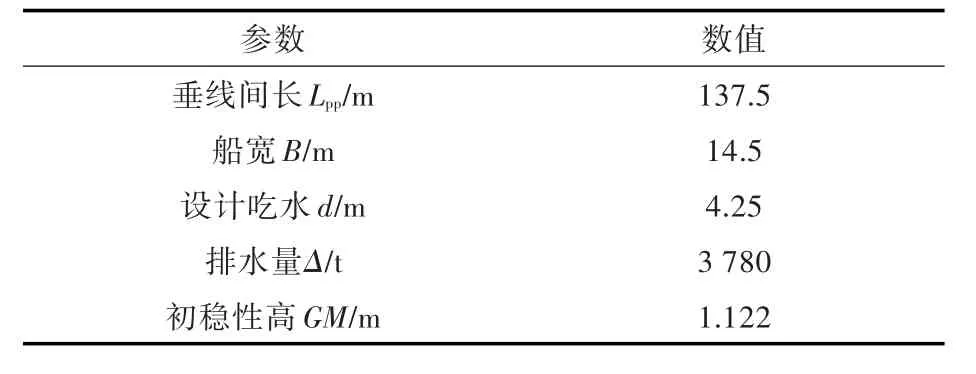
表1　某舰船基本参数Tab.1　Basic parameters

本文假定该船三舱连破，对其进行倾覆概率计算。该船共有14个水密舱壁，分为15个水密隔舱，即共有13个三舱连破舱组（从No.1～No.3到No.13～No.15）。各个三舱连破舱组对称进水后的倾覆概率如图2所示。

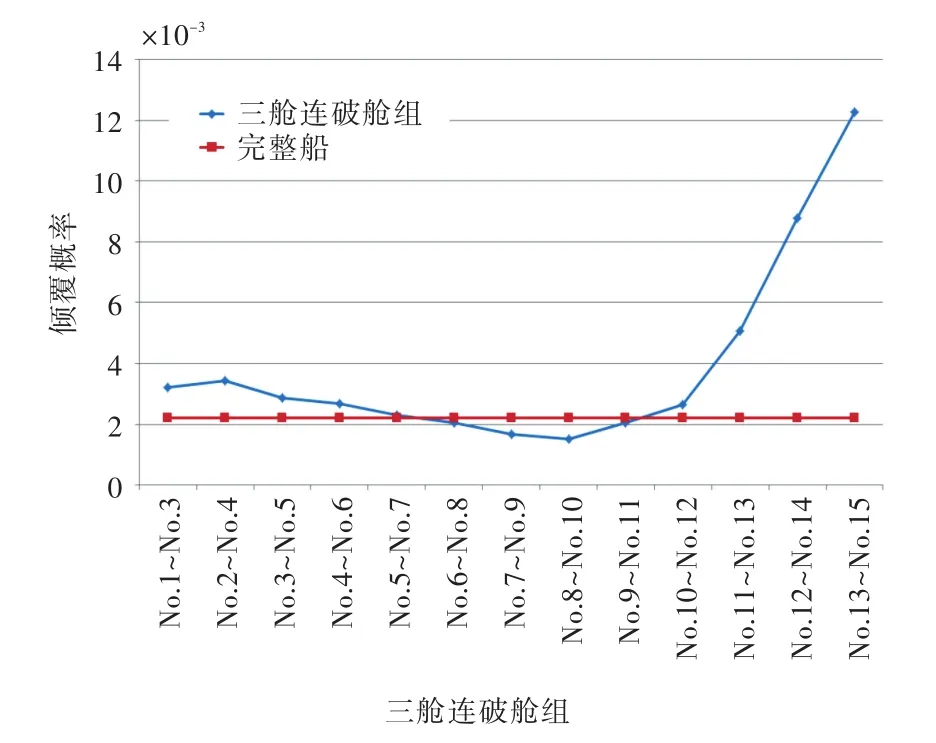
图2　各个三舱连破状态对应的倾覆概率与完整船的倾覆概率比较Fig.2　Comparison of capsizing probability between three-compartment damage and intact ships

由图2可以看出，该船艏艉两端破损后的浮态变化较大，会产生较大的纵倾，破损后的倾覆概率增加明显，尤其是艉部破损情况，增大了一个数量级，这是由复原力臂急剧下降所致（图3）。中间部分破损后，舰船处于“平行”下沉的状态，由计算结果来看，若仅从倾覆指数方面考虑，其与完整船基本相同，这也许是由GZ（考虑舱内水的自由液面）曲线下降、舱内进水自由液面等产生的不利影响与船下沉后受风面积减少，横摇频率减小等有利因素产生的影响基本相当所致（图3、图4）。

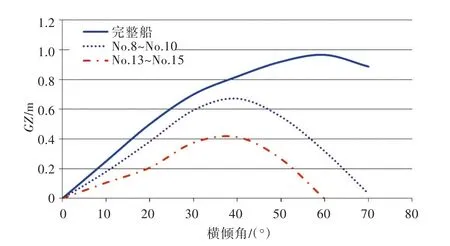
图3　三舱连破后的GZ曲线与完整船的GZ曲线比较Fig.3　Comparison of GZ curves among three-compartment damage and intact ships

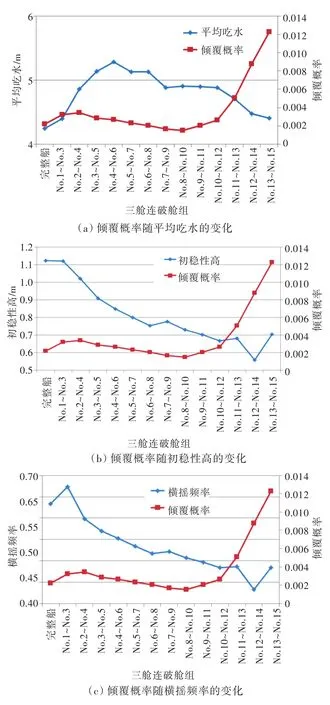
图4　不同破损情况下倾覆概率及主要参数值的比较Fig.4　Comparison of capsizing probability and the main parameters with different damaged conditions

本文选取了几组三舱连破舱组进行不对称进水的倾覆概率研究，计算结果如图5所示。从图中可以看出，与对称进水相比，不对称进水会产生一定的横倾角，导致其倾覆概率急剧增大，这也说明不对称进水是极度危险的，在航行过程中应避免该情况的发生。

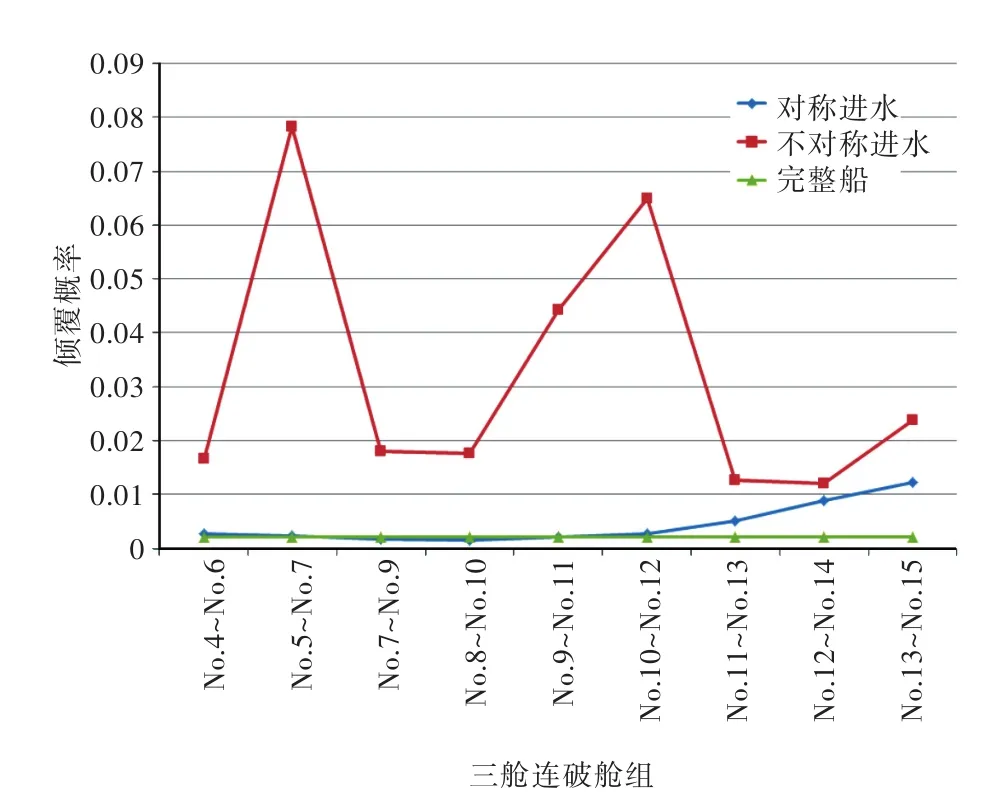
图5　不对称进水和对称进水及完整船的倾覆概率Fig.5　Capsizing probability of intact ship，and the ship with and without symmetrical flooding

3　结　论

用概率论方法对瘫船的稳性进行评价是现代舰船稳性研究的热点之一。本文基于IMO第2代完整稳性最新决议SDC1/INF.6，借鉴完整船瘫船状态下倾覆概率的评估思想，结合舰船破损特点，提出了破损舰船的倾覆概率计算方法。

1）将IMO正在讨论的完整船瘫船稳性第2层薄弱性评估方法拓展到了舰船在某一破损状态下的倾覆概率评估中，建立的倾覆概率计算数学模型适用于对称进水与不对称进水2种情况。

2）通过实例计算，表明对于大部分破损情况来说，对称进水后的倾覆概率会变大，特别是不对称进水情况增加得更为明显，验证了破损舰船瘫船状态更为危险。

3）本文所做的工作可为将来破损舰船瘫船稳性薄弱性衡准研究提供技术支持，为IMO修订新的规范做一些前期的技术储备。

［1］国际海事组织.2008年国际完整稳性规则（2008年IS规则）及其解释性说明［S］.北京：人民交通出版社，2008.

［2］International Maritime Organization.Revision of the in⁃tact stability code，report of the working group（part 1）：IMO SLF 51/WP.2［R］.London：International Mar⁃itime Organization，2008.

［3］顾民，鲁江，王志荣.IMO第二代完整稳性衡准研究的进展综述［C］//2013年船舶水动力学学术会议论文集.北京：中国造船工程学会，2013.

［4］BULIAN G，FRANCESCUTTO A.A simplified modu⁃lar approach for the prediction of the roll motion due to the combined action of wind and waves［J］.Journal of Engineering for the Maritime Environment，2004，218 （3）：189-212.

［5］王田华.内倾船型在波浪中的倾覆特性研究［D］.无锡：中国船舶科学研究中心，2012.

［6］ 王田华，顾民，鲁江，等.内倾船型的瘫船倾覆特性研究［J］.船舶力学，2014，18（4）：363-369. WANG Tianhua，GU Min，LU Jiang，et al.Study on capsizing characteristic of a tumblehome hull under dead ship condition［J］.Journal of Ship Mechanics，2014，18（4）：363-369.

［7］ 曾柯，顾民，鲁江，等.IMO瘫船稳性第二层薄弱性衡准研究［C］//第十三届全国水动力学学术会议暨第二十六届全国水动力学研讨会论文集——F船舶与海洋工程流体力学.上海：上海《水动力学研究与进展》杂志社，2014.

［8］International Maritime Organization.Vulnerability as⁃sessment for dead-ship stability failure mode Submit⁃ted by Italy and Japan：IMO SDC1/INF.6［R］.Lon⁃don：International Maritime Organization，2013.

［9］黄衍顺，汪娟娟，王珊珊.破舱进水对船舶横摇运动的影响［J］.天津大学学报，2012，45（7）：577-584. HUANG Yanshun，WANG Juanjuan，WANG Shan⁃shan.Effects of floodwater on the roll motion response of broken ships［J］.Journal of Tianjin University，2012，45（7）：577-584.

［10］ KORKUT E，ATLAR M，INCECIK A.An experimen⁃tal study of motion behaviour with an intact and dam⁃aged Ro-Ro ship model［J］.Ocean Engineering，2004，31（3/4）：483-512.

［11］PAPANIKOLAOU A，SPANOS D.24th ITTC bench⁃mark study on numerical prediction of damage ship stability in waves preliminary analysis of results［C］// Proceedings of 7th International Workshop on Stabili⁃ty and Operational Safety of Ships.Shanghai：Shang⁃hai Jiao Tong University，2004.

［12］DAVENPORT A G.The spectrum of horizontal gusti⁃ness near the ground in high winds［J］.Quarterly Jour⁃nal of the Royal Meteorological Society，1961，87 （372）：194-211.

Vulnerability assessment for dead-ship stability failure mode of the damaged warship

LV Zhenwang1，2，MA Kun1，2，LI Xinmeng1，2
1 School of Naval Architecture Engineering，Faculty of Vehicle Engineering and Mechanics，Dalian University of Technology，Dalian 116024，China
2 State Key Laboratory of Structural Analysis for Industrial Equipment，Dalian 116024，China

The vulnerability assessment method for dead-ship stability failure mode of intact ships has al⁃ready been proposed by International Maritime Organization（IMO）.However，the relevant method for the damaged ship has not yet been presented due to the complexity of the damaged ship's motion under dead-ship conditions.Based on the theory of the former case，this paper presents a way of assessing the capsizing probability of the damaged warship.The method is then verified with the calculating results of ac⁃tual examples，and the influence of each parameter is discussed.Furthermore，the cases of cross flooding and unsymmetrical flooding are investigated.The method provides certain

for calculating the capsizing probability of the damaged ship.

damaged warship；dead-ship；capsizing probability；damage stability

U661.2+2

A

10.3969/j.issn.1673-3185.2016.02.004

2015-06-23网络出版时间：2016-3-17 10:56

吕振望，男，1984年生，博士研究生。研究方向：船舶破损稳性马坤（通信作者），女，1961年生，博士，教授。研究方向：船舶破损稳性。E-mail：makun@dlut.edu.cn