近场爆炸载荷作用下某大型舰船结构剩余强度分析

田正东，李烨，李朋波，靳易安

1海军装备部，北京100841

2哈尔滨工程大学船舶工程学院，黑龙江哈尔滨150001

近场爆炸载荷作用下某大型舰船结构剩余强度分析

田正东1，李烨2，李朋波2，靳易安2

1海军装备部，北京100841

2哈尔滨工程大学船舶工程学院，黑龙江哈尔滨150001

近场水下爆炸载荷作用下舰船结构的毁伤效应及剩余强度问题一直是业内研究的重点内容之一。首先，对典型舰船设置近场水下爆炸工况，并结合通用FEM软件对近场爆炸载荷下的结构响应进行模拟。然后，根据近场爆炸产生的破口和塑性变形，对典型剖面剖面模数的损失进行分析，发现由近场爆炸引起的毁伤会导致剖面出现8%～10%的剖面模数的损失。最后，对破损舰船浮力重新分布后的波浪弯矩和静水弯矩进行计算，并结合军规对舰船在近场水下爆炸载荷作用后破损情况下的剩余强度进行分析。结果显示，在鱼雷的攻击下，该型舰船依然满足剩余强度要求。

近场水下爆炸；剩余强度；破口；剖面模数

网络出版地址：http://www.cnki.net/kcms/detail/42.1755.TJ.20160317.1056.012.html期刊网址：www.ship-research.com

引用格式：田正东，李烨，李朋波，等.近场爆炸载荷作用下某大型舰船结构剩余强度分析［J］.中国舰船研究，2016，11（2）：33-38.

TIAN Zhengdong，LI Ye，LI Pengbo，et al.Residual strength analysis of vessels under near-field underwater explosion loads［J］.Chinese Journal of Ship Research，2016，11（2）：33-38.

0　引　言

舰船在执行战斗任务的过程中，极易遭受到现代精确制导鱼雷、上浮水雷等大当量水下武器的攻击。从攻击范围来看，这些大都属于近场爆炸，其强大的爆破能力会在距离船体较近位置处造成舰船水下舱室不同程度的破损，使外板出现破口，海水进入舱室从而影响舰船的浮性与稳定性，更严重的，甚至会导致舰船折断沉没。因此，在考虑由近场爆炸载荷引起舰船结构毁伤的前提下，研究舰船所具备的剩余强度对于保证舰船战斗力和抗爆抗冲击能力十分关键［1-2］。李陈峰［3］结合破损舰船的具体特点，分别以Smith法、FEM法以及递增塑性法等为基础，给出了破损舰船剩余承载能力的评估方法。杨平［4］针对几种不同类型的实船，对其破损状态下非对称弯曲渐进崩溃时的剩余强度进行分析，并对影响剩余强度的几种因素进行敏感性分析，取得了客观的效果和指导意义。

在近场爆炸过程中，于舰船外板处产生的塑性变形和破口必然会导致船体剖面模数下降，从而对船体剩余强度造成一定的影响。本文将以某大型舰船（排水量10 000 t左右）为研究对象，结合行业内的校核标准，对船体破损后因破舱进水导致的浮态重新分布，以及因剖面模数的降低对船体各种弯矩造成的影响进行分析，并对剩余强度进行评估，用以为大吨位舰船的近场抗爆抗冲击结构设计提供一定的参考。

1　计算方法和数值模型

由于鱼雷等水下武器对舰船的攻击属近场水下爆炸问题，根据水下近场爆炸的载荷作用特点，可分为冲击波载荷和气泡载荷2种。冲击波载荷会在极短的时间内对舰船局部结构产生较强的局部破坏，而气泡载荷的破坏效应则与爆距有很大的关系［5］。对本文研究的情况而言，气泡载荷主要以气泡射流为主，故通过建立模型的多个时间步的方法来对气泡射流载荷进行加载，且气泡射流以高速运动的圆柱形水流代替，关于射流的宽度、高度以及速度，则可结合相关经验公式或者边界元理论进行确定。因此，将冲击波与射流的双重载荷在不同的时间量级上施加于结构，便可准确分析载荷对舰船结构的冲击动响应。

就水下爆炸冲击波阶段而言，一定爆距下的冲击波压力分布特征可用如下公式［6］确定：

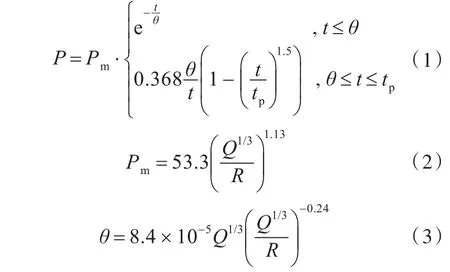
式中：Pm为压力峰值，MPa；t为时间，s；tp为冲击波倒数衰减阶段的终止时刻，s；θ为衰减常数；Q为药包质量，kg；R为爆距，m。

对于射流“水锤”压力大小和速度，引用Plesset等［7］和Blake等［8］提出的公式：

式中：cw和Vi分别为水中声速和射流最大速度，m/s；ρw为水的密度，kg/m3；p∞为爆点位置的静水压，Pa；P为气泡内、外压力差，Pa；pc为饱和蒸汽压，Pa，相比于大气压，其大小通常可以忽略不计。射流的宽度和水动阶段的压力均由上述文献给出，在此不再赘述。

本研究选取的对象为万吨级大型舰船，攻击武器选取为500 kg TNT典型鱼雷战斗部。考虑到舷外流场半径大小对舰船数值模拟精度的影响，设定流场半径为结构半径的6倍［9］。舰船的有限元模型与外部流场之间的耦合情况如图1所示。

图1　舰船有限元模型及与流场耦合示意图Fig.1　Sketch of finite element model of ship and interaction with fluid

对于舰船材料，主要使用船用945钢。考虑到水下近场爆炸属于会产生塑性大变形和破口的高度非线性问题，需要考虑不同条件下的应变率强化问题，因此采用Cowper-Symonds模型作为材料的本构方程：

式中：σy为动应力；σ0为材料静屈服应力；ε.为材料应变率；D，p为与应变率有关的参数［10］，本文分别取为40.4 s-1和5，材料的失效应变取为0.28。

对于爆炸工况，选取L/4，L/2和3L/4（L表示船长）这3个典型剖面处为爆点位置，爆距为0.013L，横剖面处的爆点位置如图2所示。

2　典型武器攻击下毁伤特征

利用有限元软件，将冲击波载荷通过流场与耦合面传递到结构上，以达到模拟水下近场爆炸对大型舰船局部结构的毁伤的目的，爆点位于L/2位置时的破坏情况如图3和图4所示。图3和图4分别给出了中纵位置处半剖的船体内部结构毁伤后的应力云图及船舯位置外板处的应力云图。

图2　爆点位置示意图Fig.2　Sketch of detonation point location

图3　船舯中纵剖面视角破口应力云图Fig.3　Mises stress contours of crevasse of center buttock view

图4　船舯处外板应力云图Fig.4　Mises stress contours of midship plate

由图3和图4可以看出，爆炸载荷导致船体结构出现了大范围的塑性变形，外板向内部严重凹陷并伴随有破口［11-13］。同时，从图3还可以看出，破口出现在大舱室位置处，这样必然会引起破舱进水。并且，由于双层底层间结构的骨架纵横分布不同，导致破口大致呈椭圆形，且其长轴方向与船体纵向一致。将破口尺寸与经验公式［14-15］进行比较并计算相应的误差，发现二者间的误差在工程精度允许范围内，且数值模拟尺寸小于吉田隆［13］计算得到的破口尺寸。破口大小数据如表1所示。

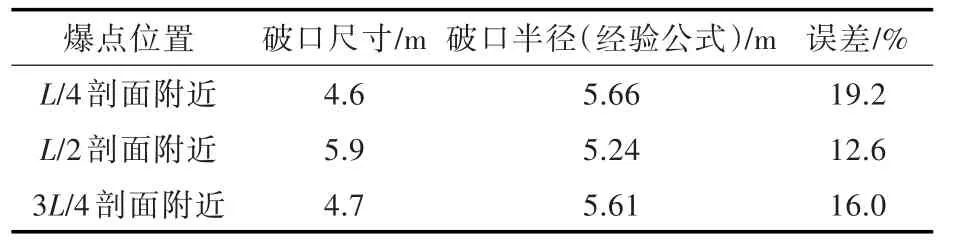
表1　各爆点位置附近破口大小Tab.1　Crevasse size near the blast point

3　局部结构折减横剖面参数计算

船体结构在遭受近场水下爆炸载荷作用时，由于在船体纵向一定区域会出现大面积的塑性变形甚至是破口，典型剖面的承载能力会大大削弱，因此，针对具体剖面需要进行相应的剖面折减，本文中后续计算所使用的数据均取自计算结果。对于破口区域，应当全部纳入失效范围；对于塑性区，根据国军标［15］（GJB 4000-2000）的规定，当船体壳板结构的等效塑性应变达到0.08时，即可认为失去了承载能力。对横剖面的折减方法如图5中曲线所示。

图5　折减系数与材料塑性应变之间的关系Fig.5　Relationship of reduction factor and equivalent plastic strain（PEEQ）

式中：Se为横剖面折减后的面积；S0为横剖面折减前的面积；φ为折减系数；ξP为构件塑性变形；ξmax为破坏塑性应变，即0.08。

将计算所得的各剖面处破损前、后的剖面模数W进行总结，结果如表2所示。由表中数据可以看出，爆炸载荷会导致剖面模数产生10%左右的损失，进一步证明近场爆炸冲击对船体结构产生的损伤较大，也表明了分析剩余强度的重要性。

剖面折减面积计算按下式计算：

表2　各剖面典型参数Tab.2　Typical parameters of three sections

4　舰船破损载荷计算

根据所研究舰船的船型特点，本研究的近场爆炸工况参考了英国劳氏船级社舰船入级规范和规则（简称劳氏规范）的强度标准。主要结合船体剩余强度衡准对船体破损状态进行弯曲应力分析。舰船遭受近场爆炸后，外板等船体板架结构会因承受巨大的冲击载荷而出现破口。因舰船破损属非正常状态，因此与完整船相比，破损舰船以往针对完整舰船的一些强度评估方法明显不再适用。英国劳氏规范提出了目前比较公认的剩余强度校核标准：

式中：σBRS和σDRS分别为船体龙骨处与强力甲板处的弯曲应力，MPa，且

其中：MRRS为剩余强度设计弯矩；ZBRS和ZDRS分别为受损部位甲板剖面模数及龙骨剖面模数；σP为最大垂向允许弯曲应力，MPa，且

其中 fσRS为修正系数，取值0.9。对于船用945钢，σp=405 MPa。

4.1波浪弯矩计算方法

对于遭受近场水下爆炸载荷的舰船，在根据劳氏规范进行弯曲应力计算时，首先需计算剩余强度设计弯矩，公式如下：

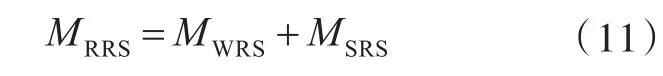
式中：MWRS为破损舰船的波浪弯矩，其中中拱为正，中垂为负；MSRS为破损舰船的静水弯矩。

破损舰船波浪弯矩的计算公式如下：

式中：MW为垂向波浪弯矩最小值；KfRS为剩余强度折减系数，

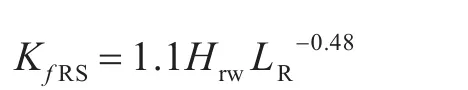
其中：LR为垂线间长；Hrw为能超过的概率为20%的有效波高，Hrw=0.90Hs，其中Hs表示服务海域波高，本文对应的、舰船实际航行情况下选取的服务海域波高为5.5 m。由此，便可计算出折减系数。

垂向波浪弯矩计算公式为

式中：Df为纵向分布系数；Ff为中拱和中垂校正因子；根据劳氏规范的规定可知，波浪弯矩M0由公式 M0=0.1LffsLR2BWL（Cb1+0.7）确定。其中: Lf由 Lf=10.75-（300-LR/100）1.5确定；fs为相对垂向运动的水平修正因子；Cb为方形系数，当Cb＜0.6时，Cb1=Cb，当Cb＞0.6时，Cb1=0.6（Cb1为修正后方形系数）；BWL为水线型宽。

根据劳氏规范，Df在0.4LR～0.65LR之间的取值为1，在0～0.4LR之间和0.65LR时为线性分布，L/4，L/2以及3L/4剖面的Df分别为0.625，1.0 和0.713。Ff的计算与艏飘面积、艉飘面积、船长和船体尾部水线以上的参数相关，具体计算过程可参考劳氏规范校核标准的相关规定进行。给出各剖面处的垂向波浪弯矩及破损波浪弯矩值如表3所示。

表3　典型剖面垂向波浪弯矩Tab.3　Vertical wave bending moment of three typical sections

4.2静水弯矩计算方法

对于船体破损状态下的静水弯矩计算，由于在设定的水下近场爆炸工况下船体舱室会产生相应的破口，水会通过破口在舱室结构与外部水域之间产生对流而导致整个船体的浮力重新分布，故浮态和各剖面的静水弯矩也会相应出现变化。

破舱后，液体进入会导致舱室出现浮力损耗，即Δp=ρgΔv，其中Δp表示船舱破损时船体损失的浮力，ρ表示流入液体的密度。如图6所示，假设水灌到了设计水线（即面积A1及A3的上边线）处，如图所示，取A3与A4面积相等，量取A1与A4所组成矩形的边长，即可计算得到矩形面积，再乘以相应的船舱长L0，即可得到初步损失的舱容体积Δv0。但由于船体进水导致浮力损失时船体需要通过增大吃水才能保证必要的浮力，因此船体吃水也会出现变化，所以，需要经过多次迭代才能进一步提高求解精度。

迭代过程如下：首先，计算出最初的损失舱容Δv0；然后，利用公式Δd0=Δv0/Aw0（其中 Aw0为设计水线面面积）计算出吃水增加的距离Δd0；最后，利用相同的办法计算得到增加的面积 A2。则第1次迭代结果的损失舱容为Δv1=（A1+A2+A4）·L0，之后，再类似地计算出Δd1=Δv1/Aw1。

以采用上述方法计算得到的各个舱室的损失浮力为基础，根据船舶静力学针对破损舰船静水弯矩的计算方法，确定船体破损状态下各剖面的静水弯矩分布如表4所示。表中数值代表药包冲击对应剖面位置产生破口后，所分析的该位置处的破损静水弯矩。

图6　破损舱容计算示意图Fig.6　Sketch of damaged tank capacity calculation

表4　考虑破舱进水后的典型剖面静水弯矩Tab.4　Still water bending moment of three typical sections

5　舰船剩余强度计算

根据前文所述校核方法，将计算所得的破损波浪弯矩以及破损静水弯矩进行整理，然后通过计算得到相应中拱、中垂状态下的剩余强度设计弯矩，并将其代入RSA1校核公式进行计算，相应的计算结果整理如表5所示。

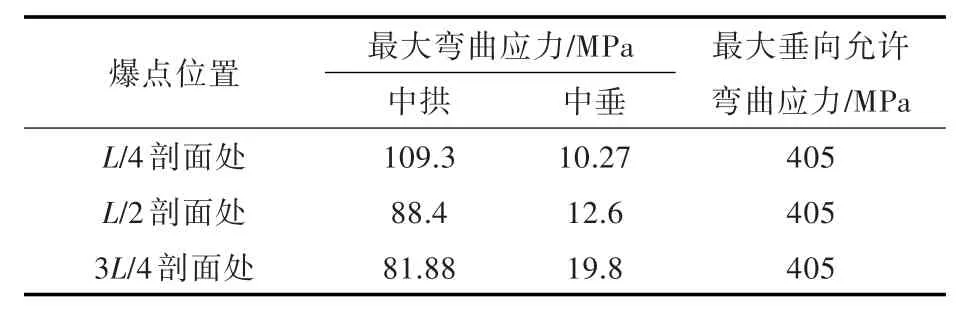
表5　各典型剖面弯曲应力强度校核Tab.5　Bending moment checking of three typical sections

由表5可以看出，无论爆点在L/4剖面、L/2剖面还是3L/4剖面处，在破损状态下，中拱或者中垂最大弯曲应力均未达到最大允许值，即在破损状态下仍能满足船体对剩余强度的要求，能保证一定的舰船生命力。同时还可以看出，中拱状态下产生的弯矩或者弯曲应力明显大于中垂状态下的。因此，相对而言，中拱状态属于考核舰船剩余强度时相对危险的状态，此状态下的强度应引起足够的重视。另外，本舰船使用的材料为船用945钢，其最大允许弯曲应力较大，但中拱时出现的最大弯曲应力（尤其是L/4剖面处）依然能达到最大允许值的20%～30%，而这种比例如果计及水下爆炸冲击动弯矩的话，会对破损状态下的舰船生命力造成严重的威胁。由此可见，部分剖面位置处的剩余强度问题同样也应引起足够的重视。

6　结　论

通过结合有限元软件设置典型工况，对某大型舰船遭受近场水下爆炸载荷的结构损伤进行了模拟，通过结合规范对剩余强度进行分析，得到了以下结论：

1）舰船在遭受500 kg TNT当量的鱼雷近场舷侧攻击时，会产生大范围的塑性变形和破口，破口会引起舱室破坏而导致进水，进而影响浮性和抗沉性。破口大致呈椭圆形，其长轴与纵向平行。

2）对于本文所分析的某大型舰船而言，在水下近场爆炸载荷下，典型剖面因为破口的出现会损失10%左右的剖面模数，船体强度会出现一定程度的削弱。通过结合劳氏规范进行校核，发现在各工况破损状态下舰船仍满足剩余强度的要求。

3）通过对各剖面弯矩进行分析，发现中拱状态下的弯矩及弯曲应力远大于中垂状态下的，因此，对于中拱状态下艏部剖面处的剩余结构强度，要引起足够的重视。

［1］ 冯麟涵，姚熊亮，汪玉，等.基于本征函数的舰船冲击环境工程化预报方法［J］.中国造船，2010，51（3）：65-76. FENG Linhan，YAO Xiongliang，WANG Yu，et al.En⁃gineering prediction method of ship impulsive environ⁃ment based on empirical eigenfunction［J］.Shipbuild⁃ing of China，2010，51（3）：65-76.

［2］ 唐廷，朱锡，侯海量，等.大型水面舰艇防雷舱结构防护机理数值仿真［J］.哈尔滨工程大学学报，2012，33 （2）：142-149. TANG Ting，ZHU Xi，HOU Hailiang，et al.Numerical simulation study on the defense mechanism of a cabin near the shipboard for large surface vessels［J］.Journalof Harbin Engineering University，2012，33（2）：142-149.

［3］ 李陈峰.破损舰船剩余强度评估方法研究［D］.哈尔滨：哈尔滨工程大学，2009.

［4］杨平.船体结构极限强度及破损剩余强度的研究［D］.武汉：武汉理工大学，2005.

［5］ ZHANG A M，WANG S P，HUANG C，et al.Influences of initial and boundary conditions on underwater explo⁃sion bubble dynamics［J］.European Journal of Mechan⁃ics-B/Fluids，2013，42：69-91.

［6］冯麟涵，汪玉，杜俭业.水面舰艇非典型安装设备冲击环境特征［J］.哈尔滨工程大学学报，2012，33（8）：972-977. FENG Linhan，WANG Yu，DU Jianye.Impulsive envi⁃ronment characteristics of a typical installed equip⁃ment on board［J］.Journal of Harbin Engineering Uni⁃versity，2012，33（8）：972-977.

［7］PLESSET M S，CHAMPMAN R B.Collapse of an ini⁃tially spherical vapor cavity in the neighborhood of a solid boundary［J］.Journal of Fluid Mechanics，1971，47：283-290.

［8］BLAKE J R，GIBSON D C.Cavitation bubbles near boundaries［J］.Annual Review of Fluid Mechanics，1987，19（2）：99-123.

［9］姚熊亮，徐小刚，张凤香.流场网格划分对水下爆炸结构响应的影响［J］.哈尔滨工程大学学报，2003，24 （3）：237-240，244. YAO Xiongliang，XU Xiaogang，ZHANG Fengxiang.In⁃fluence of fluid gridding on structural response of un⁃derwater explosion［J］.Journal of Harbin Engineering University，2003，24（3）：237-240，244.

［10］JONES N.Structural impact［M］.New York：Cam⁃ bridge University Press，1989.

［11］ RAJENDRAN R，NARASIMHAN K.Damage predic⁃tion of clamped circular plates subjected to contact underwater explosion［J］.International Journal of Im⁃pact Engineering，2001，25（4）：373-386.

［12］张伦平，张晓阳，潘建强，等.多舱防护结构水下接触爆炸吸能研究［J］.船舶力学，2011，15（8）：921-929. ZHANG Lunping，ZHANG Xiaoyang，PAN Jianqiang，et al.Energy research about multicamerate defence structure subjected to underwater contact explosion ［J］.Journal of Ship Mechanics，2011，15（8）：921-929.

［13］ 吉田隆.二次世界大战初期日本海军舰船在炸弹攻击下的损伤实例分析［J］.船の科学，1990（5）：70-81.

［14］朱锡，白雪飞，黄若波，等.船体板架在水下接触爆炸作用下的破口试验［J］.中国造船，2003，44（1）：46-52. ZHU Xi，BAI Xuefei，HUANG Ruobo，et al.Crevasse experiment research of plate membrance in vessels subjected to underwater contact explosion［J］.Ship⁃building of China，2003，44（1）：46-52.

［15］ 总装备部军兵种部海军局.舰船通用规范1组船体结构：GJB 4000-2000［S］.北京：总装备部军标出版发行部，2000.

［16］CUI H W，YANG P.Residual ultimate strength of ship plates under cyclic in-plane compressive loading ［J］.Journal of Huazhong University of Science and Technology（Natural Science Edition），2015，43（4）：108-112.

Residual strength analysis of vessels under near-field underwater explosion loads

TIAN Zhengdong1，LI Ye2，LI Pengbo2，JIN Yian2
1 Naval Armament Department of PLAN，Beijing 100841，China
2 College of Shipbuilding Engineering，Harbin Engineering University，Harbin 150001，China

The damaging effect and residual strength of ships under the near-field underwater explosion loads has remained as one of the most crucial subject in the field of vessel research.In this paper，the struc⁃tural response under explosive loads is simulated based on the common FEM software by assuming a typi⁃cal near-field condition of underwater explosion.Loss of the modulus for typical sections is then analyzed according to the crevasse and plastic deformation results of near-field blast，and the loss is within 8%～10%.The wave bending moment and still water bending moment are also calculated after the buoyancy re⁃distribution.Finally，the residual strength in the damaged cases is analyzed simultaneously for the near-field underwater explosion combined with military regulations.The results show that the vessel still meet the requirements of residual strength under torpedo attack.

near-field underwater explosion；residual strength；crevasse；section modulus

U661.43

A

10.3969/j.issn.1673-3185.2016.02.006

2015-08-12网络出版时间：2016-3-17 10:56

田正东，男，1972年生，博士，工程师。研究方向：舰船总体研究与设计

李烨（通信作者），男，1990年生，硕士生。研究方向：船舶与海洋结构物力学性能。

E-mail：liyehit2010@sina.com