加权Markov链在农产品生产价格指数中预测研究

兰冲锋，张　冕

（1.北京邮电大学 经济与管理学院，北京100876；2.阜阳师范学院 经济学院，安徽 阜阳236037；3.区域物流规划与现代物流工程安徽省重点实验室，安徽 阜阳 236037；4阜阳师范学院 数学与统计学院，安徽 阜阳 236037）

加权Markov链在农产品生产价格指数中预测研究

兰冲锋1，2，3，张冕4

（1.北京邮电大学 经济与管理学院，北京100876；2.阜阳师范学院 经济学院，安徽 阜阳236037；3.区域物流规划与现代物流工程安徽省重点实验室，安徽 阜阳 236037；4阜阳师范学院 数学与统计学院，安徽 阜阳 236037）

首先根据农产品生产价格指数具有随机性的特点，利用均等概率的方法建立其状态等级；接着针对农产品生产价格指数为相依随机变量的特点，计算其规范化的多阶自相关系数；最后用加权的Markov链模型来预测未来农产品生产价格指数变化趋势，并得出了农产品生产价格指数落在区间［99.91，104.56）内最为稳定的结论。

Markov链；加权；农产品生产价格指数；预测

随着国家经济的快速持续发展，我国对农产品消耗逐渐增大，农产品价格稳定对促进中国经济的发展具有十分重要的意义。为了及时监测农产品市场的价格走势，客观准确地反映农产品的市场价格变化情况和农业生产者实际劳动所得，更好地为国家各级党政部门的宏观决策提供服务，国家统计部门经过三年的实践和调整，决定从2003年第二季度开始，面向全社会按季发布全国农产品生产价格指数。通过该指数的发布，不仅可以客观反映出我国农业生产者出售农产品价格水平的变动趋势及幅度，而且能够体现出农产品生产价格水平和结构变动情况，满足农业与国民经济核算的需要。因此，通过对农产品生产价格指数的研究，可以分析预测农产品价格波动情况，及时合理地调整农产品价格，充分调动农民生产的积极性，促进我国宏观经济的稳定发展。

对农产品生产价格的研究，目前主要是从农产品价格波动和影响因素等方面来进行分析的。如王孝松和谢申祥［1］证实了国际农产品价格对国内农产品价格产生了的显著影响，并提出了一些有效措施来平抑国际市场价格波动而带来的国内农产品价格上涨；顾国达和方晨靓［2］利用Markov局面转移向量误差修正模型实证分析了国际市场因素影响下中国农产品价格波动的特征；而温涛和王小华［3］则认为货币政策对中国农产品价格产生了比较强烈的冲击效应。而关于各类价格指数的预测，现有的文献主要采用灰色预测法和时间序列模型（ARIMA）等方法进行分析预测［4-5］。虽然这些方法也能够对农产品生产价格指数进行预测，但是都难以反映价格指数客观变化的随机性，然而分析预测的实质恰恰就是要求对经济运行过程中所出现的随机过程进行处理，并据此推断其将来的趋势变化。Markov链就是对动态变化的随机现象进行预测一种方法，但是该预测方法主要集中在降水预测以及自然灾害变化中［6～8］，用于农产品生产价格指数方面的预测研究则较为鲜见，仅有谌贻庆和徐鑫［9］用Markov链模型对农产品生产价格指数中做出了预测。本文则对此做出两点改进：一是对样本数据Markov链状态区间划分摒弃了主观因素，使得划分结果更为公正；二是采用了加权的Markov链预测，结果更为准确。

基于上述考虑，本文针对农产品生产价格指数变化的特点，通过均等概率的方法建立其状态等级，采取规范化的各阶自相关系数为权数，用加权Markov链的研究方法来预测农产品生产价格指数的未来变化状况。

1　加权Markov链预测的基本原理

1.1Markov链

Markov链是数学中具有马尔科夫性的一类重要随机过程，在该过程中，给定当前知识或信息，过去的信息（即当前以前的历史状态）对于预测将来的走势（即当前以后的未来状态）是无关的，即“将来”与“过去”是相互独立的。Markov链的定义如下［10］：

设｛Xn，n∈T｝是一族定义在概率空间（K，F，P）上取值于E的随机变量，E为可数集，T=｛0，1，2，…｝为时间参数集，如果对任意的n≥2，0≤t1＜t2＜…＜tn及任意 i1，i2，…in∈E都有：则称｛Xn，n∈T｝是一个Markov链，E为其状态空间。

如果Markov链的一步转移概率Pij（n）与n无关，即P（Xn+1=j|Xn=i）=Pij，i，j∈E，则称此Markov链为齐次Markov链。在实际应用中，一般只考虑齐次的Markov链，齐次Markov链｛Xn，n∈T｝的有限维分布只与其一步状态转移概率矩阵Pij（i，j=0，1，…）以及初始分布｛P（i），i=0，1，…｝有关，即只要知道其状态转移概率矩阵以及初始分布，我们就可以计算出系统处于每个状态的概率，从而为相关决策提供理论依据。

1.2加权Markov链预测原理

由于农产品生产价格指数所处状态转移过程是随机的，故可将其看成一列相依随机变量，则农产品生产价格指数的各阶自相关系数的大小就刻画了各时段价格指数之间相关关系的强弱。因此，根据前面若干时段农产品生产价格指数（对应的状态），我们可以对该时段农产品生产价格指数状况进行分析预测，并根据前面各个时段与该时段相关关系的强弱来确定权数，再进行加权求和，即可达到对农产品生产价格指数进行预测之目的。

2　加权Markov链预测的基本步骤

利用上述思路，可把加权Markov链预测的基本步骤概括为：

步骤1划分样本数据状态等级。文献［9］采用的均等区间划分的方法来对样本数据进行状态等级划分，主观性较强，缺乏一些理论依据，而文献［7］是根据具体问题的特征进行划分的，但该方法只能应用于有明显特征的数据序列，因此它的应用范围比较狭窄。假如按照农产品生产价格指数的大小进行升序排列，我们可以看出样本数据的分布近似为正态分布。因此本文假定农产品生产价格指数服从正态分布，使用均等概率划分的方法，使随机变量的值落在任意一个状态区间的概率相同。我们并不是按照均分法［9］采用的各区间跨度的相同长度来划分等级，而是按照各个状态区间跨度的相同概率来划分等级，该方法可保证状态区间划分的客观性，很好地规避了均分法因划分区间偏好对预测结果产生的主观影响。

步骤2按步骤1中所划分的状态标准，确定各个季度农产品生产价格指数的所处的状态等级。

步骤 3“马氏性”检验：对于随机序列｛Xn，n≥0｝，用 fij表示在（X1，X2，…，Xn）中从状态i经过一步转移到状态j的频数，记，则当n较大时，统计量 χ服从自由度为（n-1）2的 χ2分布，选定了置信度 α，查表得符合马氏性，否则认为该过程不是Markov链［11］。

步骤4若通过了第3步的检验，则按步骤2所得到的状态序列，生成不同步长的Markov链的转移概率矩阵。

步骤6依据前面若干季度的农产品生产价格指数值作为初始状态，结合其各自步长的转移概率矩阵，即可预测出该季度农产品生产价格指数值的状态概率，k为滞时（步长），k=1，2，…，m。然后将同一状态的各预测概率加权求和，并以此作为农产品生产价格指数处于该状态的预测概率，即， max｛Pi，i∈E｝所对应的即为该季度农产品生产价格指数的预测状态。待该季度取得农产品生产价格指数之后，将其加入原序列，再重复前面的步骤1-6，即可进行下一季度价格指数的预测。

步骤7应用Markov链遍历性定理，求出农产品生产价格指数的极限分布，进而分析其分布特征。

3　实例分析

从中国统计年鉴上得知，农产品生产价格指数自2003年创立至2015年第二季度，共计取得50个季度的数据，我们选取前49个季度的数据进行分析预测。具体数据资料如表1所示。

表1　全国农产品生产价格指数

（1）划分样本数据的状态等级。采取均等概率划分的方法，考虑到样本数据的个数我们可以将其划分为五种状态。为此我们先计算出样本数据的均值x-=106.57和标准差s=7.916 3，接着查出标准正态分布表的分位点 u0.8=0.841 6，u0.6=0.255 3，最后计算出五种状态等级划分结果如表2所示。

表2　全国居民消费价格指数状态分级表

（2）根据表2划分的状态标准，我们可以确定各个季度农产品生产价格指数所处状态，结果如表1中“状态”栏所列。

（3）对农产品生产价格指数资料序列做Markov性检验。根据表1的资料可得到农产品生产价格指数的一步转移频数矩阵（fij）和一步转移概率矩阵P（1）如下：

5（16），统计结果显著，故满足马氏性，可以利用Markov链来处理农产品生产价格指数。

（4）由步骤3得到的一步转移概率矩阵，可以生成不同步长的Markov链的转移概率矩阵如下：

（5）由表1可计算出农产品生产价格指数五阶自相关系数和五种步长的Markov链权重，结果见表3。

表3　各阶自相关系数和各种步长的Markov链权重表

（6）根据2014年四个季度和2015年第一季度的全国农产品生产价格指数及相应状态转移概率矩阵对2015年第二季度全国农产品生产价格指数及所处状态进行预测，结果如表4所示。

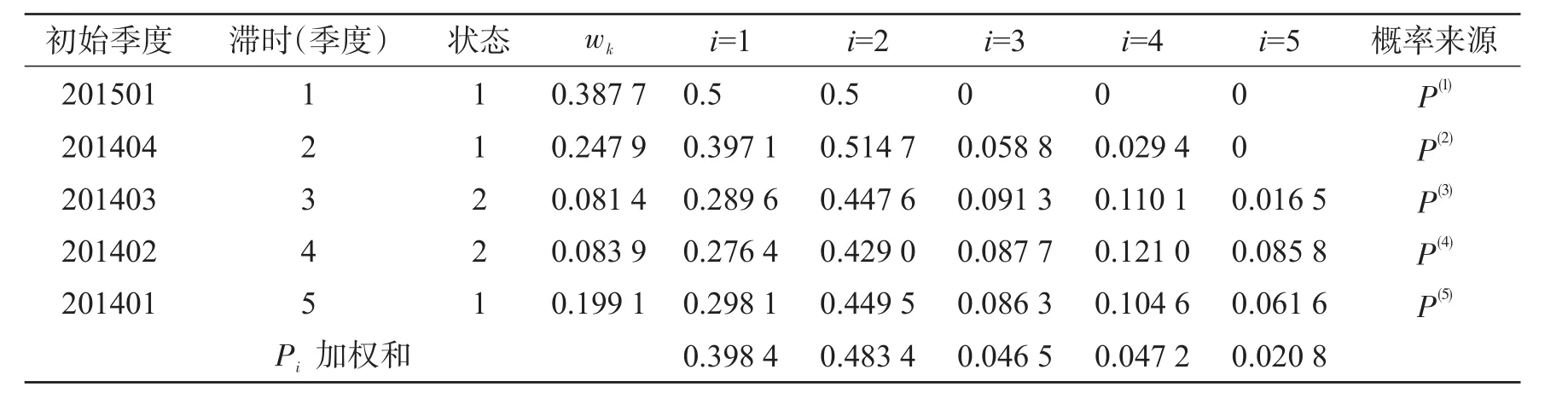
表4　2015年第二季度全国农产品生产价格指数预测表

由表 4可知，max｛Pi，i∈E｝=0.483 4，此时i=2，可见2015年第二季度全国农产品生产价格指数预测状态为2，即该季度农产品生产指数在99.91-104.56之间，而2015年第二季度农产品生产价格指数是101.5，预测结果与实际情况吻合，这说明应用本文的方法进行农产品生产价格指数状态的预测是切实可行的。同理，我们把2015年第二季度农产品生产价格指数101.5加入原序列中，再重复前面的预测步骤1-6，即可进行2015年第三季度价格指数的预测。限于篇幅，我们仅给出预测结果仍为状态2。

4　结束语

农产品生产价格指数的变动是多种因素的相互作用的结果，因而具有动态性和随机性等多重不确定性，所以对农产品生产价格指数进行分析预测具有一定的难度。与普通的Markov链预测方法对比，本文所使用的预测方法以各阶自相关系数为权重，用不同步长的加权Markov链预测系统的状态，能更有效地利用原始数据信息，大大提高了Markov链预测的合理性以及准确性。另外，本文所使用的均等概率划分状态区间的方法，对于没有明显特征的时间序列数据的处理，也提供了一种客观公正的分类方法。然而，加权Markov链的预测结果为农产品生产价格指数的某一个状态（是一个区间值），这虽然扩大了预测的范围，提高了预测的可靠性，但是如何根据最后计算出的状态概率分布求出农产品生产价格指数的点估计值仍是一个需要解决的问题。

［1］ 王孝松，谢申祥.国际农产品价格如何影响了中国农产品价格？［J］.经济研究，2012，47（3）：141-153.

［2］ 顾国达，方晨靓.中国农产品价格波动特征分析--基于国际市场因素影响下的局面转移模型［J］.中国农村经济，2010（6）：67-76.

［3］ 温涛，王小华.货币政策对中国农产品价格波动的冲击效应研究［J］.当代经济科学，2014，36（6）：20-29.

［4］ 杨颖梅.基于ARIMA模型的北京居民消费价格指数预测［J］.统计与决策，2015（4）：76-78.

［5］ 丛春霞，李秀芳.灰色预测在股票价格指数预测中的应用［J］.中国统计，2000（5）：15-17.

［6］ Liu H，Chen X S.Application of stochastic process in disastrous forecasting［J］.Systems Engineering-Theory and Practice，1996，9（9）：19-23.

［7］ 孙才志，张戈，林学钰.加权马尔可夫模型在降水丰枯状况预测中的应用［J］.系统工程理论与实践，2003，23（4）：100-105.

［8］ 茹正亮，杨芝艳，朱文刚，等.加权马尔科夫ARGARCH-GED模型在降水量中的预测［J］.系统工程，2013，31（12）：98-102.

［9］ 谌贻庆，徐鑫.马尔可夫链在农产品生产价格指数中的应用［J］.统计与决策，2012（8）：90-92.

［10］胡迪鹤.随机过程理论基础应用［M］.武汉：武汉大学出版社，2000：78-149.

［11］艾山江·沙依提，韩东，朱维宝.股票价格变动的马氏链分析［J］.经济数学，1996，13（1）：112-116.

Prediction of index of producers'prices of agricultural products with weighted Markov chain

LAN Chong-feng1，2，3，ZHANG Mian4

（1.School of Economics and Management，Beijing University of Posts and Telecommunications，Beijing 100876，China；2.School of Economics，Fuyang Normal University，Fuyang Anhui 236037，China；3.Anhui Provincial Key Laboratory Regional Logistics Planning and Modern Logistics Engineering，Fuyang Anhui，236037 China；4.School of Mathematics and Statistics，Fuyang Normal University，Fuyang Anhui 236037，China）

Firstly，according to the random feature of index of producers'prices of agricultural products，this paper establishes the state level by the method of average probability.Then the paper calculates several stage normalized autocorrelation coefficient of index of producers'prices of agricultural products based on its characteristics of dependent random variables.Finally，the weighted Markov chain model is used to predict the future trend of index of producers'prices of agricultural products and the conclusion is gotten that the index of producers'prices of agricultural products is the most stable in the interval［99.91，104.56）.

Markov chain；weighted；index of producers'prices of agricultural products；prediction

F304.2；O211.62

A

1004-4329（2016）02-097-05

10.14096/j.cnki.cn34-1069/n/1004-4329（2016）02-097-05

2015-09-14

安徽省高校自然科学研究重点项目（KJ2015A182，KJ2016A876，KJ2015A191）；安徽省质量工程项目（2013zy 167）；阜阳师范学院质量工程项目（2014JYXM45）；阜阳师范学院科研项目（2014WLGH02）资助。

兰冲锋（1981－），男，硕士，讲师，研究方向：概率统计、供应链管理。