压裂管柱轴向变形的理论计算及应用

李琪李旭阳王再兴张永忠

1.西安石油大学石油工程学院；2.长庆油田公司第一采油厂

压裂管柱轴向变形的理论计算及应用

李琪1李旭阳1王再兴1张永忠2

1.西安石油大学石油工程学院；2.长庆油田公司第一采油厂

引用格式：李琪，李旭阳，王再兴，张永忠. 压裂管柱轴向变形的理论计算及应用［J］.石油钻采工艺，2016，38（4）：467-472，486.

综合分析压裂作业过程中影响管柱轴向变形的因素，从实际作业工况出发，考虑各因素的动态变化，结合弹塑性力学，利用划分微元后叠加的方法，建立了压裂管柱轴向变形的理论计算模型，并以陈平15-2井水力喷射分段压裂为例进行了实例计算，根据计算结果可准确地进行井下作业定位、校核作业工具强度以及确定伸缩补偿距，对现场生产作业具有重要的指导意义。

管柱受力；轴向变形；压裂；作业定位

井下压裂作业过程中，受管柱自重、浮力、摩阻力、温度效应、活塞效应、膨胀效应和屈曲效应的影响，作业管柱会发生轴向变形，导致坐封位置与设计位置不符，从而影响压裂效果。井下管柱深度通常是通过人工地面测量，同时配合电磁测井曲线来校正管柱下入深度及封隔器卡封的准确位置［1］。测磁定位曲线影响因素多、曲线解释困难、作业工作量大、占用生产时间长、成本较高，特别是测试解释数据和人工测量数据相差较大时难以给出解释，准确度不高［2］。而且，磁定位未能考虑电缆的伸长及坐封、压裂过程管柱的轴向变形。因此，准确计算作业过程中不同因素影响下管柱的轴向变形量，对进一步优化压裂方案、提高压裂施工成功率具有重要意义。目前对计算直井中作业管柱轴向变形的研究比较多，但对水平井的研究较少，水平井的模型建立较为复杂［3］；很多研究只考虑单一因素的影响、考虑因素不全［4］；相关的研究也都不严格地按照作业流程计算，未实时计算作业过程中温度、压力等的动态变化［5］。必然导致轴向应力和轴向变形的计算产生一定误差。在以往研究基础上，以水平井水力喷射压裂作业为例，以弹塑性力学理论为基础，利用划分微元计算后叠加的方法，改进了压裂管柱轴向变形的理论计算模型，并进行了实例计算，根据计算结果可准确确定坐封位置，校核管柱强度，保证压裂作业准确、安全进行。

1　模型的建立Model construction

1.1作业流程及影响因素分析

Work procedures and analysis on influencing factors

（1）管柱下入过程。此过程通过油管将作业管柱下入井下，作业管柱下端处于自由状态且开口，管柱内外压力平衡，影响管柱轴向变形的因素有管柱自身的重力效应、浮力效应及温度效应。

（2）坐封过程。此过程通过油管内加压坐封，管柱内压大于外压，在内外压差作用下产生膨胀效应和活塞效应。另外，由于单流阀的存在，作业管柱下端封闭，重力效应和浮力效应的计算也将发生变化。

（3）压裂过程。此过程压裂液通过管内注入进行压裂，液体注入时在管柱内壁产生摩阻，随着注入液流量和性质的变化，温度和压力也随之产生动态变化，当有效轴向力大于屈曲载荷时管柱发生正弦屈曲或螺旋屈曲，这些都会导致作业管柱的轴向变形。但由于坐封后作业管柱的位置不再发生变化，之前产生的预应力和变形永久存在，此过程中，本应产生的轴向变形将转化成力的形式作用于封隔器，因此需对封隔器进行强度校核。

（4）反洗井过程。从油套环空注入洗井液，不断冲洗井壁与井底，将压裂残余物带出地面，保证井筒和井底的清洁。此过程中受重力效应、浮力效应、温度效应、摩阻效应的影响。

1.2假设及处理

Assumptions and processing

（1）压裂作业管柱及其附件均是弹性变形体。

（2）管柱轨迹变化与井眼轨迹一致。

（3）将作业管柱作微元段划分。对于整个管柱，不同部位所受各因素影响不同，多种基本效应的组合也不能简单的叠加；对于一个微单元，却可以根据该单元的位置直接确定该单元上受到的各种基本效应，从而计算出微元段管柱的轴向变形，最后叠加得到总的变形。

（4）将作业流程作多步划分。在实际作业过程中，作业管柱的变形不仅与位置有关，而且与时间也相关。井下的温度压力等都处于动态变化过程，管柱的轴向变形量将随着作业流程的变化而改变。因此，为了得到实际准确的计算结果，将作业流程进行多步划分，计算不同过程中的实时变化，最后得实际的准确值。

1.3下入过程管柱轴向变形计算

Calculations of pipestring axial deformation during tripping in

此过程中作业管柱的轴向伸长受重力效应、浮力效应、温度效应及活塞效应的影响。重力效应中的重力为管柱自重；由于管柱下端开口浮力效应的浮力按环形柱体排开液体计算；温度效应中的温度为地层温度。另外，对于大位移井、长水平段水平井，作业管柱下入过程中还需考虑管外壁与套管壁的摩阻效应，当有效轴向力大于屈曲载荷时还需考虑屈曲效应。

（1）重力效应

任意i个微元段等效垂深之和

井下任意深度h处等效重力

轴向应力

重力效应引起的轴向变形

式中，i为任意微元段个数；Hv为完钻垂直井深，m；D为管柱外径，m；d为管柱内径，m；qs为管柱线重，N/m；θi为微元段井斜，°；hi为微元段长度，m。

（2）浮力效应

井下任意深度h处等效浮力

轴向应力

浮力效应引起的轴向变形

式中，ρ0为管外液体密度，kg/m3。

（3）温度效应

微元段管柱温度分布［6］

温度效应引起的轴向变形

式中，Tui为微元段管柱顶部初始温度，℃；Tdi为微元段管柱底部初始温度，℃；Tuf为微元段管柱顶部最终温度，℃；Tdf为微元段管柱底部最终温度，℃；Ti为微元段管柱初始温度，℃；Tf为微元段管柱最终温度，℃；α为材料热膨胀系数，无因次。

1.4坐封过程管柱轴向变形计算

Calculations of pipestring axial deformation during seating

此过程中作业管柱的轴向变形继续受重力效应、浮力效应的影响，但由于管柱末端封闭，此时的重力为管柱自重和管内液体重力的合力，浮力按整个管柱排开液体体积计算。另外，随着内压的增大，管柱的轴向变形将受到活塞效应和膨胀效应的影响。具体计算模型如下：

（1）重力效应

井下任意深度h处等效重力

重力产生的轴向应力为

重力产生的轴向变形为

式中，ρi为管内液体密度，kg/m3。

（2）浮力效应

井下深度h处的等效浮力为

浮力产生的轴向应力为

浮力产生的轴向变形为

（3）活塞效应

封隔器由下向上作用的力［3］

封隔器由上向下作用的力

作用于底部球座横截面上的力

其合力为

卡尔曼滤波在线性高斯模型条件下对目标的状态可以进行最优估计,但是实际应用中,系统总是存在不同程度的非线性特征,为了精确估计系统的状态,必须建立适用于非线性系统的滤波算法[14]。所以,本文提出了将EKF与传统二阶软件锁相环相结合的方法,在EKF滤除噪声且捕获有用信号的基础上通过二阶锁相环获取理想的信号频率。

活塞效应产生的轴向变形为

式中，FP为活塞效应力，N；pi为封隔器处管内压力，N；po为封隔器处环空压力，N；p为坐封时的井口压力，N；Ai为管柱内截面积，m2；Ao为管柱外截面积，m2；Ap为封隔器密封腔横截面积，m2。

（4）膨胀效应

根据弹性力学的Lame公式得［8］

由膨胀效应引起的轴向应力为

膨胀效应产生的轴向变形为式中，σr、σt为管柱横截面任意半径r处的径向应力和切向应力，Pa；pi、po为管柱任意位置的管内压力和管外压力，Pa。

1.5压裂过程管柱轴向变形计算

Calculation of pipestring axial deformation during fracturing

此过程中随着压裂液的注入，压裂管柱的轴向变形受重力效应、浮力效应、温度效应、膨胀效应、活塞效应及摩阻效应的综合影响，另外当有效轴向力大于管柱的屈曲载荷时还将受到屈曲效应。由于封隔器已坐封，作业管柱轴向长度不发生变化，这些动态变化的因素所产生的轴向力作用于封隔器。当轴向力大于封隔器的承载能力时封隔器将失效，因此需对封隔器进行强度校核。

重力效应、浮力效应、膨胀效应、活塞效应动态改变所引起管柱轴向变形的计算与前面一样。重力效应和浮力效应产生的轴向变形随管内外液体的密度变化而改变，膨胀效应和活塞效应按压裂时管内外的最大压力计算。温度效应、摩阻效应和封隔器强度校核的计算模型如下：

（1）温度效应

坐封过程中，随着液体的注入，管柱中的温度分布状态也随之发生变化，此过程中，作业管柱上任一深度h的温度变化为［9］任意微元段管柱上的温度分布温度效应产生的轴向变形式中，K为地温梯度，℃/m；Tg为年平均地表温度，℃；TW为注入液的井口温度，℃；Q为液体注入量，m3/min；Cf为注入液的比热；Kh为岩石热导率；Kk为地层热扩散率。

（2）摩阻效应

注入液与管柱的沿程水头损失为任意截面的压降为任意截面的摩擦力为流体摩阻力引起的轴向应力为流体摩阻力产生的轴向变形为式中，Ff为流体摩阻力，N；v为液体注入速度，m/s；λ为摩阻系数。

2　实例计算Case study

2.1 计算结果

Calculation results

以陈平15-2井水力喷射分段压裂为例，作业过程中的基础数据见表1。

表1　陈平15-2井压裂作业基础数据Table 1 Basic data of fracturing operation in Well Chenping 15-2

结合井深、井斜等原始数据，根据建立的模型，用matlab编制计算软件，将各参数分别代入到不同井深、不同作业工况、不同因素下管柱的轴向变形以及轴向总变形，计算结果见表2、表3。作业管柱的轴向变形见图1、图2。计算的下入过程作业管柱的轴向总伸长为2.1 m。对于3 000～4 000 m管柱下深的井，现场用电磁校深法实测的作业管柱伸长约为1.8～2.37 m［9］，误差在10%之内，该模型计算较为准确。

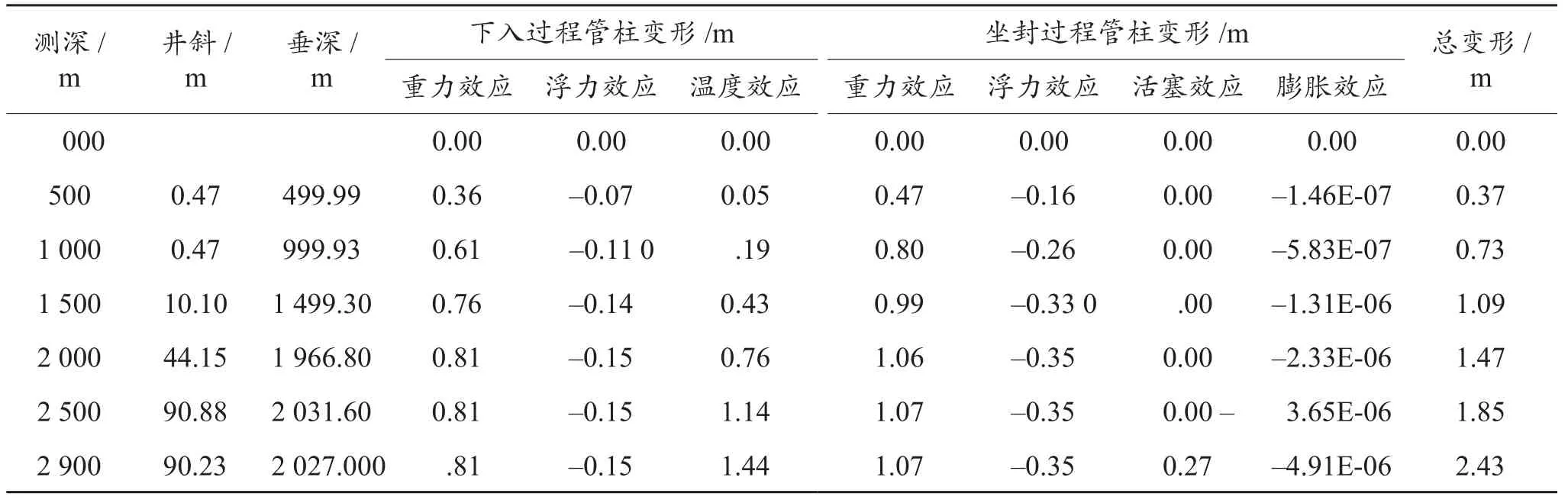
表2　作业管柱真实的轴向变形量Table 2 Actual axial deformation of working pipestring

表3　作业管柱虚构的轴向变形量Table 3 Virtual axial deformation of working pipestring

图1　不同作业过程管柱轴向变形Fig.1 Axial deformation of pipestring in different operational procedures

图2　不同因素下管柱轴向变形Fig.2 Axial deformation of pipestring under different factors

2.2计算结果应用

Application of calculation results

（1）井下作业准确定位。计算出封隔器坐封前管柱的轴向变形（即管柱下入和坐封过程的轴向变形），就可提升或下降作业管柱相应距离，从而准确地对准作业层位。

由表2得陈平15-2井压裂作业中管柱总轴向伸长为2.43 m，实际作业过程中应人为上提作业管柱2.43 m，从而达到更加精确的作业定位。

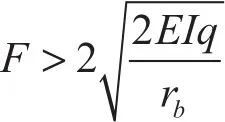
结合表2、表3得压裂过程中本应增加轴向变形ΔL=2.26-2.43= - 0.17 m，所以管柱本应缩短0.17 m，实际上由于封隔器的存在这部分本应缩短的轴向长度将以轴向力的形式作用于封隔器，根据以上计算步骤得F = -14 350.48 N（负号表示管柱受拉力）。陈平15-2井压裂作业所用封隔器为K344-110-Ⅱ型（长胶筒），其承载强度为45 MPa，折合成力为241014 N。F小于其承载能力，可正常作业。

（3）结果分析。结合图1、图2得井下作业管柱的轴向变形与垂深成二次函数关系，而且浮重、温度为主要影响因素，因此，对于深井超深井作业管柱的轴向变形将随着井深增加而成倍增加。

根据计算结果可知，坐封过程中管柱轴向变形达到最大值，此阶段管柱最危险，应用第四强度理论对作业管柱进行强度校核，如强度不满足在管柱组合设计阶段应选择高承载管柱；压裂过程的最大井口压力时，封隔器等作业工具最危险，应根据前文第一步到第三步的方法，对作业工具进行强度校核，如强度不满足根据计算结果增加伸缩补偿器。

3　结论Conclusions

（1）在现有研究的基础之上，严格从作业工况出发，结合井眼轨迹，全面分析了影响压裂管柱轴向变形的因素（重力效应、浮力效应、温度效应、活塞效应、膨胀效应、摩阻效应和屈曲效应）及各因素在不同过程的动态变化，优化了压裂管柱轴向变形的理论计算模型，以具体的水力喷砂压裂为例进行了实例计算，并对计算结果的应用进行了综合分析。

（2）由计算结果得，压裂管柱的轴向变形与测深成二次函数关系，深井超深井管柱的轴向变形将成倍增加；由下入和坐封两过程管柱的轴向伸长量可得作业过程中需要人为的提升距；由坐封后的管柱轴向变形量，结合第四强度理论对作业管柱进行强度校核，判断作业前是否应在管体上加伸缩补偿器以及增加个数；由压裂过程的轴向变形可对作业工具进行强度校核。

［1］ 周楚昌，黄日明.如何应用磁定位曲线校正薄夹层坐封位置［J］. 石油钻采工艺，1990，12（4）：89-90. ZHOU Chuchang， HUANG Riming. How to apply magnetic positioning curve correction thin interlayer packer position ［J］. Oil Drilling & Production Technology， 1990， 12（4）: 89-90.

［2］ 林浩，王铁刚，邓基华. 井眼深度测量及校正［J］. 石油仪器，2005，19（1）：77-78. LIN Hao， WANG Tiegang， DEN Jihua. Borehole depth measurement and calibration［J］.Petroleum Instruments，2005， 19（1）: 77-78.

［3］ 武志学，张晓庆，邱宗斌. 水力喷砂射孔过程中管柱轴向变形及喷点位置分析［J］石油地质与工程，2012，26 （5）：126-127，131. WU Zhixue， ZHANG Xiaoqing， QIU Zongbin. String axial deformation and jetting point position analysisduring hydraulic sand jetting perforation［J］.Petroleum Geology and Engineering， 2012， 26（5）: 126-127， 131.

［4］ 任勇，桂捷，张华光，巨亚锋，付钢旦，马能平.一种准确确定封隔器坐封位置的方法［J］. 石油机械，2007，35 （8）：22-24. RENG Yong， GUI Jie， ZANG Huaguang， JU Yafeng，FU Gangdan， MA Nengping. An method that accurate determining packer position［J］. China Petroleum Machinery， 2007， 35（8）: 22-24.

［5］ 岳欠杯，刘巨保，胡宝华.深井分层压裂管柱受力计算及结果分析［J］. 石油矿场机械，2011，40（8）：23-28. YUE Qianhuai， LIU Jubao， HU Baohua. Force calculation and analysis of gradation frac string in deep well［J］.Oil Field Equipment， 2011， 40（8）: 23-28.

［6］ 李子丰，蔡雨田，李冬梅，徐燕东. 地层测试管柱力学分析［J］. 石油学报，2011，37（4）：709-716. LI Zifen， CAI Yutian， LI Dongmei， XU Yandong. Mechanical analysis of pipe string in formation testing ［J］. Acta Petrolei Sinica， 2011， 37（4）: 709-716.

［7］ 唐海雄，张俊斌，汪顺文，韦红术，高德利，高宝奎. 高温致测试管柱伸长和受力计算分析［J］. 石油机械，2010，38（5）：84-86，91. TANG Haixiong， ZHANG Junbin， WANG Shunwen， WEI Hongshu， GAO Deli， GAO Baokui. Hyperthermia induced elongation and stress calculation analysis of testing string ［J］. China Petroleum Machinery， 2010， 38（5）: 84-86， 91.

［8］ 吕彦平，吴晓东，郭士生，付豪，张国玉.气井油管柱应力与轴向变形分析［J］.天然气工业，2008，28（1）：100-102，172. LV Yanping， WU Xiaodong， GUO Shisheng， FU Hao，ZHANG Guoyu.Tubing string stress and axial deformation in gas well［J］. Gas Industry， 2008， 28（1）: 100-102， 172.

［9］ 崔玉海，唐高峰，丁晓芳，辛林涛，范春宇.注水管柱中温度效应的分析与计算［J］.石油钻采工艺，2003，25（2）：50-54，90. CUI Yuhai， TANG Gaofeng， DING Xiaofang， XIN Lintao，FAN Chunyu. Analysis and calculation of the temperature effect in the water injection string ［J］. Oil Drilling & Production Technology， 2003， 25（2）: 50-54， 90.

［10］ 高德利，刘凤梧，徐秉业. 弯曲井眼中管柱屈曲行为研究［J］. 石油钻采工艺，2000，22（4）：1-4，83. GAO Deli， LIU Fengwu， XU Bingye. Study on the buckling behavior of pipe string in crooked hole［J］. Oil Drilling & Production Technology， 2000， 22（4）: 1-4，83.

［11］ 李子丰，孙虎，苏金柱，徐迎新. 压裂管柱力学分析理论与应用［J］. 应用基础与工程科学学报，2012，20（5）：846-862. LI Zifeng， SUN Hu， SU Jinzhu， XU Yingxin. Theory and applications of mechanical analysis of tubing string in fracturing operation［J］. Journal of Basic Science and Engineering， 2012， 20（5）: 846-862.

（修改稿收到日期 2016-06-24）

〔编辑 薛改珍〕

Theoretical calculation and application of axial deformation in fracturing pipestring

LI Qi1， LI Xuyang1， WANG Zaixing1， ZHANG Yongzhong2
1. College of Petroleum Engineering， Xi’an Shiyou University， Xi’an， Shaanxi 710065， China；2. No.1 Oil Production Plant of Changqing Oilfield Company， Yan’an， Shaanxi 716000， China

Factors affecting axial deformation of pipestring during fracturing have been analyzed. In light of dynamic changes of various factors in field operations， a model for theoretical calculation of axial deformation in fracturing pipestring has been built by using elastic and plastic mechanics and stacking of micro-elements. The newly-developed model was used in calculating the deformation in hydraulic staged fracturing of Well Chenping 15-2. The calculation results show the model can accurately locate downhole operation positions， calibrate strength of various downhole assemblies， and identify required telescopic compensation distance. The relevant research results may provide necessary guidelines for on-site operations.

stress on pipestring； axial deformation； fracturing； operation positioning

TE21

A

1000 - 7393（ 2016 ） 04- 0467- 06

10.13639/j.odpt.2016.04.012

LI Qi， LI Xuyang， WANG Zaixing， ZHANG Yongzhong. Theoretical calculation and application of axial deformation in fracturing pipestring［J］. Oil Drilling & Production Technology， 2016， 38（4）: 467-472， 486.

国家自然科学基金项目“基于多源信息和智能计算的钻井异常自适应预警方法研究”（编号：51574194）资助；陕西省科技工业攻关项目“非常规油气钻井随钻风险动态预警技术研究”（编号：2014K05-02）资助；陕西省教育厅专项科研计划项目“页岩储层地质力学模型的建立方法及应用研究”（编号：16JK1613）。

李琪（1963-），从事石油钻井信息技术、导向钻井等研究，教授，博士生导师。E-mail：liqi@xsyu.edu.cn

李旭阳（1991-），在读硕士研究生。电话：15114878978。通讯地址：（710065）陕西省西安市雁塔区电子二路东段18号。E-mail：619818764@qq.com