国际地磁参考场解算方法及石油工程应用

石在虹滕少臣刘子恒

1. 中国石化石油勘探开发研究院；2. 大庆油田有限责任公司第二采油厂；3. 大庆油田有限责任公司第一采油厂

国际地磁参考场解算方法及石油工程应用

石在虹1滕少臣2刘子恒3

1. 中国石化石油勘探开发研究院；2. 大庆油田有限责任公司第二采油厂；3. 大庆油田有限责任公司第一采油厂

引用格式：石在虹， 滕少臣，刘子恒. 国际地磁参考场解算方法及石油工程应用［J］. 石油钻采工艺，2016，38（4）：409-414.

地磁场包含了从地球内核到宇宙空间的丰富信息，且具有复杂的时空特性及演化规律。国际地磁参考场能较好地描述地磁场的时空分布及变化特征，为石油工程等领域获取地磁数据提供了简洁实用的技术手段。介绍了地磁场特征、地磁场要素和国际地磁参考场，给出了国际地磁参考场的解算方法和步骤，以及在石油工程领域推广应用国际地磁参考场的方法。应用IGRF-12国际地磁参考场，研究了1920～2020年的100年间塔里木盆地地磁场的时空分布及其演化特征，结果表明：塔里木盆地的最大磁偏角为5.98°，最小磁偏角为0.52°，二者相差5.46°。在石油工程应用中，为保证井眼轨迹监测与控制精度，应随时随地更新地磁数据，不能简单地用同一个磁偏角数值来覆盖整个油田或地区，也不能在某个空间位置上长期使用同一个磁偏角数值。

地磁场；石油工程；钻井理论；定向钻井；计算方法

地磁场是地球系统中的一个基本物理场，包含了从地球内核到宇宙空间的丰富信息，是地球科学、航天航空、交通通讯、地震预测等诸多研究领域的基础科学数据。根据地磁场的异常特征预测地质构造及矿产分布已成为一种基本的地球物理勘探方法和手段，广泛应用于金属矿藏和油气藏等资源勘探［1-2］。在石油钻井中，井眼轨迹监测与控制也涉及地磁场问题，其中磁偏角是井眼轨迹归化中不可或缺的基础数据［3-5］。

地磁场具有复杂的时空特性及演化规律。为描述地磁场时空变化特征，世界各国以5～10年为周期，测量、编绘本国的地磁图。自1968年起，国际地磁学与高空物理学协会（IAGA）以各国地磁测量和地磁图为基础，给出了以5年为间隔的国际参考地磁场（International Geomagnetic Reference Field，简称IGRF模型）［6］，并绘制出相应的世界地磁图。针对不同的应用需求，研究者们还建立了多种专用的地磁场模型［7］，如CHAOS模型［8］、EMM模型［9-10］、WDMAM模型［11］等。

地磁场还具有区域性变化特征。全球地磁场模型难以精确描述区域地磁场的空间分布，此外从国家战略的基础资源角度，世界各国都建立了本国的区域地磁场模型［12-13］。从20世纪50年代起，我国也构建了自己的地磁场模型及地磁图，随后每10年进行一次地磁测量和地磁场模型更新［14］。

为满足国内外油气勘探开发需求，基于油气行业广泛采用的IGRF模型，研究了地磁参考场模型及其解算方法，以塔里木盆地为例解析地磁场的分布特征及演化规律，结合油气勘探开发现状给出地磁参考场模型在石油工程中的应用建议。

1　地磁场特征Features of geomagnetic field

地磁场是一个重要的地球物理场，且具有复杂的时空特性及演化规律。地磁场近似于一个置于地心的偶极子磁场。地磁轴与地球自转轴并不重合。地心磁偶极子轴线与地球表面的2个交点称为地磁极，地理北极附近的地磁极称为地磁北极，地理南极附近的地磁极称为地磁南极。地磁北极和地磁南极指的是地理位置。按磁性来说，地磁两极和磁针两极的极性恰好相反。地磁偶极子的磁矩方向，如图1所示。

图1　地心偶极子磁场Fig.1 Dipole magnetic field in Earth’s core

地磁场是由地球内部的磁性岩石以及分布在地球内部和外部的电流体系所产生的各种磁场成分叠加而成。按场源位置划分，地磁场可分为内源场和外源场［15-17］。内源场起源于地表以下的磁性物质和电流，可分为地核场和地壳场。地核场又称主磁场，由地核磁流体发电机过程产生的。地壳场又称局部异常磁场，由地壳磁性岩石产生的。主磁场和局部异常磁场变化缓慢，所以又合称为稳定磁场。外源场起源于地表以上的空间电流体系，主要分布在电离层、磁层和行星际空间。由于这些电流体系随时间变化较快，所以外源磁场通常又称变化磁场。从全球来看，地核主磁场占总磁场95%以上，局部异常磁场约占4%，外源变化磁场只占总磁场1%。由此可见，稳定磁场是地磁场的主要组成部分，占总磁场99%以上，也称为基本磁场［15-17］。

地磁场是矢量场，是空间位置和时间的函数。如图2所示。为了描述地磁场的空间分布，可建立直角坐标系O—NEH，其中N轴指向地理北，E轴指向地理东，H轴铅垂向下。习惯上，总磁场强度用F表示，在3个坐标轴上的分量分别记为X、Y和Z。此外，常用的地磁场要素还有：水平强度U，是地磁场矢量的水平分量，指向磁北极方向；磁偏角δ，是水平分量U偏离地理北向的角度，也是磁子午线与真子午线之间的夹角。从真子午线起算，磁偏角东偏时为正，西偏时为负；磁倾角β，是地磁场矢量与水平面之间的夹角。磁倾角下倾时为正，上倾时为负［15-17］。

图2　地磁场要素Fig.2 Key elements of the geomagnetic field

地磁场要素之间存在如下关系

式中，F为磁场强度，nT；U为磁场水平强度，nT；X、Y、Z分别为磁场强度在北方向、东方向、垂深方向的分量，nT；δ为磁偏角，（°）；β为磁倾角，（°）。

2　地磁参考场模型Model of geomagnetic reference field

1839年高斯提出了地磁场的球谐分析方法，1885年施密特把地磁要素的地面分布表示成了地理坐标的数学函数，为从理论上解决地磁场的成因问题奠定了基础。自1968年以来，国际地磁和高空物理协会（IAGA）基于高斯—施密特理论，每5年给出一套全球性的国际地磁参考场（IGRF）。国际地磁参考场的误差大约为100 nT，个别地方达到200 nT。

IGRF模型采用球谐分析方法来描述地磁场。在地心直角坐标系下，地磁场分量表示为

式中，a为地磁参考半径（取地球平均半径，即a = 6 371.2 km），m；r为离开地心的径向距离，m；λ为东经，（°）；θ为地心余纬度，（°）；和为高斯球谐系数，nT；（cosθ）为n阶m次施密特型缔合勒让德函数；N为最高阶数。

目前，最新的国际地磁参考场是IGRF-12，其球谐系数高达13阶［18］。IGRF模型的球谐系数有DGRF和IGRF 2种方式：DGRF是确定型数据，当更新数据时不再修改；而IGRF及SV（长期变化）是非确定型数据，当再次更新数据时会被修改。

3　地磁参考场的解算方法Algorithm for the geomagnetic reference field

应用IGRF模型解算地磁场空间分布的总体思路是：首先由式（4）计算出地磁场分量（x，y，z），然后将其转换为直角坐标系O—NEH下的地磁场分量（X，Y，Z），便可由式（1）和式（2）计算出其他地磁场要素，从而得到地球表面及向外空间任一点和任一时刻的正常地磁场［18-22］。具体方法如下：

（1）给定空间位置和计算时刻。空间位置数据包括东经度L、纬度B和高程h。计算时刻t以年为单位，且应考虑闰年情况。

（2）将大地坐标（h，L，B）转换为地心坐标（r，λ，θ）。

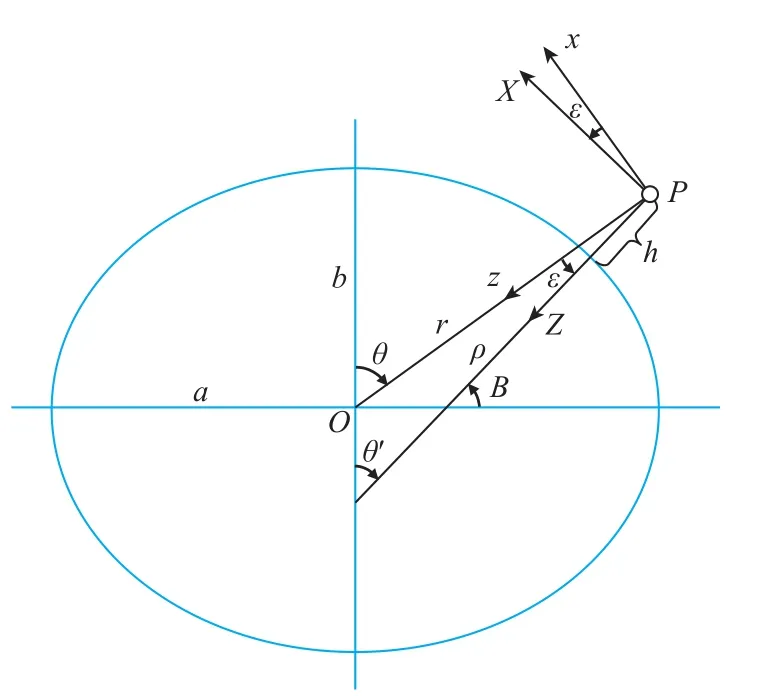
图3　地心坐标系下的地磁场分量Fig.3 Components of geomagnetic field under geocentric coordinate system

由于地磁场模型是根据参考圆球导出的，所以要将大地坐标转换为地心坐标才能使用地磁场模型来计算地磁场分量。如图3所示。地心坐标系的经度λ与大地坐标系的经度L相等，径向距离r的计算方法为

式中，θ'为大地余纬度，（°）；a为地球椭球的长半径，m；b为地球椭球的短半径，m。通常，地球椭球采用WGS-84椭球，故取a2=40 680 631.59 km2，b2= 40 408 299.98 km2。

地心余纬度θ的计算公式为

其中

（3）计算即时球谐系数

（4）缔合勒让德函数。为便于计算，常用递推公式来求取缔合勒让德函数及其导数。根据缔合勒让德函数的定义，可得到如下递推关系

其中

式（9）和式（10）适用于n ＞ 1的情况。

（5）计算地磁场要素。首先按式（4）计算地心坐标系下的地磁场分量（x，y，z），然后转换为直角坐标系O—NEH下的地磁场分量（X，Y，Z）。即

最后，按式（1）和式（2）计算其他的地磁要素。

4　塔里木盆地的地磁场模拟Simulation of geomagnetic field in the Tarim Basin

塔里木盆地东西长约1 500 km，南北宽约600 km，海拔高度为800～1 300 m，富含石油天然气资源。若取高程h=1 000 m、计算时刻t为2016年8月12日，根据IGRF-12国际地磁参考场，按上述地磁参考场的解算方法可得到塔里木盆地的地磁场分布（见图4）。

图4　塔里木盆地的地磁场分布Fig.4 Distribution of geomagnetic field in the Tarim Basin

磁偏角是井眼轨迹方位角及坐标归化中的一项基础数据。在上述计算条件下，逐年模拟了1920-2020年100年间塔里木盆地的磁偏角分布及其变化规律。其中，部分时刻的磁偏角分布见图5，塔里木盆地4个顶点及中心点的磁偏角变化规律见图6。

模拟结果表明，在1920-2020年的100年间，塔里木盆地的磁偏角及其变化规律有以下特点：（1）最大磁偏角为5.98°（经度L=76°，纬度B=42°，时刻t=1920），最小磁偏角为0.52°（经度L=90°，纬度B=36°，时刻t=1965），二者相差5.46°；（2）在1920-1980的60年间，塔里木盆地西北角（经度L=76°，纬度B=42°）的磁偏角波动幅度超过1.92°；（3）在1922-1923年间，塔里木盆地东北角（经度L=90°，纬度B=42°）的磁偏角变化（相当于年变化率）接近0.09°。

图6　磁偏角随时间的变化规律Fig.6 Variation pattern of declination with time

上述模拟结果展示了塔里木盆地不同地点和不同时间的地磁场变化情况，结果表明：地磁场随地点和时间均有明显变化。因此，在石油物探、定向钻井等石油工程领域应考虑地磁场的时空演化特性，不能简单地用同一个地磁数据来覆盖整个油田或地区，也不能在某个空间位置上长期使用同一个地磁数据。例如，在定向钻井过程中，通常采用真北或网格北（即地图投影平面纵坐标北）作为指北基准，而通过MWD等测量仪器所获取的方位角多为磁方位角。因此，应考虑此时此地的磁偏角等参数，先将磁方位角归算为真方位角或网格方位角，然后再计算北坐标、东坐标等井眼轨迹参数，才能将井眼轨迹归算到所选定的坐标系下，进而实施井眼轨迹监测与控制。

5　结论Conclusions

（1） 稳定的地磁场占总磁场99%以上，因此国际地磁参考场的模拟精度可以满足石油工程需求，且具有5年更新、全球适用等优点。

（2） 应用国际地磁参考场能计算磁偏角等地磁要素，为石油工程获取基础数据提供了简洁实用的技术手段。

（3） 地磁场随时间和地点变化，不能简单地用同一个地磁数据来覆盖整个油田或地区，也不能在某个空间位置上长期使用同一个地磁数据，应随时随地更新地磁数据。

（4） 在石油工程应用中，及时更新地磁数据是保证井眼轨迹监测及控制精度的基础。给出国际地磁参考场的具体解算方法，便于推广应用国际地磁参考场。

［1］ 李世峰，金瞰昆，周俊杰. 资源与工程地球物理勘探［M］. 北京：化学工业出版社，2008. LI Shifeng， JIN Kankun， ZHOU Junjie. Resources and engineering geophysical exploration ［M］. Beijing: Chemical Industry Press， 2008.

［2］ 李才明，李军. 重磁勘探原理与方法 ［M］. 北京：科学出版社，2013. LI Caiming， LI Jun. Gravity and magnetic prospecting principle and method ［M］. Beijing: Science Press， 2013.

［3］ SY/T5435—2012. 定向井轨道设计与轨迹计算 ［S］. 2012-08-23. SY/T5435—2012. Wellpath planning & trajectory calculation for directional wells ［S］. 2012-08-23.

［4］ 刘修善. 井眼轨道几何学 ［M］. 北京：石油工业出版社，2006. LIU Xiushan. Geometry of wellbore trajectory ［M］. Beijing: Petroleum Industry Press， 2006.

［5］ 刘修善. 定向钻井中方位角及其坐标的归化问题 ［J］.石油钻采工艺，2007，29（4）：1-5. LIU Xiushan. Naturalization of azimuth angles and coordinates in directional drilling ［J］. Oil Drilling & Production Technology， 2007， 29（4）: 1-5.

［6］ IAGA， Working Group V-MOD. Internationalgeomagnetic reference field: the eleventh generation ［J］. Geophys. J. Int.， 2010， 183（3）: 1216-1230.

［7］ 徐如刚，顾左文，黎哲君，谈昕，张毅，王雷，袁洁浩，翟洪涛，辛长江，苏树鹏. 2005-2010年中国地磁测量与地磁场模型的应用 ［J］. 地球物理学进展，2014，29（5）：2092-2099. XU Rugang， GU Zuowen， LI Zhejun， TAN Xin， ZHANG Yi， WANG Lei， YUAN Jiehao， ZHAI Hongtao， XIN Changjiang， SU Shupeng. Application of Chinese geomagnetic survey and geomagnetic model for 2005-2010 ［J］. Progress in Geophysics， 2014， 29（5）: 2092-2099.

［8］ MAUS S， ROTHER M， STOLLE C， MAI W， CHOI S，LÜHR， H. Third generation of the Potsdam magnetic model of the earth （POMME） ［J］. Geochemistry Geophysics Geosystems， 2006， 7（7）: 295-295.

［9］ LANGLAIS B， MANDEA M， ULTRÉ-GUÉRARD P. High-resolution magnetic field modeling: application to MAGSAT and šrsted data ［J］. Physics of the Earth and Planetary Interiors， 2003， 135（2-3）: 77-91.

［10］ PURUCKER M E. Magnetic anomaly map of the world ［J］. Eos Transactions American Geophysical Union，2007， 88（25）: 263.

［11］ HEMANT K， THÉBAULT E， MANDEA M， RAVAT D，MAUS S. Magnetic anomaly map of the world: merging satellite， airborne， marine and ground-based magnetic data sets ［J］. Earth & Planetary Science Letters， 2007，260（1-2）: 56-71.

［12］ 安振昌. 区域和全球地磁场模型 ［J］. 地球物理学进展，1995，10（3）：63-73. AN Zhenchang. Regional and global geomagnetic field models ［J］. Progress in Geophysics， 1995， 10（3）: 63-73.

［13］ 王亶文. 地磁场模型研究 ［J］. 国际地震动态，2001，（4）：1-4. WANG Tanwen. Research on geomagnetic field model ［J］. Recent Developments in World Seismology， 2001，（4）: 1-4.

［14］ XU Wenyao， XIA Guohui， AN Zhenchang， CHEN Gengxiong， ZHANG Fengyu， WANG Yuehua， TIAN Yugang， WEI Zigang， MA Shizhuang， CHEN Hongfei. Magnetic survey and ChinaGRF 2000［J］. Earth Planets Space， 2003， 55（4）: 215-217.

［15］ 北京大学地球物理教研室，中国科学技术大学地球物理教研室. 地磁学教程 ［M］. 北京：地震出版社，1986. Earth physics teaching and research section of Beijing University， Earth physics teaching and research section of university of science and technology of China. Geomagnetism course ［M］. Beijing: Seismological Press， 1986.

［16］ 丁鉴海，卢振业，黄雪香. 地震地磁学 ［M］. 北京：地震出版社，1994. DING Jianhai， LU Zhenye， HUANG Xuexiang. Earthquake geomagnetism ［M］. Beijing: Seismological Press， 1994.

［17］ 徐文耀. 地磁学 ［M］. 北京：地震出版社，2003. XU Wenyao. Geomagnetism ［M］. Beijing: Seismological Press， 2003.

［18］ IAGA， Working Group V-MOD. International geomagnetic reference field［OL］. ［2014-12-22］. http: //www.ngdc.noaa.gov/ IAGA/vmod/igrf.html.

［19］ 柴松均，陈曙东，张爽. 国际地磁参考场的计算与软件实现 ［J］. 吉林大学学报：信息科学版，2015，33（3）：280-285. CHAI Songjun， CHEN Shudong， ZHANG Shuang. Calculation and software realization of international geomagnetic reference field ［J］. Journal of Jilin University: Information Science Edition， 2015， 33（3）: 280-285.

［20］ 刘元元，王仕成，张金生，郑玉航，乔玉坤. 最新国际地磁参考场模型IGRF11研究 ［J］. 地震学报，2013，35 （1）：125-134. LIU Yuanyuan， WANG Shicheng， ZHANG Jinsheng，ZHENG Yuhang， QIAO Yukun. Research on the eleventh generation IGRF ［J］. Acta Seismologica Sinica， 2013，35（1）: 125-134.

［21］ 毛玉仙. 国际地磁参考场的计算 ［J］. 铀矿地质，1992，8（1）：48-52. MAO Yuxian. The calculation of the international geomagnetic reference field ［J］. Uranium Geology，1992， 8（1）: 48-52.

［22］ 高德章. 国际地磁参考场及其计算 ［J］. 海洋石油，1999，19（3）：34-42. GAO Dezhang. International geomagnetic reference field & computation ［J］. Offshore Oil， 1999， 19（3）: 34-42.

（修改稿收到日期 2016-06-20）

〔编辑 薛改珍〕

Algorithm for international geomagnetic reference field and its application in petroleum engineering

SHI Zaihong1， TENG Shaochen2， LIU Ziheng3
1. SINOPEC Petroleum Exploration & Production Research Institute， Beijing 100083， China；2. No.2 Oil Production Plant， CNPC Daqing Oilfield Limited Company， Daqing， Heilongjiang 163414， China；3. No.1 Oil Production Plant， CNPC Daqing Oilfield Limited Company， Daqing， Heilongjiang 163000， China

Geomagnetic field contains rich information from inner core the earth to the universe， and has complicated time-space features and evolution patterns. The international geomagnetic reference field （IGRF） can satisfactorily reflect time-space distribution and changes of the geomagnetic field， and provide petroleum engineering with a simple and practical technical measure to obtain geomagnetic data. This paper reviewed features and key elements of geomagnetic field， and IGRF. Algorithm and procedures for IGRF have been proposed to promote application of IGRF in petroleum engineering. The IGRF-12 has been used to study time-space distribution and evolution pattern of geomagnetic field in the Tarim Basin over 100 years from 1920 to 2020. The research results show that the Tarim Basin has a maximum declination of 5.98°， minimum declination of 0.52°， and a difference of 5.46° between the two. In petroleum engineering， geomagnetic data need to be updated timely to ensure accurate monitoring and control over borehole trajectory. It is not proper to use the same declination value to cover the entire oilfield or the region， or use the same declination value for certain spatial position over a long time.

geomagnetic field； petroleum engineering； drilling theory； directional drilling； computing method

TE243

A

1000 - 7393（ 2016 ） 04- 0409- 06

10.13639/j.odpt.2016.04.001

SHI Zaihong， TENG Shaochen， LIU Ziheng. Algorithm for international geomagnetic reference field and its application in petroleum engineering［J］. Oil Drilling & Production Technology， 2016， 38（4）: 409-414.

石在虹（1963-），教授级高级工程师，主要从事采油工艺技术研究工作。通讯地址：（100083）北京市海淀区北四环中路267号奥运大厦。E-mail：shizaihong.syky@sinopec.com