基于双向A*算法的城市无人机航路规划

林　娜，李天啸

(沈阳航空航天大学 计算机学院，沈阳 110136)



基于双向A*算法的城市无人机航路规划

林娜，李天啸

(沈阳航空航天大学 计算机学院，沈阳 110136)

应用双向A*算法对在城市环境中的无人机进行航路规划，对比传统的A*搜索算法，双向A*搜索算法提高了搜索的效率，大大缩短了航路规划的时间。同时针对双向A*算法现有的不足，对双向A*算法进行改进，提出了同步双向A*搜索算法思想，通过编程实现双向A*算法正向搜索和反向搜索同步进行，并且采用栅格法对无人机的飞行环境进行建模，在建模时充分考虑城市环境确定栅格的大小。通过实验验证，同步双向A*算法可以快速为无人机规划出航路，且航路可飞，对比改进前的双向A*算法，同步双向A*算法的航路规划速度更快，效率更高。

无人机；双向A*；栅格法；城市环境；航路规划

A*算法是一种经典的启发式搜索算法，并广泛应用于路径搜索问题中。A*算法的思想最早由P.E Hait和N.J Nilsson提出，在以后的应用中得到了不断的改进与发展。如：J.Szczerba提出了稀疏A*算法(Sparse A*Search，SAS)[1]，其主要思想为通过一个约束函数将A*算法的搜索范围缩小，缩短了算法的时间，提高了算法的搜索效率；何雨枫、曾庆化等提出了无记忆A*算法[2]的思想，针对A*算法的OPEN表和CLOSE表进行改进，使OPEN表中的节点数每次都保持最小，从而提高算法的计算速度。

而以上方法都是基于单一方向的A*算法，即从起始节点向目标节点搜索。而本文将应用双向A*算法对无人机的航路进行搜索，并针对传统双向A*算法存在的不足，提出了同步双向启发式A*算法，将其应用于栅格建模环境中。

栅格思想由M．B．Meteas提出[3]，而A*算法便是基于栅格空间的一个经典的路径规划算法。应用同步双向启发式A*算法，通过把约束条件结合到搜索算法中去，可以有效地修剪搜索空间中无效的节点，从而缩短搜索时间，而同步双向启发式A*算法的应用，可以提高路径搜索的效率，缩短路径搜索的时间。通过实验表明，该算法可行。

1　问题描述与环境建模

1.1问题描述

近年来，随着无人机技术的不断成熟与发展，无人机不再只局限于军事领域之中，在民用领域中，诸如交通监测、事故调查、追踪车辆等任务中，无人机以其机动性高、受环境影响小、反应迅速、低空飞行等特点，在执行任务时有着得天独厚的优势。然而在执行这些任务时，无人机的飞行环境大多以城市为主，而在城市环境中，对无人机来说最主要的障碍物就是城市中的建筑物。当无人机进行超低空飞行时，可以将每个街区近似看成一个大的障碍物，而这些障碍物相对于无人机来说都是静止的，对路径规划来说也是已知的。

无人机从给定的起始点出发，最终要到达位置已知的目标点，在障碍物位置与高度已知的条件下，通过路径规划，使无人机可以避开障碍物，为无人机规划出一条适合城市环境的飞行航路。

1.2环境建模

本文将应用栅格思想对无人机的飞行环境进行建模。将无人机飞行的城市环境按栅格法分解成若干个栅格，栅格的大小按城市的规模而定。如果城市规模特大，栅格的大小也可按区域划分。栅格的大小直接影响搜索算法的搜索效率：栅格越小，环境表达越精细，信息量越大，搜索算法的负担就会越重，效率会下降；而较大的栅格会导致环境表达粗糙，使规划出的航路不够精细。

将每个栅格的中心点看作是A*算法的一个备选节点，若一个栅格内包含障碍物，则将其视为障碍节点；若栅格空间内不包含障碍物，则将其视为自由节点。

目前，无人机可分为固定翼无人机和旋翼无人机两大种类，旋翼无人机相比于固定翼无人机来说，其机动性及其可悬停性更适合在城市环境中飞行和执行任务。

对于旋翼无人机来说，由于其机动性很强，转弯不受转弯角度和转弯半径的限制，所以以旋翼无人机所在栅格为中心，周围的上下左右8个栅格均为其可机动栅格，如图1所示。

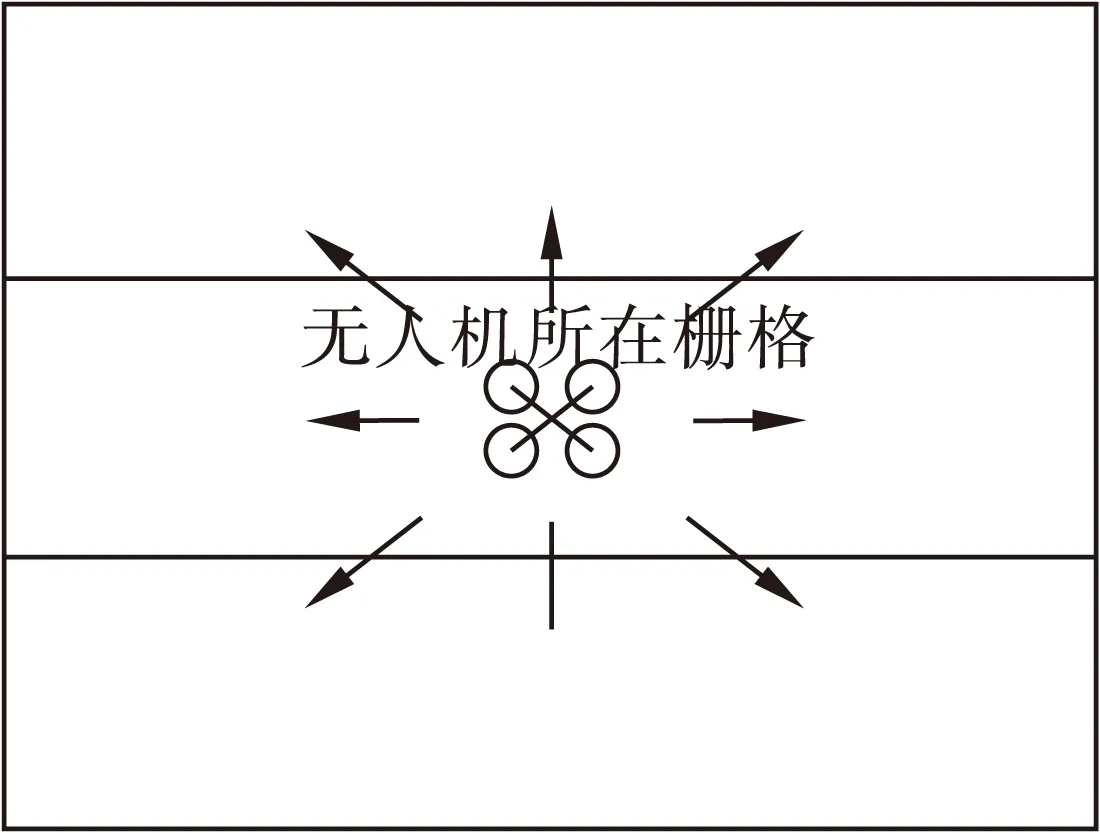
图1　旋翼无人机可机动栅格示意图

旋翼无人机由于其机动性强的特性，在设计栅格大小的时候就可以不用考虑无人机转弯角度和转弯半径等因素。可以更多地考虑所在城市的具体环境，如街区的尺寸和建筑物的尺寸等因素，使设计出的栅格模型更符合每个城市的特点，为无人机规划出精细的航路的同时，也不会为搜索算法带来太多的负担。

2　基于双向A*搜索算法的无人机航迹规划

2.1任务条件描述

城市环境信息完全已知，所以问题可以简化为在静态环境中寻找从起始点到目标点的最优无障碍路径的经典全局路径规划问题。

根据已知障碍分布与地形，对无人机从起始点到目标点之间的距离进行航路预规划，针对航路规划要求日趋快速精确的特点，传统的A*搜索算法已经不能满足性能要求，所以需要针对传统的A*搜索算法进行改进，提高其航路规划的效率。

2.2双向A*搜索算法

所谓双向A*搜索算法，指的就是搜索沿着正反两个方向同时进行，如图2所示：

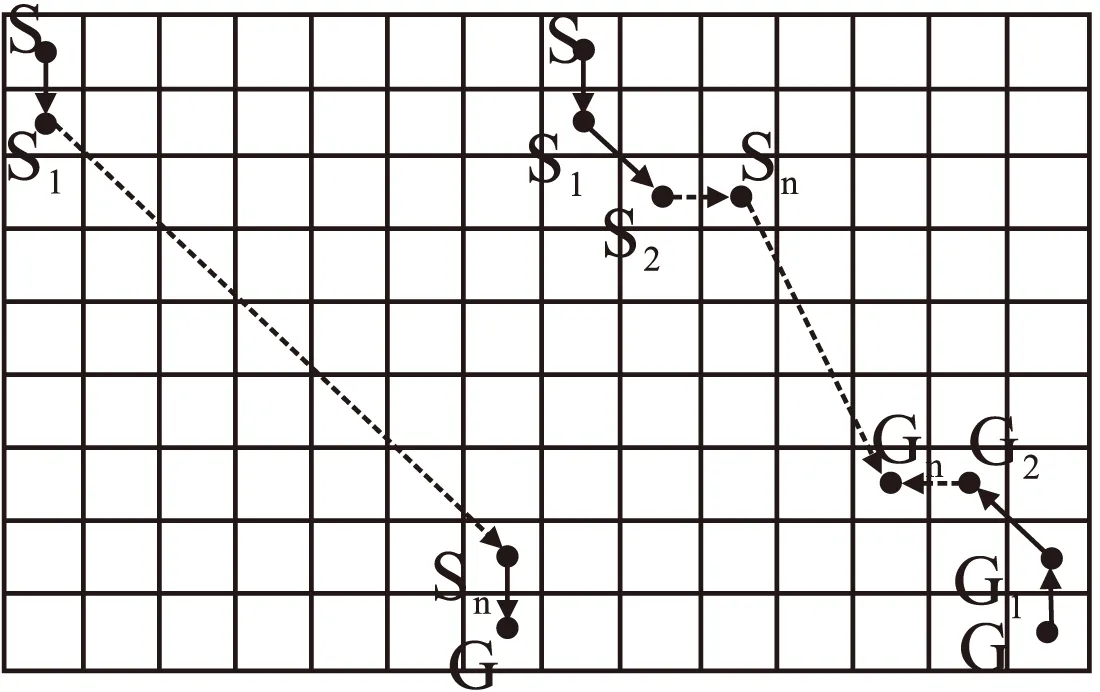
图2　双向搜索示意图

正向搜索是指从起始点方向向目标点方向搜索，而反向搜索则是指从目标点方向向起始点方向进行搜索。在搜索过程中，要把另外一个方向上已经产生的节点作为现节点的目标节点。如图，在正向搜索过程中，将反向搜索的当前点G2作为正向搜索的目标节点，相对的，在反向搜索过程中，将正向搜索的当前节点S2作为反向搜索的目标节点。正向和反向搜索过程同时进行。

当正向和反向搜索同时将一个节点作为目标节点(如图节点为Sn或Gn)，且该节点满足两个方向搜索的约束条件，则搜索结束。

2.3对双向A*搜索算法的改进

在双向启发式A*算法中，有两个条件是必不可少的，一个是算法停止搜索的条件，另一个是正向搜索和反向搜索之间转换的条件。

在算法终止的条件中，如上图所示，当正向搜索和反向搜索的目标节点为同一个节点时，且该节点满足两个方向搜索的约束条件，则路径搜索成功，搜索算法终止。

另一种情况(如图3所示)，当正向搜索和反向搜索的目标节点没有相遇，而是分别搜索到了自己方向上的目标节点，或者两个方向在搜索过程中一直在更新目标节点，而目标节点一直没有相遇陷入循环的情况下，将终止搜索算法，作为搜索失败处理，在这种情况下，只选择正向搜索出来的路径选为全局路径。

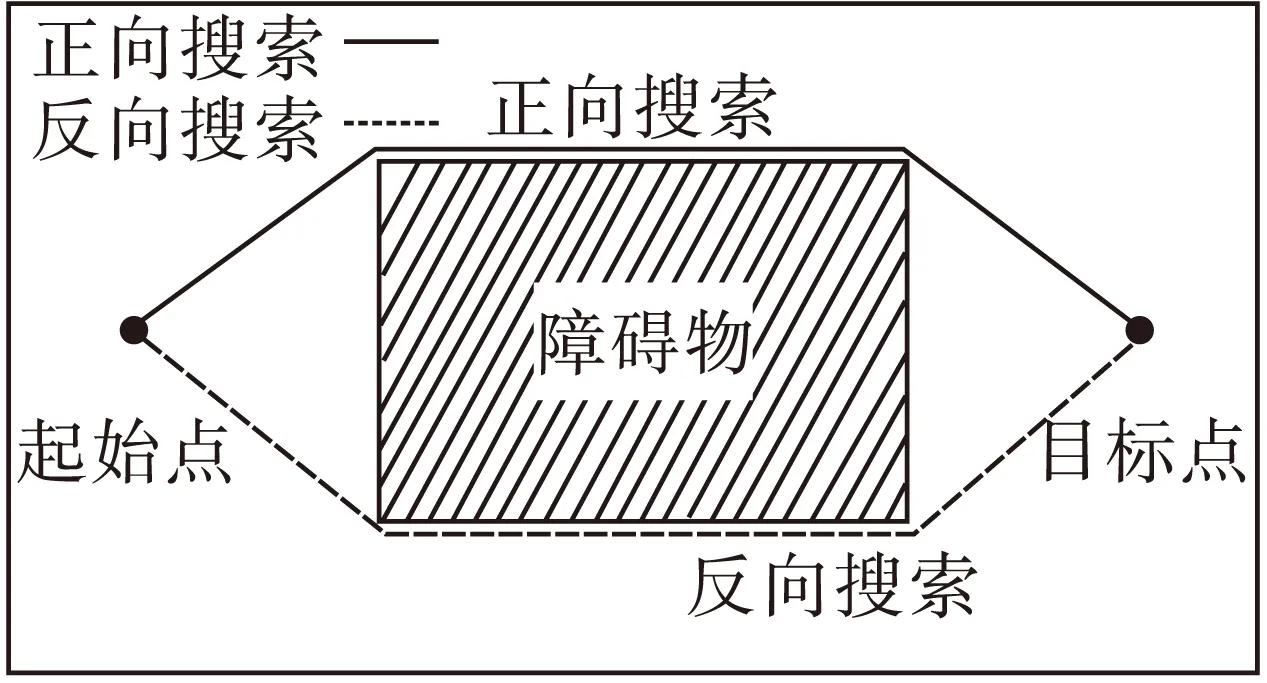
图3　特殊情况算法搜索示意图

理想的条件下，正向搜索和反向搜索会在起始节点和目标节点连线的中心点相遇，这样在理想状态下，可以减少一半的搜索空间(如图4所示)，但是在实际的无人机飞行环境中，会有不同的障碍阻挡在航路之中，正向搜索和反向搜索往往不会在起始点和目标点的中心相遇，而在极端情况下，可能会比单向A*搜索的代价还要大，所以要保证搜索在中间部分相遇，而避免在边缘区域相遇。

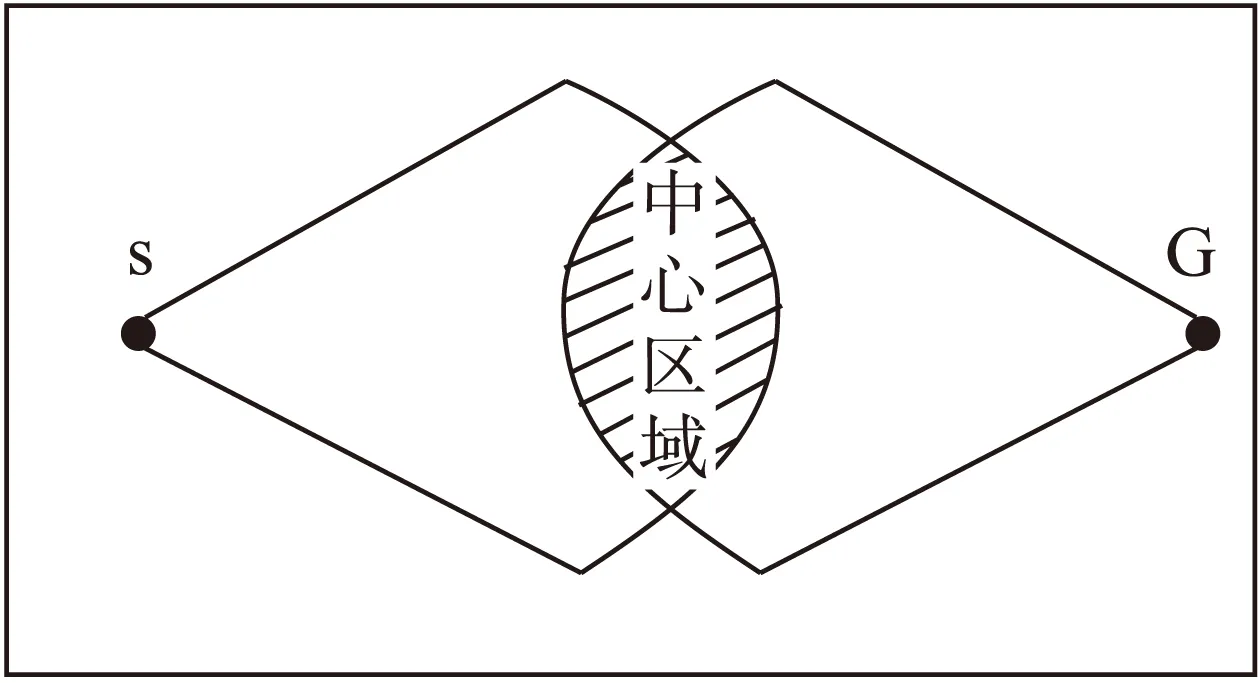
图4　双向搜索相遇区域示意图

传统的双向A*搜索算法在搜索过程中，正向搜索和反向搜索是交替进行的。也就是说，先进行一次正向搜索，当正向搜索搜索到一个代价最小的节点时，再进行反向搜索，且反向搜索将正向搜索到的当前最佳节点作为目标节点进行搜索。

这里对正向搜索与反向搜索交替进行的机制进行改进，改进的目的是使双向A*算法的正向搜索和反向搜索同时进行，提出同步双向A*搜索算法的思想。

在改进之后，因为正向和反向搜索是同步进行的(如图5所示)，所以两个方向上的搜索就不能将对向的当前节点作为目标节点，为了保证算法在搜索过程中保持同步且在正向与反向搜索的中心区域相遇，规定将两个方向上当前节点的前一个节点作为两个方向搜索的目标节点。如图2所示，在进行搜索时，正向搜索的当前节点S2是以反向搜索中节点G1作为目标节点搜索得来的，反向搜索的当前节点G2则是以正向搜索中节点S1作为目标节点搜索得来的，这样可以保证两个方向上搜索的目标节点同时更新，即保证了正反两个方向的搜索可同时进行。

具体步骤如下：

Step1：将两个方向上的起始节点分别放入OPEN0表和OPEN1表。

Step2：判断OPEN0表和OPEN1表是否为空，若为空，则搜索失败，退出。

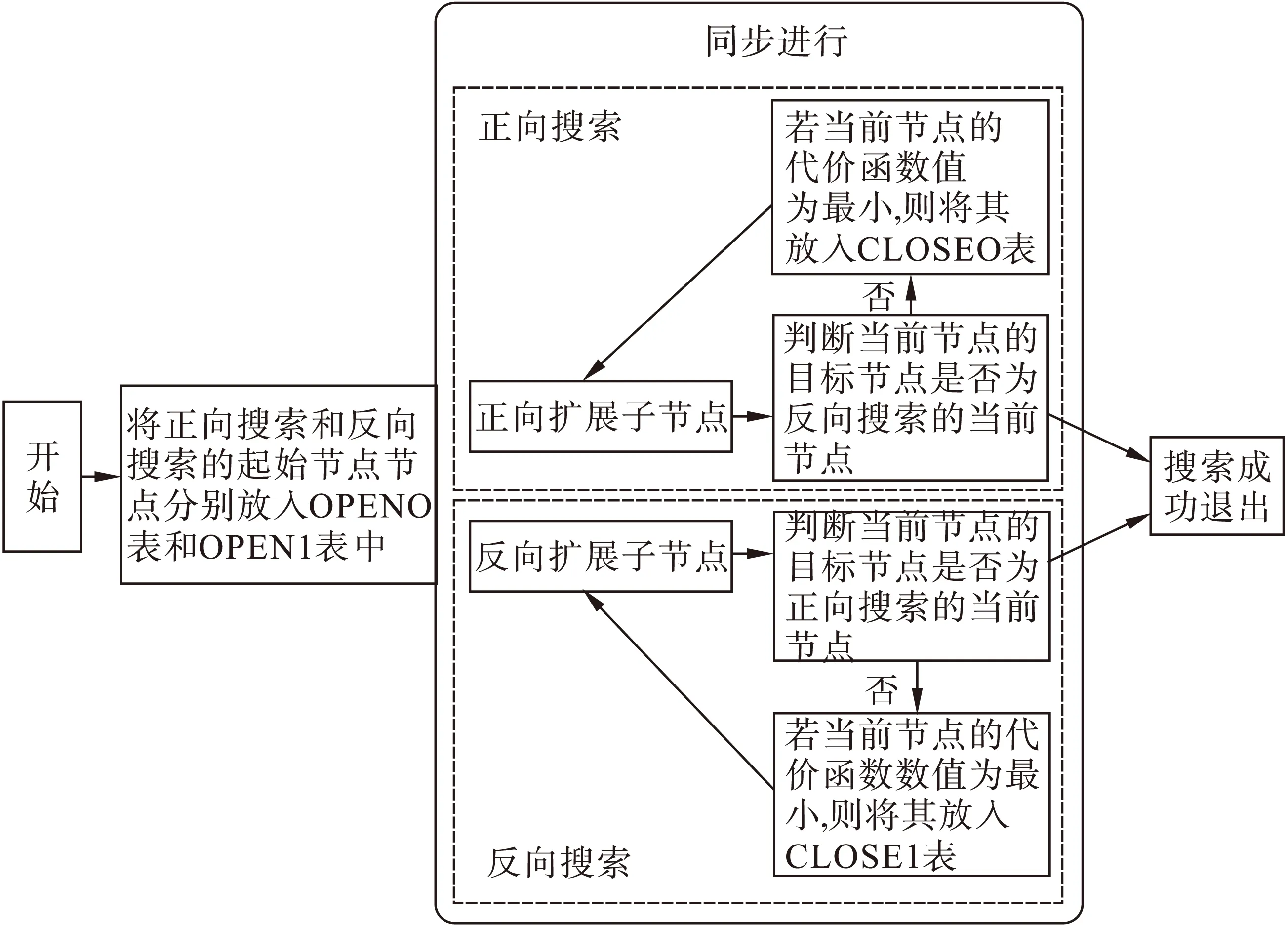
图5　同步双向A*搜索过程示意图

Step3：移出OPEN0表和OPEN1表中的第一个节点，放入CLOSE0表和CLOSE1表中。

Step4：若当前节点的目标节点为相对方向上搜索的当前节点，则搜索成功，退出。

Step5：若OPEN表中的当前节点不能再扩展，转Step2。

Step6：扩展当前节点邻域上的子节点，对比子节点的代价函数值，确定下一个扩展节点，将余下的待选节点放入OPEN0表和OPEN1表中，转Step2。

3　代价评估函数

在航路规划的过程中，代价评估函数是其中的核心问题也是难点，一个好的代价评估函数应该具有以下特点：计算简单，不能有太大的计算量，否则会影响算法的性能；直观明了，对航迹中代价评估客观真实，函数中各个变量意义明确。

该算法的代价评估函数如式(1)所示：

f(n)=g(n)+h(n)

(1)

公式中：f(n)为待选节点的评价函数，g(n)为从起始点到节点n的代价，h(n)为从节点n到目标点的启发式估值，h(n)的设计对A*算法能否找到可行解以及算法的求解速度和性能起到了决定性的作用。一个好的h(n)应该满足小于并且尽量接近于真实值。

因为在城市中，无人机的飞行环境相对稳定，只需要避开建筑物和一些特殊敏感区域如军事部队驻地上空和机场周边空域即可。这里选取欧几里得距离作为评价函数的计算方法，即起点到任意节点的代价值为其父节点的代价值加上该节点与父节点之间的距离，任意节点到目标节点的启发式估值为该节点到目标节点的直线距离。

用n表示待选节点，m表示其父节点，即当前正在扩展的节点，g(n)和h(n)的计算分别如式(2)和式(3)所示：

(2)

(3)

式中，g(m)为从起始点到节点m的代价值，nx、ny为待选节点的坐标值，mx、my为当前节点的坐标值，goalx、goaly为目标节点的坐标值。

反向搜索中采用与正向搜索相同的代价评估函数。在两个方向上应用相同的代价评估函数，确保正反两个方向上的搜索效率相同，使两个方向同时更新目标节点，保证正向搜索和反向搜索可以同步进行。

4　结果分析

采用同步双向A*搜索算法对无人机进行航路规划仿真，并与单向A*搜索算法和传统双向A*搜索算法进行对比。实验计算机为Windows7 x64操作系统，处理器主频为3.10 GHz。

实验过程中，引入障碍物、建筑物以及禁飞空域，且障碍物的位置可以在每次规划之前即时更新。

以下是同步双向A*搜索算法进行航路搜索的程序运行截图：

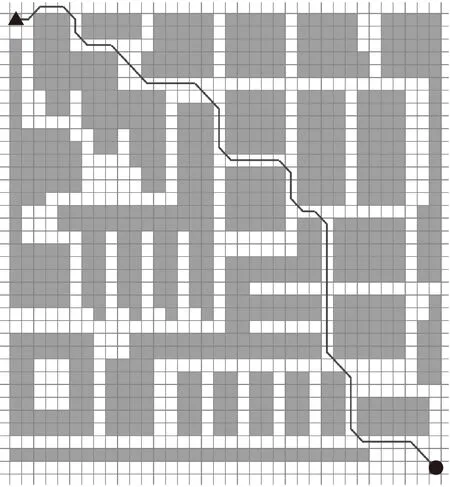
图6　搜索案例一

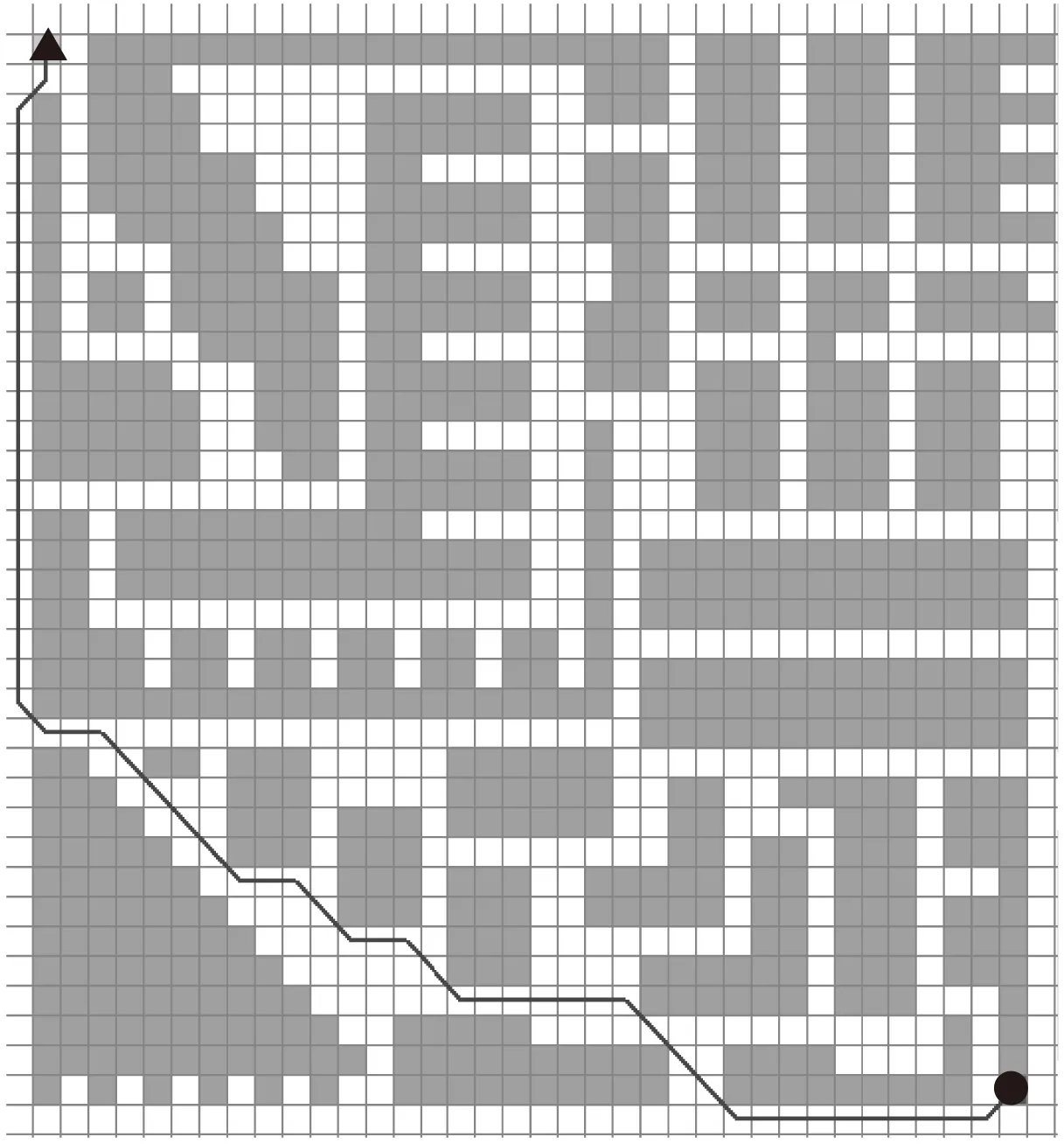
图7　搜索案例二

其中黑色三角形代表起始点，黑色圆形代表目标点，灰色阴影部分代表障碍物。图6和图7说明，程序在不同的城市环境下可以为无人机快速规划出航路，且航路可飞。

图8说明在起始点与目标点之间障碍物对称的情况下，同步双向A*算法也可为无人机规划出代价较小航路，并没有陷入循环状态，且规划出的航路可飞。

表1是单向A*搜索算法、双向A*搜索算法与同步双向A*搜索算法在相同条件下对航路进行规划的用时和航路距离的对比。距离的单位为栅格，航路长度62表示无人机从起始点到目标点经过了62个栅格，时间单位为秒。起始点分别设定在栅格环境的左上角、右下角和中间位置，对应的目标点分别选在起始点的上方、两侧与对角位置。当目标点更换时，障碍物保持不变的情况下，对三种算法进行横向比较。从表中的数据可以看出，在航路规划的距离上，三种算法是相同的，说明双向A*搜索算法可以得到与单向A*搜索算法相同的最优解。而在航路规划的时间上，双向A*搜索算法则比传统的单向A*搜索算法缩短了近一半的时间，而改进后的同步双向A*搜索算法，对比传统的双向A*搜索算法在航路规划的用时上又有所缩短，这表明在双向搜索中，正向搜索与反向搜索同步进行，可以提高算法的搜索效率。

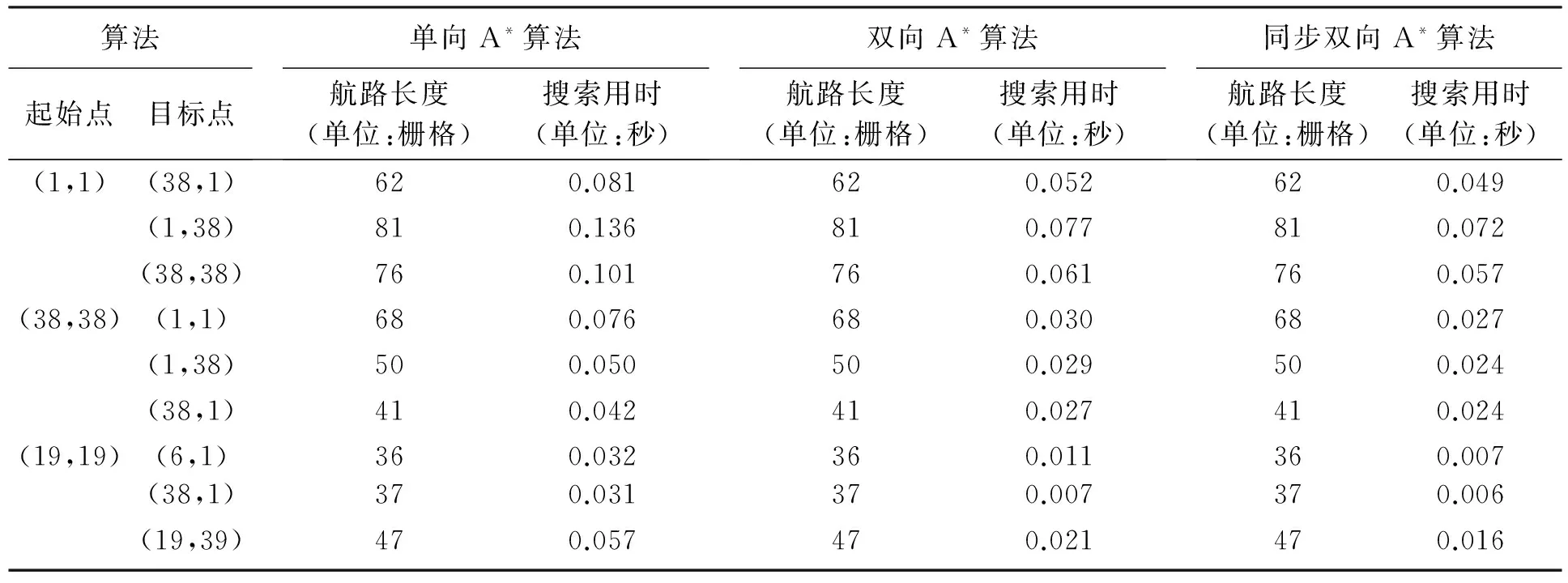
表1　数据统计表

5　总结

本文提出的同步双向A*搜索算法，可以为无人机在城市环境下规划出航路，在保证航路最优且可飞的情况下，较大地提升了航路规划的速度。下一步的研究方向是把该算法应用在三维环境中并测试其性能。

[1]SZCZERBA ROBERT J.Robust algorithm for real-time route planning[J].IEEE Transaction son Aerospace and Electronic Systems(S0018-9251),2000,36(3):869-878.

[2]何雨枫,曾庆化,王云舒,等.室内微型飞行器实时路径规划算法研究[J].电子测量技术,2014,2:23-27.

[3]LAVALLE SM,KUFFNER J J.Rapidly-exploring random trees:progress and prospects[C].Proceedings of the Fourth Workshop on the Algorithmic Foundations of Robotics.Dartmauth，MA,2000:293-308.

[4]黄文刚，张 怡，姜文毅，等.基于改进稀疏A*算法的无人机航路规划[J].遥测遥控,2012,33(6):12-16.

[5]WANG N,GU X,CHEN J,et al.A hybrid neural network method for UAV attack route integrated planning[C].The 6th International Symposium on Neural Networks,Wuhan,2009,5553:226-235.

[6]GENG Q,ZHAO Z.A kind of route planning method for UAV based on improved PSO algorithm[C].The 25th Chinese Control and Decision Conference Guiyang,2013:2328-2331.

[7]陈谋，肖健，姜长生.基于改进蚁群算法的无人机三维航路规划[J].吉林大学学报(工学版),2008,38(4):991-995.

[8]RODRIGUEZ S,TANG X,LIEN J,et al.An obstacle-based rapidly-exploring random tree[C].The 2006 IEEE International Conference on Robotics and Automation,ICRA 2006,2006,Orlando,FL,United states.

[9]宋建梅,李侃.基于A*算法的远程导弹三维航迹规划算法[J].北京理工大学学报,2007,27(7):613-617.

[10]ZHANG B,MAO Z,LIU W,et al.Geometric reinforcement learning for path planning of UAVs[J].Journal of Intelligent and Robotic Systems:Theory and Applications,77(2):391-409.

[11]郝振国,王玉玫.双向A*算法在军事路径规划中的应用[J].计算机工程与应用,2011,47(29):246-248.

[12]BAOCHANG ZHANG,WANQUAN LIU,ZHILI MAO,et al.Cooperative and geometric learning algorithm (CGLA) for path planning of UAVs with limited information[J].Automatica,2014,50(3):809-820.

[13]KUWATA Y,TEO J,KARAMAN S,et al.Motion planning in complex environments using closed-loop prediction[C].The AIAA Guidance,Navigation and Control Conference and Exhibit,Honolulu,HI,United states,2008.

[14]张彪,曹其新,王雯珊.使用三维栅格地图的移动机器人路径规划[J].西安交通大学学报,2013,47(10):57-61.

[15]武雪玲,李清泉,任福.基于分层分块数据组织的双向A*算法[J].测绘信息与工程,2006,31(6):1-3.

[16]董文洪,易波,栗飞.无人机航路规划环境模型研究[J].计算机工程与应用,2012,48(15):236-239.

(责任编辑：刘划英文审校：赵亮)

Urban UAV route planning based on bidirectional A*algorithm

LIN Na,LI Tian-xiao

(College of Computer Science,Shenyang Aerospace University,Shenyang 110136,China)

The bidirectional A*algorithm was applied in the urban UAV route planning.Compared with the traditional A*search algorithm,the synchronous bidirectional A*search algorithm,the improved bidirectional A*search algorithm,has higher search efficiency,and saves great time of route planning.Experiment was built to realize the forward search and the backward search working on the same time by using the grid method to build the environment model for UAVs.It was fully considered that the urban environment to determine the grid size while building the environment model.Experimental result shows that the synchronous bidirectional A*algorithm is more efficient since it can make the route planning faster for UAVs and the route flyable.

unmanned aerial vehicle (UAV);bidirectional A*;grid;the urban environment;route planning

2015-10-28

辽宁省自然科学基金联合基金(项目编号:2015020008);辽宁省自然科学基金(项目编号:20102175);辽宁省高等学校优秀人才支持计划(项目编号：LJQ2012011)。

林娜(1977-)，女，辽宁沈阳人，副教授，主要研究方向：无人机航路规划，智能交通，E-mail：lin_na2000@163.com。

信息科学与工程

2095-1248(2016)04-0055-06

TP391.9

A

10.3969/j.issn.2095-1248.2016.04.010