基于统计能量分析的整流罩能量损耗因子确定

殷　骏，方　勃

(沈阳航空航天大学 航空航天工程学部(院)，沈阳 110136)



基于统计能量分析的整流罩能量损耗因子确定

殷骏，方勃

(沈阳航空航天大学 航空航天工程学部(院)，沈阳 110136)

对整流罩进行宽频激励虚拟实验，测得整流罩的振动响应和声腔的声压响应;对整流罩建立统计能量模型。考虑到整流罩是多子结构系统，子系统间存在间接耦合的现象,根据虚拟实验响应、利用修正的功率入射法算出各子系统的内损耗因子、直接耦合损耗因子和间接耦合损耗因子，得到更贴近实际的结果。

统计能量分析；整流罩；内损耗因子；耦合损耗因子

火箭整流罩在高速飞行时会处于很严峻的高频声振环境中[1],这会加速整流罩的疲劳破坏，同时整流罩内的高声压会破坏整流罩内的精密元件。而传统的确定性方法，如有限元法和边界元法存在理论上的限制，同时计算成本大，在高频段效率很低。统计能量法将能量作为基本参数，能从能量导出位移和速度等响应，可方便而高效地处理高频声振问题[2]。

HarijonoDjojodihardjo将边界元—有限元运用于声振耦合结构，并为轻质量结构的声振耦合分析提出一种方法作为基准[1]。D.J.Chappell基于统计能量法提出动力能量分析，该方法能将阻尼、方向性和弯曲的效果考虑进去，这样整体结构的分析就能更详细清晰[2]。傅学军分析了有限元、边界元和统计能量在结构声振分析中可以应用的频率范围，得出统计能量法的应用频率范围最宽，而且在中高频段响应分析结果的精度很高[3]。

本文对整流罩进行有限元虚拟试验，对整流罩施加宽频点激励，测出测点的速度响应和声腔的声压，接着建立整流罩的统计能量模型。由于整流罩结构复杂，子系统间存在间接耦合现象，而修正的功率射入法适用于非保守耦合和间接耦合的情形，所以本文运用修正的功率入射法计算整流罩的内损耗因子、直接耦合损耗因子和间接耦合损耗因子，相比于传统的直接认定整流罩子系统间的间接耦合损耗因子为零的做法[4]算出的统计能量参数更贴近实际。

1　整流罩有限元虚拟试验

本文研究的整流罩如图1所示，分为头锥、前锥、柱段和倒锥4段箭身，内部为空腔，高度为10m，最大半径为1.65m，厚度为10mm，结构阻尼为0.06，材料为铝。头锥的质量为92.25kg，前锥的质量为396.3kg，柱段的质量为2 128kg，倒锥的质量为147.17kg，整流罩内的空腔体积为78.14m3，内壁表面积为108.47m2。

依次对头锥、前锥、柱段、倒锥加宽频点力激励，大小为1N，频率为1 000～6 000Hz，分析频程为1/3倍频程。在每个独立激励试验中，每个部分(包括声腔)随机选5个测点，测出速度的幅值F和声腔的声压，测出激励点力方向上的速度幅值V和相位差。

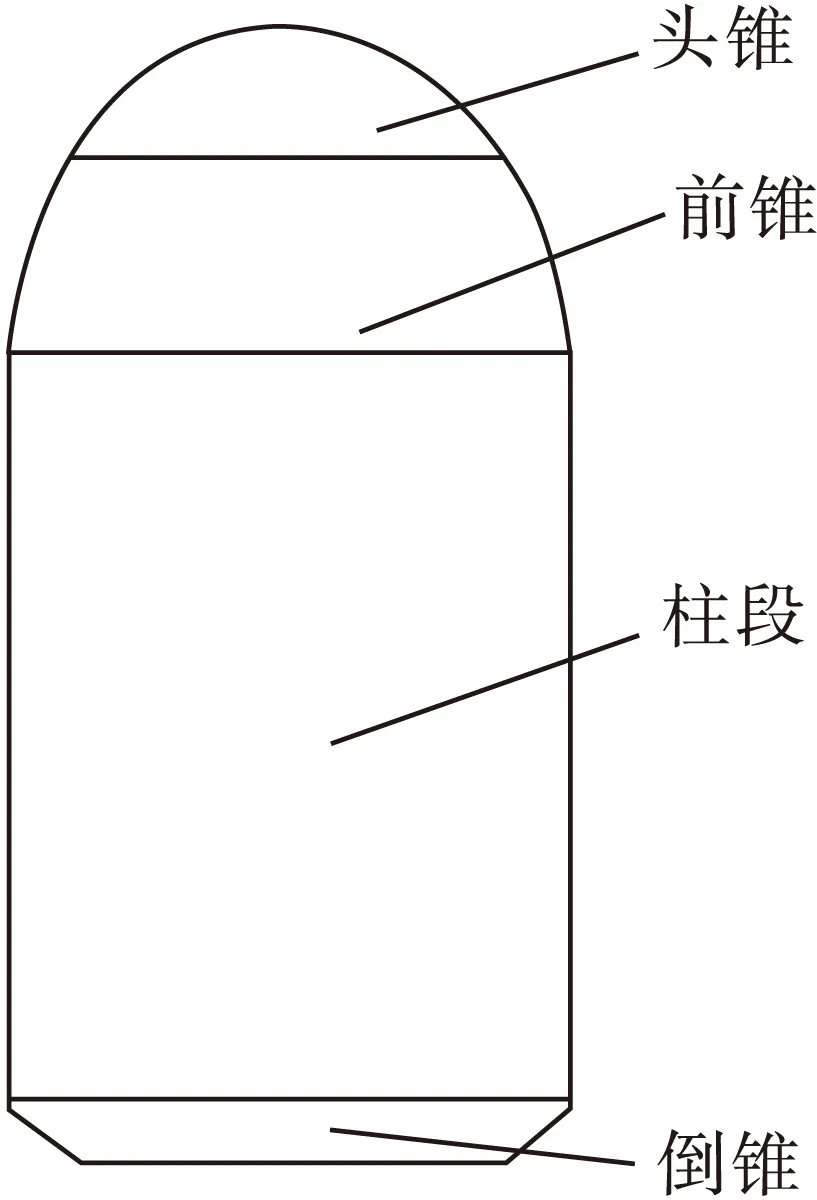
图1　整流罩

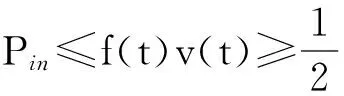
表1　单独激励头锥时的输入功率

表2　单独激励前锥时的输入功率

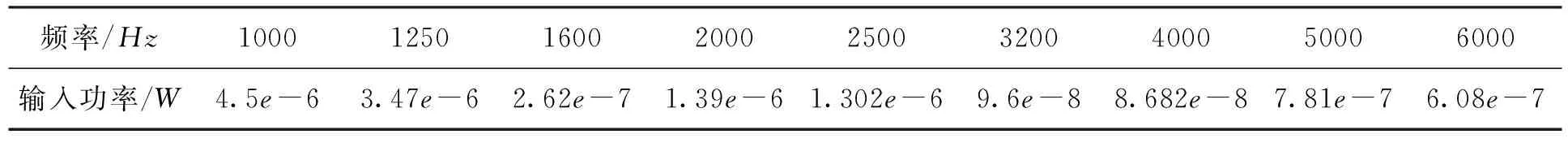
表3　单独激励柱段时的输入功率

表4　单独激励倒锥时的输入功率

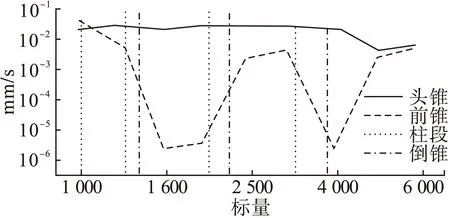
图2　单独激励头锥时的各子系统的速度响应

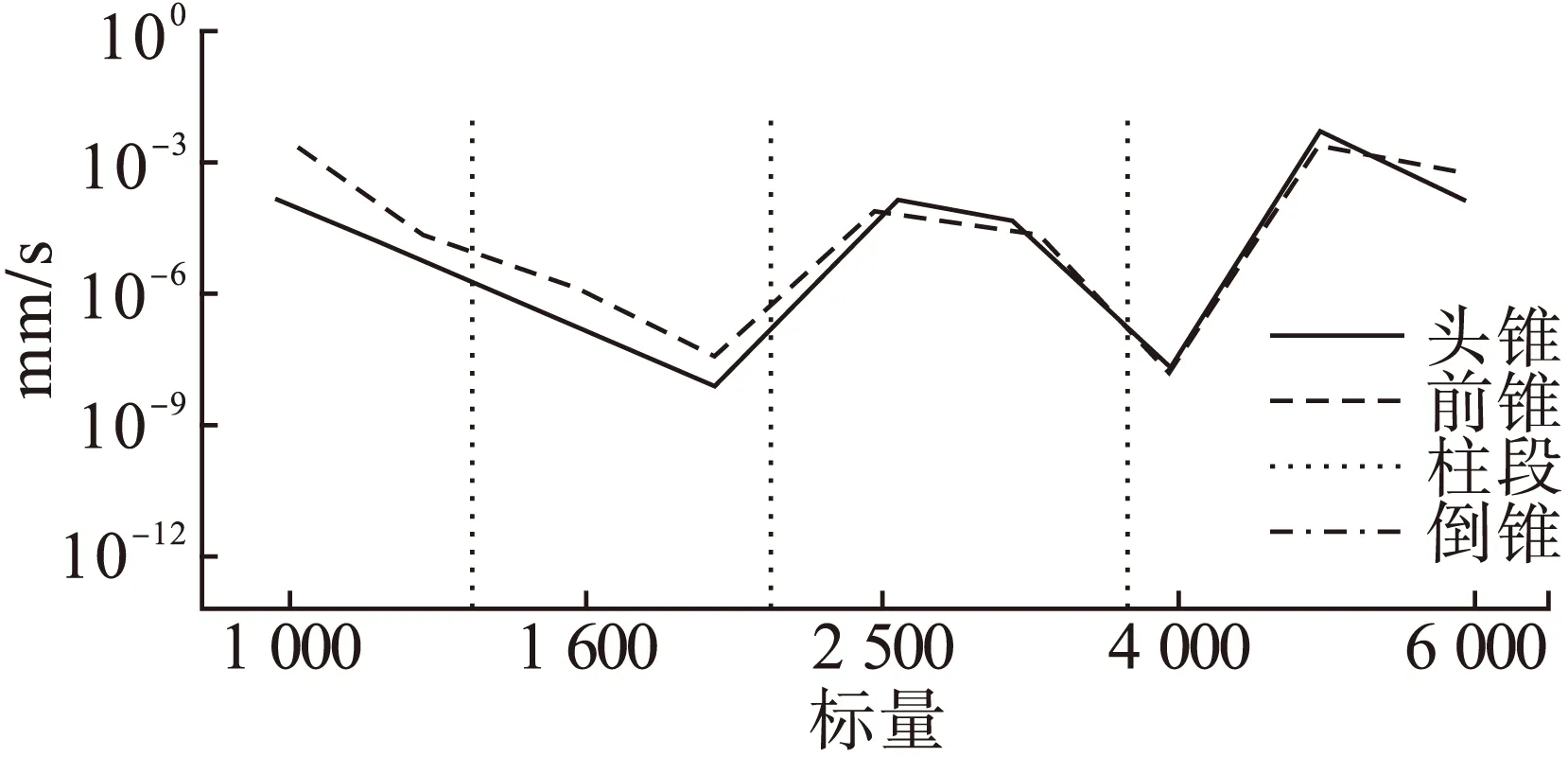
图3　单独激励前锥时的各子系统的速度响应

单独激励柱段时的速度响应如图4所示:

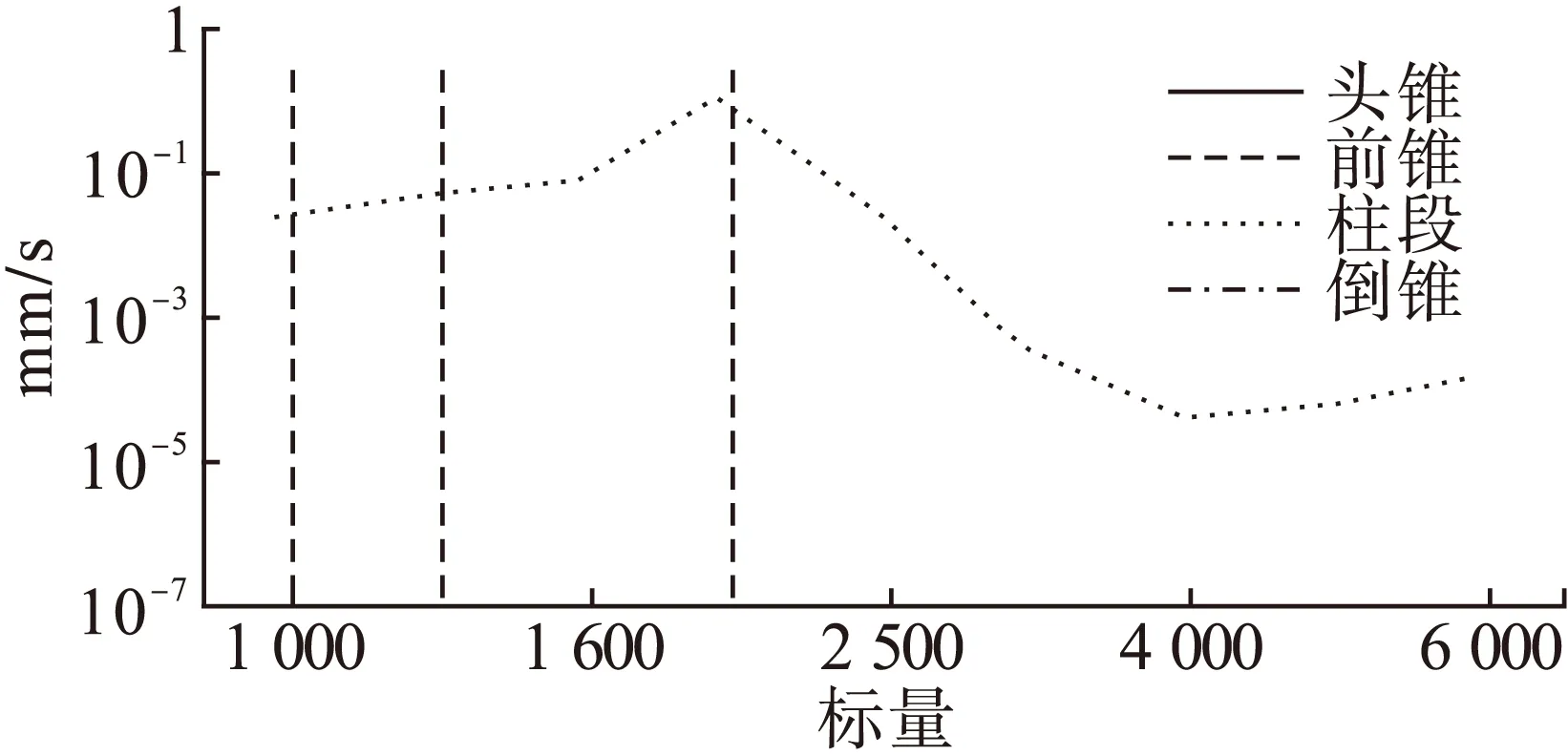
图4　单独激励柱段时的各子系统的速度响应

单独激励倒锥时的速度响应如图5所示:

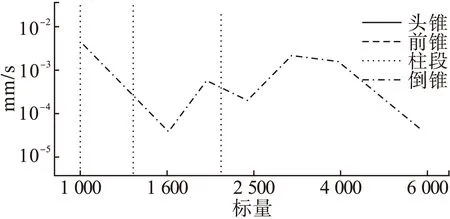
图5　单独激励倒锥时的各子系统的速度响应

2　统计能量分析

2.1统计能量模型确立

本文将整流罩划分为头锥、前锥、柱段、倒锥和声腔5个子系统，如图6所示。

2.2内损耗因子的确定

对于声空间子系统5，内损耗因子为[8]

(1)

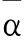
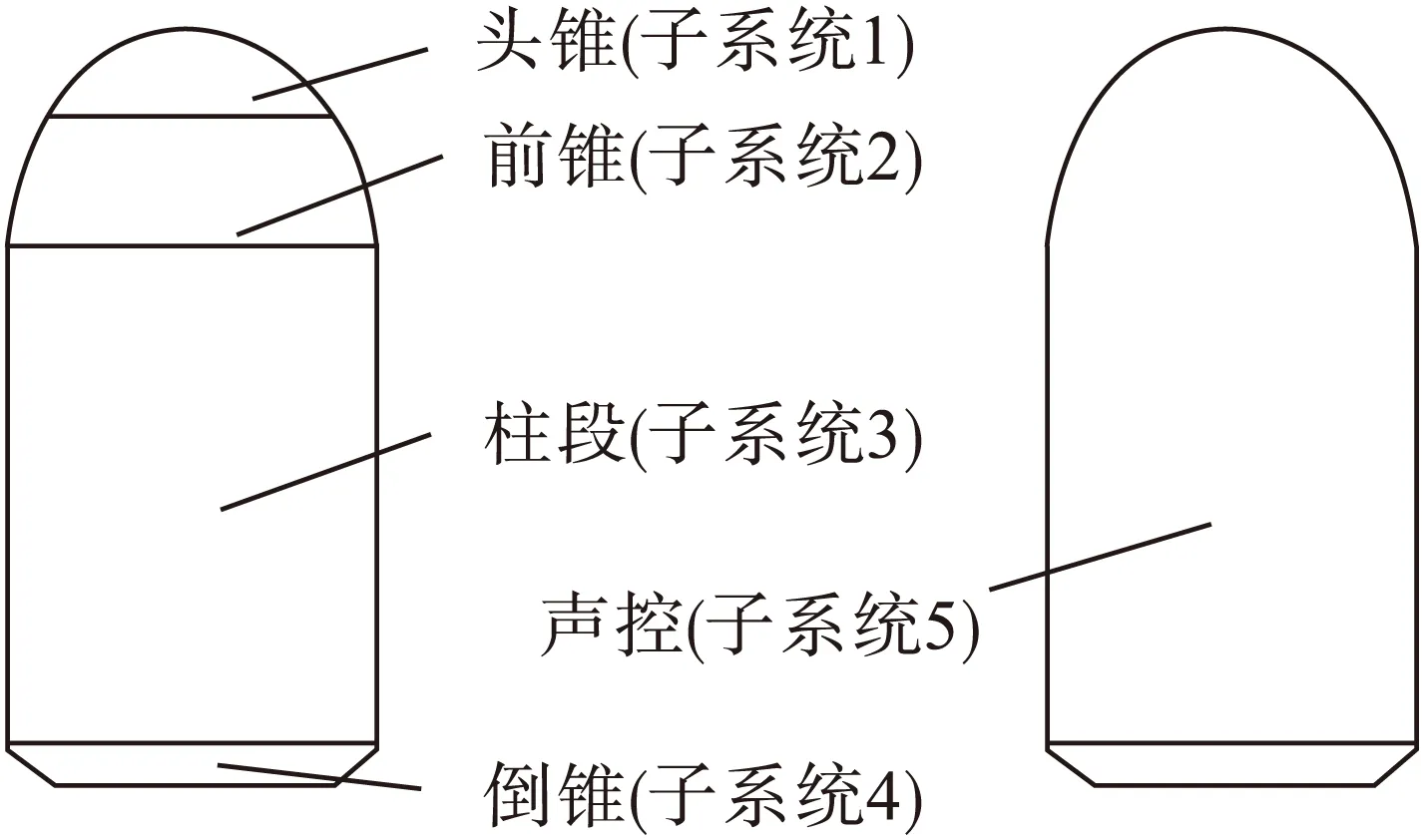
图6　整流罩的统计能量模型

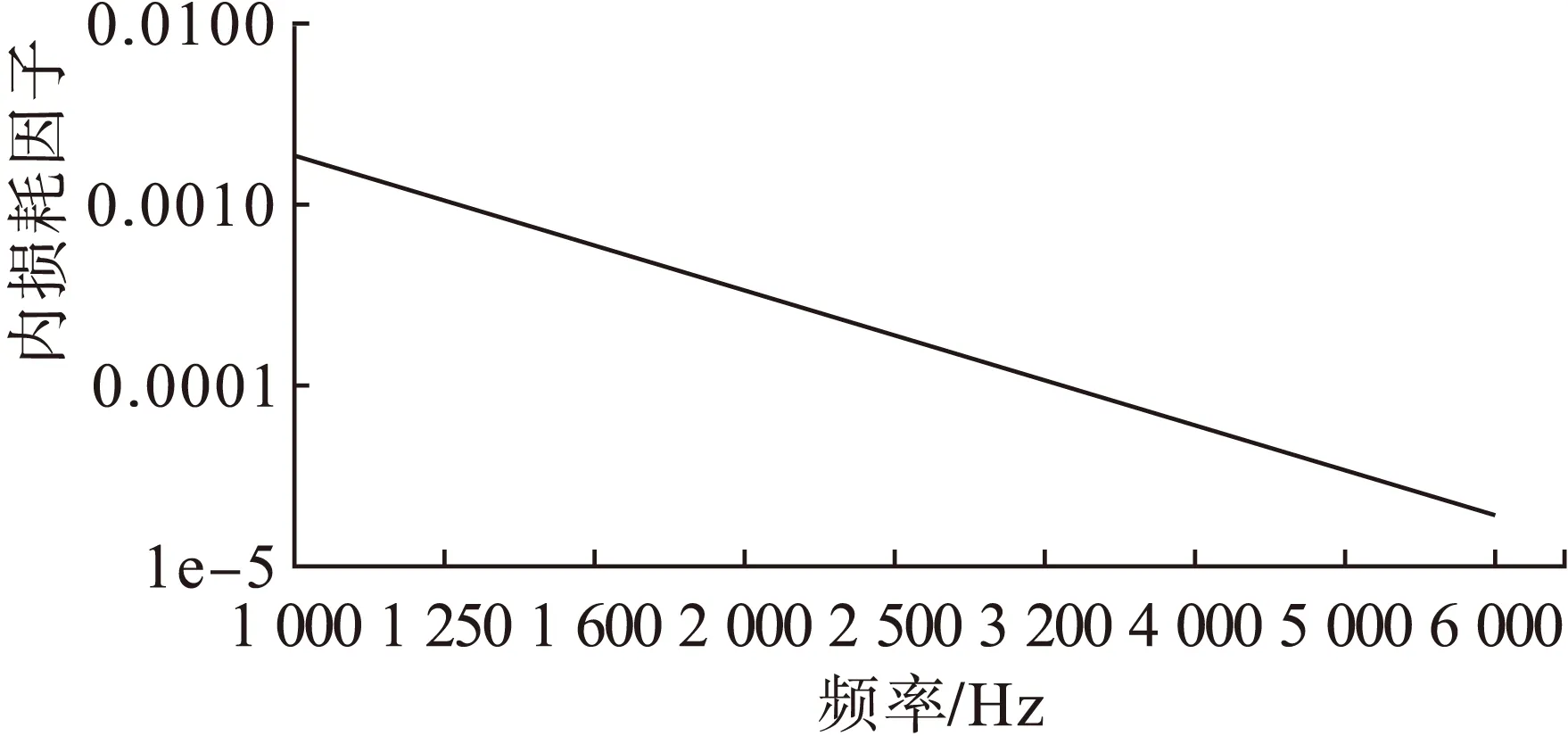
图7　声腔的内损耗因子

依次对头锥、前锥、柱段和倒锥4个子系统加激励时，根据测点的速度算出子系统的能量，再算出子系统间的能量比，将已算出的声空间子系统的内损耗因子和子系统能量比代入方程组(2)中，这样便可算出头锥、前锥、柱段和倒锥的内损耗因子[9-10]。

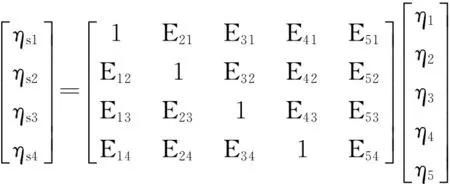
(2)

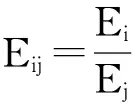
图8　头锥的内损耗因子

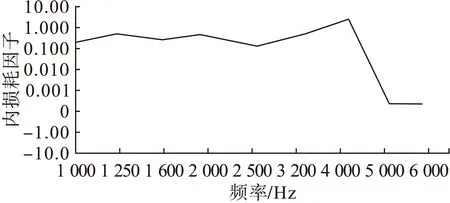
图9　前锥的内损耗因子

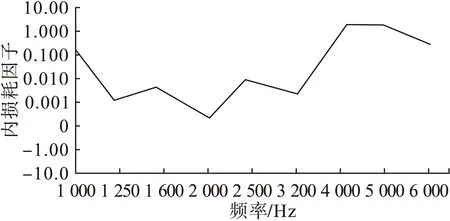
图10　柱段的内损耗因子

图8中，头锥的内损耗因子出现负数，根据相关理论[14]，内损耗因子为负的可能原因为存在强耦合、非保守耦合和频带内的模态数目不符合经典统计能量分析假设。对各个子系统作模态分析，发现头锥在1 250Hz以下时模态数目小于5，不满足统计能量分析的假设，可以推断头锥在低频段的内损耗因子是负的，主要原因是此频段内模态数目少。

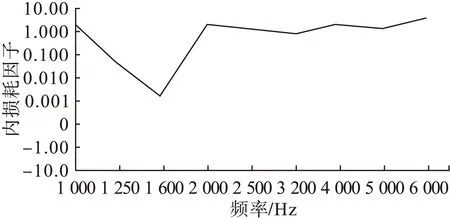
图11　倒锥的内损耗因子

2.3耦合损耗因子的确定

稳态情况下对于本文由5个子系统组成的系统，如果只有子系统i受到外力Fi的激励，则[15]

k=1，…，N和k≠i

上式有4个方程，如果对头锥、前锥、柱段和倒锥依次施加激励，则会得到5*4个方程，两边同除Ei，便可得到下面方程组

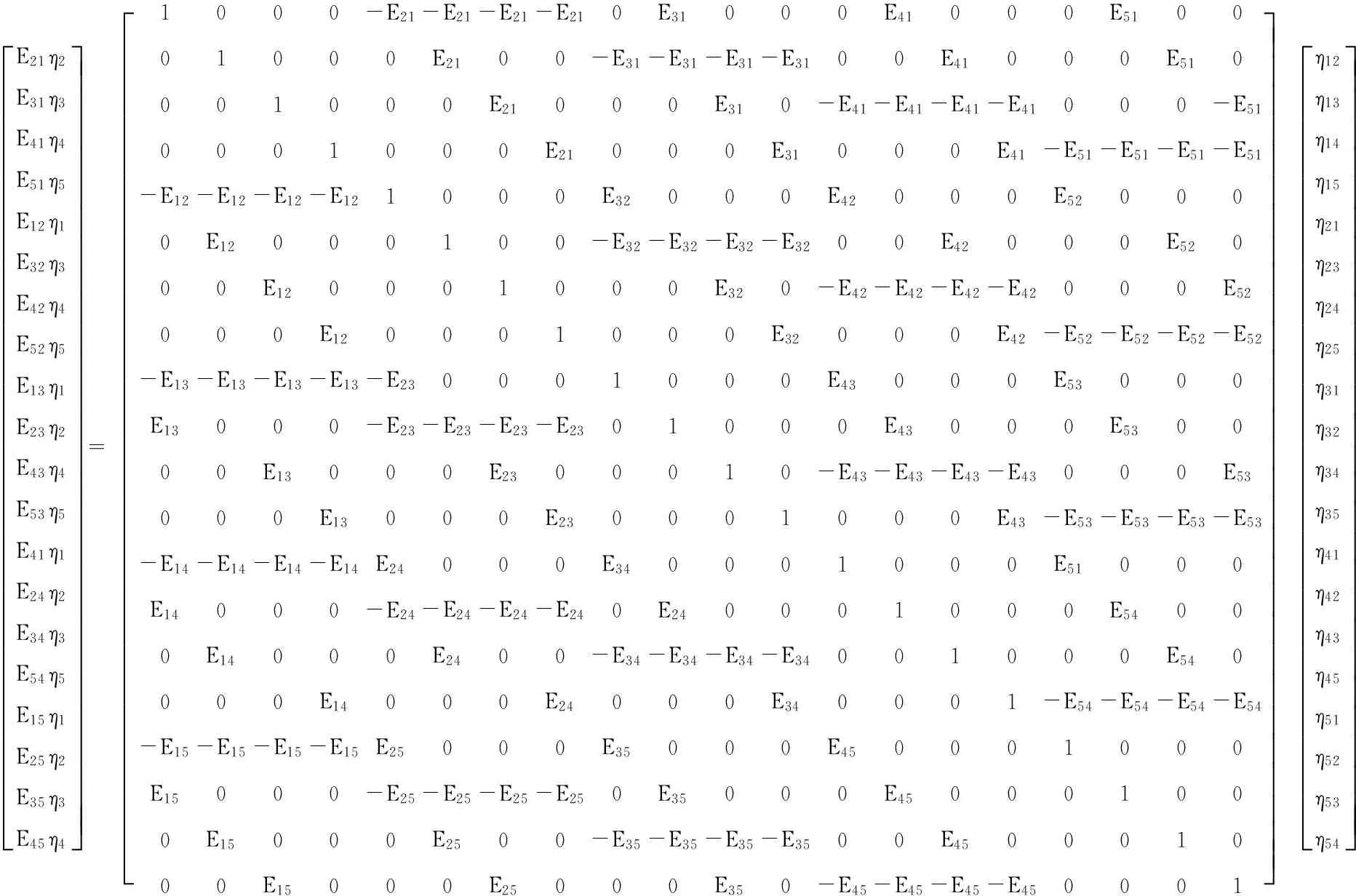
E21η2E31η3E41η4E51η5E12η1E32η3E42η4E52η5E13η1E23η2E43η4E53η5E41η1E24η2E34η3E54η5E15η1E25η2E35η3E45η4éëêêêêêêêêêêêêêêêêêêêêêêêêêêêùûúúúúúúúúúúúúúúúúúúúúúúúúúúú=éëêêêêêêêêêêêêêêêêêêêêêêêêêêêêê1000-E21-E21-E21-E210E31000E41000E510001000E2100-E31-E31-E31-E3100E41000E510001000E21000E310-E41-E41-E41-E41000-E510001000E21000E31000E41-E51-E51-E51-E51-E12-E12-E12-E121000E32000E42000E520000E12000100-E32-E32-E32-E3200E42000E52000E120001000E320-E42-E42-E42-E42000E52000E120001000E32000E42-E52-E52-E52-E52-E13-E13-E13-E13-E230001000E43000E53000E13000-E23-E23-E23-E2301000E43000E530000E13000E2300010-E43-E43-E43-E43000E53000E13000E230001000E43-E53-E53-E53-E53-E14-E14-E14-E14E24000E340001000E51000E14000-E24-E24-E24-E240E240001000E54000E14000E2400-E34-E34-E34-E34001000E540000E14000E24000E340001-E54-E54-E54-E54-E15-E15-E15-E15E25000E35000E450001000E15000-E25-E25-E25-E250E35000E450001000E15000E2500-E35-E35-E35-E3500E450001000E15000E25000E350-E45-E45-E45-E450001ùûúúúúúúúúúúúúúúúúúúúúúúúúúúúúúη12η13η14η15η21η23η24η25η31η32η34η35η41η42η43η45η51η52η53η54éëêêêêêêêêêêêêêêêêêêêêêêêêêêêùûúúúúúúúúúúúúúúúúúúúúúúúúúúú

由上式可算出耦合损耗因子，其中柱段到头锥的耦合损耗因子如图12所示。

从图12可看出，虽然柱段和头锥不直接相连，但它们之间也有能量传输，运用修正的功率输入法可以算出间接耦合损耗因子，相比以往直接认定整流罩子系统间的间接耦合损耗因子为零，这样得到的耦合损耗因子更贴近实际。

图12　柱段到头锥的耦合损耗因子

3　结论

本文对整流罩进行虚拟实验，测得振动响应和声压响应。建立统计能量模型，根据虚拟实验的响应结果，运用修正的功率入射法算出整流罩的内损耗因子和耦合损耗因子，得出以下结论：

(1)当频段内模态数目少，不符合经典统计能量分析假设时，会出现负内损耗因子的情况；

(2)由于整流罩是多子结构系统，子系统间存在强耦合的现象，即不直接相连的结构之间存在功率流的传输，用修正的功率输入法可以很好地测量出间接耦合损耗因子，相比以往直接认定整流罩子系统间的间接耦合损耗因子为零，这样算出的结果更符合实际。

[1]DJOJODIHARDJO H.Vibro-acoustic analysis of the acoustic-structure interaction of flexible structure due to acoustic excitation[J].Acta Astronautica,2014(108):129-145.

[2]CHAPPELL D J,LOHEL D,N.SODERGAARD G,et al.Dynamical energy analysis on mesh grids:a new tool for describing the vibro-acoustic response of complex mechanical structures[J].Wave Motion,2014(51):589-597.

[3]傅学军，雷勇军.有效载荷整流罩降噪性能的数值分析和优化设计研究[J].导弹与航天运载技术,2005(279):12-15.

[4]孙目,王小军,潘忠文,等.统计能量分析在飞行器动力学环境预示中的应用[J].导弹与航天运载技术,2009(3):11-14.

[4]A SEÇGIN，S GÜLER，M KARA.Determinations of in-situ energy loss factors of point-connected composite plates[J].Composites Part B Engineering,2015(87):27-32.

[5]TIAN RAN LIN,ANDY C.C.TAN,CHENG YAN,et al.Vibration of L-shaped plates under a deterministic force or moment excitation:a case of statistical energy analysis application[J].Journal of Sound and Vibration,2011(330):4780-4797.

[7]姚德源，王其政.统计能量分析原理及其应用[M].北京：北京理工大学出版社，1995.

[8]J.LEGAULT,J.WOODHOUSE,R.S.LANGLEY.Statistical energy analysis of inhomogeneous systems with slowly varying properties[J].Journal of Sound and Vibration,2014(333):7216-7232.

[9]孙进才.复杂结构的损耗因子和耦合损耗因子的测量方法[J].声学学报，1995(2):127-134.

[10]B.Y.Mao,S.L.Xie,M.L.Xu,et al.Simulated and experimental studies on identification of impact load with the transient statistical energy analysis method[J].Mechanical Systems and Signal Processing,2014(46):307-324.

[11]COTONIA V,LANGLEY R S,SHORTER P J.A statistical energy analysis subsystem formulation using finite element and periodic structure theory[J].Journal of Sound and Vibration,2008(318):1077-1108.

[12]ZAMRI MOHAMED,XUWANG.A deterministic and statistical energy analysis of tyre cavity resonance noise[J].Mechanical Systems and Signal Processing,2015(70-71):947-957.

[13]S.L.XIE,Y.H.ZHANG,Q.XIE,et al.Identification of high frequency loads using statistical energy analysis method[J].Mechanical Systems and Signal Processing,2013(35):291-306.

[14]孙朝晖,孙进才,王冲,等.负损耗因子的成因分析[J].声学学报,1996(5):798-804.

[15]YONGBIN MA,YAHUI ZHANG,DAVID KENNEDY.A hybrid wave propagation and statistical energy analysis on the mid-frequency vibration of built-up plate systems[J].Journal of Sound and Vibration,2015(35):63-79.

(责任编辑：宋丽萍英文审校：赵欢)

Determinationofenergylossfactorsoffairingbasedonstatisticalenergyanalysis

YINJun，FANGBo

(FacultyofShenyangAerospaceEngineering,ShenyangAerospaceUniversity,Shenyang110136，China)

Thevirtualexperimentofthefairingexcitedbybroadbandforcewasconductedtothevibrationresponseoffairingandthesoundpressureofthecavity.Thenthestatisticalenergyanalysismodelofthefaringwasestablished.Inviewoftheindirectcouplingbetweensubsystemsincludedinthefairing,factorsofthedampingloss,thedirectcouplinglossandtheindirectcouplinglosswerecalculatedbasedontheresponsesofvirtualexperimentusingthemodifiedpowerinjectionmethod.Theresultsshowthat,thestatisticalenergyanalysisparametersobtainedweremoreclosetothereality.

statisticalenergyanalysis;fairing;dampinglossfactor;couplinglossfactor

2015-11-16

殷骏(1990-)，男，江苏常州人，硕士研究生，主要研究方向：非线性动力学与结构振动，E-mail：jujuxiaojie@sina.com；方勃(1964-)，男，辽宁省沈阳市，教授，主要研究方向：非线性动力学与结构振动，E-mail：bfang0825@163.com。

2095-1248(2016)04-0038-05

V240.2

A

10.3969/j.issn.2095-1248.2016.04.007