轴承不对中转子振动特性分析

夏　锟，王克明，王　帅

(沈阳航空航天大学 航空航天工程学部(院)，沈阳 110136)



轴承不对中转子振动特性分析

夏锟，王克明，王帅

(沈阳航空航天大学 航空航天工程学部(院)，沈阳 110136)

对轴承不对中的故障转子系统进行了仿真分析和实验研究，得到了系统的振动特性；对比分析了健康转子与存在不同不对中量的故障转子间振动特性的差异。结果表明：当转速到达1/2倍一阶临界转速时，故障转子会发生2倍频共振；转子转速接近一阶临界转速时，转子的基频响应会很大，但系统的不对中振动特征并不明显。

轴承不对中;转子；振动特性

旋转机械转子不对中故障的常见程度仅次于不平衡。不对中可分为两大类，一类是联轴器不对中，另一类是轴承不对中。联轴器不对中又可分为角度不对中、平行不对中以及混合不对中3种情况。M.Xu等推导了联轴器不对中激振力的表达式，并进行了数值模拟以及实验验证[1-2]。M.Chandra Sekhar Reddy等使用扭矩传感器测试了不同不对中形式、不同实验频率的情况下扭矩的变化情况[3]。Tejas H.Patel等分析了联轴器不对中系统在三种不同不对中情况下的振动特性[4]。P.N.Saavedra分析了不同联轴器刚度对转子动力学特性的影响，随后使用实验设备测得了相关参数，得到了不对中量对频谱的影响[5-6]。K.M.AL-Hussain等使用拉格朗日能量法建立了普适性的动力学模型以及运动微分方程，得到了数值解并对瞬态和稳态情况进行了分析[7]。Y.S.LEE等建立了不对中转子-滚珠轴承动力学模型，同时使用实验的方法验证了模型的正确性并得到相关结论[8]。A.W.Lees建立了三螺栓连接联轴器不对中的线性模型，推导了系统的运动方程的表达式，使用数值方法获得了实例的解，并作出了相关分析[9]。Y.Hori建立了考虑联轴器不对中的两跨转子系统模型,使用了传递矩阵法对轴承不对中转子系统进行了稳定性的分析[10]。在国内，冯国全等研究了双转子系统外转子支承轴承存在不对中故障时的振动响应[11]。韩清凯等计算了轴承不对中的单跨转子和联轴器不对中的双跨转子的振动响应[12]。李全坤等建立了带有中介支承的双转子不对中故障系统动力学模型，分析了双转子系统存在平行、角度不对中故障时，内、外转子的振动特性[13]。安学利等分析了考虑刚性联轴器不对中系统的振动特性，由数值分析的结果得到了相应结论[14]。刘扬等建立了不对中-碰摩耦合故障转子系统力学模型和有限元模型，研究了不同转速对转子系统动力学特性的影响[15]。由上述文献可知，国内外对轴承不对中转子的研究相对较少，因此研究轴承不对中转子的振动特性很有意义。

本文计算了健康单盘转子以及存在不同不对中量下单盘转子的不平衡响应，随后使用实验设备对转子进行了实验研究，最后对健康转子和故障转子的仿真、实验结果进行了对比分析。

1　振动特性仿真

1.1转子模型

为了与实验设备对照，选择了单转子系统进行建模，转子的有限元模型如图1所示。转子总长700 mm，被8个节点均分成7个轴段，其中1轴段的直径为12.5 mm，2～7轴段直径均为18 mm。转子支承分别在第2和第8节点，2节点为深沟球轴承，承受轴向力和径向力；8节点为滚棒轴承，仅仅承受径向力。转盘在第5节点，转盘厚度14 mm，直径166 mm，盘上有12个M4螺纹孔，用来增加平衡配重，以平衡转子或者增加不平衡量,此处的不平衡量为4.76 g·cm。

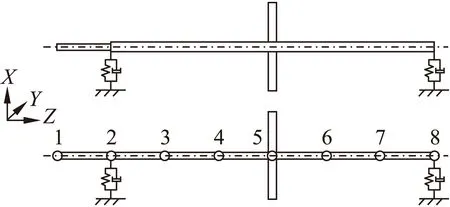
图1　转子模型

使用2节点铁莫申科梁单元对转子进行建模，考虑转子的横向变形和扭转变形，而忽略转子的轴向振动。单元模型如图2所示，而单元广义坐标定义为如下形式

u=[x1，y1，Φy1，Φx1，x2，y2，Φy2，Φx2]

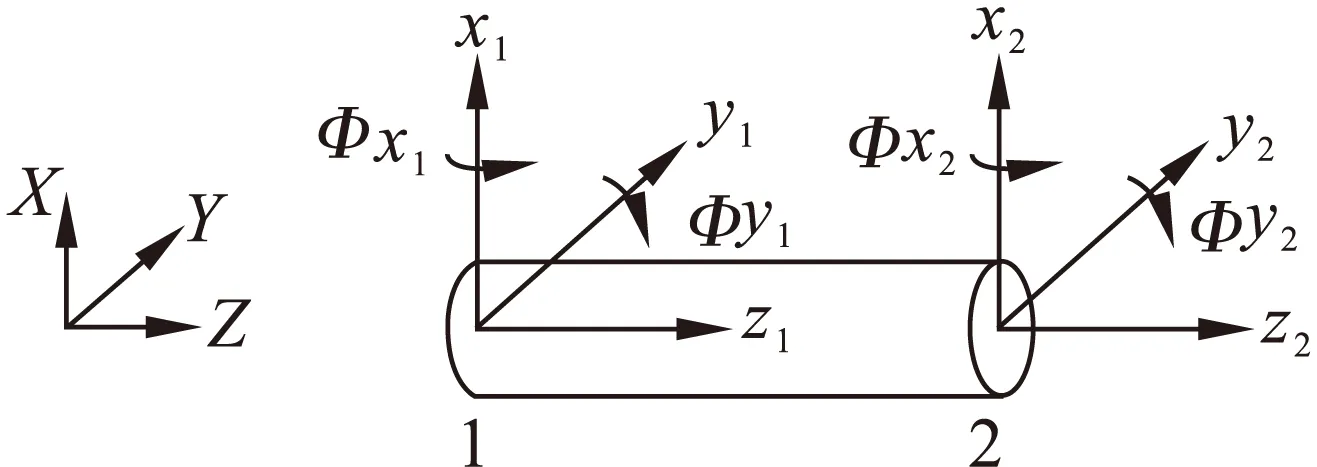
图2　梁单元模型

转子系统的运动方程为

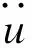
(1)

其中，[M]为整体质量矩阵，[C]为整体阻尼矩阵，[K]为整体刚度矩阵，{Qu}为不平衡激振力，{Qm}为不对中激振力。{Qm}可用加在相对应支承轴承处的弯矩来模拟,由于只有垂直方向上存在不对中量，故不对中激振力的表达式可简化为

该式的推导过程及式中各量的含义见文献[11]。令式(1)中{Qm}+{Qu}={0}，即得式(1)的齐次形式，解该齐次方程可得到系统的临界转速；令{Qm}={0}，即系统不存在不对中，亦即无不对中激振力，只有不平衡激振力，可得到转子的不平衡响应；直接解式(1)，可得到系统在不对中、不平衡激励下的响应。

1.2健康转子仿真结果

计算得到转子的临界转速为2 648.28 r/min。为了便于分析，由临界转速的计算值分别选取1 200 r/min、1 300 r/min、2 400 r/min、3 500 r/min等4个转速对转子进行不平衡响应的仿真，选取7节点为响应点，健康转子在4个转速下的不平衡响应如图3所示。本文中所有图均由轴心轨迹图和响应频谱图组成，响应频谱图右上角的n/nc值表示转速与临界转速的比值。

当转子处于健康状态，转子转速较低时，系统的响应值是相对较小的；当转子转速上升，系统响应随着转速的增大而增大，接近临界转速时，响应值有一个突跃；转速超过一阶临界转速以后，系统响应减小。

图3　健康转子仿真结果

1.3不对中转子仿真结果

在2节点加上垂直方向上的不对中弯矩，以模拟转子不对中的状况，当转子不对中量设定为1 mm时，得到不对中的仿真结果如图4所示。为了与健康转子的仿真结果对照，不对中响应亦使用对数坐标显示。

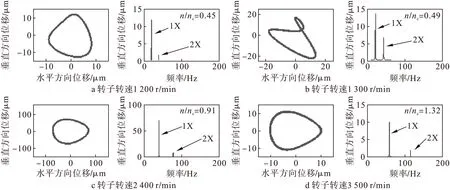
图4　不对中转子仿真结果(不对中量1mm)

当转子不对中量设定为2 mm时，得到的仿真结果如图5所示。

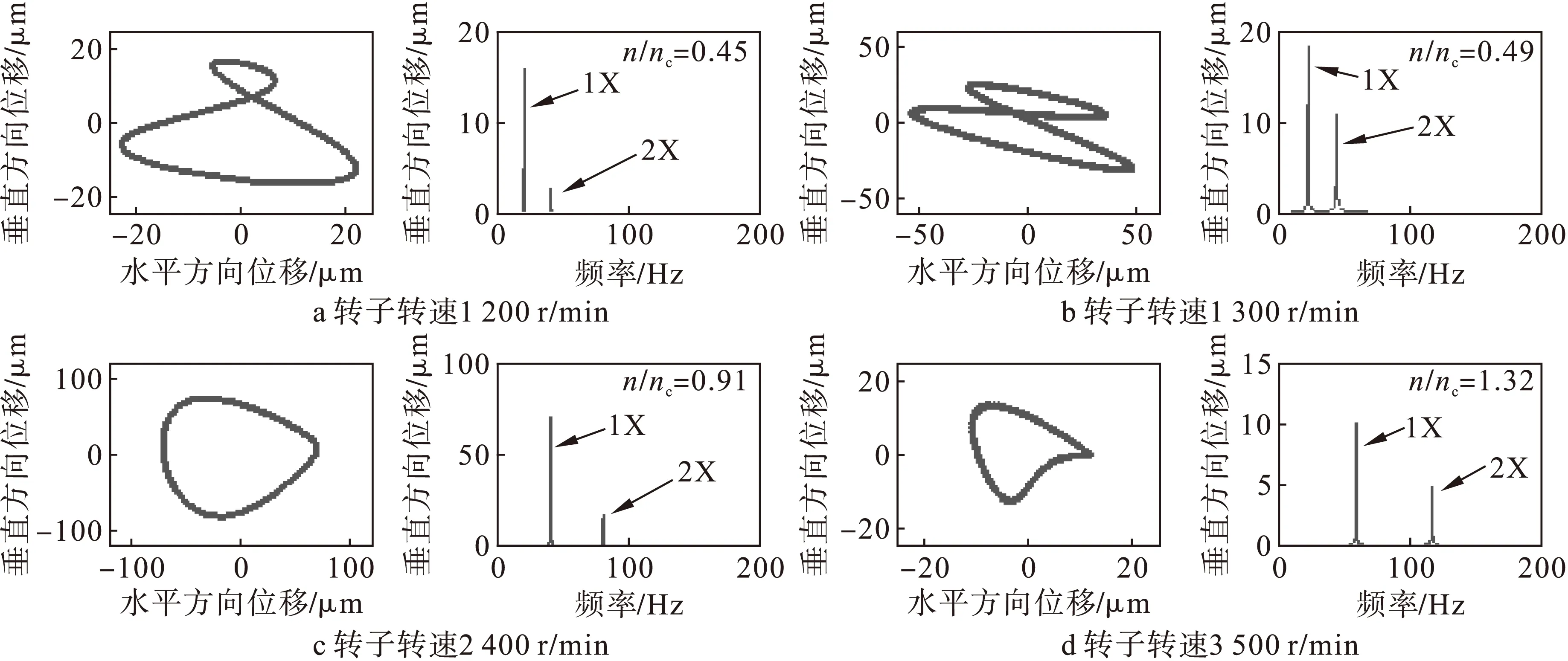
图5　不对中转子仿真结果(不对中量2mm)

当转子存在不对中量(1 mm)时，转子的轴心轨迹发生变化，出现了“8”型的不对中特征；在振动响应图上也出现了2倍频成分，但并不明显。当转速增加到1 300 r/min(n/nc=0.49)时，2倍频的响应增大，这是由于2倍频接近转子的第一阶临界转速，激励的2倍频成分会激起转子的共振[1],而使得不对中响应陡然增大。随着转速的增加，达到第一阶临界转速附近时，转子的基频响应增大，2倍频响应并未增大很多，从而在频谱图上2倍频显得非常小；而此时轴心轨迹几乎仍然保持为一个圆，说明转速接近临界转速时，转子稳定性比低转速时要高。当转子转速达到3 500 r/min(n/nc=1.32)，轴心轨迹出现了变化，不再是一个圆，说明转子的稳定性又开始发生变化，而频谱图上2倍频成分又趋于明显。

当不对中量增加到2 mm时,由轴心轨迹看出，各个转速下的不对中特征相对于不对中量为1 mm时更加明显，特别是转速为3 500 r/min时；而在振动响应频谱图上，2倍频成分也明显多。

2　实验验证

实验环节使用的是本校的转子实验台。在图1所示的7节点处的垂直和水平方向布置电涡流位移传感器。调节电位器，使转速分别稳定在1 200 r/min、1 300 r/min、2 400 r/min、3 500 r/min，采样得到实验数据。

2.1健康转子实验结果

测试得到转子临界转速为2 554 r/min。在圆盘上健康转子增加配重以模拟不平衡量，得到的实验结果如图6所示。由于实验与数值仿真存在一定的误差，因此得到的转子临界转速值与仿真值不同，但实验转速与仿真的工作转速相同，因此n/nc值与数值仿真时的不同。

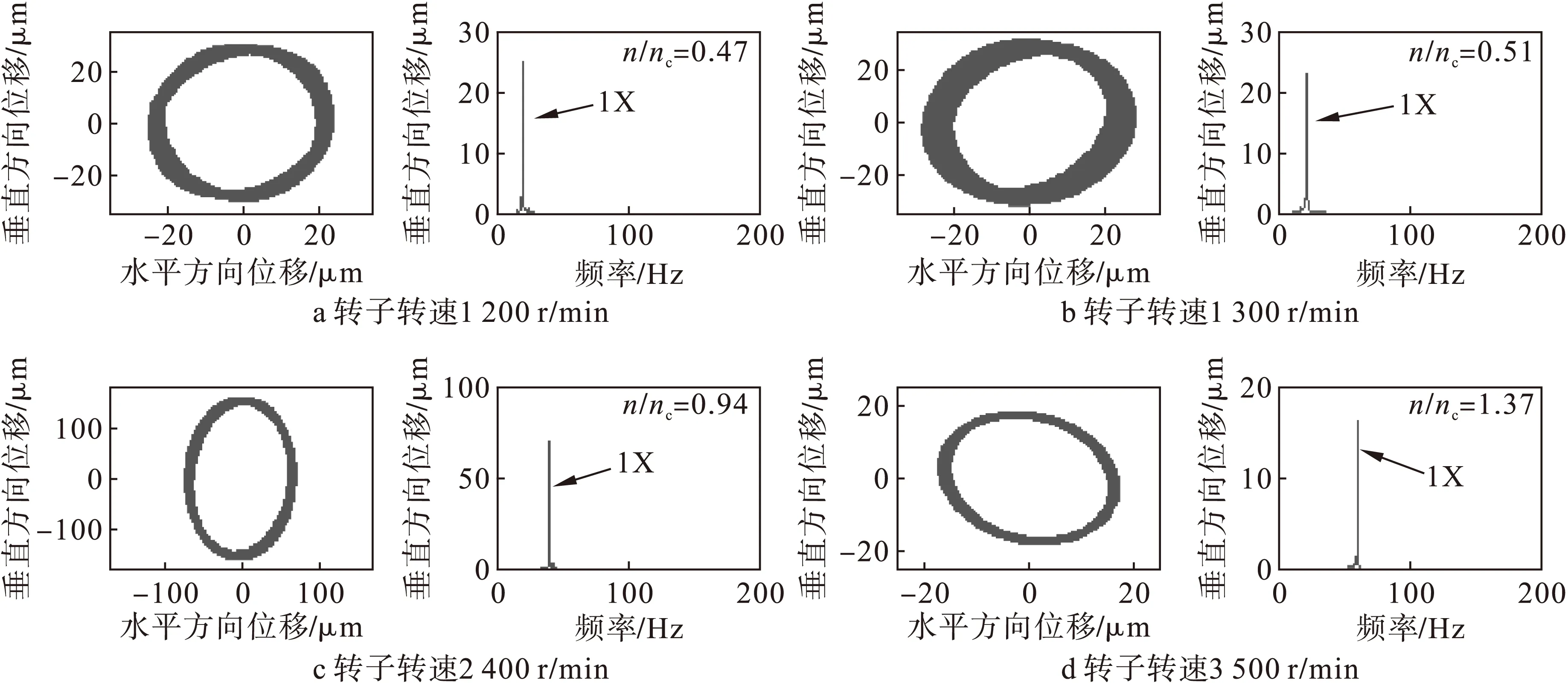
图6　健康转子实验结果

由以上实验结果可以看出，健康转子的不平衡响应的实验结果与仿真结果基本一致。

2.2不对中转子实验结果

在8节点的轴承基座下增加1 mm厚的垫片，用以模拟转子不对中。得到的实验结果如图7所示。

增加轴承基座下垫片的厚度，由1 mm变为2 mm，采集数据后得到的结果如图8所示。

分析图7和图8可知,当故障转子转速处于1/2倍第一阶临界转速时，二倍频的“8”型轨迹非常明显；当转速达到2 400 r/min时(n/nc=0.94)，由于转子的基频响应值远大于二倍频的响应值，二倍频的响应较小,对转子的影响较小,故转子的轴心轨迹也近似于圆。当故障转子转速高于并且远离第一阶临界转速时(n/nc=1.37)，二倍频成分的影响较为明显。而当不对中量加大时，转子各个转速下的响应值变化均较为明显，二倍频成分的幅值显著增大。

2.3误差分析

实验过程中的误差来源主要有以下几个方面：

(1)支承刚度。实验台的支承是由轴承、鼠笼弹性支座以及轴承基座组成。轴承安装在鼠笼弹性支座上，鼠笼弹性支座用螺栓固定在轴承基座上，而轴承基座是用螺栓固定在平台上，可以认为是与平台是一体的，因此鼠笼刚度和轴承刚度的大小决定了支承刚度的大小。鼠笼刚度是经过实验测定的，轴承刚度由计算得到，它们与真实值都存在一定的误差。刚度的大小对临界转速的影响较大，刚度测定带来的误差会使临界转速的值与真实值存在偏差，从而使实验转速与临界转速的距离发生变化，因此响应幅值的大小也会发生变化，从而导致响应值误差出现。由于鼠笼制造存在误差，因此，支承刚度在水平和垂直方向上的大小也可能有差别，因此导致2.1节中转子的轴心轨迹不是一个标准圆。

图7　不对中转子实验结果(不对中量1mm)

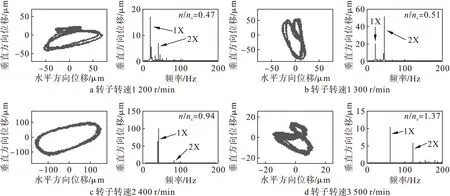
图8　不对中转子实验结果(不对中量2mm)

(2)转子的残余不平衡量。由于转盘的制造误差，转盘上会存在一定的不平衡量，虽然转子在实验前经过单面平衡，但还是会存在一定量的残余不平衡量。该残余不平衡量对不平衡响应的幅值会有影响。

(3)电机转速。由于转速的不稳定或设定转速与实际转速有一定的误差，会导致频谱图上工频成分以及二倍频成分与理想情况会存在微小的偏差。

(4)其他未知噪声。实验过程中会出现许多噪声，这些噪声将会对二倍频成分的识别造成影响。

3　结论

本文针对单转子系统，进行了数值仿真及实验研究，得到以下结论。

(1)对于单盘转子，当轴承不对中量较小时，在较高转速下，不对中故障特征不太明显，但增大轴承不对中量后，不对中故障特征较为明显。

(2)转子存在不对中情况下，当转子转速接近一阶临界转速时，转子基频响应值急剧增大，但二倍频响应并未增大很多，使得二倍频特征不太明显。从轴心轨迹也可以看出，“8”型的特征消失，而变为近似椭圆的形状。

(3)当转子存在轴承不对中故障时，在系统的1/2倍临界转速处会出现2倍频共振，其表现是2倍频响应的突升。

(4)从实验中可以看出，转子存在不对中故障时，不仅仅有2倍频成分出现，还有多倍频成分，但响应值较2倍频成分小很多。

(5)在识别不对中故障时，不能仅仅由振动响应图中是否出现2倍频来判断，必须结合转子的临界转速、工作转速等信息综合考虑。

[1]M.XU.Vibration analysis of a motor-flexible coupling-rotor system subject to misalignment and unbalance,part I:theoretical model and analysis[J].Journal of Sound and Vibration，1994,176(5):663-679.

[2]M.XU.Vibration analysis of a motor-flexible coupling-rotor system subject to misalignment and unbalance,part II:experimental validation[J].Journal of Sound and Vibration,1994,176(5):681-691.

[3]M.CHANDRA SEKHAR REDDY,A.S.SEKHAR.Detection and monitoring of coupling misalignment in rotors using torque measurements[J].Measurement,2015(61):111-122.

[4]TEJASH.PATEL,ASHISHK DARPE.Vibration response of misaligned rotors[J].Journal of Sound and Vibration,2009(325):609-628.

[5]P N SAAVEDRA,D E RAMIREZ.Vibration analysis of rotors for the identification of shaft misalignment Part 1:theoretical analysis[J].Proceedings of the Institution of Mechanical Engineers,2004,218(9):971-985.

[6]P.N.SAAVEDRA,D E RAMIREZ.Vibration analysis of rotors for the identification of shaft misalignment,Part 2:experimental validation[J].Proceedings of the Institution of Mechanical Engineers,2004,218(9):987-999.

[7]K.M.AL-HUSSAIN I.REDMOND.Dynamic response of two rotors connected by rigid mechanical coupling with parallel misalignment[J].Journal of Sound and Vibration,2002,249(3):483-498.

[8]Y.S.LEE,C.W.LEE.Modeling and vibration analysis of misaligned rotor-ball bearing systems[J].Journal of Sound and Vibration,1999,224(1):17-32.

[9]A.W.LEES.Misalignment in rigidly coupled rotors[J].Journal of Sound and Vibration,2007(305):261-271.

[10]Y.HORI,R.UEMATSU.Influence of misalignment of support journal bearings on stability of a multi-rotor system[J].Tribology International,1980,13(5):249-252.

[11]冯国全,周柏卓.内外双转子系统支撑轴承不对中分析[J].振动与冲击，2012,31(7):142-147.

[12]韩清凯,董霄,孙伟,等.两类不对中转子系统的有限元建模与振动分析[C].全国转子动力学学术讨论会,贵阳:2010.

[13]李全坤，廖明夫，蒋云帆.双转子不对中故障振动特性分析[J].机械科学与技术,2014,33(12):1916-1920.

[14]安学利，周建中，向秀桥，等.刚性联接平行不对中转子系统振动特性[J].中国电机工程学报，2008，28(11)：77-81.

[15]刘杨，太兴宇，赵倩，等.转子系统不对中-碰摩耦合故障的动力学特性[J].东北大学学报(自然科学版)，2013,34(4):564-568.

(责任编辑：宋丽萍英文审校：赵欢)

Vibration analysis of rotor system with bearing misalignment

XIA Kun,WANG Ke-ming,WANG Shuai

(Facuty of Aerospace Engineering,Shenyang Aerospace University Shenyang 110136,China)

The vibration characteristics of the faulty rotor system with bearing misalignment were obtained based on the simulation analysis and experimental research.The vibration characteristics between healthy rotor and faulty rotor with different misalignment values were compared and analyzed.The results show that the second harmonic resonance will happen when the rotor speed is close to half of the 1stcritical speed,whereas the first harmonic response is high and the vibration characteristics of the system with misalignment is not obvious when the rotor speed is close to the 1stcritical speed.

misalignment;rotor;vibration characteristic

2015-09-22

夏锟(1987-),男，湖北黄冈人，硕士研究生，主要研究方向：航空发动机强度、振动及噪声，E-mail：379582523@qq.com；王克明(1954-)，男，辽宁沈阳人，教授，主要研究方向：航空发动机强度、振动及噪声，E-mail:wmk308@126.com。

2095-1248(2016)04-0013-06

V231.92

A

10.3969/j.issn.2095-1248.2016.04.003