On Non-commuting Sets in a Finite p-group with Derived Subgroup of Prime Order

Wang Yu-leiand Liu He-guo

(1.Department of Mathematics，Henan University of Technology，Zhengzhou，450001) (2.Department of Mathematics，Hubei University，Wuhan，430062)

Communicated by Du Xian-kun



On Non-commuting Sets in a Finite p-group with Derived Subgroup of Prime Order

Wang Yu-lei1and Liu He-guo2

(1.Department of Mathematics，Henan University of Technology，Zhengzhou，450001) (2.Department of Mathematics，Hubei University，Wuhan，430062)

Communicated by Du Xian-kun

Let G be a finite group.A nonempty subset X of G is said to be noncommuting if xy/=yx for any x，y∈X with x/=y.If|X|≥|Y|for any other non-commuting set Y in G，then X is said to be a maximal non-commuting set.In this paper，we determine upper and lower bounds on the cardinality of a maximal non-commuting set in a finite p-group with derived subgroup of prime order.

finite p-group，non-commuting set，cardinality

2010 MR subject classification:20F18

Document code:A

Article ID:1674-5647(2016)03-0193-05

In this paper，p is always a prime.The notation used is standard，see[1].

Let G be a finite group.A nonempty subset X of G is said to be non-commuting iffor any x，y∈X withAnd further，if|X|≥|Y|for any other noncommuting set Y in G，then X is said to be a maximal non-commuting set in G.We denote by nc(G)the cardinality of a maximal non-commuting set in G，and denote by cc(G)the minimal number of abelian subgroups covering G.Then we can obtain

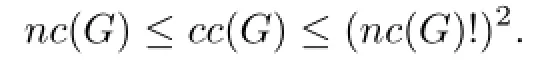
Further，Pyber[2]has shown that there exists some constant c such that

Mason[3]has shown that any finite group G can be covered by at most[|G|/2]+1 abelian subgroups，thus

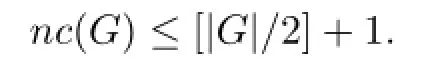
For an extraspecial p-group G with order p2n+1，in the case of p=2，Isaacs has obtained that nc(G)=2n+1(see[4]).In the case of p being odd，Chin[5]has determined thefollowing bounds for nc(G)，

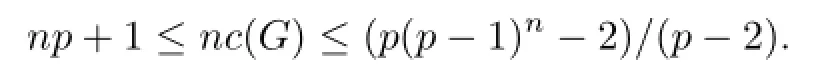
Now we determine upper and lower bounds for the cardinality of a maximal noncommuting sets in a finite p-groups with derived subgroup of prime order.

Lemma 1[6]Let G be a finite p-group with derived subgroup of order p.Then there exist the generators x1，···，x2n，y1，···，ymof G and a generator z of the derived subgroup of G，which satisfy

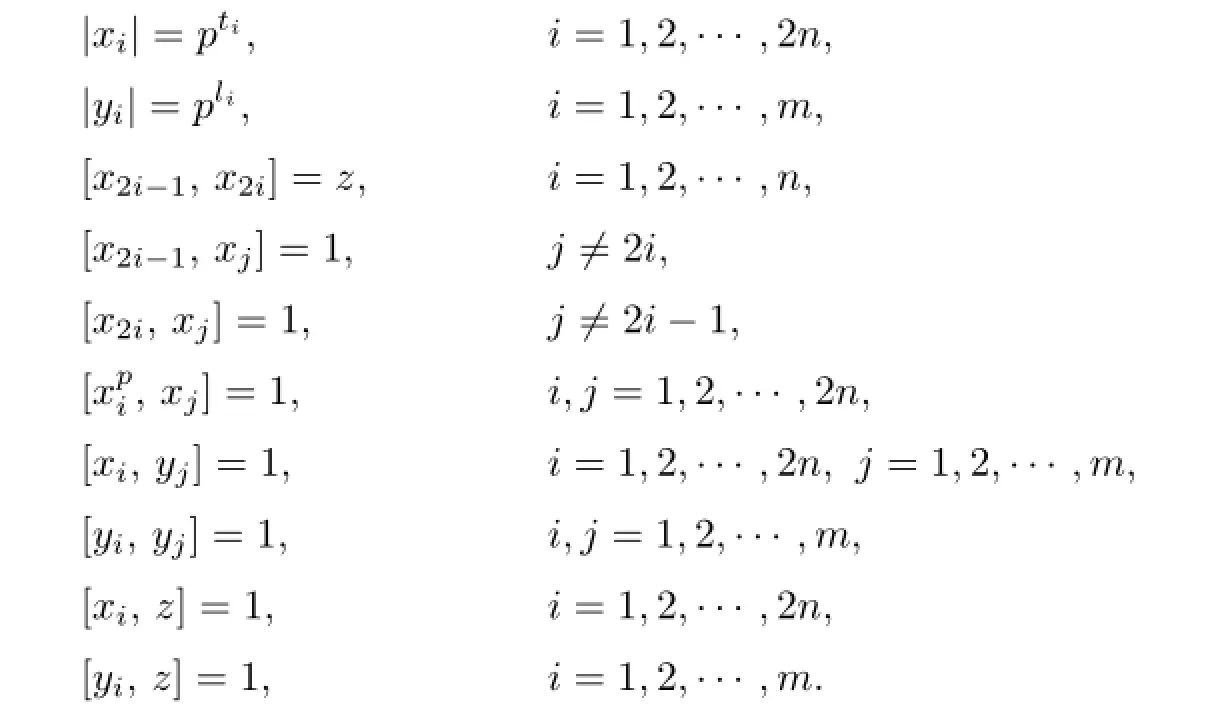
Theorem 1Let G be a finite p-group with derived subgroup of order p，andThen

(1)if p=2，then nc(G)=2n+1；

(2)if p is odd，then np+1≤nc(G)≤(p(p-1)n-2)/(p-2).

Proof.There exist the generators of G:x1，···，x2n，y1，···，ym，z，which satisfy the conditions in Lemma 1.Obviously，

Firstly，we assert

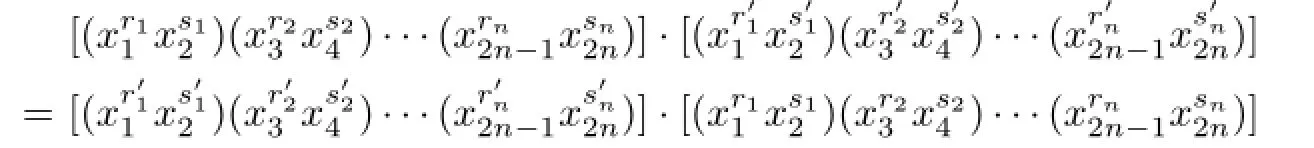
if and only if

In fact，since

and

we have

if and only if

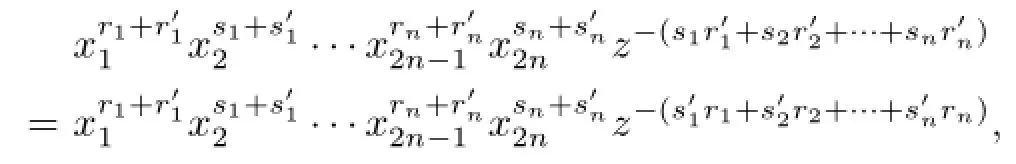
if and only if

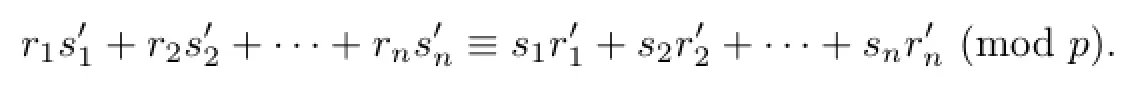
The assertion is true.

Assuming that n=1，we have

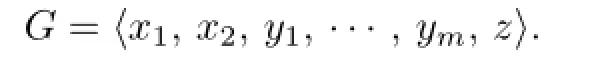
Then G is the union of four sets as

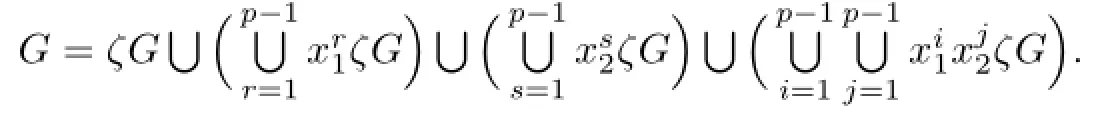
Let R be a non-commuting set of G.Since

we only pick at most one element fromfor R and also at most one element fromfor R.

For any i∈{1，2，···，p-1}，by the assertion above，we have

Then

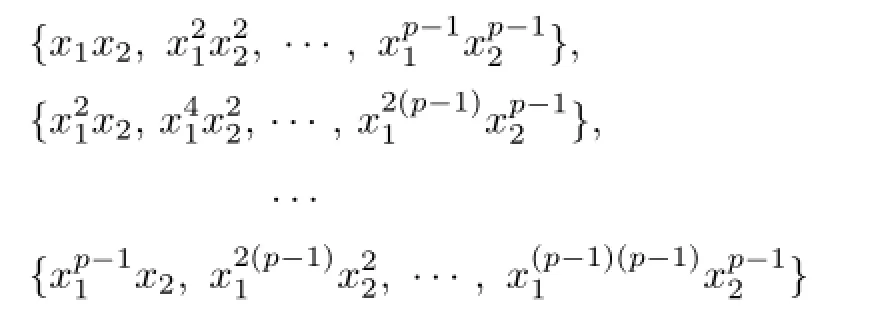
are p-1 mutually disjoint commuting sets.So we only pick at most p-1 elements fromfor R.Hence，the largest possible cardinality of R is

And we take

for R to achieve this cardinality.Therefore，

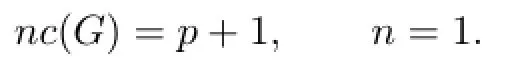
Suppose that n≥2 in the following section and dn=nc(G).Let S be a non-commuting set of G and{x1，x2}⊆S.Note that CG(x1)̸=CG(x2).Let H:=CG(x1)∩CG(x2).Then

Obviously，the derived subgroup of H has order p.

Let dn−1=nc(H).Since

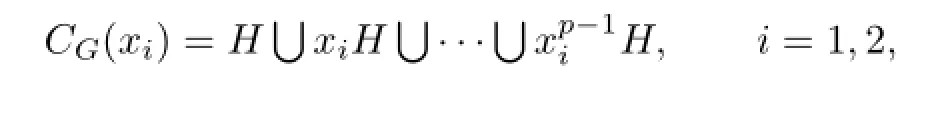
and

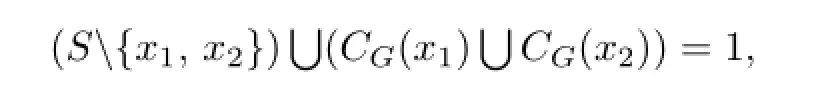
we have

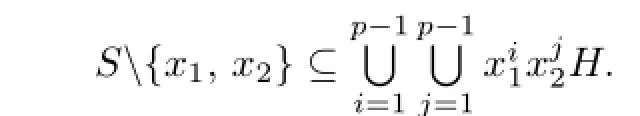
Suppose that S′={h1，h2，···，hdn−1}is a maximal non-commuting set of H.

If p=2，then S{x1，x2}⊆x1x2H.Hence

is a maximal non-commuting set of G，thereby dn=2+dn−1.By this recursion formula and d1=3，we have dn=2n+1.

Suppose that p＞2.It is easy to know that

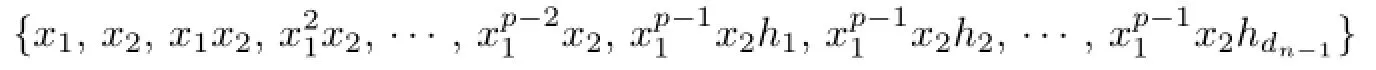
is a non-commuting set of G，but this set cannot be a maximal non-commuting set of G. Hence dn≥dn−1+p.By this recursion formula and d1=p+1，we have

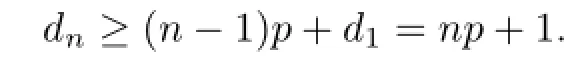
Considering the following(p-1)2sets:

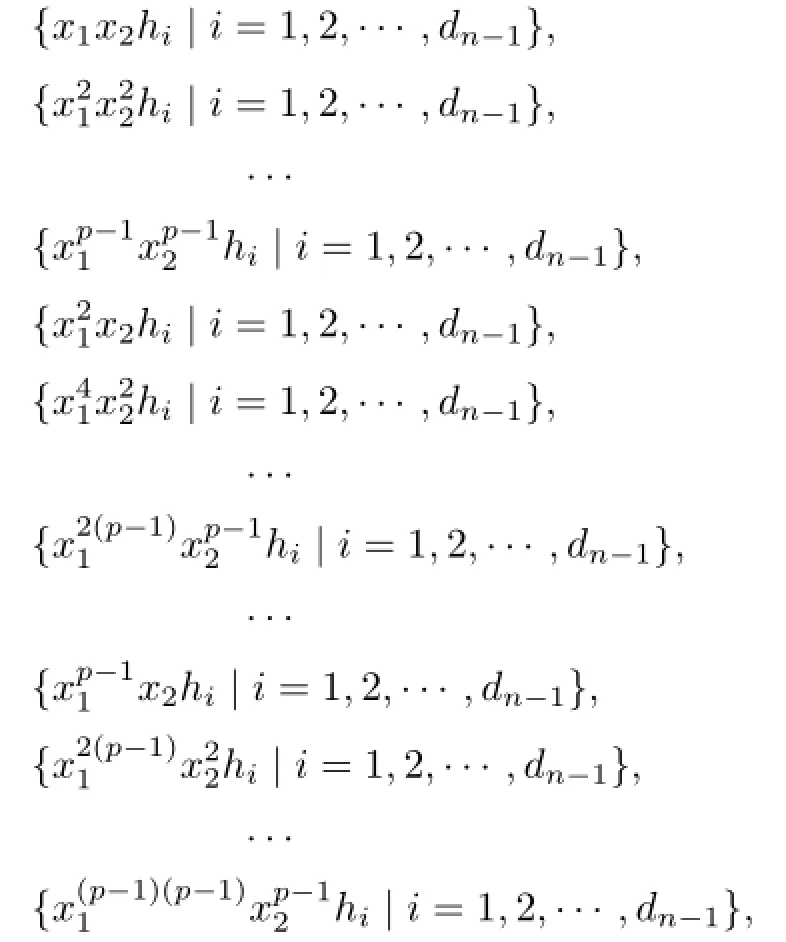
we pick one element from each set above and obtain(p-1)2elements，and these elements are just left coset representatives of left cosetsHence we may pick elements from(p-1)2sets above for S{x1，x2}for convenience.Since the following sets are all commuting sets，

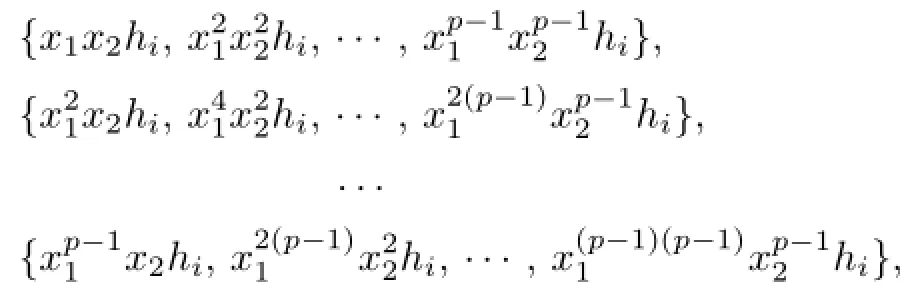
where i=1，2，···，dn−1，we pick elements from the following sets for S{x1，x2}，

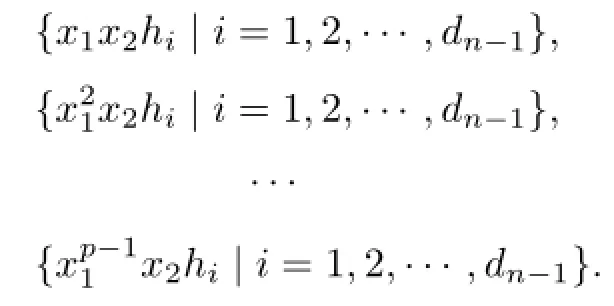
It follows dn≤2+(p-1)dn−1.By the recursion formula and d1=p+1，we have

Hence，when n≥2，

Obviously，this result generalizes the main theorem in[5].

References

[1]Robinson D J S.A Course in the Theory of Groups(Second edition).New York:Springer-Verlag，1996.

[2]Pyber L.The number of pairwise non-commuting elements and the index of the center in a finite group.J.London Math.Soc.(2)，1987，35(2):287–295.

[3]Mason D R.On coverings of a finite group by abelian subgroups.Math.Proc.Cambridge Philos. Soc.，1978，83(2):205–209.

[4]Bertram E A.Some applications of graph theory to finite groups.Discrete Math.，1983，44: 31–43.

[5]Chin A Y M.On non-commuting sets in an extraspecial p-group.J.Group Theory，2005，8: 189–194.

[6]Blackburn S R.Groups of prime power order with derived subgroup of prime order.J.Algebra，1999，219:625–657.

10.13447/j.1674-5647.2016.03.01

date:Feb.9，2015.

The NSF(11301150，11371124)of China，the NSF(142300410134)of Henan Province and Plan for Scientific Innovation Talent(11CXRC19)of Henan University of Technology.

E-mail address:yulwang@163.com(Wang Y L).