Extended tanh-function Method for Solving Traveling Wave Solutions of Nonlinear Kundu Equation

Cai Hua，Guo Ning，Chang Jing，Liu Li-huanand Wu Xian-na

(1.School of Mathematics，Jilin University，Changchun，130012)

(2.General Office，CPECC Jilin Design Branch，Jilin City，Jilin，132022)

(3.College of Information Technology，Jilin Agricultural University，Changchun，130118)

(4.Fundamental Department，Aviation University of Air Force，Changchun，130022)

(5.Group of Mathematics，No.1 Middle School of Heze，Heze，Shandong，274000)

Communicated by Li Yong



Extended tanh-function Method for Solving Traveling Wave Solutions of Nonlinear Kundu Equation

Cai Hua1，Guo Ning2，Chang Jing3，Liu Li-huan4and Wu Xian-na5

(1.School of Mathematics，Jilin University，Changchun，130012)

(2.General Office，CPECC Jilin Design Branch，Jilin City，Jilin，132022)

(3.College of Information Technology，Jilin Agricultural University，Changchun，130118)

(4.Fundamental Department，Aviation University of Air Force，Changchun，130022)

(5.Group of Mathematics，No.1 Middle School of Heze，Heze，Shandong，274000)

Communicated by Li Yong

In this paper，by using the balancing method and the extended tanhfunction method，we obtain the exact traveling wave solutions of Kundu equation with fifth-order nonlinear term.Applications of this method to some other nonlinear partial differential equations are also presented.

extended tanh-function method，Kundu equation，traveling wave solution

2010 MR subject classification:35C07，35C99

Document code:A

Article ID:1674-5647(2016)03-0281-08

1　Introduction

It is well known that complex physical phenomena are described by nonlinear partial differential equations.The solutions of these equations have important significance in mathematical physics and engineering.Therefore，investigating traveling wave solutions is becoming significant.In the past several decades，various methods have been proposed such as the inverse scattering method(see[1])，Darboux transformation(see[2])，the homogeneous balance method(see[3])，Jacobi elliptic function expansion method(see[4])，the(G′/G)-expansionmethod(see[5]–[6])，the tanh-function method(see[7])and the extended tanh-function method(see[8]).

Consider the Kundu equation with fifth-order nonlinear term

where c3，c5，s2and r are real numbers.For convenience we rewrite the equation(1.1)as follows

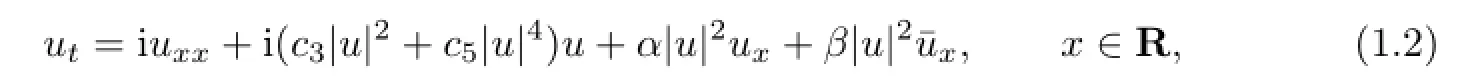
where α=2s2+r and β=s2+r.It is easy to see that the equations(1.1)and(1.2)contain some special cases as follows:

(i)When c3=c5=s2=0，the equation(1.1)becomes the nonlinear Schr¨odinger equation，i.e.，

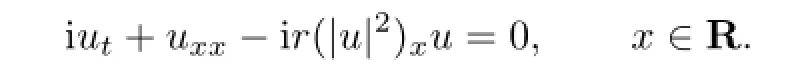
(ii)When c3=c5=0，the equation(1.1)becomes the nonlinear Schr¨odinger equation with fifth-order term，i.e.，

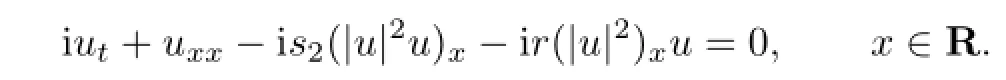
(iii)When c3=c5=0，s2=-δ and r=-s2，the equation(1.2)becomes the Chen-Lee-Liu equation，i.e.，

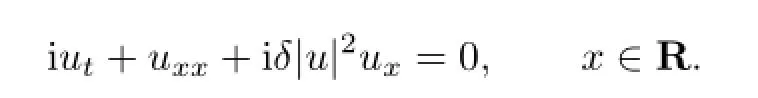
(iv)When c5=2δ2，s2=2δ and r=-2s2，the equation(1.2)becomes a Gerdjikov-Ivanov equation，i.e.，

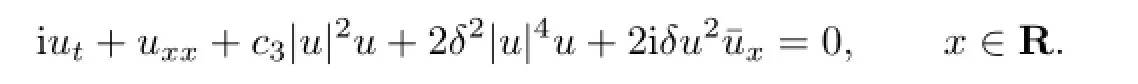
Hence it is significant to study the exact solutions of the Kundu equation.The exact traveling wave solutions of it have been investigated by some authors.Biawas[9]studied the generalized Kundu equation and obtained a solitary solution of it by integration.In [10]，the authors obtained the exact solitary waves of Kundu equation by using proper transformations and coefficient method.In[11]，the author obtained a new exact solitary wave solution of Kundu equation based on auxiliary equation method and the method of an auxiliary equation of triangle function type with function transformation.The aim of this paper is to explore new exact traveling wave solutions for(1.1)by the extended tanh-function method.

2　Extended tanh-function Method

Consider a nonlinear evolution equation

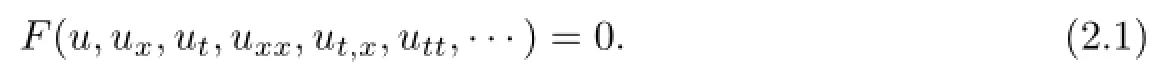
Firstly，we suppose that the traveling solutions of(2.1)with the form u(t，x)=v(η)，η= x+ct or η=x-ct，where c is wave velocity.Substituting these into(2.1)yields the following ordinary differential equation

Secondly，our key step is to assume the solution v that we will find，which satisfies the form

with where b is a parameter，which is to be determined in the following and m can be determined by using the homogeneous balance method(see[3]).Thirdly，substituting(2.3)into(2.2) and making all coefficients of any power of γ equal to zero，then we get a set of algebraic equations for ai，bi，ci(i=1，2，3，···，m).Finally，applying the symbolic computation system“Mathematica”to get the values of the parameters ai，bi，ci(i=1，2，3，···，m)，thus we obtain the exact traveling wave solutions of(2.1).The extended tanh-function method is proposed by Feng[8]for constructing traveling wave solutions of nonlinear partial differential equations in a unified way.The key idea of this method is that γ(η)is the solution of(2.4)satisfying a Riccati equation，i.e.，

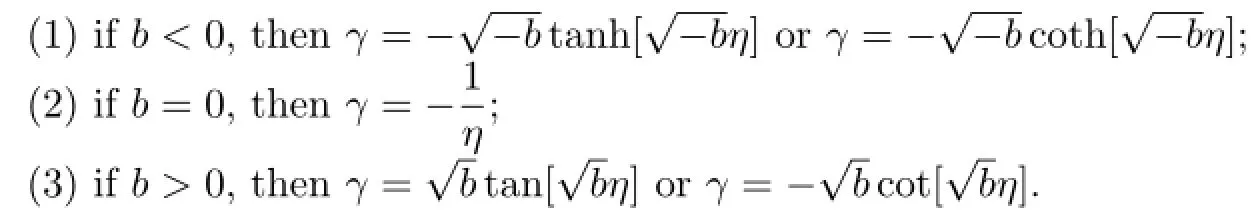
3　The Exact Traveling Wave Solution of Kundu Equation

Suppose that Kundu equation(1.2)has traveling wave solutions as follows:

where η=x-ct，c is a constant.Substituting(3.1)into(1.2)and making the real part and the imaginary part of(1.2)equal to zero，we have

Based on the extended tanh-function method(see[8])，we assume that

where γ(η)satisfies the Riccati equation γ′(η)=b+γ2(η).Applying the homogeneous balance method，through balancing the terms ψ′′ϕ and ψ′ϕ′in(3.2)，we obtain m1=1；and through balancing the terms ϕ4and ψ′ϕ2in(3.3)，we obtain m2=1.Thus we have

Substituting(3.4)and(3.5)into(3.2)and(3.3)，we have

and

Equating each coefficients of power of γ in(3.6)and(3.7)to zero，and then with the help of Mathematica software，we obtain that

and

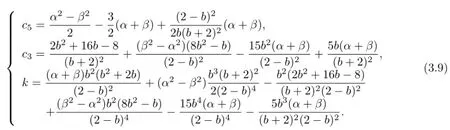
Substituting(3.8)and(3.9)into(3.4)and(3.5)，we find the following traveling wave solutions:

or

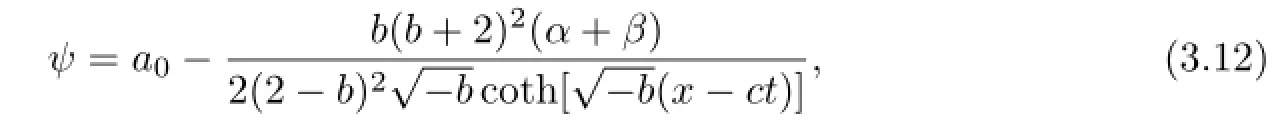
Substituting(3.10)and(3.11)into(3.1)，we have the exact traveling wave solution of(2.1)

where

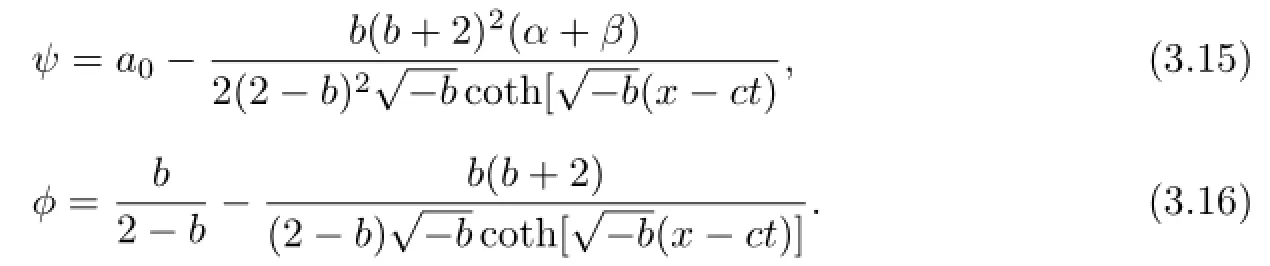
Substituting(3.15)and(3.16)into(3.1)，we have the exact traveling wave solution of equation(2.1)

where k and c are the same as before.

or

Then we obtain the exact traveling wave solutions of(2.1)as follows:

or

or

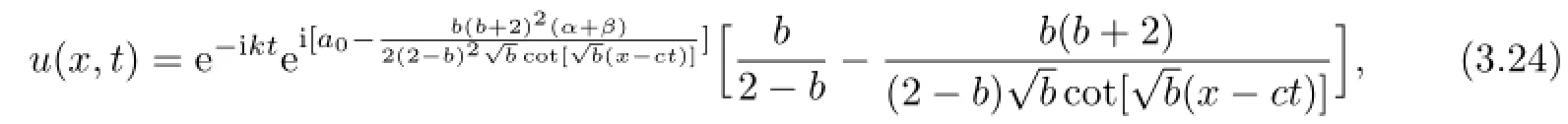
where k and c are the same as before.

Let a0=0，b=-1，α=1 and β=1.Then we haveSubstituting this into (3.10)，(3.11)，(3.12)and(3.13)，we have

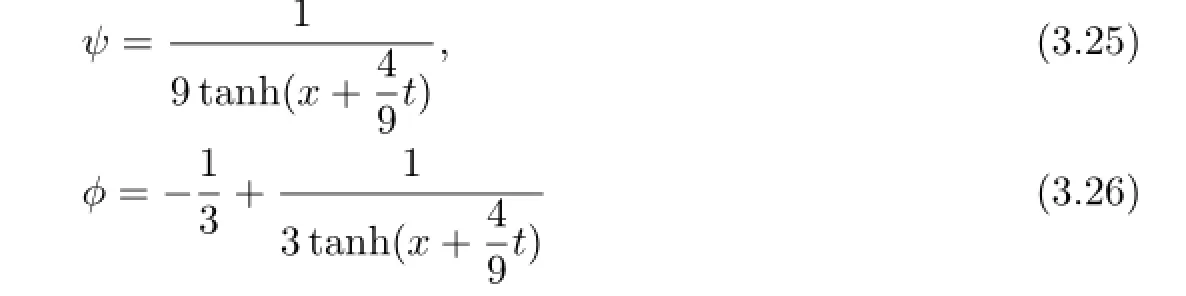
and

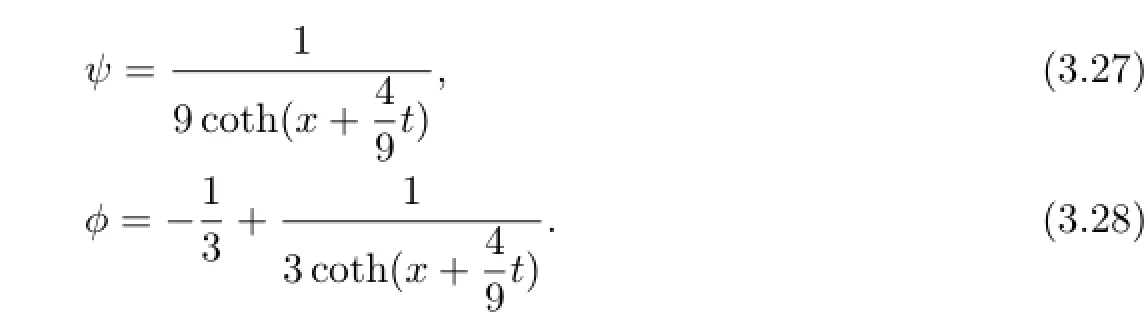
The corresponding pictures of(3.25)，(3.26)，(3.27)and(3.28)are shown in Figs 3.1–3.4.

Fig.3.1

Fig.3.2

Fig.3.3

Fig.3.4

Let a0=0，b=0，α=1 and β=1.Then we have c=0.Substituting this into(3.15) and(3.16)，we have

Let a0=0，b＞0，α=1 and β=1.Then we have c=12.Substituting this into(3.18)，(3.19)，(3.20)and(3.21)，we have

and

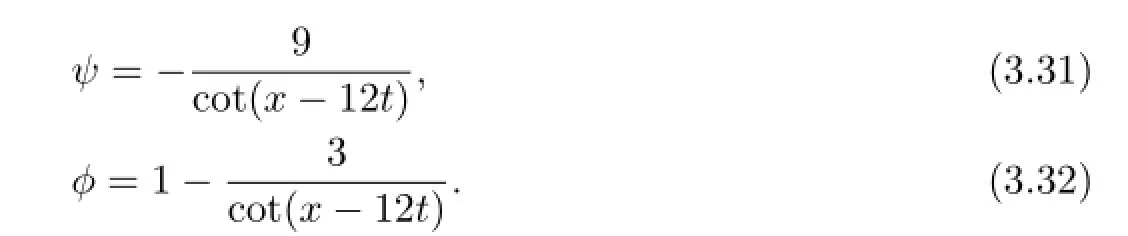
The corresponding pictures of(3.29)，(3.30)，(3.31)and(3.32)are shown in Figs 3.5–3.8.

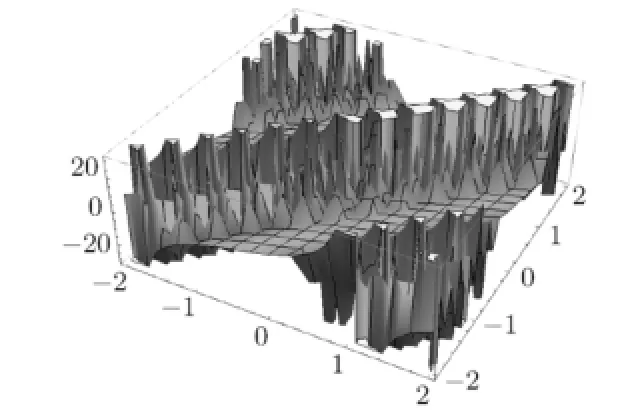
Fig.3.5

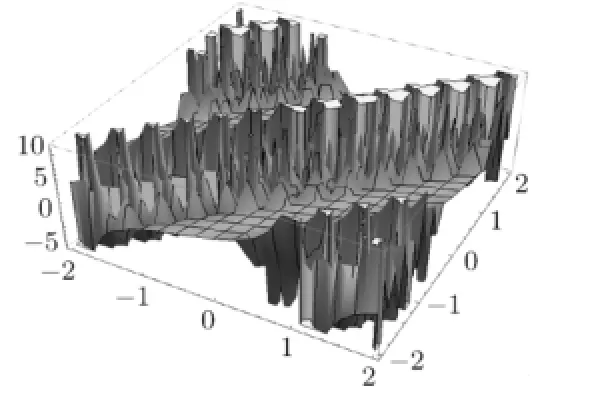
Fig.3.6

Fig.3.7

Fig.3.8

4　Conclusion

Exact traveling wave solutions of nonlinear evolution equation is of important significance for studying the nonlinear phenomena in nature.Because of the complexity of nonlinear evolution equations itself，there is no uniform method to obtain all solutions of nonlinear evolution equation.Fortunately，in soliton theory there have been a series of constructing exact traveling solution method.In view of the different ways，we can see different forms of traveling wave solutions.In this paper，by using the extended tanh-function method and the homogeneous balance method，we obtain the exact traveling wave solutions of Kundu equation with fifth-order nonlinear term.This method is simple and effective and it can be used to other nonlinear evolution equation with higher order.

References

[1]Ablowitz M J，Clarkson P A.Solitons，Nonlinear Evolution Equations and Inverse Scattering. in:London Mathematical Society Lecture Note Series.Cambridge:Cambridge University Press，1991.

[2]Matveev V B，Salle M A.Darboux transformation and solitons.J.Neurochem.，1991，42(6): 1667–1676.

[3]Liu C P.A modified homogeneous balance method and its applications.Commun.Theor. Phys.，2011，56(8):223–227.

[4]Xiao Y F，Xue H L，Zhang H Q.A new extended Jacobi elliptic function expansion method and its application to the generalized shallow water wave equation.J.Appl.Math.，2012，2012(7): 1–18.

[5]Chang J，Liu L H，Gao Y X，Liu B W.Traveling wave solutions of nonlinear evolution equations by improved(G′/G)method(in Chinese).J.Jilin Univ.Sci.，2012，52(3):487–493.

[6]Liu L H，Chang J，Feng X.(G′/G)-expansion method for solving traveling wave solutions of nonlinear evolution equations(in Chinese).J.Jilin Univ.Sci.，2013，51(2):183–186.

[7]Malfliet W.Solitary wave solutions of nonlinear wave equations.Amer.J.Phys.，1992，60(7): 650–654.

[8]Fan E G.Extended tanh-function method and its applications to nonlinear equations.Phys. Lett.A，2000，277(4-5):212–218.

[9]Biswas A.1-soliton solution of the generalized Radhakrishnan，Kundu，Lakshmanan equation. Phys.Lett.A，2009，373(30):2546–2548.

[10]Zhang W，Qin Y，Zhao Y，Guo B.Orbital stability of solitary waves for Kundu equation.J. Differential Equations，2009，247(5):1591–1615.

[11]Taogetusang S.A new exact solution for Kundu equation(in Chinese).J.Inner Mongolia Normal Univ.，2007，36(4):397–401.

10.13447/j.1674-5647.2016.03.10

date:March 21，2016.

The Science Research Plan(Jijiaokehezi[2016]166)of Jilin Province Education Department During the 13th Five-Year Period and the Science Research Starting Foundation(2015023)of Jilin Agricultural University.

E-mail address:caihua@jlu.edu.cn(Cai H).