A Formula for Khovanov Type Link Homology of Pretzel Knots
Zhang Mei-li,Lei Feng-chun,Li Feng-lingand Wang Dong-xu
(1.School of Mathematical Sciences,Dalian University of Technology,Dalian,Liaoning,116024)
(2.Department of Basis,Dalian Naval Academy,Dalian,Liaoning,116018)
(3.Mathematics Department,Dongbei University of Finance and Economics,Dalian,Liaoning,116025)
A Formula for Khovanov Type Link Homology of Pretzel Knots
Zhang Mei-li1,2,Lei Feng-chun1,*,Li Feng-ling1and Wang Dong-xu3
(1.School of Mathematical Sciences,Dalian University of Technology,Dalian,Liaoning,116024)
(2.Department of Basis,Dalian Naval Academy,Dalian,Liaoning,116018)
(3.Mathematics Department,Dongbei University of Finance and Economics,Dalian,Liaoning,116025)
Khovanov type homology is a generalization of Khovanov homology. The main result of this paper is to give a recursive formula for Khovanov type homology of pretzel knotsP(−n,−m,m).The computations reveal that the rank of the homology of pretzel knots is an invariant ofn.The proof is based on a“shortcut”and two lemmas that recursively reduce the computational complexity of Khovanov type homology.
pretzel knot,Khovanov type homology,Frobenius algebra,TQFT
2010 MR subject classification:57M25,57M27,16W30
Document code:A
Article ID:1674-5647(2016)03-0198-09
1 Introduction
Khovanov homology[1]is a modern and powerful invariant for knots and links related to the representation theory,physics,and symplectic geometry.As a graded homology theory,it is a categorification of the Jones polynomial.In[2],a new homology theory of knots and links over a ring R,Khovanov type homology,is constructed from a Frobenius algebra,and its corresponding geometric interpretation is obtained.The link homology theory is different from the known natural generalizations(see[3]–[7]).
It is well known that the 3-strand pretzel knots are well-studied sources of examples in the knot theory.Khaled[8]proved a recursion formula for the rational Khovanov homologyof families of pretzel links P(p,r,r).Suzuki[9]calculated the rational Khovanov homology of a class of pretzel knots P(p,q,r)by using the spectral sequence constructed by Turner[10]. Manion[11]gave a formula for the unreduced Khovanov homology over the rational numbers of all 3-strand pretzel links.However,computing the generalized Khovanov homology over R remains mysterious in many cases.
In this paper,we set out to calculate Khovanov type homology of infinite classes of knots,pretzel knots P(-n,-m,m).We utilize the simplicity of the diagrams resulting from resolving one of the crossings to make an inductive argument in terms of n.Thus,we provide a recursive formula for Khovanov type homology of pretzel knots.
The organization of the coming sections is as follows.In Section 2,we give a brief summary of Khovanov type homology and review a computational shortcut to Khovanov homology.Similarly,we can use the“shortcut”to calculate Khovanov type homology.In Section 3,after proving two lemmas of Khovanov type homology,we obtain a formula for pretzel knots P(-n,-m,m).
2 Preliminary
2.1Khovanov Type Homology
For a ring R,a(1+1)topological quantum field theory(TQFT for short,see[12]–[13])which is a functor on(1+1)cobordisms(see[5])valued in the category R-module has been studied in[1].
The authors firstly construct a Frobenius algebra(see[14]),which is a free R-module over the basic ring of rank 2 generated by 1 and x.
To get a algebra structure,a multiplication m:A⊗A→A is given by
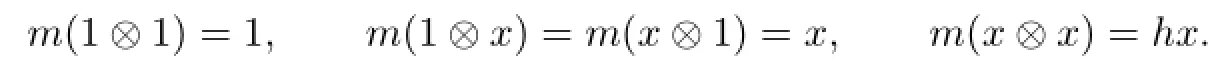
For simplification,we abbreviate x⊗x=hx by x2=hx,where h∈R and hn−1=0 which implies that xn=0 for n≥3.
To get a coalgebra structure,a comultiplication∆:A→A⊗A is given by
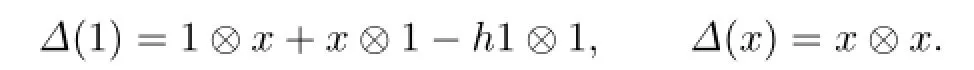
We introduce a Z-grading on R by deg(h)=-2,deg(1)=1,deg(x)=-1.
Consequently,given a link diagram D,the cube of resolutions is built from it,where vertices of the cube are of all possible 0 and 1 resolutions of the crossings.The resolutions are represented by the Kauffman states(see[15])themselves as shown in Fig.2.1.The edges of the cube are certain given surfaces to which the appropriate signs are attached. The entire cube is“summed”into a chain complex,¯C(D),in the appropriate geometric category.
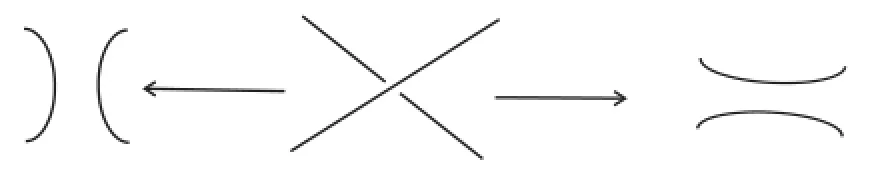
Fig.2.1The resolution 0 and 1 of a crossing
By TQFT,the homology of the chain complex is bigraded modules.Since it is independent of the choice of a link diagram,it defines an invariant of oriented links.
Let
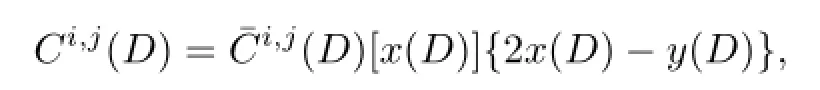
where x(D)and y(D)are the numbers of negative crossings and positive crossings of D,respectively.We denote(D)and Hi,j(D)to be the homology group of the complex(D)and Ci,j(D),respectively.We have
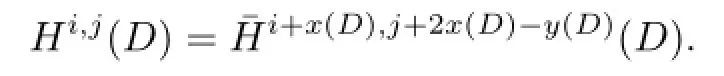
2.2A Computational Shortcut to Khovanov Type Homology
We introduce a computational shortcut that was discovered by Khovanov in[3].Let D be a knot diagram with n crossings that contains a subdiagram picture below.
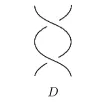
Fig.2.2A double left twist as part of a knot diagram D
We resolve two crossings of D to obtain D(∗00),D(∗01),D(∗10)and D(∗11)as shown in Fig.2.3.
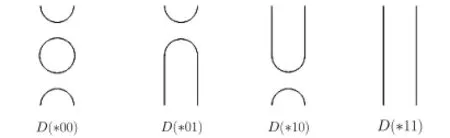
Fig.2.3The four possible resolutions of the double left twist
It is clear that D(∗01)and D(∗10)are isomorphic,and D(∗00)is isomorphic to the union of D(∗01)and a simple circle.To simplify,let D0=D(∗01)and D1=D(∗11).
Let C be the complex
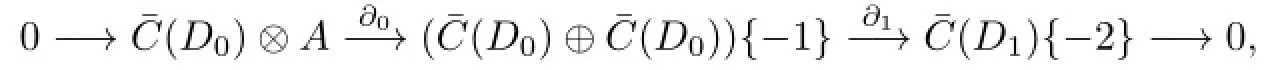
CSbe the subcomplex
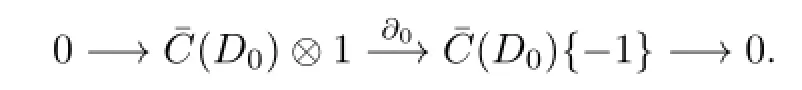
We define the following maps:

and
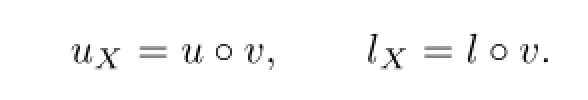
We have
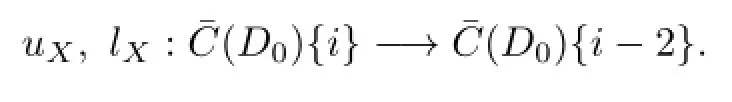
Lemma 2.1[2]The bicomplex C/CSis isomorphic to the bicomplex
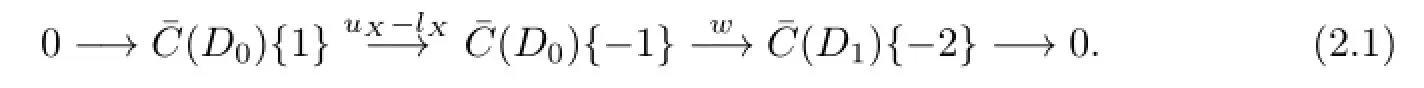
Corollary 2.1The homology groups¯Hi(D)are isomorphic to the homology of the total complex of the bicomplex(2.1).
3 Khovanov Type Homology of Pretzel Knots P(-n,-m,m)
We firstly present two lemmas that reduce the computational difficulty of Khovanov type homology Hi(D).Then we use the lemmas and the“shortcut”to compute the homology groups of pretzel knots P(-n,-m,m)as shown in Fig.3.1.The following images are sourced from[16].
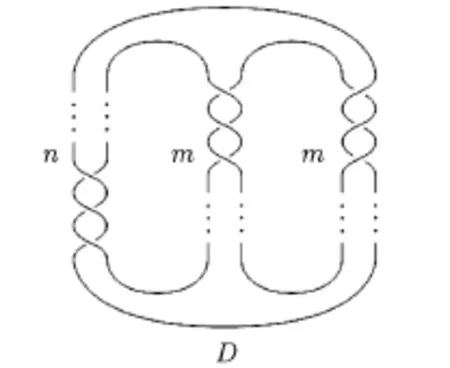
Fig.3.1The pretzel knots P(−n,−m,m)
Lemma 3.1In pretzel knots P(-n,-m,m),to a left twist,the generators of the homology groups are only nontrivial in the 0-resolution of the left twist.
Proof.To a left twist,we resolve the crossing to obtain D0and D1as shown in Fig.3.2.
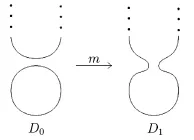
Fig.3.2The left twist complex
Lemma 3.2The set of crossings is shown in Fig.3.3(1),the generators of the homology groups are only nontrivial in the following resolution as shown in Fig.3.3(2).
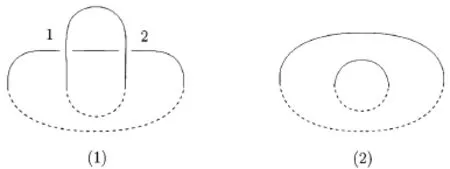
Fig.3.3The set of crossings
Proof.We resolve the two crossings as shown in Fig.3.3(1).The four possible resolutions get the cube as shown in Fig.3.4.
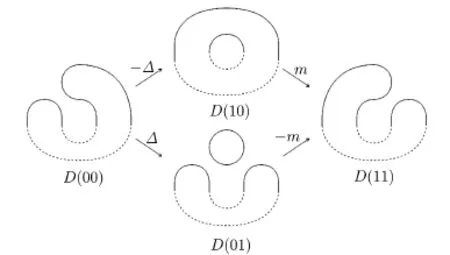
Fig.3.4The four possible resolutions
Therefore,we obtain the complex

Since ker(-∆,∆)is trivial and Imcontributes to the homology.
Since
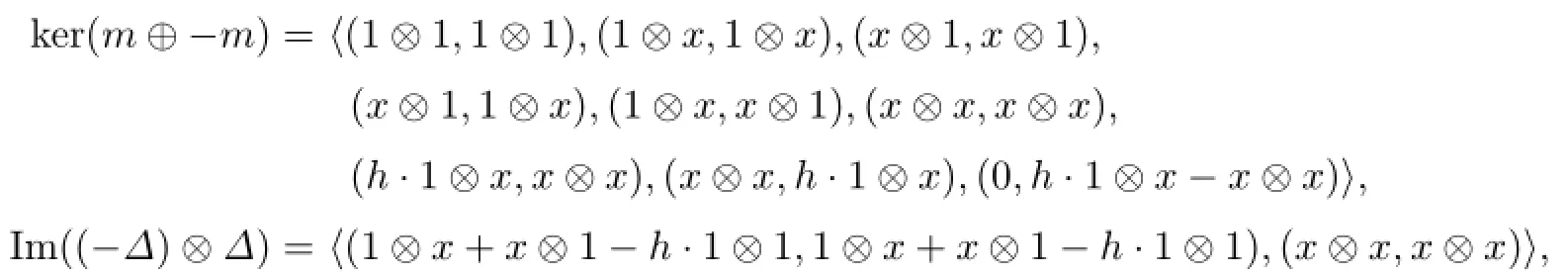
we have
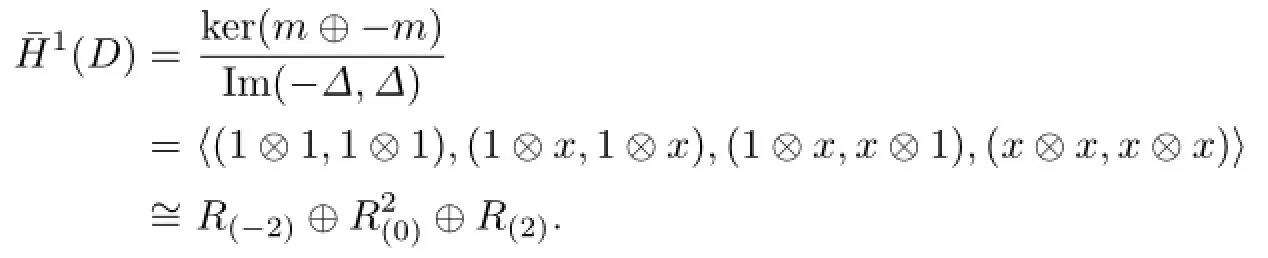
It is easy to see that
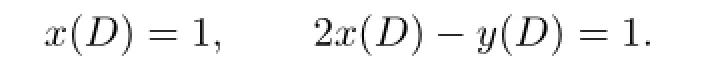
Because{-1}occurs after one 1-resolution,we have

Therefore,we see that all four generators live in¯C(D(10))as shown in Fig.3.3(2).
Next we give and prove the main result.
Theorem 3.1For pretzel knots P(-n,-m,m)as shown in Fig.3.1,Khovanov type homology Hi(P(-n,-m,m))is given by

Proof.Let D be the knot diagram of P(-n,-m,m).We resolve two crossings in the double left twists.By(2.1),we only need to calculate the bicomplex
where D0and D1are the knot diagrams of 0 and 1-resolutions to the double left twists in P(-n,-m,m),see Fig.3.5.
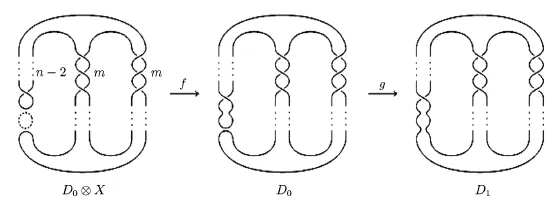
Fig.3.5The maps between complexes after the resolution of the double left twist
Note that D0is equivalent to the unlink of two components,and D1is equivalent to P(-(n-2),-m,m).According to Lemma 3.1,each of the crossings in the left twists in D0only needs to be resolved with the 0-resolution.Each of the crossings in the remaining two pairs of twists needs only to be resolved as specified in Lemma 3.2.Therefore,for all the possible resolutions of D0,there is a unique resolution that contains all the generators that contribute to the homology.That is,D0has n-2 left twists that should be resolved with0-resolutions,and m pairs of left and right twists that must be resolved with pairs of 1 and 0-resolutions as shown in Fig.3.6.
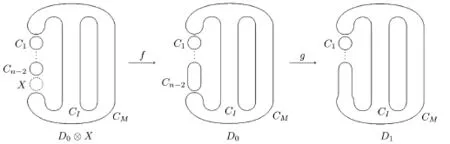
Fig.3.6The maps between the pertinent resolutions of D
Resolving D0gives us n-2 small circles Ci(i=1,2,···,n-2).In D0⊗X,there is the inherent circle X.Being left to be labeled are CMand CI.
It is clear that f combined with absorption into the circle Cn−2is the absorption of the circle X into CM.According to TQFT,we assign R-module A to a circle.Then
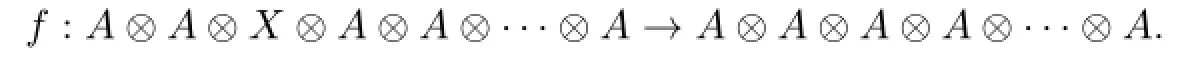
By Lemma 2.1,f is defined by
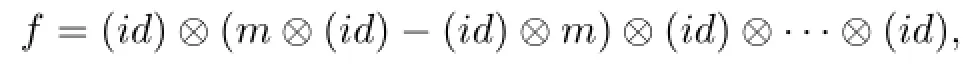
where m is multiplication by X.In order for an element to be in the kernel of f,it must have X in both the CMand Cn−2components,as well.The only component that can vary in the kernel is CI.Therefore,the kernel and the image in D0⊗X are given by
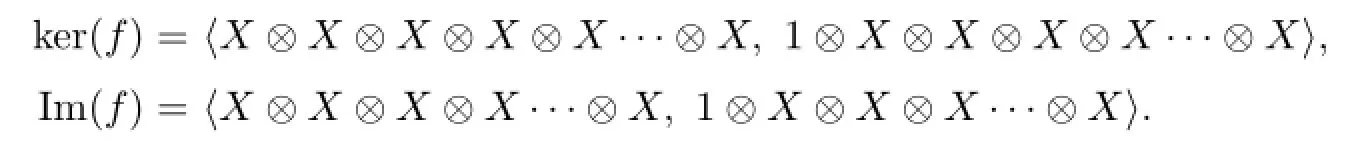
Then
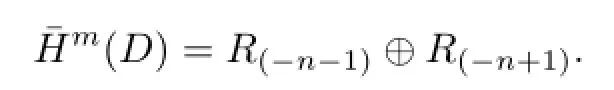
Now we can look at what shifts should be applied.
There are homological and grading shifts of[m]{m-n}from the number of right and left twists in the original diagram D,and there is a grading shift of{-m}because there are m 1-resolutions in the diagram.Therefore,
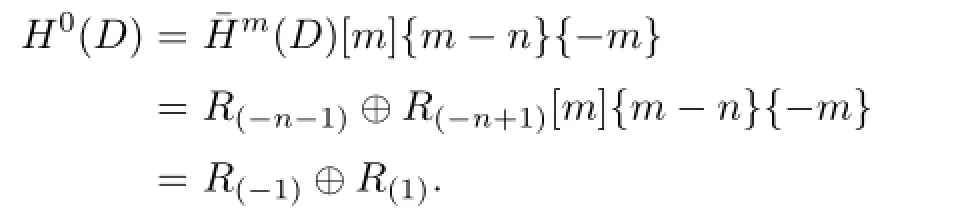
In C(D0),we note that the function g acts as multiplication of Cn−2on CMand Cn−3,therefore,
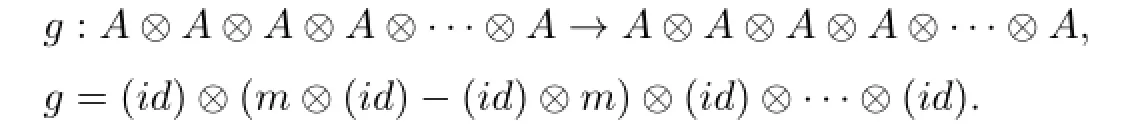
The kernel of g has the X on every component with the exception that CIcan be represented by either X or 1.This means that ker(g)=Im(f),so there is no contribution to the homology in the complex,that is,H1(D)=0.
Next,we compute H2(D).
Note that

However,not all these elements kill off generators in the homology,as some may already be 0 due to the homomorphism h:as shown in Fig.3.7.
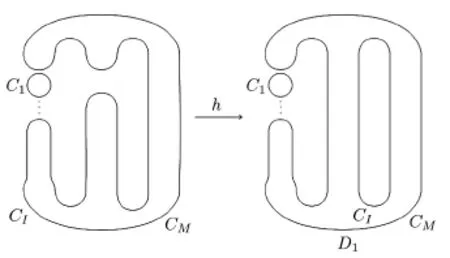
Fig.3.7The map h
Since
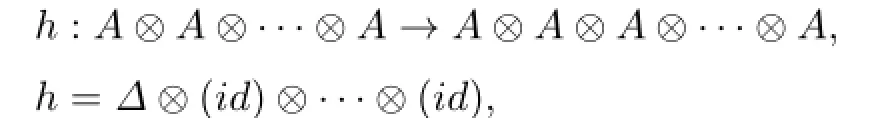
we get
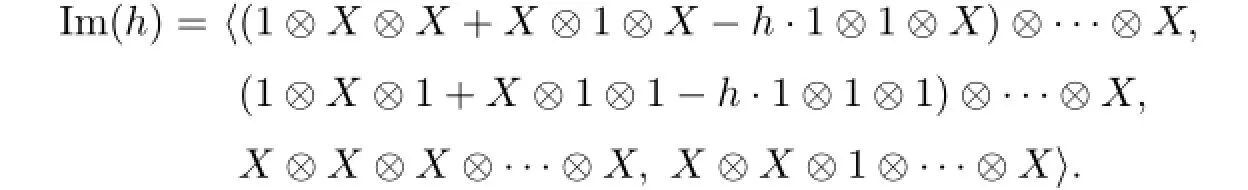
When we reduce the image of g by the image of h,we see that the precise effect of g on the homology here is to reduce the homology.In fact,
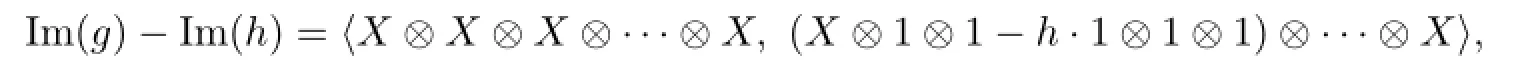
so

Since x(D1)=m-2,2x(D1)-y(D1)=m-n+2 and a shift of{-m-2}for the number of 1-resolutions,g kills precisely the following groups from the contribution of C(D1). Therefore,
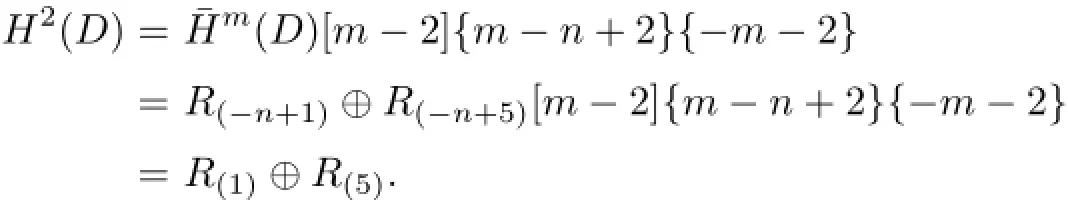
Note that D and D1are denoted to the diagram P(-n,-m,m)and P(-(n-2),-m,m) respectively,so there is a shift of[-2]{-4}between C(D)and C(D1).Therefore,
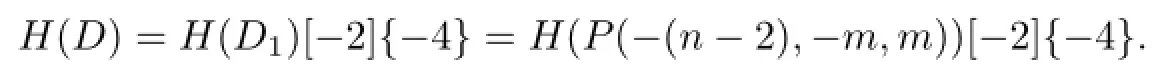
Thus it has been shown that in general,Khovanov type homology of P(-n,-m,m)is Khovanov homology of P(-(n-2),-m,m),shifted,with an addition of R(−1)⊕R(1)in the 0-th homology and the moding out R(1)⊕R(5)from the 2nd homology.The proof is completed.
Throughout this iteration,we have the following corollary.
Corollary 3.1The rank of the Khovanov type homology to the pretzel knots P(-n,-m,m) is an invariant of n.
References
[1]Khovanov M.A categorification of the Jones polynomial.Duke Math.J.,2000,101:359–426.
[2]Zhang M L,Lei F C.A Khovanov type link homology with geometric interpretation.Acta Math.Sin.(Engl.Ser.),2016,32(4):393–405.
[3]Khovanov M.Link homology and Frobenius extensions.Fund.Math.,2006,190:179–190.
[4]Bar-Natan D.On Khovanov’s categorification of the Jones polynomial.Algebr.Geom.Topol.,2002,2:337–370.
[5]Bar-Natan D.Khovanov’s homology for tangles and cobordisms.Geom.Topol.,2005,9:1443–1499.
[6]Turner P.Calculating Bar-Natan’s characteristic two Khovanov homology.J.Knot Theory Ramifications,2006,10:1335–1356.
[7]Naot G.The universal Khovanov link homology theory.Algebr.Geom.Topol.,2006,6:1863–1892.
[8]Khaled Q.The Khovanov homology of a family of three-column pretzel links.Commun.Contemp.Math.,2011,13:813–825.
[9]Suzuki R.Khovanov homology and Rasmussen’s s-invariants for pretzel knots.J.Knot Theory Ramifications,2010,19:1183–1204.
[10]Turner P.A spectral sequence for Khovanov homology with an application to(3,q)-torus links. Algebr.Geom.Topol.,2008,8:869–884.
[11]Manion A.The rational Khovanov homology of 3-strand pretzel links.J.Knot Theory Ramifications,2014,23:1450040,1–40.
[12]Bursos Soto H,Hu´erfano S.Khovanov type homologies and Frobenius extension.Lect.Mat.,2006,27:57–83.
[13]Kock J.Frobenius algebra and 2D topological quantum field theories.London Mathematical Society Student Texts,59,Cambridge:Cambridge University Press,2004.
[14]Abrams L.Two-dimensional topological quantum field theories and Frobenius algebra.J.Knot Theory Ramifications,1996,5:569–587.
[15]Kauffman L.H.State models and the Jones polynomial.Topology,1987,26:395–407.
[16]Jeffrey M.A recursive formula for the Khovanov cohomology of a family of 3-stranded pretzel knots.a thesis of Science in Mathematics.University of Nevada,Reno,USA.UMI No.1464452,2009,1–33.
10.13447/j.1674-5647.2016.03.02
date:Nov.23,2015.
The NSF(11329101,11431009,11471151 and 11401069)in part,and the Fundamental Research Funds(DUT14LK12)for the Central Universities.
*Corresponding author.
E-mail address:zhangmeili66@sina.com(Zhang M L),fclei@dlut.edu.cn(Lei F C).
 Communications in Mathematical Research2016年3期
Communications in Mathematical Research2016年3期
- Communications in Mathematical Research的其它文章
- On Non-commuting Sets in a Finite p-group with Derived Subgroup of Prime Order
- Measures of Asymmetry Dual to Mean Minkowski Measures of Asymmetry for Convex Bodies
- Stochastic Maximum Principle for Optimal Control of Forward-backward Stochastic Pantograph Systems with Regime Switching
- Common Fixed Point Theorems and Q-property for Quasi-contractive Mappings under c-distance on TVS-valued Cone Metric Spaces without the Normality
- A Class of Ruin Probability Model with Dependent Structure
- Existence and Uniqueness of Positive Solutions for a System of Multi-order Fractional Differential Equations
