Common Fixed Point Theorems and Q-property for Quasi-contractive Mappings under c-distance on TVS-valued Cone Metric Spaces without the Normality
Piao Yong-jie
(Department of Mathematics,College of Science,Yanbian University,Yanji,Jilin,133002)
Communicated by Ji You-qing
Common Fixed Point Theorems and Q-property for Quasi-contractive Mappings under c-distance on TVS-valued Cone Metric Spaces without the Normality
Piao Yong-jie
(Department of Mathematics,College of Science,Yanbian University,Yanji,Jilin,133002)
Communicated by Ji You-qing
Fixed point and common fixed point results for mappings satisfying quasicontractive conditions expressed in the terms of c-distance on TVS-valued cone metric spaces(without the underlying cone which is not normal)are obtained,and P-property and Q-property for mappings in the terms of c-distance are discussed.Our results generalize and improve many known results.
TVS-valued cone metric space,quasi-contractive condition,common fixed point,P-property,Q-property
2010 MR subject classification:47H05,47H10,54E40,54H25
Document code:A
Article ID:1674-5647(2016)03-0229-12
1 Introduction and Preliminaries
Huang and Zhang[1]have introduced the concepts of cone metric spaces,where the set of real numbers is replaced by an order Banach space.Du et al.[2]–[10]discussed the existence problems of fixed points and common fixed points for mappings defined on TVS-valued cone metric spaces,where the order Banach space is replaced by a topological vector space.
Fixed point results in metric spaces with the so-called w-distance were obtained for the first by Kada et al.[11],where non-convex minimization problems were treated.Further results were given in[12]–[14].The cone metric version of this notion(usually called a c-distance)was used in[15]–[16].
Wang and Guo[17]obtained a fixed point theorem for a mapping in normal cone metricspace under some contractive condition expressed in the terms of c-distance,and Djordjevi´c et al.[18]also obtained fixed point and common fixed point results for mappings in TVS-valued non-normal cone metric spaces under contractive condition expressed in the terms of c-distance.Those results generalize the corresponding results in[11]–[16]and the related results.
Here,we discuss the existence problems of fixed points and common fixed points for mappings on TVS-valued non-normal cone metric spaces under quasi-contractive condition expressed in the terms of c-distance and P-property and Q-property.The obtained results generalize the conclusions in[17]–[18]and other corresponding fixed point and common fixed point theorems.
Let(E,τ)be a topological vector space(TVS),P0a nonempty subset of E.P0is said to be a cone whenever
(i)P0is closed,nonempty and
(ii)ax+by∈P0for all x,y∈P0and real numbers a,b≥0;
(iii)P0∩(-P0)={0}.
In this paper,we always assume that the cone P0has a nonempty interior,i.e.,int(such cones are called solid).
For a given cone P0⊂E,we define a partial ordering≤with respect to P0by x≤y if and only if y-x∈P0.x<y stands for x≤y andx≪y stands for y-x∈intP0.
A cone P0is called normal if there exists a real number K>0 such that for all x,y∈E,
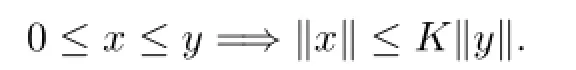
The least positive number K satisfying the above condition is called the normal constant of P0.
It is known that a metric space is a normal cone metric space with normal constant K=1.
Definition 1.1Let X be a nonempty set and E a TVS with solid cone P0.Suppose that the mapping d:X×X→E satisfies
(1)0≤d(x,y)for all x,y∈X,and d(x,y)=0 if and only if x=y;
(2)d(x,y)=d(y,x)for all x,y∈X;
(3)d(x,y)≤d(x,z)+d(z,y)for all x,z,y∈X.
Then d is called a TVS-valued cone metric on X,(X,d)is called a TVS-valued cone metric space.
Definition 1.2Let(X,d)be a TVS-valued cone metric space,x∈X and{xn}n∈N+a sequence in X.Then
(1){xn}is a Cauchy sequence whenever for every c∈E with 0≪c there exists an N∈N+such that d(xm,xn)≪c for all n,m>N;
(2){xn}converges to x whenever for every c∈E with 0≪c,there exists an N∈N+such that d(xn,x)≪c for all n>N.We denote this by
(3)(X,d)is called complete if every Cauchy sequence in X is convergent.
We shall make use of the following properties:
(P1)If u,v,w∈E,u≤v and v≤w,then u≤w.
(P2)If u≤λu,where u∈P0and 0≤λ<1,then u=θ.
Definition 1.3Let(X,d)be a TVS-valued cone metric space.A function q:X×X→E is called a c-distance on X,if
(1)θ≤q(x,y)for all x,y∈X;
(2)q(x,z)≤q(x,y)+q(y,z)for all x,y,z∈X;
(3)a sequence{yn}in X converges to a point y∈X,and for some x∈X and u=ux∈P0,q(x,yn)≤u holds for each n∈N+,then q(x,y)≤u;
(4)for each c∈E with θ≪c,there exists an e∈E with θ≪e such that q(z,x)≪e and q(z,y)≪e implies d(x,y)≪c.
The following facts can be found in[17]–[18].
1.Every w-distance must be a c-distance on TVS-valued cone metric spaces.
2.There are many examples of c-distances on TVS-valued cone metric spaces but not c-distance on cone metric spaces,see[11].
3.For c-distance q,
1)q(x,y)=q(y,x)does not necessarily hold for all x,y∈X;
2)q(x,y)=0 is not necessarily equivalent to x=y.
Definition 1.4A sequence{un}in P0is said to be a c-sequence if for each c≫0 there exists an n0∈N+such that un≪c for all n≥n0.
Obviously,if{un}and{vn}are c-sequences in E and α,β>0,then{αun+βvn}is a c-sequence.
Definition 1.5Let(X,d)is a TVS-valued cone metric space,f:X→X a mapping and x0∈X.If for each c∈E with c≫0,there exists a b∈E with b≫0 such that x∈X,d(x,x0)≪b implies d(fx,fx0)≪c,then we say that f is continuous at x0.f is said to be continuous on X if f is continuous at every x∈X.
Lemma 1.1[18]Let(X,d)be a TVS-valued cone metric space,q a c-distance on X. Suppose that{xn}and{yn}are two sequences in X and x,y,z∈X.If{un}and{vn}are two c-sequences in P0,then the following properties hold:
(1)If q(xn,y)≤unand q(xn,z)≤vnfor any n∈N+,then y=z.In particular,if q(x,y)=0 and q(x,z)=0,then y=z.
(2)If q(xn,xm)≤unfor all m>n>n0,then{xn}is a Cauchy sequence in X.
Adopting the proof process of Lemma 2 in[19],we can obtain the following result:
Lemma 1.2Let(X,d)be a TVS-valued cone metric space,f:X→X a mapping and x0∈X.Then f is continuous at x0if and only if xn→x0as n→∞implies fxn→fx0as n→∞.
2 Fixed Points and Common Fixed Points under c-distance
Theorem 2.1Let(X,d)be a complete TVS-valued cone metric space,q be a c-distance,m and n be two positive integers.Suppose that two mappings f,g:X→X are commutable,fmand gnare both onto and continuous.If for every x,y∈X,
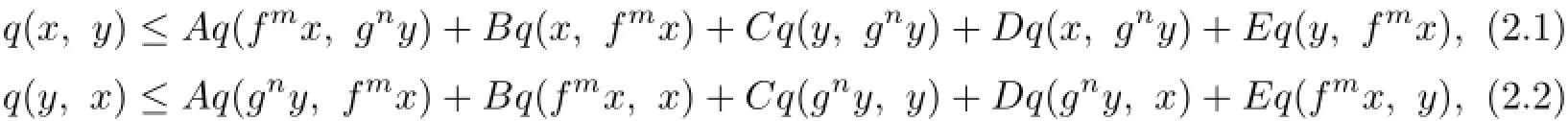
where A,B,C,D,E≥0 and A+B+C+2D+2E<1,then f and g have a unique common fixed point u∈X with q(u,u)=0.
Proof.By the subjectivity of fmand gn,we take x0∈X and constructsatisfying
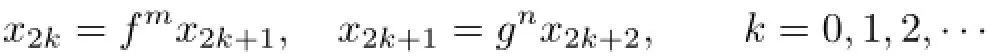
For any k=0,1,2,···,by(2.1)and(2.2)respectively,one has

Let
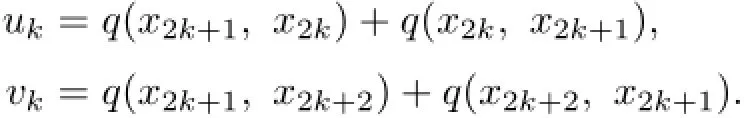
Adding up(2.3)and(2.4),we obtain

Similarly,by(2.2)and(2.1)respectively,we obtain
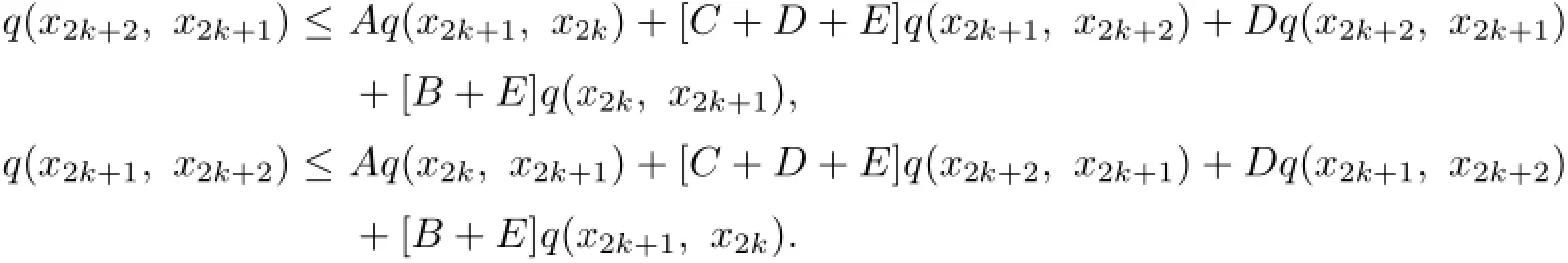
Adding up the above two formulas,we obtain

Let h=h1h2.Then 0<h<1.And from(2.5)and(2.6),we obtain
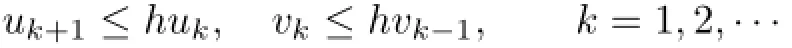
Hence,by using the mathematical induction,we obtain
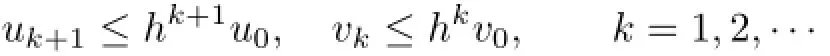
Since q(x2k,x2k+1)≤ukand q(x2k+1,x2k+2)≤vk,so
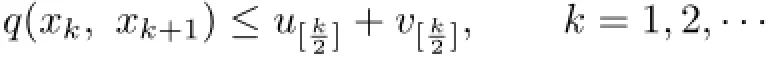
Hence,for any α,β∈N+with β>α≥1,
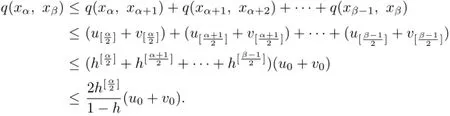
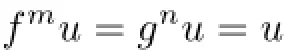
by the continuity of fmand gn.
In view of(2.1),
q(u,u)≤Aq(fmu,gnu)+Bq(u,fmu)+Cq(u,gnu)+Dq(u,gmu)+Eq(u,fmu) =[A+B+C+D+E]q(u,u),
hence
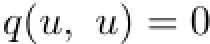
by(P2)(since 0<A+B+C+D+E<A+B+C+2D+2E<1).
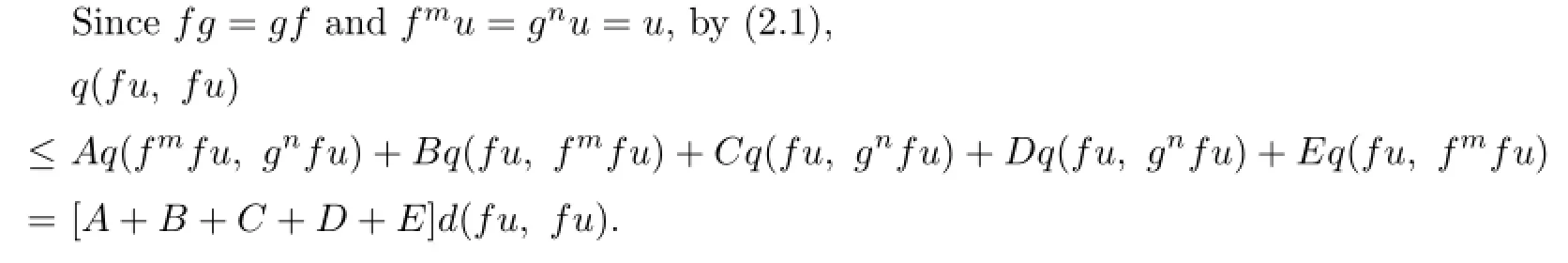
Hence,by(P2),
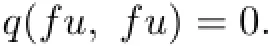
Similarly,we have
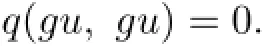
By using(2.1)and(2.2)respectively,we obtain the following two conclusions:
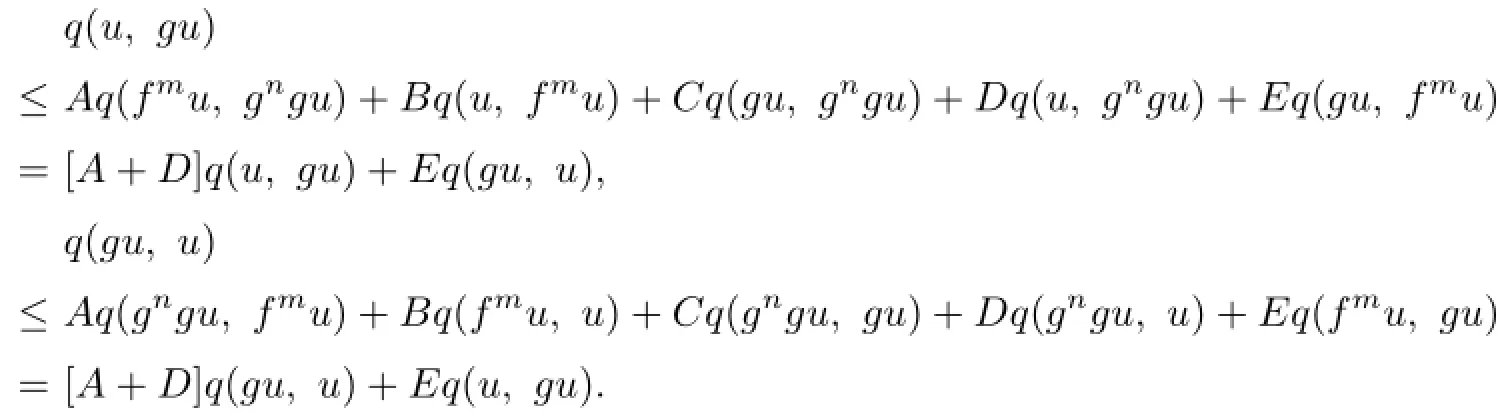
Adding up the above two formulas,we obtain
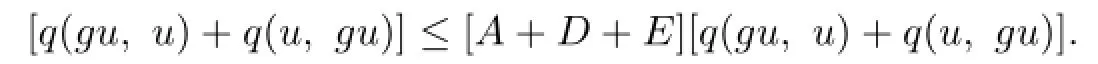
Hence
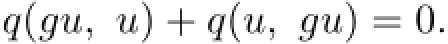
So
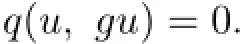
But q(u,u)=0,hence,by Lemma 1.1(1),
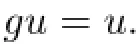
Similarly,by using(2.1)and(2.2)respectively,we obtain
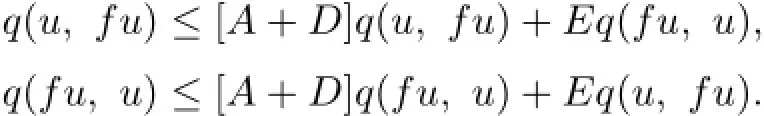
Adding up the two formulas,we obtain
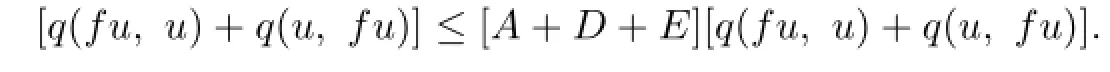
Hence
and therefore
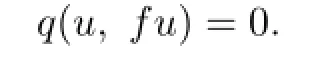
So
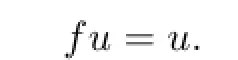
Thereby u is a common fixed point of f and g.
If v is a common fixed point of f and g,then by(2.1)and(2.2)respectively,

Adding up the two above,we obtain
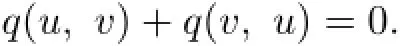
Hence
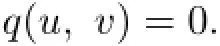
Therefore,by Lemma 1.1(1),u=v.The proof is completed.
The following results is a particular form of Theorem 2.1.
Theorem 2.2Let(X,d)be a complete TVS-valued cone metric space,q be a c-distance,m and n be two positive integers and α,β,γ≥0.Suppose that two mappings f,g:X→X are commutable,fmand gnare both onto and continuous.If for every x,y∈X,
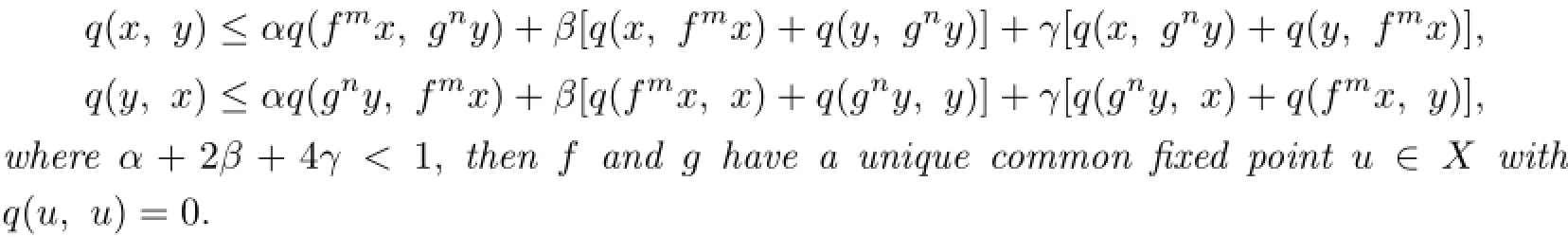
Proof.Let A=α,B=C=β,D=E=γ.Then the conclusion follows from Theorem 2.1.
Next,we give the non-commutable version of Theorem 2.1.
Theorem 2.3Let(X,d)be a complete TVS-valued cone metric space,q be a c-distance,m and n be two positive integers.Suppose that two mappings f,g:X→X satisfy that fmand gnare both onto and continuous.If(2.1)and(2.2)hold for every x,y∈X,where A,B,C,D,E≥0 with A+2B+2C+2D+2E<1,then f and g have a unique common fixed point u∈X with q(u,u)=0.
Proof.Just as the proof of Theorem 2.1,there exist a Cauchy sequence{xn}and an element u∈X satisfying xn→u as n→∞and fmu=gnu=u with q(u,u)=0.
By(2.1)and(2.2)respectively,we have
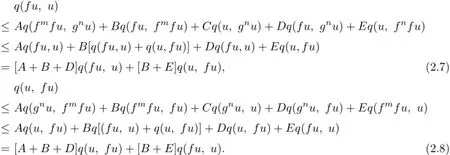
Adding up(2.7)and(2.8),we obtain
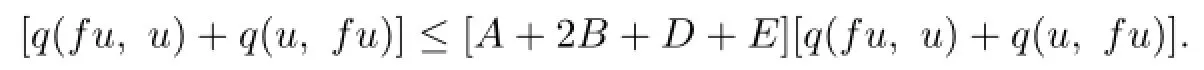
Hence
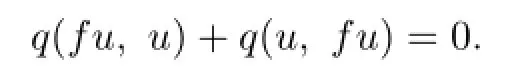
So
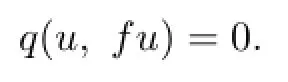
Therefore,
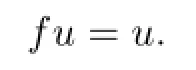
Similarly,by(2.1)and(2.2)respectively,we have
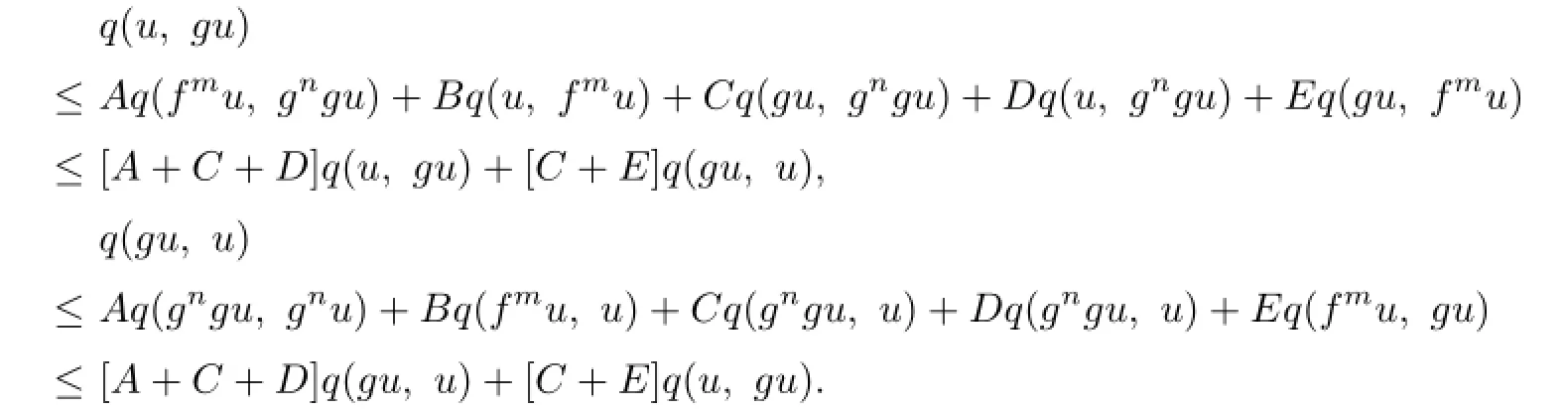
Adding up the above two formulas,we have
Hence
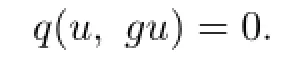
Therefore,
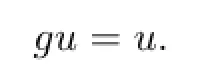
So u is a common fixed point of f and g.
The rest is similar to the proof of Theorem 2.1.The proof is completed.
The following result is a particular case of Theorem 2.3 and also a non-commutable version of Theorem 2.2.
Theorem 2.4Let(X,d)be a complete TVS-valued cone metric space,q be a c-distance,m and n be two positive integers and α,β,γ≥0.Suppose that two mappings f,g:X→X satisfy that fmand gnare both onto and continuous.If for every x,y∈X,
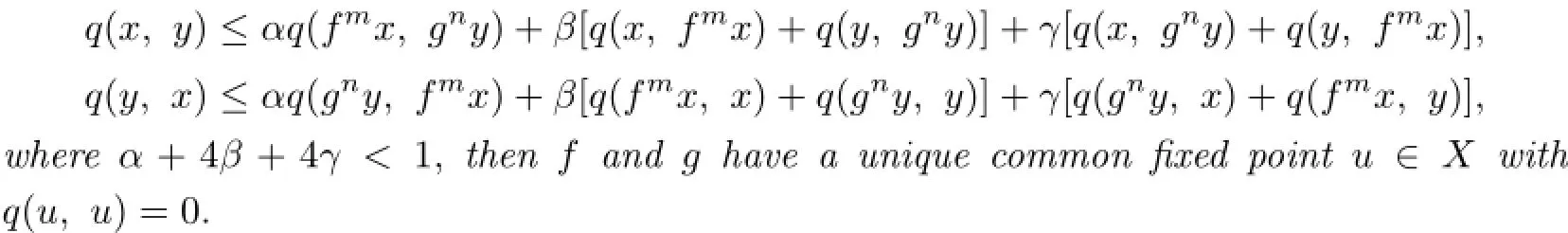
3 Another Class of Common Fixed Point and P(Q)-property
A mapping f:X→X is said to have P-property if f satisfies
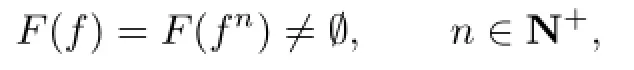
where F(f)denotes the set of fixed points of f.Two mappings f,g:X→X are said to have Q-property if f,g satisfy
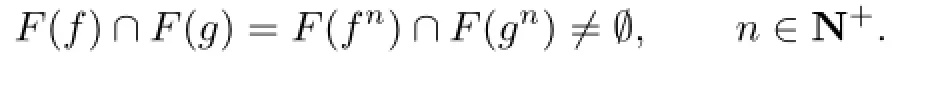
Theorem 3.1Let(X,d)be a complete TVS-valued cone metric space,q be a c-distance. Suppose that two onto and commutable and continuous mappings f,g:X→X satisfy
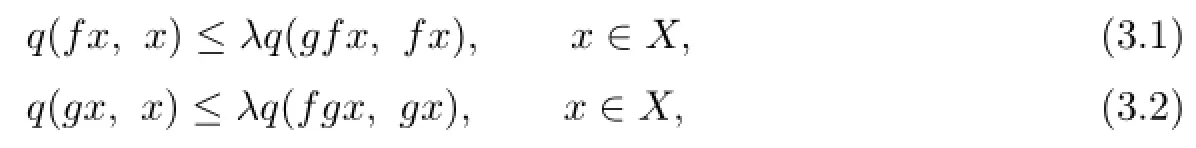
where λ∈(0,1).Then f and g have a common fixed point u∈X with q(u,u)=0 and Q-property.
Proof.Take x0∈X and construct a sequencesatisfying

For any n=1,2,···,by using(3.1)and(3.2)respectively,we obtain
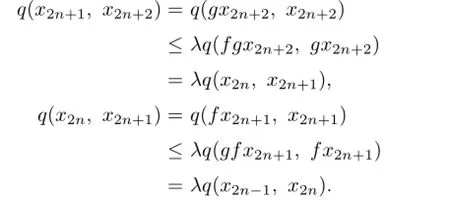
Hence,by the mathematical induction,
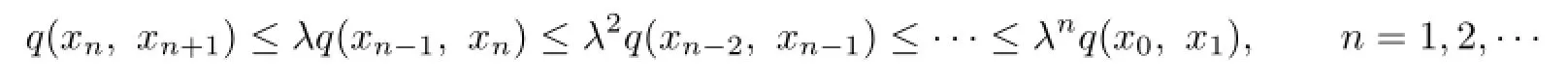
Therefore,for any m>n≥1,
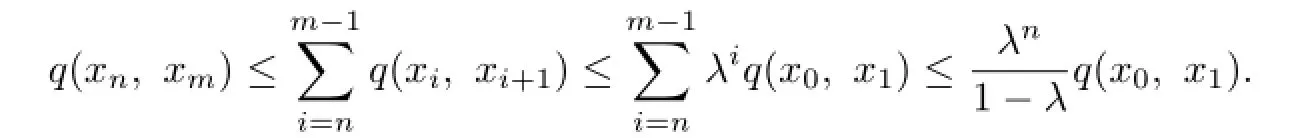
So{xn}is Cauchy by Lemma 1.1(2).Hence,there is a u∈X such that xn→u as n→∞by the completeness of X.Therefore
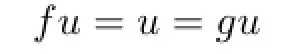
by the continuity of f and g,i.e.,F(f)∩F(g)̸=∅.
Since
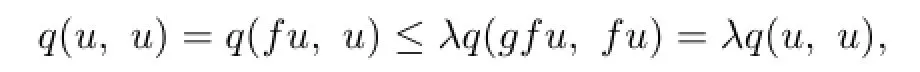
we know q(u,u)=0 by(P2).
Obviously,
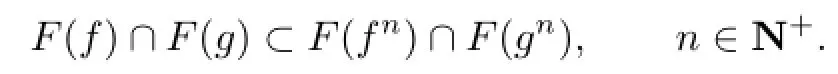
Fix any n∈N+and take u∈F(fn)∩F(gn).For any k=1,2,···,n,by(3.1)and(3.2),we have
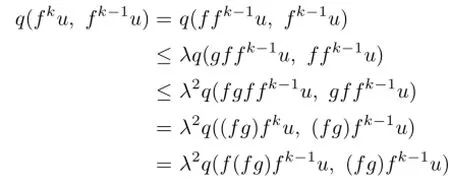
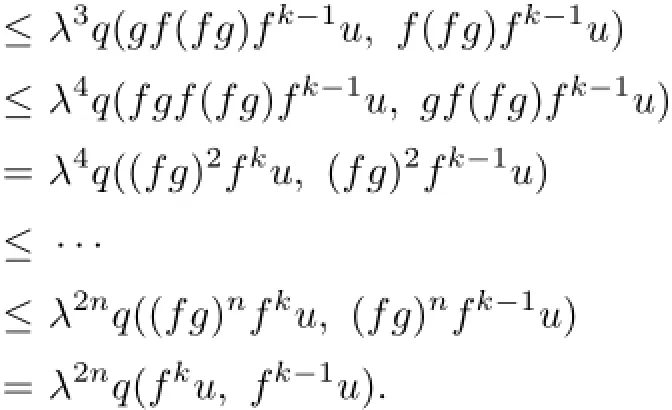
Hence,by(P2),
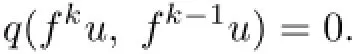
Therefore,
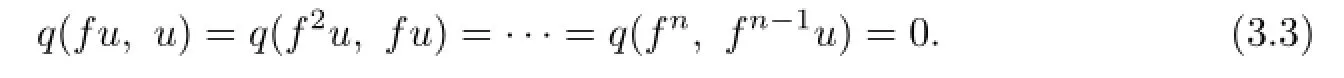
Similarly,we have
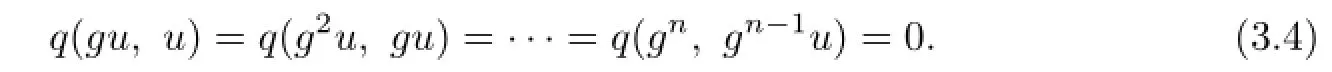
By(3.3),for any k=1,2,···,n,we have
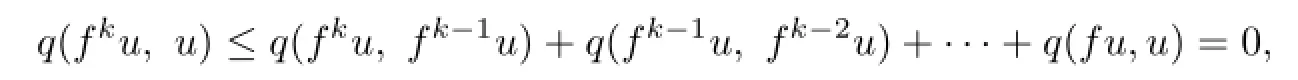
hence
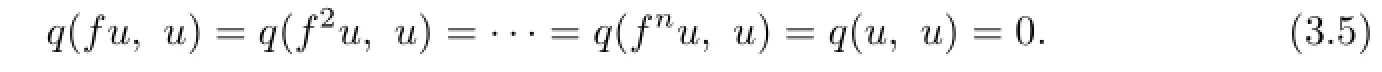
Similarly,by(3.4),we have

By using(3.1)and(3.6),we obtain
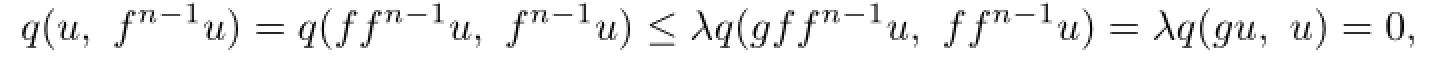
i.e.,
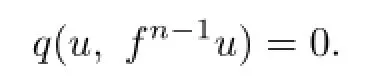
Hence
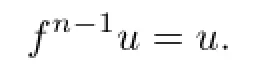
Similarly,
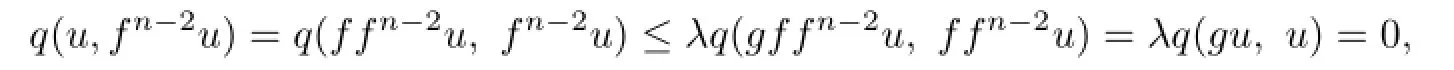
i.e.,
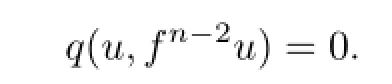
Hence fn−2u=u.
Repeating this process,we obtain
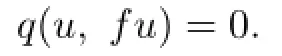
Hence fu=u.
Similarly,by(3.2)and(3.5),gu=u.Hence u∈F(f)∩F(g).Thereby
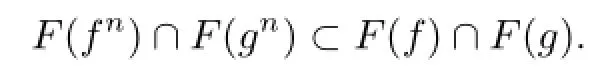
So
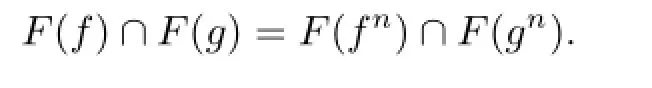
Theorem 3.2Let(X,d)be a complete TVS-valued cone metric space,q be a c-distance. Suppose that a onto and continuous mapping f:X→X satisfies
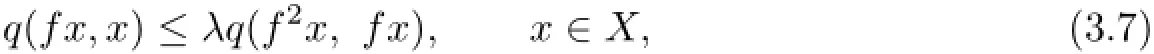
where λ∈(0,1).Then f has a fixed point u∈X with q(u,u)=0 and P-property.
Proof.Let f=g in Theorem 3.1.Then(3.1)and(3.2)deduce to(3.7).
Example 3.1Let E=C1R[0,1]and define a norm on E as
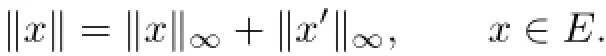
Let P0={x∈E:x≥0}.Then E is a Banach space with a non-normal cone P(see[20] and[21]).
Let X=[0,∞)and define d:X×X→E as

Then(X,d)is a TVS-valued cone metric space with a non-normal cone P0.
Define q:X×X→E as
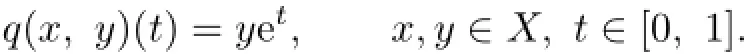
Then it is easy to know that q is a c-distance on X by Example 2.14 in[22].
Let f:X→X,fx=2x for all x∈X and take.Then,for any x∈X,
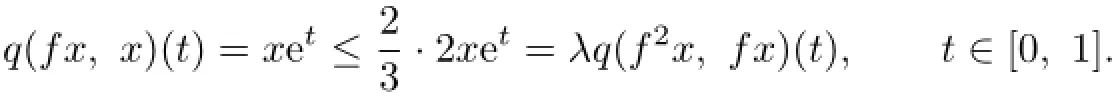
Hence
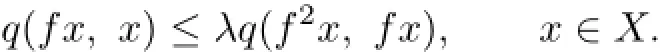
So f and λ satisfy all conditions of Theorem 3.2,therefore f has a fixed point 0.Obviously,q(0,0)=0 and f has P-property.
Remark 3.1The condition(3.7)in Theorem 3.2 is equivalent to the following condition
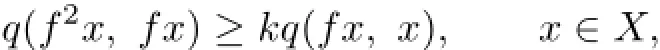
where k>1.Hence Theorem 3.2 is a new fixed point theorem for a generalized I-expansive mapping(see[23])under c-distance on TVS-valued metric spaces.
References
[1]Huang L G,Zhang X.Cone metric spaces and fixed point theorems of contractive mappings. J.Math.Anal.Appl.,2007,332(2):1468–1476.
[2]Du W S.A note on cone metric fixed point theory and its equivalence.Nonlinear Anal.,2010,72:2259–2261.
[3]Kadelburg Z,Radenovi´c S,Rako˘cevi´c V.Topological vector space valued cone metric spaces and fixed point theorems.Fixed Point Theory Appl.,2010,2010(1):1–17.
[4]Abdeljawad Th,Karapinar E.A gap in the paper“A note on cone metric fixed point theory and its equivalence,Nonlinear Anal.2010,72:2259–2261”.Gazi Univ.J.Sci.2011,24(2): 233–234.
[5]Abdeljawad Th,Karapinar E.A common fixed point theorem of Gregus type on convex cone metric spaces.J.Comput.Anal.Appl.,2011,13(4):609–621.
[6]Arandjelovi´c I D,Ke˘cki´c D J.On nonlinear quasi-contractions on TVS-valued cone metric spaces.Appl.Math.Lett.,2011,24:1209–1213.
[7]Karapinar E,Yuksel U.On common fixed theorem without commuting conditions in TVS-cone metric spaces.J.Comput.Anal.Appl.,2011,13:1123–1131.
[8]Simi´c S S.A note on Stone’s,Baire’s,Ky Fan’s and Dugundji’s theorems in TVS-cone metric spaces.Appl.Math.Lett.2011,24:999–1002.
[9]Jankovi´c S,Kadelburg Z,Radenovi´c S.On cone metric spaces,a survey.Nonlinear Asnal.,2011,74:2591–2601.
[10]Piao Y J,Jin H L,Jin Y F.Unique common fixed points for mappings on TVS-valued cone metric spaces.Acta Math.Sci.,2015,35A(1):172–181.
[11]Kada O,Suzuki T,Takahashi W.Nonconvex minimization theorems and fixed point theorems in complete metric spaces.Math.Japonica.,1996,44:381–391.
[12]Abbas M,Ili´c D,Ali Khan M.Coupled coincidence point and coupled common fixed point theorems in partially ordered metric spaces with w-distance.Fixed Point Theory Appl.,2010,2010(1):395–400.
[13]Ili´c D,Rako˘cevi´c V.Common fixed point for maps with w-distance.Appl.Math.Comput.,2008,199:599–610.
[14]Razani A,Nezhad Z M,Boujary M.A fixed point theorem for w-distance.Appl.Sci.,2009,11:114–117.
[15]Chp Y J,Saadati R,Wang S H.Common fixed point theorems on generalized distance in ordered cone metric spaces.Comput.Math.Appl.,2011,61:1254–1260.
[16]Lakzian H,Arabyani F.Some fixed point theorems in cone metric spaces with w-distance. Inter.J.Math.Anal.,2009,22(3):1081–1086.
[17]Wang S H,Guo B H.Distance in cone metric spaces and common fixed point theorems.Appl. Math.Lett.,2011,24:1735–1739.
[18]Djordjevi´c M,Dori´c D,Kadelburg Z,et al.Fixed point results under c-distance in TVS-cone metric spaces.Fixed Point Theory Appl.,2011,2011(1):1–9.
[19]Piao Y J.Fixed point theorems for III,s-III type expansive mappings on CMTS.J.Systems Sci.Math.Sci.,2013,33(8):976–984.
[20]Xu S Y,Radenovi´c S.Fixed point theorems of generalized Lipschitz mappings on cone metric spaces over Banach algebras without assumption of normality.Fixed Point Theory Appl..2014,2014(1):1–12.
[21]Rezapour S,Hamlbarani R.Some note on the paper“Cone metric spaces and fixed point theorems of contractive mappings”.J.Math.Anal.Appl.,2008,345:719–724.
[22]Cho Y J,Saadati R,Wang S.Common fixed point theorems on generalized distance in ordered cone metric spaces.Comput.Math.Appl.,2011,61:1254–1260.
[23]Wang S Z,Li B Y,Gao Z M.Expansive mappings and fixed point theorems.Adv.Math. (China).1982,11(2):149–153.
10.13447/j.1674-5647.2016.03.05
date:July 2,2015.
The NSF(11361064)of China.
E-mail address:sxpyj@ybu.edu.cn(Piao Y J).
 Communications in Mathematical Research2016年3期
Communications in Mathematical Research2016年3期
- Communications in Mathematical Research的其它文章
- Extended tanh-function Method for Solving Traveling Wave Solutions of Nonlinear Kundu Equation
- Existence of Multiple Positive Periodic Solutions for Second Order Differential Equations
- On Skew Triangular Matrix Rings
- Existence and Uniqueness of Positive Solutions for a System of Multi-order Fractional Differential Equations
- A Class of Ruin Probability Model with Dependent Structure
- Stochastic Maximum Principle for Optimal Control of Forward-backward Stochastic Pantograph Systems with Regime Switching
