Existence of Multiple Positive Periodic Solutions for Second Order Differential Equations
LYue,Sun Peng,Cai Huaand Han Pei-shan
(School of Mathematics,Jilin University,Changchun,130012)
Communicated by Li Yong
Existence of Multiple Positive Periodic Solutions for Second Order Differential Equations
(School of Mathematics,Jilin University,Changchun,130012)
Communicated by Li Yong
In this paper,we study the existence of multiple positive periodic solutions for the second order differential equation
positive periodic solution,multiplicity,differential equation,Krasnoselskii fixed point theorem
2010 MR subject classification:35J30,35J35
Document code:A
Article ID:1674-5647(2016)03-0272-09
1 Introduction
This paper is concerned with the existence and multiplicity of positive solutions for the following second order differential equation

where p(t),q(t)∈C(R,R+)are ω-periodic,f=(f1,f2,···,fn)T,f(t,x(t))is a functional defined on R×BC and f(t,x(t))is ω-periodic in t,BC denotes the Banach space of bounded continuous functions ϕ:R→Rnwith the normwhere ϕ=(ϕ1,ϕ2,···,ϕn)T.
The existence of positive periodic solutions for differential equations were extensively studied(see[1]–[5]).One of the effective approaches to fulfill such a problem is employing fixed point theorem,and some prior estimations of possible periodic solutions are obtained.Raffoul[6]considered the nonlinear neutral differential equation.Liu and Ge[7]investigated the nonlinear Duffing equation.Jiang et al.[8]considered the existence and nonexistence of positive periodic solutions to a system of infinite delay equation.Recently,many scholars study second order differential equation and obtain some new results(see[9]–[11]).Motivated by the papers mentioned above,we aim to study the existence of multiple positive periodic solutions for the second order differential equation(1.1).
The following definition and theorem are needed in our arguments.
Definition 1.1Let X be a Banach space and E be a closed,nonempty subset of X.E is said to be a cone if
(i)αu+βv∈E for all u,v∈E and all α,β>0;
(ii)u,-u∈E imply u=0.
Theorem 1.1([12],Krasnoselskii fixed point theorem)Let X be a Banach space,and E be a cone in X.Suppose that Ω1and Ω2are open subset of X such that 0∈Ω1⊂¯Ω1⊂Ω2. Suppose that T:E∩(¯Ω2Ω1)→E is a completely continuous operator and satisfies either
(i)∥Tx∥≥∥x∥for any x∈E∩∂Ω1and∥Tx∥≤∥x∥for any x∈E∩∂Ω2;or
(ii)∥Tx∥≤∥x∥for any x∈E∩∂Ω1and∥Tx∥≥∥x∥for any x∈E∩∂Ω2.
Then T has a fixed point in E∩(¯Ω2Ω1).
This paper is organized as follows.In Section 2,we introduce some notations and preliminary results.Section 3 presents some existence results of positive periodic solutions for(1.1).The multiplicity results are given in Section 4.
2 Some Lemmas
In this section,we make some preparations for our main results.
Let X={x∈C(R,Rn);x(t+ω)=x(t),t∈R}with the normObviously,X is a Banach space.
Lemma 2.1[7]Suppose that
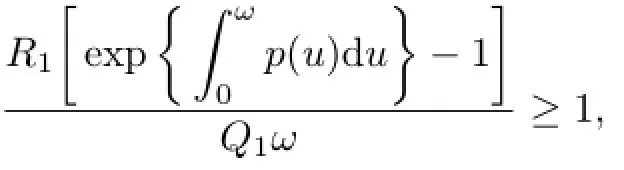
where
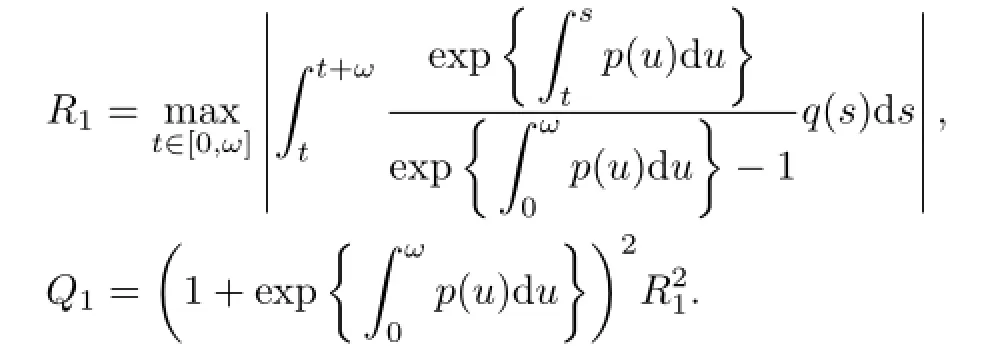
Then there are continuous ω-periodic functions a and b such that
Lemma 2.2Suppose that the conditions of Lemma 2.1 hold.Then the periodic solution of(1.1)can be expressed by

where
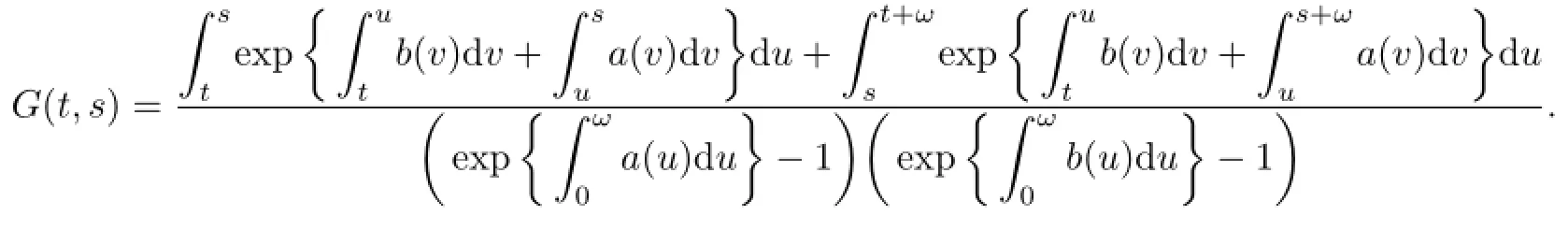
Proof.Let

By a direct calculation we can obtain that
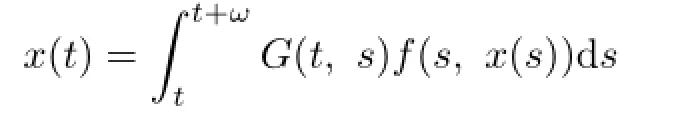
is a ω-periodic solution of(1.1).
Suppose that x(t)is a ω-periodic solution of(1.1).From Lemma 2.1 we have
which is equivalent to

Therefore,
Corollary 2.1Green’s function G(t,s)satisfies the following properties:
G(t,t+ω)=G(t,t),
G(t+ω,s+ω)=G(t,s),
Corollary 2.2Function G(t,s)satisfies
where
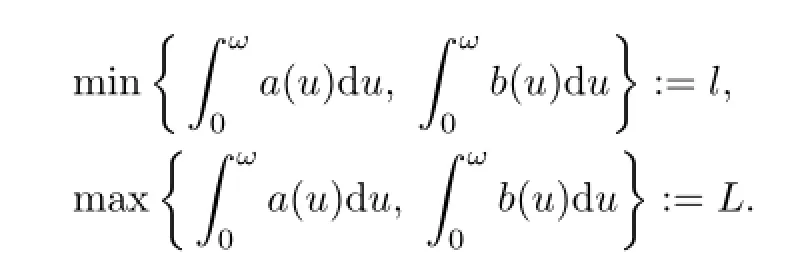
Let
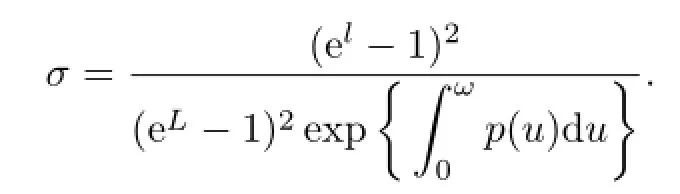
Define
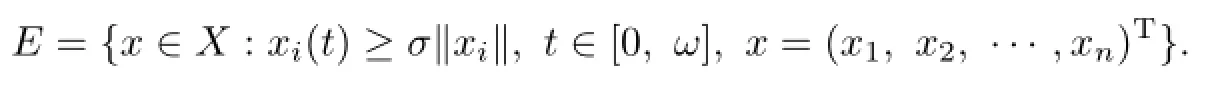
One may verify that E is a cone.
We make the assumptions:
(A1)f(t,x(t))is a continuous function of t for each x∈BC(R,).
(A2)For any L>0 and ϵ>0,there exist δ>0 such that ϕ,ψ∈BC,∥ϕ∥≤L,∥ψ∥≤L,∥ϕ-ψ∥≤δ imply|f(s,ϕ)-f(s,ψ)|<ε.
(A3)For(t,s)∈R2and(u,ϕ)∈BC(R,Rn+),G(t,s)f(u,ϕ)≥0.
Define the mapping H by
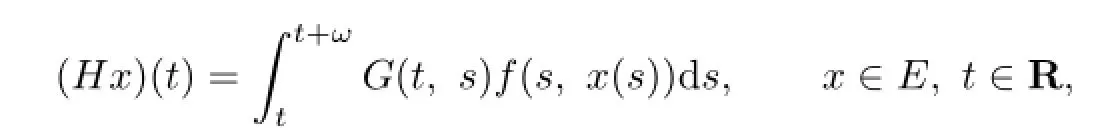
and(Hx)=(H1x,H2x,···,Hnx)T.
Lemma 2.3Suppose that(A1)–(A3)hold.Then H:E→E and H is compact.
Proof.For x∈E,we have

Thus,(Hx)∈X.By Corollary 2.2,for x∈E,we have

and
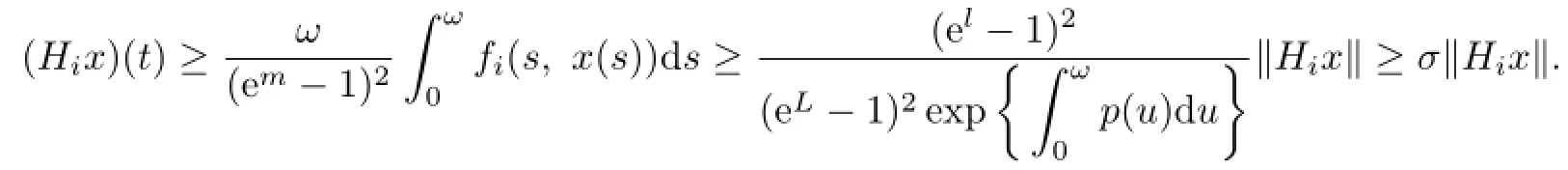
Therefore,(Hx)∈E.By(A2),the proof of the compactness is easily obtained by using the Arzela-Ascoli theorem.
3 Existence of Positive Solutions
In order to state our main results,we assume the following limits exist and let
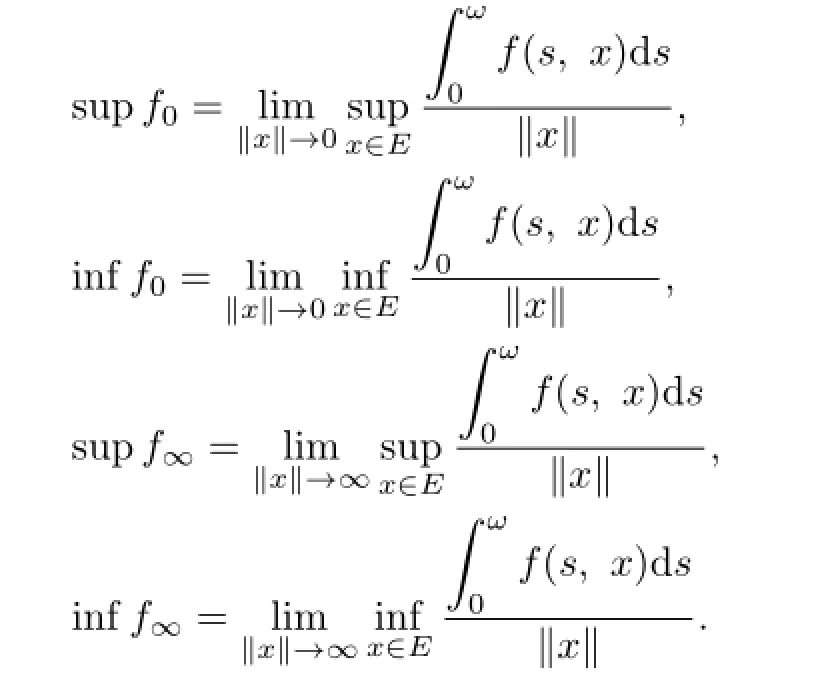
Moreover,we assume that
(P1)inf f0=∞.
(P2)inf f∞=∞.
(P3)supf∞=0.
(P4)supf0=0.
Theorem 3.1If(P1)and(P3)hold,then(1.1)has at least one positive ω-periodic solution.
Proof.By(P1)we can find r0>0 such that
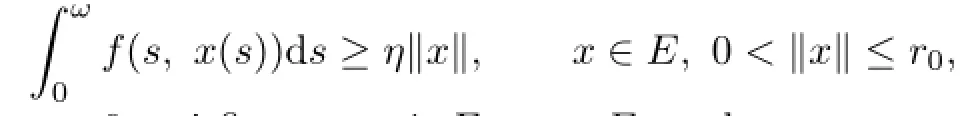
where the constant η>0 satisfies mη>1.For x∈E,we have
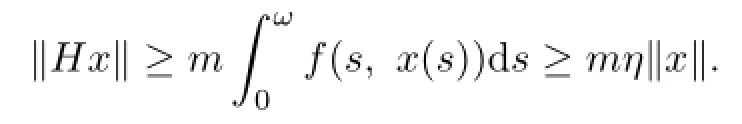

We choose
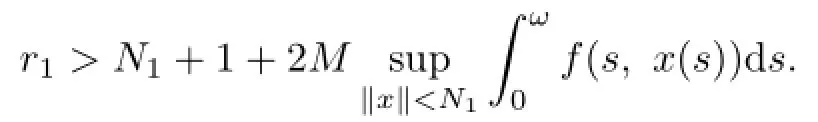
If x∈E∩∂Ωr1,then
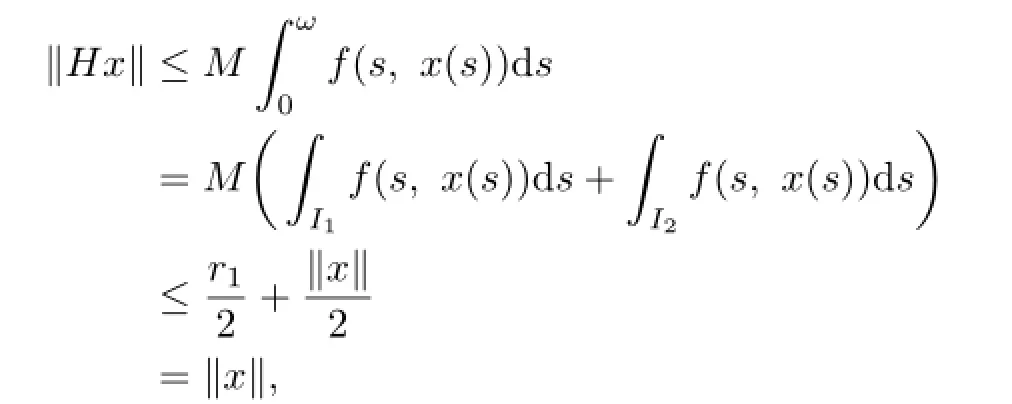
where
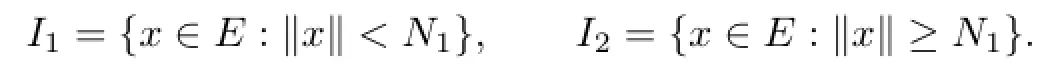
Thus,H satisfies all the requirements in Theorem 1.1.By Theorem 1.1 H has a fixed point in
Theorem 3.2If(P2)and(P4)hold,then(1.1)has at least one positive ω-periodic solution.
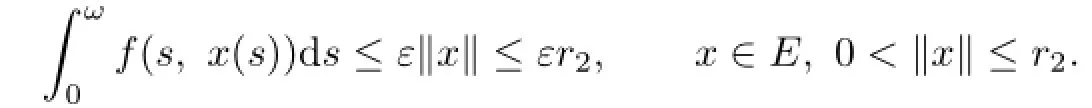
We have

By(P2)there exists an r3>r2>0 such that

It follows from Theorem 1.1 that the equation(1.1)has a positive ω-periodic solution satisfying r2≤∥x∥≤r3.This completes the proof.
In the following,we assume that
(P5)There exists a d1>0 such that
(P6)There exists a d2>0 such that
Theorem 3.3If(P5)and(P6)hold,then(1.1)has at least one positive ω-periodic solution.
Proof.If x∈E∩∂Ωd2,then by(P6)we have
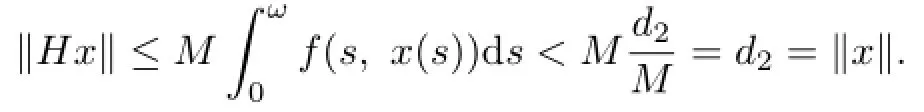
And by(P5)we have
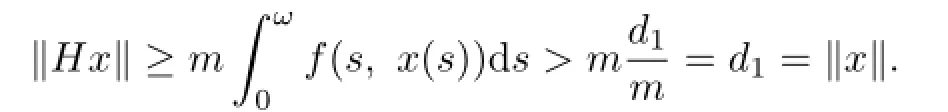
Without loss of generality,we assume that d2<d1.Thus,by Theorem 1.1 we can obtain the conclusion.This completes the proof.
We make the following assumption:
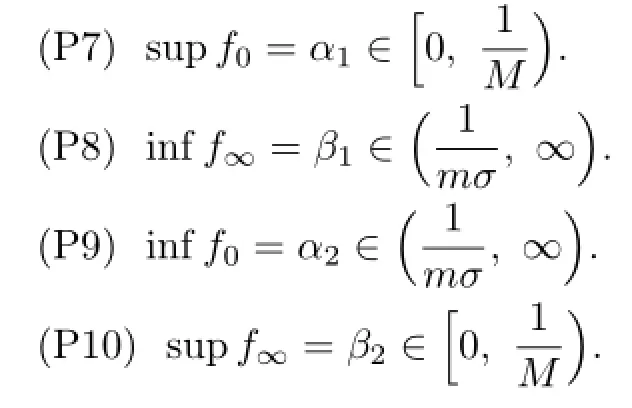
Theorem 3.4If(P7)and(P8)hold,then(1.1)has at least one positive ω-periodic solution.
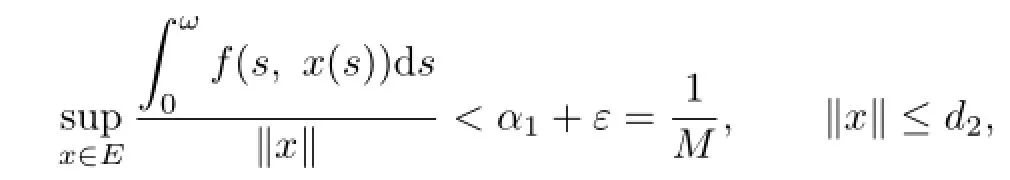
that is,
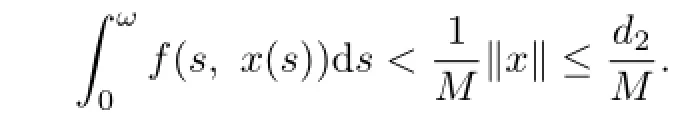
So(P6)is satisfied.

that is,

Therefore,(P5)holds.By Theorem 3.3,we complete the proof.
From the analogous arguments in the above proof,we can obtain the following consequence.
Theorem 3.5If(P9)and(P10)hold,then(1.1)has at least one positive ω-periodic solution.
4 Multiplicity of Positive Solutions
Theorem 4.1If(P3),(P4)and(P5)hold,then(1.1)has at least two positive ω-periodic solutions.
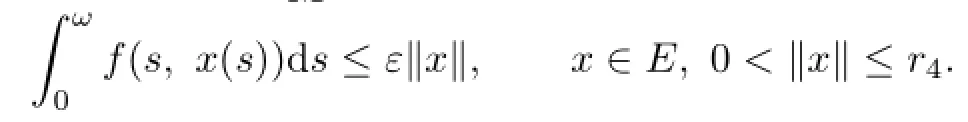
We have
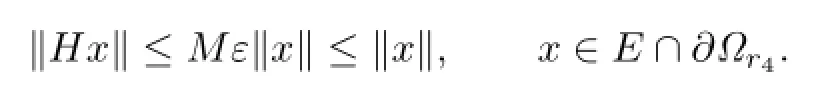
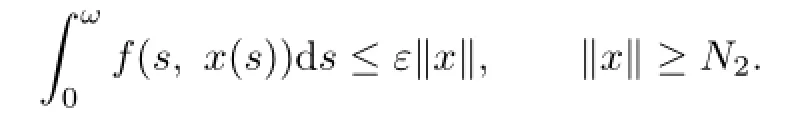
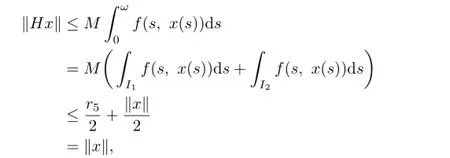
where

So

Let Ωd1={x∈X:∥x∥<d1}.Then,by(P5),for x∈E∩∂Ωd1,we have
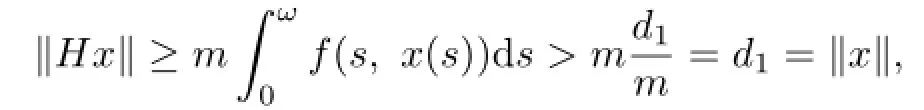
which shows that
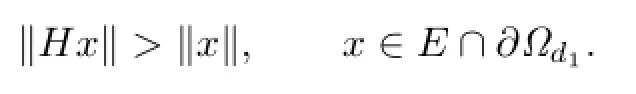
By Theorem 2.1,there exist two positive ω-periodic solutions x1and x2satisfying
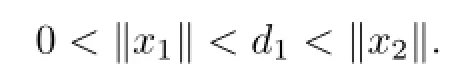
Theorem 4.2If(P6),(P8)and(P9)hold,then(1.1)has at least two positive ω-periodic solutions.
Proof.By(P8)there exists a sufficiently large d1>d2such that
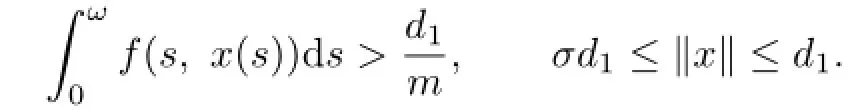
By(P9)there exists a sufficiently small∈(0,d2)such that
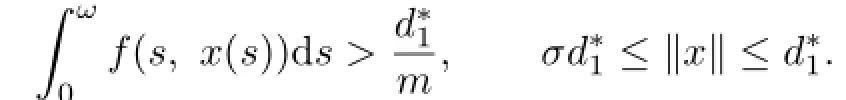
Therefore,we can obtain that there exist two positive solutions x1and x2satisfying
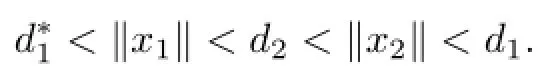
This completes the proof.
From the analogous arguments in the above proof,we can obtain the following consequences.
Theorem 4.3If(P1),(P2)and(P6)hold,then(1.1)has at least two positive ω-periodic solutions.
Theorem 4.4If(P5),(P7)and(P10)hold,then(1.1)has at least two positive ω-periodic solutions.
References
[1]Chow S N.Existence of periodic solutions of autonomous functional equations.J.Differential Equations,1974,15:350–378.
[2]Deimling K.Nonlinear Functional Analysis.New York:Springer-Verlag,1985.
[3]Ma M J,Yu J S.Existence of multiple positive periodic solutions for nonlinear functional difference equations.J.Math.Anal.Appl.,2005,305:483–490.
[4]Wang H Y.Positive periodic solutions of functional differential equations.J.Differential Equations,2004,202:354–366.
[5]Ye D,Fan M,Wang H Y.Periodic solutions for scalar functional differential equations.Electron. J.Differential Equations,2003,102:1–7.
[6]Raffoul Y N.Periodic solutions for neutral nonlinear differential equations with functional delay.Nonlinear Anal.,1996,26:1023–1033.
[7]Liu Y,Ge W.Positive periodic solutions of nonlinear Duffing equations with delay and variable coefficients.Tamsui Oxf.J.Math.Sci.,2004,20:235–255.
[8]Jiang D Q,O’Regan D,Agarwal R P,Xu X J.On the number of positive periodic solutions of functional differential equations and population models.Math.Model Methods Appl.Sci.,2005,15(4):555–573.
[9]Wei Y H.Existence and uniqueness of periodic solutions for second order differential equations. J.Funct.Spaces,2014,2014:Article ID 246258,5pp.
[10]Ma Y.Existence of positive periodic solutions of second order differential equations with weak singularities.Bound.Value Probl.,2014,188:8pp.
[11]Liu J,Feng H Y.Positive solutions of periodic boundary value problems for second order differential equations with the nonlinearity dependent on the derivative.J.Appl.Math.Comput.,2015,49(1-2):343–355.
[12]Krasnosel’ski˘ı M A.Positive solution of operator equation.Translated from the Russian by Richard E.Flaherty;edited by Leo F.Boron Groningen:P.Noordhoff Ltd.1964,381pp.
10.13447/j.1674-5647.2016.03.09
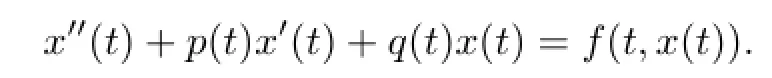
date:March 21,2016.
*Corresponding author.
E-mail address:lvyue@jlu.edu.cn(L¨u Y),caihua@jlu.edu.cn(Cai H).
By using Krasnoselskii fixed point theorem,we establish some criteria for the existence and multiple positive periodic solutions for this differential equation.
 Communications in Mathematical Research2016年3期
Communications in Mathematical Research2016年3期
- Communications in Mathematical Research的其它文章
- Extended tanh-function Method for Solving Traveling Wave Solutions of Nonlinear Kundu Equation
- On Skew Triangular Matrix Rings
- Existence and Uniqueness of Positive Solutions for a System of Multi-order Fractional Differential Equations
- A Class of Ruin Probability Model with Dependent Structure
- Common Fixed Point Theorems and Q-property for Quasi-contractive Mappings under c-distance on TVS-valued Cone Metric Spaces without the Normality
- Stochastic Maximum Principle for Optimal Control of Forward-backward Stochastic Pantograph Systems with Regime Switching
